Свойства биссектрисы треугольника как найти

Свойства биссектрисы треугольника как найти

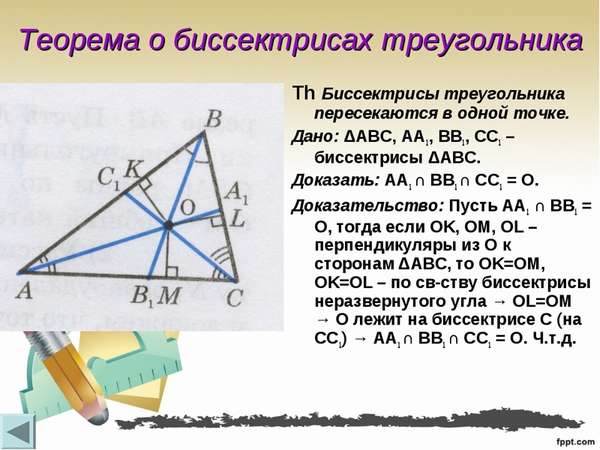
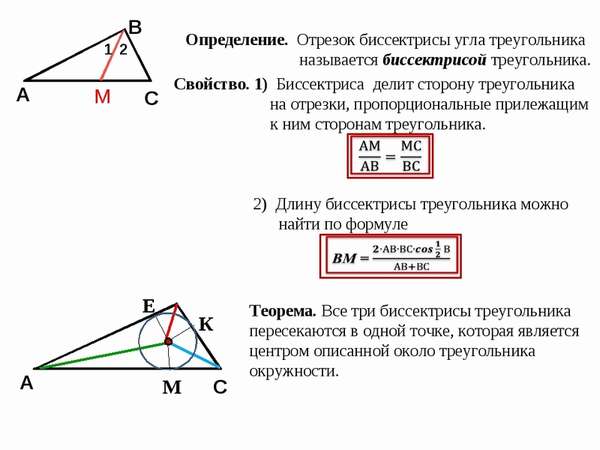
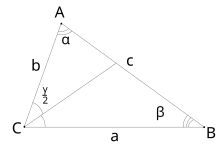
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

  • Определение биссектрисы угла треугольника

  • Свойства биссектрисы треугольника

    • Свойство 1 (теорема о биссектрисе)

    • Свойство 2

    • Свойство 3

    • Свойство 4

    • Свойство 5

  • Пример задачи

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Внутренняя биссектриса треугольника

  • BD – биссектриса угла ABC;
  • α = β.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Внешняя биссектриса треугольника

  • СD – внешняя биссектриса угла, смежного с ∠ACB;
  • α = β.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Теорема о биссектрисе (формула)

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Центр вписанной в треугольник окружности на пересечении биссектрис (инцентр)

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Пересечение биссектрис в треугольнике

Деление биссектрис треугольника в точке пересечения (соотношение)

Деление биссектрис треугольника в точке пересечения (соотношение)

Деление биссектрис треугольника в точке пересечения (соотношение)

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD2 = AB ⋅ BC – AD ⋅ DC

Биссектриса треугольника

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

Перпендикулярность внешней и внутренней биссектрис одного и того же угла треугольника

  • CD – внутренняя биссектриса ∠ACB;
  • CE – биссектриса угла, смежного с ∠ACB;
  • ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Биссектриса прямоугольного треугольника к гипотенузе

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC2 = AB2 + AC2 = 62 + 82 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Теорема о биссектрисе (пример задачи)

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Следовательно, AD ≈ 4,85 см.

Источник

15
Мар 2013

Категория: ВидеоурокиПланиметрияСправочные материалы

Элементы треугольника. Биссектриса

2013-03-15
2015-11-24

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

биссектриса треугольника

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса  угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ( frac{{AB}}{{AC}} = frac{{BD}}{{CD}})

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

l_c = {sqrt{ab(a+b+c)(a+b-c)}over{a+b}} (доказательство формулы – здесь)
l_c = sqrt{ab-a_lb_l}, где
l_c — длина биссектрисы, проведённой к стороне c,
a, b, c — стороны треугольника против вершин A, B, C соответственно,
a_l, b_l — длины отрезков, на которые биссектриса l_c делит сторону c,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Задача на свойства биссектрисы

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Автор: egeMax |

комментария 2
| Метки: биссектриса

Источник

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

  • CD – внутренняя биссектриса ∠ACB;
  • CE – биссектриса угла, смежного с ∠ACB;
  • ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Биссектриса – свойства, признаки и формулы

Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.

Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.

Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.

Что такое биссектриса в геометрии

Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.

Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.

В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.

Биссектриса прямоугольного треугольника

Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).

Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.

В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 90 0 .

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.

Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Все формулы биссектрисы в треугольнике

В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, lc, равна:

Примеры решения задач

Задача №1

В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.

Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.

Тогда OE : OB = 1 : 2по свойству медиан.

Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.

Это означает, что CA : AB = 1 : 2.

Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.

Задача №2

Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.

Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.

По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.

[spoiler title=”источники:”]

Элементы треугольника. Биссектриса

http://nauka.club/matematika/geometriya/bissektrisa.html

[/spoiler]

Источник

Биссептриса треугольникаМатематика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.

Оглавление:

  • Свойства
  • Свойства в равнобедренных треугольниках
  • Определение биссектрисы треугольника
  • Определение длины
  • Нахождение величины угла

Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.

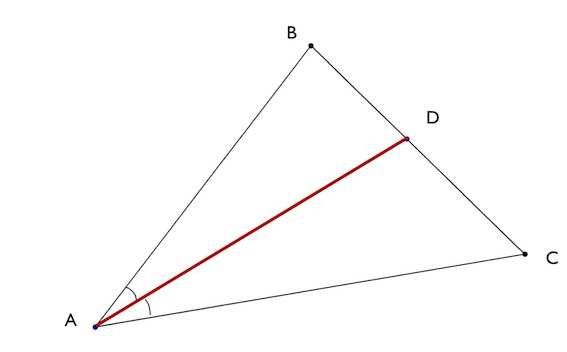
Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.

Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.

Это интересно: Как найти периметр треугольника.

Свойства

  1. Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
  2. Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.

Свойства в равнобедренных треугольниках

  1. Биссектриса прямоугольникаПервое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
  2. Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
  3. Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
  4. Все биссектрисы равностороннего треугольника обладают равенством.

Определение биссектрисы треугольника

Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.

Определение длины

Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

Вычисление длин биссектрисНайдем длину стороны BC.

  • Из свойств известно, что BD/CD = AB/AC.
  • Значит, BD/CD = 5/4 = 1,25.
  • BD/3 = 5/4.
  • Значит, BD = 3,75.
  • ABxAC = 54=20.
  • CDxBD = 33,75 = 11,25.

Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.

Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.

Это интересно: в чем выражается эволюционный характер развития общества?

Нахождение величины угла

Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.

Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.

Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.

Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.

Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Проведите ночь в компании красивой проститутки СПБ . Посетите наш онлайн-портал, и вы обнаружите подборку самых способных девушек своего города. Изучите все доступные варианты, и мы посодействуем вам в выборе подходящей спутницы! Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.

Биссектриса треугольника Как вычислить биссептрисуКак найти биссептрисуЧто такое биссептрисаДлина биссептрисСвойство биссектрисы

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 апреля 2022 года; проверки требуют 32 правки.

Биссектриса AD делит пополам угол A

Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла[1].

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.

(!) Удобно биссектрисы треугольника обозначать следующим образом.

Если ABC ― треугольник, и {displaystyle a=BC}, {displaystyle b=AC}, {displaystyle c=AB} ― длины сторон (или просто стороны), то {displaystyle l_{a}}, {displaystyle l_{b}}, l_{c} ― биссектрисы, проведённые соответственно из вершин A, B, C к сторонам a, b, c.

Связанные определения[править | править код]

  • Точка пересечения биссектрисы угла треугольника с его стороной, не являющейся стороной этого угла, называется основанием биссектрисы.

Свойства[править | править код]

Свойства точек пересечения биссектрис[править | править код]

  • Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности (инцентре).
  • Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
  • Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
  • Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.

Свойства, связанные с углами[править | править код]

  • Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
  • Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
  • Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.

Свойства, связанные с дугами[править | править код]

  • Свойство биссектрисы вписанного угла: биссектриса вписанного угла делит на две равные части дугу, на которую этот угол опирается.
  • То же свойство верно и для биссектрисы центрального угла.

Свойства биссектрис равнобедренного треугольника[править | править код]

  • Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
  • Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
  • В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
  • Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной внутреннему углу стороне — основанию, если треугольник равнобедренный.
  • У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
  • У равностороннего треугольника все три внутренние биссектрисы равны.

Свойства оснований биссектрис[править | править код]

  • Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть {frac {BD}{CD}}={frac {AB}{AC}} или {frac {BD}{AB}}={frac {CD}{AC}}.
  • Теорема о биссектрисе — частный случай теоремы Штейнера.
  • Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
  • Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
  • Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
  • Через точку Фейербаха проходит окружность, проведённая через основания трёх биссектрис.
  • В общем случае не пересекаются в одной точке 3 перпендикуляра к сторонам треугольника, проведённые через основания 3 внутренних его биссектрис, которые лежат на этих сторонах. [4]

Свойства осей биссектрис[править | править код]

  • Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
  • Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.

Свойство проекции одной вершины на биссектрисы двух других вершин[править | править код]

  • Если из двух вершин треугольника провести сразу две пары биссектрис (две внутренние и две внешние), а затем на четыре полученные биссектрисы ортогонально спроектировать третью вершину, тогда полученные четыре точки проекций вершины на биссектрисы будут лежать на одной прямой (коллинеарны)[5]. Эта прямая является средней линией треугольника, параллельной той стороне, концами которой являются упомянутые выше две вершины.

Замечание[править | править код]

  • В утверждении: ” Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис”,- не понятно, о каких конкретно четырёх осях биссектрис идет речь. Видимо, речь идет о каких-то осях биссектрис четырёх треугольников, фигурирующих в теореме Микеля. Возможно, что речь идет об осях внешних биссектрис или антиортовых осях этих треугольниов.

Другие свойства[править | править код]

  • Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
  • Расстояния от сторон угла до любой точки биссектрисы одинаковы.
  • Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно,[6] причём даже при наличии трисектора.[7]
  • Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника[8].
  • Три продолжения трёх биссектрис исходного треугольника, через три их основания до их пересечения в трёх вершинах его треугольника трёх внешних биссектрис оказываются в последнем треугольнике в качестве трёх высот.

Тройки отрезков, параллельных трем бессектрисам треугольника[править | править код]

Тройки отрезков, параллельных трем бессектрисам и одновременно пересекающихся в одной точке[править | править код]

  • Каждый кливер есть отрезок, один конец которого находится в середине стороны треугольника и который параллелен биссектрисе угла, противоположного этой стороне. Три кливера, подобных описанному выше, пересекаются в центре Шпикера.
  • Если проведен отрезок с одним концом в точке касания вписанной окружности треугольника с его стороной в направлении параллельно биссектрисе угла, противоположного этой стороне, а затем для двух других сторон построены аналогичные отрезки, то эти три отрезка пересекаются в одной точке[9].

Тройки отрезков, параллельных трем бессектрисам и одновременно образующих 2 треугольника[править | править код]

  • Во вся­кий треугольник ABC мож­но впи­сать 2 треугольника, 3 сто­ро­ны ко­то­рых па­рал­лель­ны 3 биссектрисам треугольника ABC. Эти треугольники име­ют об­щую окруж­ность типа окружности Эйле­ра, то есть 6 их вершин лежат на 1 окруж­ности.[10]

Длина биссектрис в треугольнике[править | править код]

Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.

{displaystyle l_{c}={{sqrt {ab(a+b+c)(a+b-c)}} over {a+b}}={dfrac {2{sqrt {abp(p-c)}}}{a+b}}}, где p — полупериметр.
l_{c}={sqrt {ab-a_{l}b_{l}}}
l_{c}={frac {2abcos {frac {gamma }{2}}}{a+b}}
{displaystyle l_{c}={dfrac {2a_{l}b_{l}cos {dfrac {gamma }{2}}}{sqrt {a_{l}^{2}+b_{l}^{2}-2a_{l}b_{l}cos {(gamma })}}}}
l_{c}={frac {h_{c}}{cos {frac {alpha -beta }{2}}}}

Для трёх биссектрис углов A, B и C с длинами соответственно {displaystyle l_{a},l_{b},} и l_{c}, справедлива формула[11]

{displaystyle {dfrac {(b+c)^{2}}{bc}}l_{a}^{2}+{dfrac {(c+a)^{2}}{ca}}l_{b}^{2}+{dfrac {(a+b)^{2}}{ab}}l_{c}^{2}=(a+b+c)^{2}},
{displaystyle w_{c}^{2}=a_{w}cdot b_{w}-ab=CE^{2}=BEcdot AE-ab},

где:

  • a,b,c — стороны треугольника против вершин A,B,C соответственно,
  • alpha ,beta ,gamma  — внутренние углы треугольника при вершинах A,B,C соответственно,
  • h_{c} — высота треугольника, опущенная на сторону c.
  • l_{c} — длина внутренней биссектрисы, проведённой к стороне c,
  • a_{l},b_{l} — длины отрезков, на которые внутренняя биссектриса l_{c} делит сторону c,
  • {displaystyle w_{c}} — длина внешней биссектрисы, проведённой из вершины C к продолжению стороны AB.
  • {displaystyle a_{w},b_{w}} — длины отрезков, на которые внешняя биссектриса {displaystyle w_{c}} делит сторону {displaystyle c=AB} и её продолжение до основания самой биссектрисы.
  • Если медиана m, высота h и внутренняя биссектриса t выходят из одной и той же вершины треугольника, около которого описана окружность радиуса R, тогда[12]:p.122,#96
{displaystyle 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).}

Длина частей биссектрис в треугольнике[править | править код]

Уравнения биссектрис[править | править код]

{displaystyle y={frac {a_{1}{sqrt {a_{2}^{2}+1}}pm a_{2}{sqrt {a_{1}^{2}+1}}}{{sqrt {a_{2}^{2}+1}}pm {sqrt {a_{1}^{2}+1}}}},x+{frac {b_{1}{sqrt {a_{2}^{2}+1}}pm b_{2}{sqrt {a_{1}^{2}+1}}}{{sqrt {a_{2}^{2}+1}}pm {sqrt {a_{1}^{2}+1}}}}}

См. также[править | править код]

  • Антибиссектриса
  • Высота (геометрия)
  • Высота треугольника
  • Инцентр
  • Медиана треугольника
  • Симедиана
  • Теорема о биссектрисе
  • Ось внешних биссектрис или антиортовая ось
  • Треугольник
  • Треугольник трёх внешних биссектрис
  • Центроид
  • Чевиана

Примечания[править | править код]

  1. ↑ Иванов А. Б. Биссектриса угла // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1977. — Т. 1: А — Г. — С. 496. — 1152 стб. : ил. — 150 000 экз.
  2. ↑ Kimberling, Clark (1994), Central Points and Central Lines in the Plane of a Triangle, Mathematics Magazine Т. 67 (3): 163–187, DOI 10.2307/2690608.
  3. ↑ v. Nagel, C. H. (1836), Untersuchungen über die wichtigsten zum Dreiecke gehörenden Kreise, Leipzig.
  4. ↑ , . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 105.
  5. ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 6. Глава I, п.8
  6. ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам? Архивная копия от 18 октября 2009 на Wayback Machine. Дистанционный консультационный пункт по математике МЦНМО.
  7. ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор Архивная копия от 26 августа 2015 на Wayback Machine. Дистанционный консультационный пункт по математике МЦНМО.
  8. ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
  9. ↑ Решения заданий первого этапа Всесибирской открытой олимпиады школьников 2015-2016 г. по математике. Задача 10.3, С. 5-6// https://sesc.nsu.ru/upload/iblock/1ad/2015_1_math_s.pdf Архивная копия от 20 сентября 2022 на Wayback Machine
  10. ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 26. Глава I. Упражнения. п.33
  11. ↑ Simons, Stuart. Mathematical Gazette 93, March 2009, 115—116.
  12. ↑ Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
  13. ↑ Уравнение биссектрисы угла между двумя прямыми. Задачи повышенной трудности. Прикладная математика. Дата обращения: 3 декабря 2021. Архивировано 3 декабря 2021 года.

Литература[править | править код]

  • Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — 56 с.
  • Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30-31. — ISBN 5-94057-170-0.
Источник

Добавить комментарий