В данной публикации мы рассмотрим основные свойства высоты в равностороннем (правильном) треугольнике. Также разберем пример решения задачи по этой теме.
Примечание: треугольник называется равносторонним, если все его стороны равны.
-
Свойства высоты в равностороннем треугольнике
- Свойство 1
-
Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Пример задачи
Свойства высоты в равностороннем треугольнике
Свойство 1
Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

- BD – высота, опущенная на сторону AC;
- BD – медиана, которая делит сторону AC пополам, т.е. AD = DC;
- BD – биссектриса угла ABC, т.е. ∠ABD = ∠CBD;
- BD – серединный перпендикуляр, проведенный к AC.
Свойство 2
Все три высоты в равностороннем треугольнике имеют одинаковую длину.

AE = BD = CF
Свойство 3
Высоты в равностороннем треугольнике в ортоцентре (точке пересечения) делятся в отношении 2:1, считая от вершины, из которой они проведены.

- AO = 2OE
- BO = 2OD
- CO = 2OF
Свойство 4
Ортоцентр равностороннего треугольника является центром вписанной и описанной окружностей.

- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r (следует из Свойства 3).
Свойство 5
Высота в равностороннем треугольнике делит его на два равных по площади (равновеликих) прямоугольных треугольника.

S1 = S2
Три высоты в равностороннем треугольнике делят его на 6 равных по площади прямоугольных треугольников.
Свойство 6
Зная длину стороны равностороннего треугольника его высоту можно вычислить по формуле:
![]()
a – сторона треугольника.
Пример задачи
Радиус окружности, описанной вокруг равностороннего треугольника, равняется 7 см. Найдите сторону этого треугольника.
Решение
Как мы знаем из Свойств 3 и 4, радиус описанной окружности составляет 2/3 от высоты равностороннего треугольника (h). Следовательно, h = 7 ∶ 2 ⋅ 3 = 10,5 см.
Теперь остается вычислить длину стороны треугольника (выражение выведено из формулы в Свойстве 6):
![]()
Свойства равностороннего треугольника
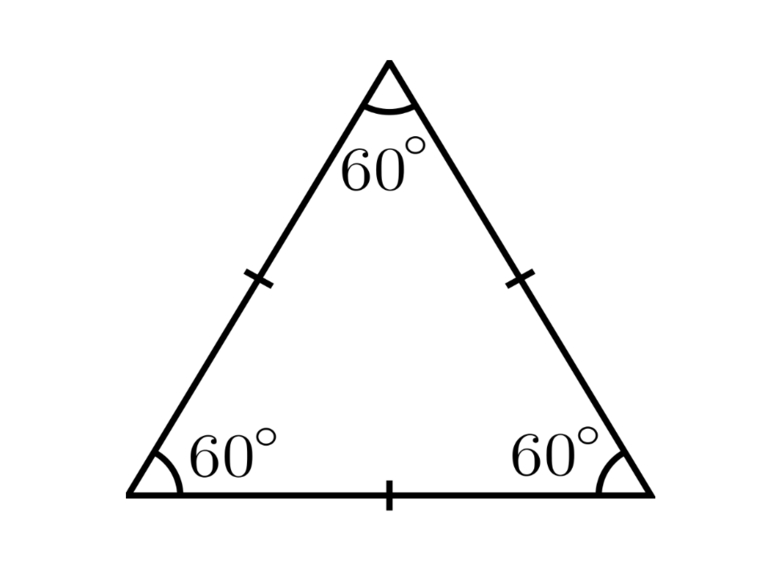
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})
Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка( O) – центр треугольника.
Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).
Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Поэтому (OB=2cdot OK), то есть (R=2cdot r).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.
Давай удостоверимся в этом.

Формулы, используемые для этого, несложны. Вывод выражений основан на свойствах треугольника, при этом точка пересечения высот считается замечательной и даже имеет своё название — ортоцентр.
Общие сведения
Три отрезка, не принадлежащие одной прямой, каждый из которых соединяется с другими в двух точках, образуют геометрическую фигуру — треугольник. Прямые линии — это стороны, а точки их соприкосновения вершины. Один из отрезков, обычно который проходит параллельно горизонтальной плоскости, называют основанием.
В зависимости от размера внутренних углов замкнутой фигуры, треугольники разделяют на следующие виды:
- остроугольные — все углы тела не превышают 90 градусов;
- тупоугольные — один из разворотов имеет тупую форму;
- прямоугольные — размер одного из трёх углов составляет 90 градусов.
По числу равных сторон треугольные фигуры разделяют на разносторонние, равнобедренные, равносторонние. Последние часто называют правильными, так как все стороны у такого объекта равны друг другу. Кроме этого, из особенностей равносторонней фигуры можно отметить, что центры вписанной и описанной окружности совпадают, а каждый из углов равен 60 градусам. Сумма всех углов треугольника равняется 180 градусам.
В любой трёхугольной фигуре можно построить так называемые 3 замечательные линии: медиана, биссектриса и высота.
В правильном треугольнике эти 3 отрезка совпадают, то есть линия, опущенная из вершины к противолежащей стороне, одновременно являясь медианой, биссектрисой и высотой, образует прямой угол с основанием. При этом она делит его пополам. Фактически высота играет роль катета.
Получается, что в середине фигуры можно построить 3 отрезка, которые и будут высотами. Две из них будут опущены на боковые грани, а одна на основание. Точка пересечения перпендикулярных линий называется ортоцентром. Она располагается внутри геометрического тела и совпадает с центром вписанной окружности.
Для трёхугольного тела существует 2 теоремы. Одна из них утверждает, что противолежащие боковые стороны имеют одинаковую длину, а вторая, что если 2 угла невырожденного треугольника равны, то грани, противоположные им, также равны.
Интересно то, что эти правила справедливы как для абсолютной, так и сферической геометрии.
Свойства равносторонней фигуры
При решении задач, связанных с нахождением высоты в равностороннем треугольнике, часто приходится использовать его свойства. Зная их, найти нужные параметры будет несложно. Тем более что все они связаны с главной особенностью фигуры — равенством его всех сторон.
Равностороннее тело с тремя углами обладает следующими особенностями:
- в нём все углы одинаковые и равны 60 градусов;
- середина пересечения отрезков, совпадающих с высотой, биссектрисой и медианой, является центром геометрического тела;
- радиус описанной окружности превышает радиус вписанной в 2 раза;
- в равностороннем треугольнике длины всех элементов выражаются через длину стороны.
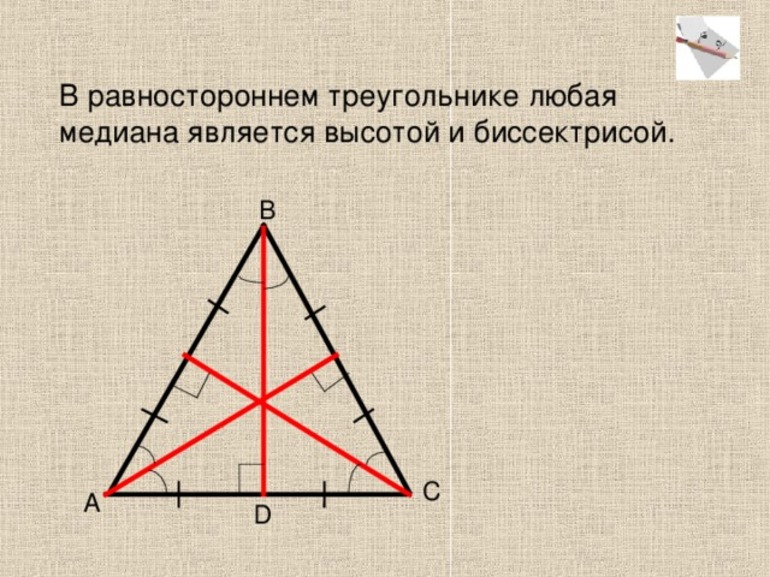
Эти свойства очевидны. Если начертить треугольник с равными сторонами и вписать его в окружность, за центр можно принять точку O, при этом радиус описанного круга будет OK. Тогда линия, проведённая из неё к вершине, будет радиусом. Пусть конечная точка будет B. Но так как место пересечения является общим и для высот и медиан, из свойства последних можно сделать вывод, что в точке линия делится в отношении 2 к 1. Отсчёт следует вести с вершины треугольника. Значит: OB = 2 * OK.
Из основных формул, которые используются при вычислениях, в первую очередь нужно запомнить:
- радиус описанной окружности: R = (a * √3) / 3;
- диаметр вписанного круга: r = (a * √3) / 6;
- медиана: h = (a * √3) / 2;
- площадь: s = (a2 * √3) / 4;
- периметр: p = 3 * a.
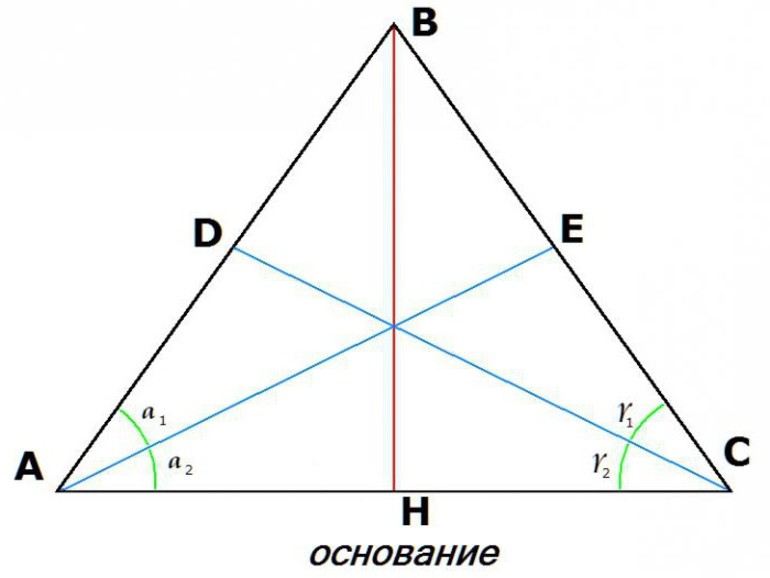
Если рассмотреть треугольник ABC с проведённой высотой BN, можно утверждать, что грань АВ = ВС = АС = AN /2 = NC /2. Так как фигура ABN является копией BNC в зеркальном отражении, разделённые углы у вершины будут одинаковыми, а и их разворот составлять 30 градусов. Из этого следует, что угол A равен 60 градусам, значит, отрезок BN = AB * sin 600 = (AB * √3) / 2.
Зная длину медианы (высоты), вычислить другие параметры треугольника не составит труда. Например, периметр, P = 2 √3 * h; площадь — S = (h * 2) / √3.
При этом замечательным свойством является ещё и то, что ортоцентр одновременно будет в фигуре и центром тяжести (центроидом), поэтому точка пересечения высот и делит отрезок в отношении 2 к 1.
Формула высоты
В равностороннем треугольнике длина стороны равна произведению удвоенной высоты и квадратного корня из трёх. Эту формулу легко доказать, используя теорему Пифагора. Так как высота одновременно является и биссектрисой, она, проведённая на противоположное основание, разделяет треугольник на 2 симметричные фигуры. Исходя из того, что отрезок — это перпендикуляр, полученные геометрические тела будут прямоугольными.
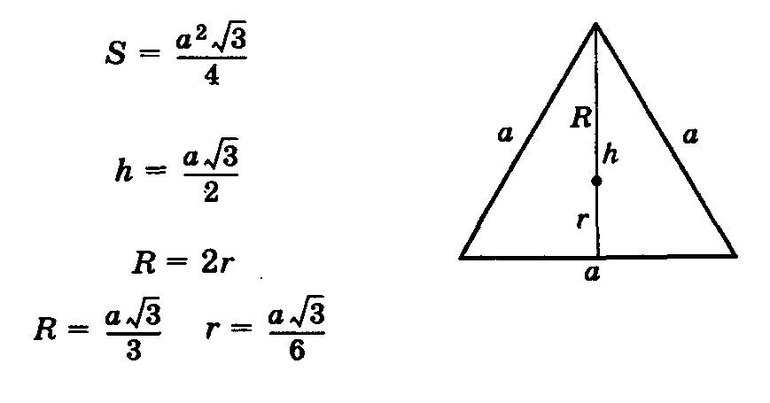
Гипотенуза будет являться гранью основного тела, одним из катетов — проведённая линия, а вторым — половина основания. Последнее утверждение правдиво, так как в равносторонней фигуре все стороны равны. Соответственно, используя теорему Пифагора: c2 = b2 + a2, для рассматриваемого случая можно записать следующую формулу: a2 = h2 + a2 / 22, где: a — грань. После математических преобразований выражение примет вид: a = (2 * h) / √3. Отсюда уже можно вывести формулу для нахождения длины: h = (a * √3) / 2.
Аналогичное определение можно получить, используя для доказательства формулу Герона. Отрезок, являющийся высотой, можно найти из выражения: h = (2 * √p * (p — a) * (p — b) * (p — a)) / b. В равенстве p является периметром и находится как сумма всех сторон: p = (a + b + a). Так как одна из граней делится пополам, формулу можно привести к виду: p = (a + b + a) / 2 = a + b / 2.
После подстановки полученного выражения в формулу Герона, оно примет вид: h = 2 * √((a + b/2) * (b/2) * (a -b/2) * (b/2)) / b. Используя формулу сокращённого умножения: разность квадратов, равенство можно привести к виду: (a + b / 2) * (a — b / 2) = a2 — (b / 2)2.
Для упрощения выражения под корень можно внести двойку и знаменатель b. Таким образом, формула примет вид: h = √(22 * (a2 — (b/2)2 * (b/2)2) * b2). Выполнив ряд сокращений, равенство можно будет представить: h = √(a2 — (b2/4)). Из-за того, что стороны в трёхугольной фигуре совпадают, окончательный вариант можно записать: h = (a√3) / 2. Что и следовало доказать.
Высоту можно определить, и зная радиус вписанной окружности. Её можно найти по формуле: r = (a √ 3) / 6. Если выражение переписать как r = (1 / 3) * ((a √3) / 2), возможно увидеть, что второй множитель как раз и есть высота. Соответственно, r = (1/3) * h. Отсюда: h = 3 * r. Это довольно простая формула, которая часто используется при геометрических вычислениях, поэтому её тоже нужно запомнить.
Решение примеров
Самостоятельное решение задач позволяет закрепить теоретические знания и запомнить формулы. Существуют определённые типы примеров, с помощью которых можно довольно быстро проработать весь изученный материал. Вот некоторые из них, рассчитанные на учеников восьмых классов средней школы:
- Определить высоту равносторонней фигуры, если её грань равняется 6 см. Решение задачи нужно строить следующим образом. У такого треугольника все стороны равны. Так как высота является медианой, она делит противоположную сторону вершины, из которой опущена, на 2 равные части. Треугольник можно обозначить ABC, а искомый перпендикуляр BH. Образованное геометрическое тело является прямоугольным. Причём, согласно условию, у него известна гипотенуза и катет. Оставшийся катет, который и является высотой, легко найти по теореме Пифагора: BH2 + 32 = 62. Отсюда: BH2 = 25. Высота рассматриваемой фигуры будет равна 5 см.
- Сторона правильного треугольного тела равна √3. Узнать, чему будет равен радиус описанной окружности. Эту задачу можно решить, воспользовавшись свойством высоты в равностороннем треугольнике: точка пересечения медиан делит их в отношении 2 :1. Для наглядности можно нарисовать треугольник c вершинами ABC и высоту AK, а точку пересечения обозначить буквой O. Линия AO будет искомым радиусом окружности и составлять 2/3 от всей высоты AK. Длина отрезка равна: AK = √ (AB2 — AK2). Отсюда: R = (2 * √ (AB2 — AK2)) / 3 = (2 * √ (√ 32 — (3/2)2)) / 3 = 1. Задача решена.
Проверить правильность решения можно, используя онлайн-калькуляторы. Это интернет-сервисы, которые позволяют своим пользователям в автоматическом режиме вычислять различные математические примеры. Свои услуги они предоставляют бесплатно, от пользователя требуется только установленный веб-обозреватель и подключение к сети.
Важно ещё, что калькуляторы не только выдают быстро правильный ответ, но и показывают пошаговое решение. Это очень удобно, когда необходимо определить, на каком этапе была допущена ошибка.
Кроме этого, на своих страницах такого рода сервисы содержат краткий теоретический материал и даже примеры заданий. Так что калькуляторы будут полезны и на стадии обучения.
Какими свойствами обладает высота равностороннего треугольника? Как найти высоту равностороннего треугольника через его сторону, радиусы вписанной или описанной окружностей?
Теорема 1
(свойство высоты равностороннего треугольника)
В равностороннем треугольнике высота, проведённая к любой стороне, является также его медианой и биссектрисой.
 Доказательство:
Доказательство:
Пусть в треугольнике ABC AB=BC=AC.
Так как AB=BC, треугольник ABC равнобедренный с основанием AC.
Проведём высоту BF.
 По свойству равнобедренного треугольника, BF является также его медианой и биссектрисой
По свойству равнобедренного треугольника, BF является также его медианой и биссектрисой
(то есть, AF=FC, ∠ABF=∠CBF).
 Аналогично, рассмотрев треугольник ABC как равнобедренный с основанием BC и треугольник ABC — равнобедренный с основанием AB, доказываем, что высоты AK и CD являются также его медианами и биссектрисами
Аналогично, рассмотрев треугольник ABC как равнобедренный с основанием BC и треугольник ABC — равнобедренный с основанием AB, доказываем, что высоты AK и CD являются также его медианами и биссектрисами
(то есть, BK=KC, ∠BAK=∠CAK; AD=BD, ∠ACD=∠BCD).
Что и требовалось доказать.
Теорема 2
(свойство высот равностороннего треугольника)
Все три высоты равностороннего треугольника равны между собой.
Доказательство:

Пусть в треугольнике ABC AB=BC=AC.
AK, BF и CD — его высоты.
В прямоугольных треугольниках ABF, BCD и CAK:
гипотенузы AB, BC и CA равны по условию,
∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника).
 Следовательно, треугольники ABF, BCD и CAK равны (по гипотенузе и острому углу).
Следовательно, треугольники ABF, BCD и CAK равны (по гипотенузе и острому углу).
Из равенства треугольников следует равенство соответствующих сторон: BF=CD=AK.
Что и требовалось доказать.
Из теорем 1 и 2 следует, что в равностороннем треугольнике все высоты, медианы и биссектрисы равны между собой.
1) Найдём высоту равностороннего треугольника через его сторону.

В треугольнике ABC AB=BC=AC=a.
BF — высота, BF=h.
Рассмотрим прямоугольный треугольник ABF.
По определению синуса,
![]()
![]()
Отсюда формула высоты равностороннего треугольника через его сторону:
![]()
(2-й способ: из прямоугольного треугольника ABF по теореме Пифагора
![]()
2) Выразим высоту равностороннего треугольника через радиусы вписанной и описанной окружностей.
Точка O — центр правильного треугольника — является также центром его вписанной и описанной окружностей. Как центр вписанной окружности O — точка пересечения биссектрис треугольника. В правильном треугольнике биссектрисы и медианы совпадают. Следовательно, также является O точкой пересечения медиан.
 А так как медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины, то BO:OF=2:1, то есть
А так как медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины, то BO:OF=2:1, то есть
![]()
![]()
BO — радиус описанной окружности, OF — вписанной: BO=R, OF=r.
Следовательно, высота равностороннего треугольника равна трём радиусам вписанной окружности:
![]()
и в полтора раза больше радиуса описанной окружности:
![]()
![]()
![]()

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Содержание
- 1 Свойства
- 2 Правильный сферический треугольник
- 3 Теоремы о равностороннем треугольнике или содержащие его
- 4 См. также
- 5 Примечания
Свойства[править | править код]

Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
- Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- Периметр правильного треугольника:
- Высоты, медианы и биссектрисы правильного треугольника:
- Площадь правильного треугольника рассчитывается по формулам:
- Радиус описанной окружности равен двойному радиусу вписанной окружности:
- Правильными треугольниками можно замостить плоскость.
- В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
Правильный сферический треугольник[править | править код]
Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.
Теоремы о равностороннем треугольнике или содержащие его[править | править код]
- Задача Наполеона
- Прямая Симсона одно из свойств
- Теорема Вивиани
- Теорема Морли
- Теорема Наполеона
- Теорема Помпею
- Теоремы Тебо 2 и 3
- Точки Аполлония
- Точки Торричелли
См. также[править | править код]
- Замечательные прямые треугольника
- Замечательные точки треугольника
- Равнобедренный треугольник
- Теорема Чевы
- Треугольник
- Треугольник Рёло
Примечания[править | править код]
Символ Шлефли |
|
|---|---|
| Многоугольники |
|
| Звёздчатые многоугольники |
|
| Паркеты на плоскости |
|
| Правильные многогранники и сферические паркеты |
|
| Многогранники Кеплера — Пуансо |
|
| Соты |
{4,3,4} |
| Четырёхмерные многогранники |
|






