Свойство равнобедренного треугольника как найти основание

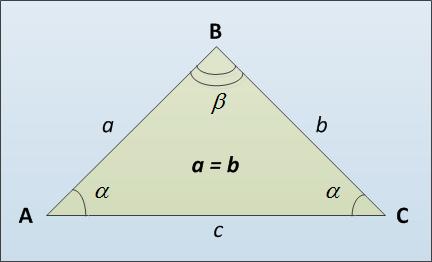
Равнобедренный треугольник – это треугольник, у которого 2 стороны равны. Равные стороны – это рёбра, а 3 сторона – основание. Вариант 1 Если известно, чему равна боковая сторона, а также высота, опущенная на основание. Как известно, высота перпендикулярна основанию, а в случае с равнобедренным треугольником она разбивает его на 2 равных прямоугольных треугольника. Можно по теореме Пифагора найти половину основания, а затем это значение умножить на 2. Вот формула: b = 2√(a² – h²) Вариант 2 Если известно, чему равна боковая сторона и один из углов. Нужно воспользоваться теоремой синусов: a/sinα = b/sinβ = c/sinγ. c = (a*sinγ)/sinα. Так как в равнобедренном треугольнике углы при основании равны, то легко можно найти 2 оставшихся угла, исходя из того, что сумма 3 углов равна 180 градусов. система выбрала этот ответ лучшим Алиса в Стран­е [363K] 5 лет назад  К сожалению у нас нет условия задачи, из которой было бы ясно – на основании каких данных мы должны искать основание нашего равнобедренного треугольника (две стороны боковые которого равны между собой, а основание – это нижняя сторона, которая как раз двум другим не равна). Поэтому рассмотрим несколько вариантов. 1.) Допустим, мы знаем, чему равна боковая сторона и угол треугольника (любой из трех). Тогда мы сначала легко вычисляем два других угла треугольника, помня, что их сумма всегда равна 180 градусам, а затем применяем теорему синусов: следовательно с (основание) будет равно: 2.) Допустим, мы знаем чему равна боковая сторона и высота нашего треугольника. Тогда мы сначала находим половину его основания (она является катетом треугольника, полученного делением исходного равнобедренного треугольника его высотой на два прямоугольных треугольника), применив теорему Пифагора. где с – основание треугольника, которое мы ищем, h – его высота. Марин­а Волог­да [295K] 5 лет назад  Чтобы найти основание равнобедренного треугольника, необходимо вспомнить геометрию. Что такое равнобедренный треугольник – это треугольник, в котором две из трех сторон равны. Теперь вспомним что такое основание треугольника – это как раз третья сторона, которая не равна остальным двум. Так как у нас нет никаких данных задачи, значит следует указать только формулы, по которым можно найти основание. Основание можно найти применив теорему Пифагора по формуле: b = 2√(a² – h²) где h – это высота опущенная на основание; а -сторона треугольника. Чтобы понять, как правильно решать, вот примерная задача: А вот решение для задачи: JuliG­or [3.2K] 9 лет назад  Для того, чтобы найти основание равнобедренного треугольника? нам необходимо знать или один из углов, или же высоту треугольника, которая проводится к его основанию. Основание можно вычислить по следующей, вполне легкой формуле: где b – длина основания треугольника; a – длина стороны треугольника; B – это угол, который противоположен основанию. Alen4­uk [161K] 5 лет назад  Для начала вспомним, какой треугольник называется равнобедренным и из этих его свойств будем уже находить величину основания. Как видим из рисунка, равнобедренный треугольник- это треугольник, у которого две стороны равны и они называются боковыми. Третья же сторона является основанием этого треугольника. Равные стороны называются боковыми. Какие же свойства имеет равнобедренный треугольник, которые помогут нам найти его основание? Углы при основании у равнобедренного треугольника равны между собой. Высота, которую мы опускаем с верхнего угла на основание одновременно является и биссектрисой и медианой. Чтобы найти площадь равнобедренного треугольника нужно разделить на 2 произведение основания на высоту, проведенную к этому основанию. К сожалению, нам не даны условия задачи, поэтому можно использовать несколько формул. Все будет зависеть от данных задачи. Используя эти свойства, мы для нахождения основания можем использовать следующие формулы: Так же нам может помочь в решении теорема синусов. Бекки Шарп [71.2K] 5 лет назад  При решении задач с равнобедренным треугольником нужно использовать свойства как равнобедренного треугольника, так и прямоугольного, поскольку высота равнобедренного треугольника делит его на 2 одинаковых прямоугольных. Основание равнобедренного треугольника ищется, когда есть какие-то исходные данные. Например известны сторона и угол. Тогда поступаем следующим образом: Находим третий угол ( 180 градусов минус сумму двух углов) и используем теорему косинусов: где АС -основание, АВ и ВС – стороны. Рассмотри задачу, когда известны стороны равнобедренного треугольника. Тогда основание ищется, используя теорему Пифагора. Вот здесь нам и понадобится разделить равнобедренный треугольник на два прямоугольных. В итоге основание АС будет равно – 2 квадратных корня из разности квадратов стороны АВ и высоты ВН. 12777­1 [272K] 5 лет назад  Для начала нужно понять, что такое равнобедренный треугольник, таким треугольником называют треугольник у которого две стороны равны. Ниже рисунок такого треугольника: К сожалению нет данных в вопросе. Например, если задана площадь и высота ВH. Тогда основание (на рисунке выше сторона АС) будет равна площадь разделить на высоту BH и умножить на 0,5. Если же нам известна одна сторона и высота треугольника, можно воспользоваться теоремой Пифагора. Ниже представлена формула, по которой можно вычислить основание: b = 2√(a² – h²). Возможно и другие варианты, например, если известна сторона и угол, тогда можно воспользоваться теоремой косинусов или синусов. Nelli­4ka [114K] 5 лет назад  Можно найти для начала значение половины основания, а затем умножить это значение на два. Смысл в том, что мы опускаем на основание из противоположного угла высоту (она в равнобедренном треугольнике совпадает с биссектрисой и медианой), получается два прямоугольных треугольника. Вспоминаем теорему Пифагора, вычисляем разницу между гипотенузой и высотой, извлекаем корень. Конечно, в этом случае по условиям задачи нам должно быть известно значение высоты. Если же известно значение боковой стороны и противоположного основанию угла, то легче всего пойти через формулу синусов: Также можно воспользоваться формулой косинусов: Барха­тные лапки [382K] 5 лет назад  Равнобедренный треугольник – это треугольник у которого две стороны одинаковые, они боковыми, а третья сторона – это основание. Чему равняется основание возможно узнать, если у нас есть данные чему равна одна боковая сторона (а вторая боковая будет равняться также) и высота. В этом случае воспользуемся такой формулой: b = 2(a – h). Как уже видно, для этого нам нужно знать значение боковой стороны и высоты (которая в равнобедренном треугольнике будет такая же как медиана и биссектриса). Но также можно решить эту задачку и другим способом, для этого должны знать чему равняется боковая сторона и один из углов. kkkar­atist­tt [7.7K] 5 лет назад  В задачах такого типа всегда даётся вариант, где у вас известен один угол, если вы знаете одну сторону угла равнобедренного треугольника. То вы умножаете значения на два угла и высоту равнобедренного треугольника. Таким образом вы получите чему равно основание этого треугольника. Бисектриса тоже может вам помоч. Знаете ответ?

Как найти длину основания равнобедренного треугольника

Треугольник – это часть плоскости, ограниченная тремя отрезками прямых, имеющими попарно по одному общему концу. Отрезки прямых в данном определении называются сторонами треугольника, а их общие концы – вершинами треугольника. Если две стороны треугольника равны, то его называют равнобедренным.

Инструкция

Основанием треугольника называется третья его сторона AC (см. рисунок), возможно отличная от боковых равных сторон AB и BC. Приведем несколько способов вычисления длины основания равнобедренного треугольника. Во-первых, можно воспользоваться теоремой синусов. Она гласит, что стороны треугольника прямо пропорциональны значению синусов противолежащих углов: a / sin α = c / sin β. Откуда получаем, что c = a * sin β / sin α.

Приведем пример вычисления основания треугольника по теореме синусов. Пусть a = b = 5, α = 30°. Тогда по теореме о сумме углов треугольника β = 180° – 2 * 30° = 120°. с = 5 * sin 120° / sin 30° = 5 * sin 60° / sin 30° = 5 * √3 * 2 / 2 = 5 * √3. Здесь для вычисления значения синуса угла β = 120° мы воспользовались формулой приведения, согласно которой sin (180° – α) = sin α.

Второй способ найти основание треугольника – при помощи теоремы косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла, заключенного между ними. Получаем, что квадрат основания c^2 = a^2 + b^2 – 2 * a * b * cos β. Далее находим длину основании c, извлекая квадратный корень из данного выражения.

Рассмотрим пример. Пусть нам заданы такие же параметры, как в предыдущей задаче (см. пункт 2). a = b = 5, α = 30°. β = 120°. с^2 = 25 + 25 – 2 * 25 * cos 120° = 50 – 50 * (- cos 60°) = 50 + 50 * ½ = 75. В данном вычислении мы также применили формулу приведения для нахождения cos 120°: cos (180° – α) = – cos α. Извлекаем квадратный корень и получаем значение c = 5 * √3.

Рассмотрим частный случай равнобедренного треугольника – прямоугольный равнобедренный треугольник. Тогда по теореме Пифагора мы сразу же находим основание c = √(a^2 + b^2).

Видео по теме

Обратите внимание

При вычислении легко ошибиться в значениях синуса или косинуса угла, или просто в арифметических действиях. Для проверки разультата полезно вычислить длину основания двумя способами.

Полезный совет

При вычислении угла, противолежащего к основанию, будет удобно использовать следующие формулы приведения: sin (180° – α) = sin α; cos (180° – α) = – cos α.

Источники:

• как найти длину стороны в равнобедренном треугольнике
• Медианы, биссектрисы и высоты треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Равнобедренный треугольник. Онлайн калькулятор

Определение равнобедренного треугольника

Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.

Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).

Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.

Существует более общее определение равнобедненого треугольника:

Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.

Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.

Теорема о равнобедренном треугольнике

Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.

Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:

Из ( small AB=AC) и ( small AD=AE ) следует:

Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что

Из (2) и (4) следует, что ( small angle B= angle C. )

Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )

Свойства равнобедренного треугольника

Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.

Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.

Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.

Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:

Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.

Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.

Признаки равнобедренного треугольника

Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.

Признак 1 следует из определения 1.

Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.

Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).

Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )

Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )

Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда

Применим теорему синусов для треугольника ( small AHC ):

Применим теорему синусов для треугольника ( small AHB ):

тогда, из (5), (6), (7) получим:

Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° – angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B< 180° ) второй вариант исключается. Т.е. ( small angle C= angle B ) и по признаку 2 треугольник является равнобедренным.

Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )

Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.

1. Признак равенства равнобедренных треугольников по основанию и боковой стороне

Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.

Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине

Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.

Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.

3. Признак равенства равнобедренных треугольников по основанию и углу при основании

Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.

Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.

Задачи и решения

Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.

Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:

Откуда:

Подставляя значения ( small a ) и ( small h ) в (9), получим:

Боковая сторона ( small c ) равнобедренного треугольника равна:

Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:

Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:

Найдем угол ( small B ) равнобедренного треугольника:

Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:

Тогда угол ( small C ) равнобедренного треугольника равен:

Поскольку сумма всех углов треугольника равна 180°, то имеем:

Площадь треугольника можно вычислить из формулы:

Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим:

Наконец-то Дзен решил выдавать рекомендации и моя лента обогатилась разными задачками. Сегодня небольшой плагиат с другого канала, где предлагалось решить вот такую задачку:

По условию известна боковая сторона равнобедренного треугольника и медиана проведенная к боковой стороне. Авторское решение заключалось в “удвоении медианы” и применении свойства диагоналей параллелограмма. В комментариях предлагают еще решение через теорему косинусов. Но геометрия как раз и интересна тем, что одну задачу можно решить множеством способов. Поэтому предлагаю решение через свойство медиан треугольника и теорему Пифагора.

Выполним небольшое дополнительное построение.

Т.к. медианы точкой пересечения делятся в отношении 2:1 легко найдем гипотенузу ОМ треугольника АОМ:

Система легко решается методом сложения. Расписываю очень подробно:

Из второго уравнения системы осталось найти х:

За х приняли АМ, значит АС=2АМ (ВМ- медиана)

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 апреля 2023 года; проверки требуют 7 правок.

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно^[1].

Терминология[править | править код]

Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании^[1].

Евклид определил равнобедренный треугольник как треугольник, который имеет две равные стороны, но современная трактовка^[2] предпочитает определение, где треугольник имеет хотя бы две равные стороны, определяя таким образом равносторонний треугольник как частный случай равнобедренного.

Симметрия[править | править код]

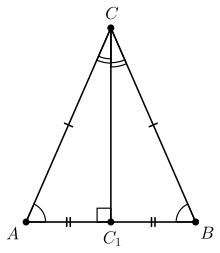
Треугольник с двумя равными сторонами имеет одну ось симметрии, которая проходит через вершинный угол и середину основания. Эта ось симметрии совпадает с биссектрисой вершинного угла, медианой, проведённой к основанию, высотой, проведённой из вершинного угла и с серединным перпендикуляром^{[3][уточнить]}.

Свойства[править | править код]

Основной источник: ^[1]

В равнобедренном треугольнике углы при основании равны. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.

Пусть a — длина равных боковых сторон, b — длина основания, h — высота к основанию, R — радиус описанной окружности

Радиус вписанной окружности может быть выражен пятью способами в зависимости от того, какие два параметра равнобедренного треугольника известны:

• 
• 
• 
• 
• 

Углы могут быть выражены следующими способами:

Периметр равнобедренного треугольника находится следующими способами:

Площадь треугольника находится следующими способами:

Теорема Лемуса-Штейнера[править | править код]

Основной источник: ^[4]

Если две биссектрисы треугольника равны, то этот треугольник — равнобедренный.

Лемус, Штейнер, XIX в.

Доказан этот признак равнобедренного треугольника был только в XIX веке двумя математиками, Лемусом и Штейнером, которые обменивались письмами в течение нескольких лет.

См. также[править | править код]

• Теорема о равнобедренном треугольнике
• Равнобедренный прямоугольный треугольник

Примечания[править | править код]

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — 25-е изд. — М.: Наука, 1978. — 336 с.
  • Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 с.