Таблица брадиса как найти корень

Таблица брадиса как найти корень

Таблица Брадиса – КВАДРАТНЫЕ КОРНИ

Страница 1 из 2

Квадратные корни (Таблица Брадиса 4)

Таблица Брадиса 4 служит для извлечения квадратного корня из любого четырёхзначного числа. Она содержит квадратные корни из всех трёхзначных чисел, заключённых между 1 и 100, вычисленные с 4 значащими цифрами, причём расположение таблицы одинаково с расположением предшествующей таблицы. На 4-ю цифру подкоренного числа, если она есть, берётся поправка.

При перенесении запятой в числе N на 2, 4, 6,… мест запятая в числе “корень из N” переносится в ту же сторону на 1, 2, 3,.., места.

N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
1,0 1,000 1,005 1,010 1,015 1,020 1,025 1,030 1,034 1,039 1,044 0 1 1 2 2 3 3 4 4
1,1 1,049 1,054 1,058 1,063 1,068 1,072 1,077 1,082 1,086 1,091 0 1 1 2 2 3 3 4 4
1,2 1,095 1,100 1,105 1,109 1,114 1,118 1,122 1,127 1,131 1,136 0 1 1 2 2 3 3 4 4
1,3 1,140 1,145 1,149 1,153 1,158 1,162 1,166 1,170 1,175 1,179 0 1 1 2 2 3 3 3 4
1,4 1,183 1,187 1,192 1,196 1,200 1,204 1,208 1,212 1,217 1,221 0 1 1 2 2 2 3 3 4
                    
1,5 1,225 1,229 1,233 1,237 1,241 1,245 1,245 1,253 1,257 1,261 0 1 1 2 2 2 3 3 4
1,6 1,265 1,269 1,273 1,277 1,281 1,285 1,288 1,292 1,296 1,300 0 1 1 2 2 2 3 3 3
1,7 1,304 1,303 1,311 1,315 1,319 1,323 1,327 1,330 1,334 1,338 0 1 1 2 2 2 3 3 3
1,8 1,342 1,345 1,34? 1,353 1,356 1.3g0 1,364 1,367 1,371 1,375 0 1 1 1 2 2 3 3 3
1,9 1,378 1,382 1,386 1,389 1,393 1,396 1,400 1,404 1,407 1,411 0 1 1 1 2 2 3 3 3
                    
2,0 1,414 1,418 1,421 1,425 1,428 1,432 1,435 1,439 1,442 1,446 0 1 1 1 2 2 2 3 3
2,1 1,449 1,453 1,456 1,459 1,463 1,466 1,470 1,473 1,476 1,480 0 1 1 1 2 2 2 3 3
2,2 1,483 1,487 1,490 1,493 1,497 1,500 1,503 1,507 1,510 1,513 0 1 1 1 2 2 2 3 3
2,3 1,517 1,520 1,523 1,526 1,530 1,533 1,536 1,539 1,543 1,546 0 1 1 1 2 2 2 3 3
2,4 1,549 1,552 1,556 1,559 1,562 1,565 1,568 1,572 1,575 1,578 0 1 1 1 2 2 2 3 3
                    
2,5 1,581 1,584 1,587 1,591 1,594 1,597 1,600 1,603 1,606 1,609 0 1 1 1 2 2 2 3 3
2,6 1,612 1,616 1,619 1,622 1,625 1,628 1,631 1,634 1,637 1,640 0 1 1 1 2 2 2 2 3
2,7 1,643 1,646 1,649 1,652 1,655 1,658 1,661 1,664 1,667 1,670 0 1 1 1 2 2 2 2 3
2,8 1,673 1,676 1,679 1,682 1,685 1,688 1,691 1,694 1,697 1,700 0 1 1 1 1 2 2 2 3
2,9 1,703 1,706 1,709 1,712 1,715 1,718 1,720 1,723 1,726 1,729 0 1 1 1 1 2 2 2 3
                    
3,0 1,732 1,735 1,738 1,741 1,744 1,746 1,749 1,752 1,755 1,758 0 1 1 1 1 2 2 2 3
3,1 1,761 1,764 1,766 1,769 1,772 1,775 1,778 1,780 1,783 1,786 0 1 1 1 1 2 2 2 3
3,2 1,789 1,792 1,794 1,797 1,800 1,803 1,806 1,808 1,811 1,814 0 1 1 1 1 2 2 2 2
3,3 1,817 1,819 1,822 1,825 1,828 1,830 1,833 1,836 1,838 1,841 0 1 1 1 1 2 2 2 2
3,4 1,844 1,847 1,849 1,852 1,855 1,857 1,860 1,863 1,865 1,868 0 1 1 1 1 2 2 2 2
                    
3,5 1,871 1,873 1,876 1,879 1,881 1,884 1,887 1,889 1,892 1,895 0 1 1 1 1 2 2 2 2
3,6 1,897 1,900 1,903 1,905 1,908 1,910 1,913 1,916 1,918 1,921 0 1 1 1 1 2 2 2 2
3,7 1,924 1,926 1,929 1,931 1,934 1,936 1,939 1,942 1,944 1,947 0 1 1 1 1 2 2 2 2
3,8 1,949 1,952 1,954 1,957 1,960 1,962 1,965 1,967 1,970 1,972 0 1 1 1 1 2 2 2 2
3,9 1,975 1,977 1,980 1,982 1,985 1,987 1,990 1,992 1,995 1,997 0 1 1 1 1 2 2 2 2
                    
4,0 2,000 2,002 2,005 2,007 2,010 2,012 2,015 2,017 2,020 2,022 0 0 1 1 1 1 2 2 2
4,1 2,025 2,027 2,030 2,032 2,035 2,037 2,040 2,042 2,045 2,047 0 0 1 1 1 1 2 2 2
4,2 2,049 2,052 2,054 2.057 2,059 2,062 2,064 2,066 2,069 2,071 0 0 1 1 1 1 2 2 2
4,3 2,074 2,076 2,078 2,081 2,083 2,086 2,088 2,090 2,093 2,095 0 0 1 1 1 1 2 2 2
4,4 2,098 2,100 2,102 2,105 2,107 2,110 2,112 2,114 2,117 2,119 0 0 1 1 1 1 2 2 2
                    
4,5 2,121 2,124 2,126 2,128 2,131 2,133 2,135 2,138 2,140 2,142 0 0 1 1 1 1 2 2 2
4,6 2,145 2,147 2,149 2,152 2.154 2,156 2,159 2.161 2,163 2,166 0 0 1 1 1 1 2 2 2
4,7 2,168 2,170 2,173 2,175 2,177 2,179 2,182 2,184 2,186 2,189 0 0 1 1 1 1 2 2 2
4,8 2,191 2,193 2,195 2,198 2,200 2,202 2,205 2,207 2,209 2,211 0 0 1 1 1 1 2 2 2
4,9 2,214 2,216 2,218 2,220 2,223 2,225 2,227 2,229 2,232 2,234 0 0 1 1 1 1 2 2 2
N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9

При перенесении запятой в числе N на 2, 4, 6,… мест запятая в числе “корень из N” переносится в ту же сторону на 1, 2, 3,.., места. 

N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
5,0 2,236 2,238 2,241 2,243 2,245 2,247 2,249 2,252 2,254 2,256 0 0 1 1 1 1 2 2 2
5,1 2,258 2,261 2,263 2,265 2,267 2,269 2,272 2,274 2,276 2,278 0 0 1 1 1 1 2 2 2
5,2 2,280 2,283 2,285 2,287 2,289 2,291 2,293 2,296 2,298 2,300 0 0 1 1 1 1 2 2 2
5,3 2,302 2,304 2,307 2,309 2,311 2,313 2,315 2,317 2,319 2,322 0 0 1 1 1 1 2 2 2
5,4 2,324 2,326 2,328 2,330 2,332 2,335 2,337 2,339 2,341 2,343 0 0 1 1 1 1 1 2 2
                    
5,5 2,345 2,347 2,349 2,352 2,354 2,356 2,358 2,360 2,362 2,364 0 0 1 1 1 1 1 2 2
5,6 2,366 2,369 2,371 2,373 2,375 2,377 2,379 2,381 2,383 2,385 0 0 1 1 1 1 1 2 2
5,7 2,387 2,390 2,392 2,394 2,396 2,398 2,400 2,402 2,404 2,406 0 0 1 1 1 1 1 2 2
5,8 2,408 2,410 2,412 2,415 2,417 2,419 2,421 2,423 2,425 2,427 0 0 1 1 1 1 1 2 2
5,9 2,429 2,431 2,433 2,435 2,437 2,439 2,441 2,443 2,445 2,447 0 0 1 1 1 1 1 2 2
                    
6,0 2,449 2,452 2,454 2,456 2,458 2,460 2,462 2,464 2,466 2,468 0 0 1 1 1 1 1 2 2
6,1 2,470 2,472 2,474 2-,476 2,478 2,480 2,482 2,484 2,486 2,488 0 0 1 1 1 1 1 2 2
6,2 2,490 2,492 2,494 2,496 2,498 2,500 2,502 2,504 2,506 2,508 0 0 1 1 1 1 1 2 2
6,3 2,510 2,512 2,514 2,516 2,518 2,520 2,522 2,524 2,526 2,528 0 0 1 1 1 1 1 2 2
6,4 2,530 2,532 2,534 2,536 2,538 2,540 2,542 2,544 2,546 2,548 0 0 1 1 1 1 1 2 2
                    
6,5 2,550 2,551 2,553 2,555 2,557 2,559 2,561 2,563 2,565 2,567 0 0 1 1 1 1 1 2 2
6,6 2,569 2,571 2,573 2,575 2,577 2,579 2,581 2,583 2,585 2,587 0 0 1 1 1 1 1 2 2
6,7 2,588 2,590 2,592 2,594 2,596 2,598 2,600 2,602 2,604 2,606 0 0 1 1 1 1 1 2 2
6,8 2,608 2,610 2,612 2,613 2,615 2,617 2,619 2,621 2,623 2,625 0 0 1 1 1 1 1 2 2
6,9 2,627 2,629 2,631 2,632 2,634 2,636 2,638 2,640 2,642 2,644 0 0 1 1 1 1 1 2 2
                    
7,0 2,646 2,648 2,650 2,651 2,653 2,655 2,657 2,659 2,661 2,663 0 0 1 1 1 1 1 2 2
7,1 2,665 2,666 2,668 2,670 2,672 2,674 2,676 2,678 2,680 2,681 0 0 1 1 1 1 1 1 2
7,2 2,683 2,685 2,687 2,689 2,691 2,693 2,694 2,696 2,698 2,700 0 0 1 1 1 1 1 1 2
7,3 2,702 2,704 2,706 2,707 2,709 2,711 2,713 2,715 2,717 2,718 0 0 1 1 1 1 1 1 2
7,4 2,720 2,722 2,724 2,726 2,728 2,729 2,731 2,733 2,735 2,737 0 0 1 1 1 1 1 1 2
                    
7,5 2,739 2,740 2,742 2,744 2,746 2,748 2,750 2,751 2,753 2,755 0 0 1 1 1 1 1 1 2
7,6 2,757 2,759 2,760 2,762 2,764 2,766 2,768 2,769 2,771 2,773 0 0 1 1 1 1 1 1 2
7,7 2,775 2,777 2,778 2,780 2,782 2,784 2,786 2,787 2,789 2,791 0 0 1 1 1 1 1 1 2
7,8 2,793 2,795 2,796 2,798 2,800 2,802 2,804 2,805 2,807 2,809 0 0 1 1 1 1 1 1 2
7,9 2,811 2,812 2,814 2,816 2,818 2,820 2,821 2,823 2,825 2,827 0 0 1 1 1 1 1 1 2
                    
8,0 2,828 2,830 2,832 2,834 2,835 2,837 2,839 2,841 2,843 2,844 0 0 1 1 1 1 1 1 2
8,1 2,846 2,848 2,850 2,851 2,853 2,855 2,857 2,858 2,860 2,862 0 0 1 1 1 1 1 1 2
8,2 2,864 2,865 2,867 2,869 2,871 2,872 2,874 2,876 2,877 2,879 0 0 1 1 1 1 1 1 2
8,3 2,881 2,883 2,884 2,886 2,888 2,890 2,891 2,893 2,895 2,897 0 0 1 1 1 1 1 1 2
8,4 2,898 2,900 2,902 2,903 2,905 2,907 2,909 2,910 2,912 2,914 0 0 1 1 1 1 1 1 2
                    
8,5 2,915 2,917 2,919 2,921 2,922 2,924 2,926 2,927 2,929 2,931 0 0 1 1 1 1 1 1 2
8,6 2,933 2,934 2,936 2,938 2,939 2,941 2,943 2,944 2,946 2,948 0 0 1 1 1 1 1 1 2
8,7 2,950 2,951 2,953 2,955 2,956 2,958 2,960 2,961 2,963 2,965 0 0 1 1 1 1 1 1 2
8,8 2,966 2,968 2,970 2,972 2,973 2,975 2,977 2,978 2,980 2,982 0 0 1 1 1 1 1 1 2
8,9 2,983 2,985 2,987 2,988 2,990 2,992 2,993 2,995 2,997 2,998 0 0 1 1 1 1 1 1 2
N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9

Поделитесь ссылкой с друзьями:

Похожие таблицы

Комментарии:

Источник

Квадратные корни (Таблица Брадиса 4)

Таблица Брадиса 4 служит для извлечения квадратного корня из любого четырёхзначного числа. Она содержит квадратные корни из всех трёхзначных чисел, заключённых между 1 и 100, вычисленные с 4 значащими цифрами, причём расположение таблицы одинаково с расположением предшествующей таблицы №3. На 4-ю цифру подкоренного числа, если она есть, берётся поправка.

При перенесении запятой в числе N на 2, 4, 6,… мест запятая в числе “корень из N” переносится в ту же сторону на 1, 2, 3,.., места.

Читайте также — как пользоваться таблицами Брадиса
Смотрите — все таблицы Брадиса

N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
1,0 1,000 1,005 1,010 1,015 1,020 1,025 1,030 1,034 1,039 1,044 0 1 1 2 2 3 3 4 4
1,1 1,049 1,054 1,058 1,063 1,068 1,072 1,077 1,082 1,086 1,091 0 1 1 2 2 3 3 4 4
1,2 1,095 1,100 1,105 1,109 1,114 1,118 1,122 1,127 1,131 1,136 0 1 1 2 2 3 3 4 4
1,3 1,140 1,145 1,149 1,153 1,158 1,162 1,166 1,170 1,175 1,179 0 1 1 2 2 3 3 3 4
1,4 1,183 1,187 1,192 1,196 1,200 1,204 1,208 1,212 1,217 1,221 0 1 1 2 2 2 3 3 4
1,5 1,225 1,229 1,233 1,237 1,241 1,245 1,245 1,253 1,257 1,261 0 1 1 2 2 2 3 3 4
1,6 1,265 1,269 1,273 1,277 1,281 1,285 1,288 1,292 1,296 1,300 0 1 1 2 2 2 3 3 3
1,7 1,304 1,303 1,311 1,315 1,319 1,323 1,327 1,330 1,334 1,338 0 1 1 2 2 2 3 3 3
1,8 1,342 1,345 1,34? 1,353 1,356 1.3g0 1,364 1,367 1,371 1,375 0 1 1 1 2 2 3 3 3
1,9 1,378 1,382 1,386 1,389 1,393 1,396 1,400 1,404 1,407 1,411 0 1 1 1 2 2 3 3 3
2,0 1,414 1,418 1,421 1,425 1,428 1,432 1,435 1,439 1,442 1,446 0 1 1 1 2 2 2 3 3
2,1 1,449 1,453 1,456 1,459 1,463 1,466 1,470 1,473 1,476 1,480 0 1 1 1 2 2 2 3 3
2,2 1,483 1,487 1,490 1,493 1,497 1,500 1,503 1,507 1,510 1,513 0 1 1 1 2 2 2 3 3
2,3 1,517 1,520 1,523 1,526 1,530 1,533 1,536 1,539 1,543 1,546 0 1 1 1 2 2 2 3 3
2,4 1,549 1,552 1,556 1,559 1,562 1,565 1,568 1,572 1,575 1,578 0 1 1 1 2 2 2 3 3
2,5 1,581 1,584 1,587 1,591 1,594 1,597 1,600 1,603 1,606 1,609 0 1 1 1 2 2 2 3 3
2,6 1,612 1,616 1,619 1,622 1,625 1,628 1,631 1,634 1,637 1,640 0 1 1 1 2 2 2 2 3
2,7 1,643 1,646 1,649 1,652 1,655 1,658 1,661 1,664 1,667 1,670 0 1 1 1 2 2 2 2 3
2,8 1,673 1,676 1,679 1,682 1,685 1,688 1,691 1,694 1,697 1,700 0 1 1 1 1 2 2 2 3
2,9 1,703 1,706 1,709 1,712 1,715 1,718 1,720 1,723 1,726 1,729 0 1 1 1 1 2 2 2 3
3,0 1,732 1,735 1,738 1,741 1,744 1,746 1,749 1,752 1,755 1,758 0 1 1 1 1 2 2 2 3
3,1 1,761 1,764 1,766 1,769 1,772 1,775 1,778 1,780 1,783 1,786 0 1 1 1 1 2 2 2 3
3,2 1,789 1,792 1,794 1,797 1,800 1,803 1,806 1,808 1,811 1,814 0 1 1 1 1 2 2 2 2
3,3 1,817 1,819 1,822 1,825 1,828 1,830 1,833 1,836 1,838 1,841 0 1 1 1 1 2 2 2 2
3,4 1,844 1,847 1,849 1,852 1,855 1,857 1,860 1,863 1,865 1,868 0 1 1 1 1 2 2 2 2
3,5 1,871 1,873 1,876 1,879 1,881 1,884 1,887 1,889 1,892 1,895 0 1 1 1 1 2 2 2 2
3,6 1,897 1,900 1,903 1,905 1,908 1,910 1,913 1,916 1,918 1,921 0 1 1 1 1 2 2 2 2
3,7 1,924 1,926 1,929 1,931 1,934 1,936 1,939 1,942 1,944 1,947 0 1 1 1 1 2 2 2 2
3,8 1,949 1,952 1,954 1,957 1,960 1,962 1,965 1,967 1,970 1,972 0 1 1 1 1 2 2 2 2
3,9 1,975 1,977 1,980 1,982 1,985 1,987 1,990 1,992 1,995 1,997 0 1 1 1 1 2 2 2 2
4,0 2,000 2,002 2,005 2,007 2,010 2,012 2,015 2,017 2,020 2,022 0 0 1 1 1 1 2 2 2
4,1 2,025 2,027 2,030 2,032 2,035 2,037 2,040 2,042 2,045 2,047 0 0 1 1 1 1 2 2 2
4,2 2,049 2,052 2,054 2.057 2,059 2,062 2,064 2,066 2,069 2,071 0 0 1 1 1 1 2 2 2
4,3 2,074 2,076 2,078 2,081 2,083 2,086 2,088 2,090 2,093 2,095 0 0 1 1 1 1 2 2 2
4,4 2,098 2,100 2,102 2,105 2,107 2,110 2,112 2,114 2,117 2,119 0 0 1 1 1 1 2 2 2
4,5 2,121 2,124 2,126 2,128 2,131 2,133 2,135 2,138 2,140 2,142 0 0 1 1 1 1 2 2 2
4,6 2,145 2,147 2,149 2,152 2.154 2,156 2,159 2.161 2,163 2,166 0 0 1 1 1 1 2 2 2
4,7 2,168 2,170 2,173 2,175 2,177 2,179 2,182 2,184 2,186 2,189 0 0 1 1 1 1 2 2 2
4,8 2,191 2,193 2,195 2,198 2,200 2,202 2,205 2,207 2,209 2,211 0 0 1 1 1 1 2 2 2
4,9 2,214 2,216 2,218 2,220 2,223 2,225 2,227 2,229 2,232 2,234 0 0 1 1 1 1 2 2 2
N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9

При перенесении запятой в числе N на 2, 4, 6,… мест запятая в числе “корень из N” переносится в ту же сторону на 1, 2, 3,.., места.

N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
5,0 2,236 2,238 2,241 2,243 2,245 2,247 2,249 2,252 2,254 2,256 0 0 1 1 1 1 2 2 2
5,1 2,258 2,261 2,263 2,265 2,267 2,269 2,272 2,274 2,276 2,278 0 0 1 1 1 1 2 2 2
5,2 2,280 2,283 2,285 2,287 2,289 2,291 2,293 2,296 2,298 2,300 0 0 1 1 1 1 2 2 2
5,3 2,302 2,304 2,307 2,309 2,311 2,313 2,315 2,317 2,319 2,322 0 0 1 1 1 1 2 2 2
5,4 2,324 2,326 2,328 2,330 2,332 2,335 2,337 2,339 2,341 2,343 0 0 1 1 1 1 1 2 2
5,5 2,345 2,347 2,349 2,352 2,354 2,356 2,358 2,360 2,362 2,364 0 0 1 1 1 1 1 2 2
5,6 2,366 2,369 2,371 2,373 2,375 2,377 2,379 2,381 2,383 2,385 0 0 1 1 1 1 1 2 2
5,7 2,387 2,390 2,392 2,394 2,396 2,398 2,400 2,402 2,404 2,406 0 0 1 1 1 1 1 2 2
5,8 2,408 2,410 2,412 2,415 2,417 2,419 2,421 2,423 2,425 2,427 0 0 1 1 1 1 1 2 2
5,9 2,429 2,431 2,433 2,435 2,437 2,439 2,441 2,443 2,445 2,447 0 0 1 1 1 1 1 2 2
6,0 2,449 2,452 2,454 2,456 2,458 2,460 2,462 2,464 2,466 2,468 0 0 1 1 1 1 1 2 2
6,1 2,470 2,472 2,474 2-,476 2,478 2,480 2,482 2,484 2,486 2,488 0 0 1 1 1 1 1 2 2
6,2 2,490 2,492 2,494 2,496 2,498 2,500 2,502 2,504 2,506 2,508 0 0 1 1 1 1 1 2 2
6,3 2,510 2,512 2,514 2,516 2,518 2,520 2,522 2,524 2,526 2,528 0 0 1 1 1 1 1 2 2
6,4 2,530 2,532 2,534 2,536 2,538 2,540 2,542 2,544 2,546 2,548 0 0 1 1 1 1 1 2 2
6,5 2,550 2,551 2,553 2,555 2,557 2,559 2,561 2,563 2,565 2,567 0 0 1 1 1 1 1 2 2
6,6 2,569 2,571 2,573 2,575 2,577 2,579 2,581 2,583 2,585 2,587 0 0 1 1 1 1 1 2 2
6,7 2,588 2,590 2,592 2,594 2,596 2,598 2,600 2,602 2,604 2,606 0 0 1 1 1 1 1 2 2
6,8 2,608 2,610 2,612 2,613 2,615 2,617 2,619 2,621 2,623 2,625 0 0 1 1 1 1 1 2 2
6,9 2,627 2,629 2,631 2,632 2,634 2,636 2,638 2,640 2,642 2,644 0 0 1 1 1 1 1 2 2
7,0 2,646 2,648 2,650 2,651 2,653 2,655 2,657 2,659 2,661 2,663 0 0 1 1 1 1 1 2 2
7,1 2,665 2,666 2,668 2,670 2,672 2,674 2,676 2,678 2,680 2,681 0 0 1 1 1 1 1 1 2
7,2 2,683 2,685 2,687 2,689 2,691 2,693 2,694 2,696 2,698 2,700 0 0 1 1 1 1 1 1 2
7,3 2,702 2,704 2,706 2,707 2,709 2,711 2,713 2,715 2,717 2,718 0 0 1 1 1 1 1 1 2
7,4 2,720 2,722 2,724 2,726 2,728 2,729 2,731 2,733 2,735 2,737 0 0 1 1 1 1 1 1 2
7,5 2,739 2,740 2,742 2,744 2,746 2,748 2,750 2,751 2,753 2,755 0 0 1 1 1 1 1 1 2
7,6 2,757 2,759 2,760 2,762 2,764 2,766 2,768 2,769 2,771 2,773 0 0 1 1 1 1 1 1 2
7,7 2,775 2,777 2,778 2,780 2,782 2,784 2,786 2,787 2,789 2,791 0 0 1 1 1 1 1 1 2
7,8 2,793 2,795 2,796 2,798 2,800 2,802 2,804 2,805 2,807 2,809 0 0 1 1 1 1 1 1 2
7,9 2,811 2,812 2,814 2,816 2,818 2,820 2,821 2,823 2,825 2,827 0 0 1 1 1 1 1 1 2
8,0 2,828 2,830 2,832 2,834 2,835 2,837 2,839 2,841 2,843 2,844 0 0 1 1 1 1 1 1 2
8,1 2,846 2,848 2,850 2,851 2,853 2,855 2,857 2,858 2,860 2,862 0 0 1 1 1 1 1 1 2
8,2 2,864 2,865 2,867 2,869 2,871 2,872 2,874 2,876 2,877 2,879 0 0 1 1 1 1 1 1 2
8,3 2,881 2,883 2,884 2,886 2,888 2,890 2,891 2,893 2,895 2,897 0 0 1 1 1 1 1 1 2
8,4 2,898 2,900 2,902 2,903 2,905 2,907 2,909 2,910 2,912 2,914 0 0 1 1 1 1 1 1 2
8,5 2,915 2,917 2,919 2,921 2,922 2,924 2,926 2,927 2,929 2,931 0 0 1 1 1 1 1 1 2
8,6 2,933 2,934 2,936 2,938 2,939 2,941 2,943 2,944 2,946 2,948 0 0 1 1 1 1 1 1 2
8,7 2,950 2,951 2,953 2,955 2,956 2,958 2,960 2,961 2,963 2,965 0 0 1 1 1 1 1 1 2
8,8 2,966 2,968 2,970 2,972 2,973 2,975 2,977 2,978 2,980 2,982 0 0 1 1 1 1 1 1 2
8,9 2,983 2,985 2,987 2,988 2,990 2,992 2,993 2,995 2,997 2,998 0 0 1 1 1 1 1 1 2
N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
9.0 3.0 3.002 3.003 3.005 3.007 3.008 3.01 3.012 3.013 3.015 0 0 0 1 1 1 1 1 1
9.1 3.017 3.018 3.02 3.022 3.023 3.025 3.027 3.028 3.03 3.032 0 0 0 1 1 1 1 1 1
9.2 3.033 3.035 3.036 3.038 3.04 3.041 3.043 3.045 3.046 3.048 0 0 0 1 1 1 1 1 1
9.3 3.05 3.051 3.053 3.055 3.056 3.058 3.059 3.061 3.063 3.064 0 0 0 1 1 1 1 1 1
9.4 3.066 3.068 3.069 3.071 3.072 3.074 3.076 3.077 3.079 3.081 0 0 0 1 1 1 1 1 1
9.5 3.082 3.084 3.085 3.087 3.089 3.09 3.092 3.094 3.095 3.097 0 0 0 1 1 1 1 1 1
9.6 3.098 3.1 3.102 3.103 3.105 3.106 3.108 3.11 3.111 3.113 0 0 0 1 1 1 1 1 1
9.7 3.114 3.116 3.118 3.119 3.121 3.122 3.124 3.126 3.127 3.129 0 0 0 1 1 1 1 1 1
9.8 3.13 3.132 3.134 3.135 3.137 3.138 3.140 3.142 3.143 3.145 0 0 0 1 1 1 1 1 1
9.9 3.146 3.148 3.15 3.151 3.153 3.154 3.156 3.158 3.159 3.161 0 0 0 1 1 1 1 1 1
N 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
10 3.162 3.178 3.194 3.209 3.225 3.24 3.256 3.271 3.286 3.302 1 3 5 6 8 9 11 12 14
11 3.317 3.332 3.347 3.362 3.376 3.391 3.406 3.421 3.435 3.450 1 3 4 6 7 9 10 12 13
12 3.464 3.479 3.493 3.507 3.521 3.536 3.55 3.564 3.578 3.592 1 3 4 6 7 8 10 11 13
13 3.606 3.619 3.633 3.647 3.661 3.674 3.688 3.701 3.715 3.728 1 3 4 5 7 8 10 11 12
14 3.742 3.755 3.768 3.782 3.795 3.808 3.821 3.834 3.847 3.86 1 3 4 5 7 8 9 11 12
15 3.873 3.886 3.899 3.912 3.924 3.937 3.95 3.962 3.975 3.987 1 3 4 5 6 8 9 10 11
16 4.0 4.012 4.025 4.037 4.05 4.062 4.074 4.087 4.099 4.111 1 2 4 5 6 7 9 10 11
17 4.123 4.135 4.147 4.159 4.171 4.183 4.195 4.207 4.219 4.231 1 2 4 5 6 7 8 10 11
18 4.243 4.254 4.266 4.278 4.29 4.301 4.313 4.324 4.336 4.347 1 2 3 5 6 7 8 9 10
19 4.359 4.37 4.382 4.393 4.405 4.416 4.427 4.438 4.45 4.461 1 2 3 5 6 7 8 9 10
20 4.472 4.483 4.494 4.506 4.517 4.528 4.539 4.55 4.561 4.572 1 2 3 4 6 7 8 9 10
21 4.583 4.593 4.604 4.615 4.626 4.637 4.648 4.658 4.669 4.68 1 2 3 4 5 6 8 9 10
22 4.69 4.701 4.712 4.722 4.733 4.743 4.754 4.764 4.775 4.785 1 2 3 4 5 6 7 8 9
23 4.796 4.806 4.817 4.827 4.837 4.848 4.858 4.868 4.879 4.889 1 2 3 4 5 6 7 8 9
24 4.899 4.909 4.919 4.93 4.94 4.95 4.96 4.97 4.98 4.99 1 2 3 4 5 6 7 8 9
25 5.0 5.01 5.02 5.03 5.04 5.05 5.06 5.07 5.079 5.089 1 2 3 4 5 6 7 8 9
26 5.099 5.109 5.119 5.128 5.138 5.148 5.158 5.167 5.177 5.187 1 2 3 4 5 6 7 8 9
27 5.196 5.206 5.215 5.225 5.235 5.244 5.254 5.263 5.273 5.282 1 2 3 4 5 6 7 8 9
28 5.292 5.301 5.31 5.32 5.329 5.339 5.348 5.357 5.367 5.376 1 2 3 4 5 6 7 7 8
29 5.385 5.394 5.404 5.413 5.422 5.431 5.441 5.45 5.459 5.468 1 2 3 4 5 5 6 7 8
30 5.477 5.486 5.495 5.505 5.514 5.523 5.532 5.541 5.55 5.559 1 2 3 4 4 5 6 7 8
31 5.568 5.577 5.586 5.595 5.604 5.612 5.621 5.63 5.639 5.648 1 2 3 3 4 5 6 7 8
32 5.657 5.666 5.675 5.683 5.692 5.701 5.71 5.718 5.727 5.736 1 2 3 3 4 5 6 7 8
33 5.745 5.753 5.762 5.771 5.779 5.788 5.797 5.805 5.814 5.822 1 2 3 3 4 5 6 7 8
34 5.831 5.84 5.848 5.857 5.865 5.874 5.882 5.891 5.899 5.908 1 2 3 3 4 5 6 7 8
35 5.916 5.925 5.933 5.941 5.95 5.958 5.967 5.975 5.983 5.992 1 2 3 3 4 5 6 7 8
36 6.0 6.008 6.017 6.025 6.033 6.042 6.05 6.058 6.066 6.075 1 2 2 3 4 5 6 7 7
37 6.083 6.091 6.099 6.107 6.116 6.124 6.132 6.14 6.148 6.156 1 2 2 3 4 5 6 7 7
38 6.164 6.173 6.181 6.189 6.197 6.205 6.213 6.221 6.229 6.237 1 2 2 3 4 5 6 6 7
39 6.245 6.253 6.261 6.269 6.277 6.285 6.293 6.301 6.309 6.317 1 2 2 3 4 5 6 6 7
40 6.325 6.332 6.34 6.348 6.356 6.364 6.372 6.38 6.387 6.395 1 2 2 3 4 5 6 6 7
41 6.403 6.411 6.419 6.427 6.434 6.442 6.45 6.458 6.465 6.473 1 2 2 3 4 5 5 6 7
42 6.481 6.488 6.496 6.504 6.512 6.519 6.527 6.535 6.542 6.55 1 2 2 3 4 5 5 6 7
43 6.557 6.565 6.573 6.58 6.588 6.595 6.603 6.611 6.618 6.626 1 2 2 3 4 5 5 6 7
44 6.633 6.641 6.648 6.656 6.663 6.671 6.678 6.686 6.693 6.701 1 2 2 3 4 5 5 6 7
45 6.708 6.716 6.723 6.731 6.738 6.745 6.753 6.76 6.768 6.775 1 1 2 3 4 4 5 6 7
46 6.782 6.79 6.797 6.804 6.812 6.819 6.826 6.834 6.841 6.848 1 1 2 3 4 4 5 6 7
47 6.856 6.863 6.87 6.877 6.885 6.892 6.899 6.907 6.914 6.921 1 1 2 3 4 4 5 6 7
48 6.928 6.935 6.943 6.95 6.957 6.964 6.971 6.979 6.986 6.993 1 1 2 3 4 4 5 6 6
49 7.0 7.007 7.014 7.021 7.029 7.036 7.043 7.05 7.057 7.064 1 1 2 3 4 4 5 6 6
50 7.071 7.078 7.085 7.092 7.099 7.106 7.113 7.12 7.127 7.134 1 1 2 3 4 4 5 6 6
51 7.141 7.148 7.155 7.162 7.169 7.176 7.183 7.19 7.197 7.204 1 1 2 3 3 4 5 6 6
52 7.211 7.218 7.225 7.232 7.239 7.246 7.253 7.259 7.266 7.273 1 1 2 3 3 4 5 6 6
53 7.28 7.287 7.294 7.301 7.308 7.314 7.321 7.328 7.335 7.342 1 1 2 3 3 4 5 5 6
54 7.348 7.355 7.362 7.369 7.376 7.382 7.389 7.396 7.403 7.409 1 1 2 3 3 4 5 5 6
55 7.416 7.423 7.43 7.436 7.443 7.45 7.457 7.463 7.47 7.477 1 1 2 3 3 4 5 5 6
56 7.483 7.49 7.497 7.503 7.51 7.517 7.523 7.53 7.537 7.543 1 1 2 3 3 4 5 5 6
57 7.55 7.556 7.563 7.57 7.576 7.583 7.589 7.596 7.603 7.609 1 1 2 3 3 4 5 5 6
58 7.616 7.622 7.629 7.635 7.642 7.649 7.655 7.662 7.668 7.675 1 1 2 3 3 4 5 5 6
59 7.681 7.688 7.694 7.701 7.707 7.714 7.72 7.727 7.733 7.74 1 1 2 3 3 4 4 5 6
60 7.746 7.752 7.759 7.765 7.772 7.778 7.785 7.791 7.797 7.804 1 1 2 3 3 4 4 5 6
61 7.81 7.817 7.823 7.829 7.836 7.842 7.849 7.855 7.861 7.868 1 1 2 3 3 4 4 5 6
62 7.874 7.88 7.887 7.893 7.899 7.906 7.912 7.918 7.925 7.931 1 1 2 3 3 4 4 5 6
63 7.937 7.944 7.95 7.956 7.962 7.969 7.975 7.981 7.987 7.994 1 1 2 3 3 4 4 5 6
64 8.0 8.006 8.012 8.019 8.025 8.031 8.037 8.044 8.05 8.056 1 1 2 2 3 4 4 5 6
65 8.062 8.068 8.075 8.081 8.087 8.093 8.099 8.106 8.112 8.118 1 1 2 2 3 4 4 5 6
66 8.124 8.13 8.136 8.142 8.149 8.155 8.161 8.167 8.173 8.179 1 1 2 2 3 4 4 5 5
67 8.185 8.191 8.198 8.204 8.21 8.216 8.222 8.228 8.234 8.24 1 1 2 2 3 4 4 5 5
68 8.246 8.252 8.258 8.264 8.27 8.276 8.283 8.289 8.295 8.301 1 1 2 2 3 4 4 5 5
69 8.307 8.313 8.319 8.325 8.331 8.337 8.343 8.349 8.355 8.361 1 1 2 2 3 4 4 5 5
70 8.367 8.373 8.379 8.385 8.39 8.396 8.402 8.408 8.414 8.42 1 1 2 2 3 4 4 5 5
71 8.426 8.432 8.438 8.444 8.45 8.456 8.462 8.468 8.473 8.479 1 1 2 2 3 4 4 5 5
72 8.485 8.491 8.497 8.503 8.509 8.515 8.521 8.526 8.532 8.538 1 1 2 2 3 3 4 5 5
73 8.544 8.55 8.556 8.562 8.567 8.573 8.579 8.585 8.591 8.597 1 1 2 2 3 3 4 5 5
74 8.602 8.608 8.614 8.62 8.626 8.631 8.637 8.643 8.649 8.654 1 1 2 2 3 3 4 5 5
75 8.66 8.666 8.672 8.678 8.683 8.689 8.695 8.701 8.706 8.712 1 1 2 2 3 4 4 5 5
76 8.718 8.724 8.729 8.735 8.741 8.746 8.752 8.758 8.764 8.769 1 1 2 2 3 3 4 5 5
77 8.775 8.781 8.786 8.792 8.798 8.803 8.809 8.815 8.82 8.826 1 1 2 2 3 3 4 4 5
78 8.832 8.837 8.843 8.849 8.854 8.86 8.866 8.871 8.877 8.883 1 1 2 2 3 3 4 4 5
79 8.888 8.894 8.899 8.905 8.911 8.916 8.922 8.927 8.933 8.939 1 1 2 2 3 3 4 4 5
80 8.944 34912 8.955 8.961 8.967 8.972 8.978 8.983 8.989 8.994 1 1 2 2 3 3 4 4 5
81 9.0 9.006 9.011 9.017 9.022 9.028 9.033 9.039 9.044 9.05 1 1 2 2 3 3 4 4 5
82 9.055 9.061 9.066 9.072 9.077 9.083 9.088 9.094 9.099 9.105 1 1 2 2 3 3 4 4 5
83 9.10 9.116 9.121 9.127 9.132 9.138 9.143 9.149 9.154 9.16 1 1 2 2 3 3 4 4 5
84 9.165 9.171 9.176 9.182 9.187 9.192 9.198 9.203 9.209 9.214 1 1 2 2 3 3 4 4 5
85 9.22 9.225 9.23 9.236 9.241 9.247 9.252 9.257 9.263 9.268 1 1 2 2 3 3 4 4 5
86 9.274 9.279 9.284 9.29 9.295 9.301 9.306 9.311 9.317 9.322 1 1 2 2 3 3 4 4 5
87 9.327 9.333 9.338 9.343 9.349 9.354 9.359 9.365 9.37 9.375 1 1 2 2 3 3 4 4 5
88 9.381 9.386 9.391 9.397 9.402 9.407 9.413 9.418 9.423 9.429 1 1 2 2 3 3 4 4 5
89 9.434 9.439 9.445 9.45 9.455 9.46 9.466 9.471 9.476 9.482 1 1 2 2 3 3 4 4 5
90 9.487 9.492 9.497 9.503 9.508 9.513 9.518 9.524 9.529 9.534 1 1 2 2 3 3 4 4 5
91 9.539 9.545 9.55 9.555 9.56 9.566 9.571 9.576 9.581 9.586 1 1 2 2 3 3 4 4 5
92 9.592 9.597 9.602 9.607 9.612 9.618 9.623 9.628 9.633 9.638 1 1 2 2 3 3 4 4 5
93 9.644 9.649 9.654 9.659 9.664 9.67 9.675 9.68 9.685 9.69 1 1 2 2 3 3 4 4 5
94 9.695 9.701 9.706 9.711 9.716 9.721 9.726 9.731 9.737 9.742 1 1 2 2 3 3 4 4 5
95 9.747 9.752 9.757 9.762 9.767 9.772 9.778 9.783 9.788 9.793 1 1 2 2 3 3 4 4 5
96 9.798 9.803 9.808 9.813 9.818 9.823 9.829 9.834 9.839 9.844 1 1 2 2 3 3 4 4 5
97 9.849 9.854 9.859 9.864 9.869 9.874 9.879 9.884 9.889 9.894 1 1 2 2 3 3 4 4 5
98 9.899 9.905 9.91 9.915 9.92 9.925 9.93 9.935 9.94 9.945 0 1 1 2 2 3 3 4 4
99 9.95 9.955 9.96 9.965 9.97 9.975 9.98 9.985 9.99 9.995 0 1 1 2 2 3 3 4 4

Как пользоваться таблицей Брадиса квадратных корней.

Как пользоваться таблицей Брадиса? Таблица Брадиса квадратных корней используется для извлечения квадратного корня из любого 4-х-значного числа. В ней содержатся квадратные корни из всех 3-х-значных чисел, которые расположены между единицей и сотней, вычисленные с четырьмя значащими цифрами, при этом расположение таблицы одинаково с расположением остальных таблиц. На четвертую цифру подкоренного числа, если она есть, берут поправку.

Например:

 (строка 9.7, столбец 3);

 (строка 36, столбец 4);

 (к корню 3.119 прибавлена поправка на 6, равная 1);

 (к корню 6.033 прибавили поправку на 8, которая равна 7, либо от корня 6.042 отнимаем поправку на 2, равную 2).

Источник

Макеты страниц

Извлечение квадратного корня по таблицам. В § 93 на примере извлечения квадратного корня из числа 20 мы показали, как можно вычислить приближённо с необходимой степенью точности. Однако, даже для того чтобы найти искомый корень с точностью до 0,01, пришлось проделать много вычислений. Чтобы облегчить вычислительную работу, составлены специальные таблицы квадратных корней, в которых даны приближённые значения квадратных корней из чисел.

В таблицах В. М. Брадиса даны квадратные корни с точностью до 0,001 чисел от 1 до 10 с промежутком в 0,01 и чисел от 10 до 100 с промежутком в 0,1. Устройство и употребление таблицы такое же, как и таблицы квадратов.

Поясним на примерах, как следует пользоваться таблицами квадратных корней.

. В первом столбце находим число 6,7 и рядом с ним во втором столбце квадратный корень из него: 2,588 (по округлении получим 2,6).

. В первом столбце находим число 27; в этом же ряду в столбце под номером 6 находим: (по округлении получим: 5,25).

. По предыдущему находим: . В столбце «поправок» за № 4 находим число

3, которое прибавляем к последней цифре числа 7,503. Получаем: .

. Подкоренное число можно записать так:

тогда

(или по округлении 20,7).

Чтобы получить подкоренное число 427, мы должны в числе 4,27, которое содержится в таблице, передвинуть запятую на два знака вправо, тогда в результате 2,066, взятом из таблицы, придётся перенести запятую в ту же сторону на один знак.

. Находим Тогда Это нетрудно объяснить. Число 28,68, корень из которого находится по таблице, в 100 раз больше подкоренного числа.

Значит, правильный результат будет в 10 раз меньше результата, найденного из таблицы.

Поясним подробнее эту запись. Сначала находим затем к последнему знаку прибавляем поправку, равную 1, тогда

Увеличив результат в 100 раз, получим:

7) Вычислить значение выражения при

Решение. Находим по таблицам:

(третьи цифры оставлены как запасные).

Умножаем:

Складываем:

Примечание. Если два числа состоят из одних и тех же значащих цифр, то отсюда ещё не следует, что квадратные корни из этих чисел также состоят из одних и тех же значащих цифр.

Поясним это такими примерами:

Извлечение квадратного корня на счётной линейке. Так как извлечение квадратного корня есть действие, обратное возведению чисел в квадрат, то для вычисления квадратного корня пользуемся теми же шкалами, что и при возведении в квадрат, то есть шкалой квадратов А и основной шкалой

Но действие извлечения квадратного корня производится в порядке, обратном действию возведения в квадрат. При возведении в квадрат мы основание отмечали визиром на шкале и результат читали на шкале А. Здесь же, наоборот, значение подкоренного числа отмечаем визирной чертой на шкале квадратов А и против визирной черты на основной шкале читаем значение корня. На чертеже 39 находим;

Если надо найти то визирную черту ставим против 40 в правой половине шкалы квадратов и читаем ответ на основной шкале; 6,32.

Извлечение квадратного корня из любых чисел можно свести к одному из двух рассмотренных случаев.

В качестве примеров возьмём те числа, из которых мы на страницах 216—217 извлекали квадратный корень по таблицам:

Теперь сформулируем правило извлечения квадратного корня:

1) Подкоренное число представляем в виде однозначного или двузначного числа, умножив (или разделив) его на чётную степень десяти.

2) Если подкоренное число представлено в виде однозначного числа, его устанавливают визиром на левой половине квадратной шкалы А; если же оно представлено двузначным числом, то — на правой половине квадратной шкалы.

3) Результат отсчитывается по визиру на основной шкале.

Существует другое правило, позволяющее определить, в какой половине шкалы квадратов следует установить подкоренное число при извлечении квадратного корня.

Подкоренное число разбивают на грани, по две цифры в каждой грани, влево от запятой, если число больше 1, и вправо от запятой, если число меньше 1.

Если первая слева грань (не считая граней, состоящих из одних нулей) содержит одну значащую цифру, то число устанавливается в левой половине шкалы квадратов, если же в этой грана две цифры, то — в правой половине.

Например: .

Пользуясь этим способом, легко установить значность числа и положение запятой, так как каждая грань подкоренного числа, стоящая слева от запятой, даёт у корня один знак до запятой, а каждая чисто нулевая грань справа от запятой (если подкоренное число меньше единицы) даёт у корня один нуль после запятой.

1

Оглавление

  • ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.
  • § 2. Алгебраические выражения.
  • § 3. Допустимые значения букв.
  • § 4. Порядок действий.
  • § 5. Основные законы сложения и умножения.
  • § 6. Краткие исторические сведения.
  • ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.
  • § 7. Положительные и отрицательные числа.
  • § 8. Числовая ось.
  • § 9. Противоположные числа.
  • § 10. Абсолютная величина числа.
  • § 11. Сравнение рациональных чисел.
  • § 12. Сложение рациональных чисел.
  • § 13. Сложение нескольких чисел.
  • § 14. Законы сложения.
  • § 15. Вычитание рациональных чисел.
  • § 16. Алгебраическая сумма.
  • § 17. Умножение.
  • § 18. Умножение нескольких чисел.
  • § 19. Законы умножения.
  • § 20. Деление.
  • § 21. Свойства деления.
  • § 22. Возведение в степень.
  • § 23. Порядок выполнения действий.
  • § 24. Уравнения.
  • § 25. Решение задач с помощью уравнений.
  • § 26. Графики.
  • § 27. Краткие исторические сведения. (Из истории отрицательных чисел.)
  • ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.
  • § 28. Одночлен и многочлен.
  • § 29. Тождества и тождественные преобразования.
  • § 30. Коэффициент.
  • § 31. Расположенные многочлены.
  • § 32. Приведение подобных членов.
  • § 33. Сложение одночленов и многочленов.
  • § 34. Противоположные многочлены.
  • § 35. Вычитание одночленов и многочленов
  • § 36. Умножение одночленов.
  • § 37. Умножение многочлена на одночлен.
  • § 38. Умножение многочленов.
  • § 39. Умножение расположенных многочленов.
  • § 40. Возведение одночленов в степень.
  • § 41. Формулы сокращённого умножения.
  • § 42. Общие замечания о делении целых алгебраических выражений.
  • § 43. Деление одночленов.
  • § 44. Деление многочлена на одночлен
  • § 45. Примеры решения уравнений.
  • ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ.
  • § 47. Равносильные уравнения.
  • § 48. Два основных свойства уравнений.
  • § 49. Уравнения, содержащие неизвестное в обеих частях.
  • § 50. Уравнение первой степени с одним неизвестным.
  • § 51. Общие указания к решению уравнений.
  • § 52. Решение задач с помощью уравнений.
  • § 53. Краткие исторические сведения. (Из истории уравнений.)
  • ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.
  • § 54. Понятие о разложении на множители.
  • § 55. Вынесение за скобки общего множителя.
  • § 56. Способ группировки.
  • § 57. Применение формул сокращённого умножения.
  • § 58. Применение нескольких способов.
  • § 59. Деление многочленов при помощи разложения на множители.
  • ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.
  • § 60. Понятие об алгебраической дроби.
  • § 61. Основное свойство дроби и сокращение дробей.
  • § 62. Перемена знака у членов дроби.
  • § 63. Целая отрицательная и нулевая степени числа.
  • § 64. Приведение дробей к общему знаменателю.
  • § 65. Сложение дробей.
  • § 66. Вычитание дробей.
  • § 67. Умножение дробей.
  • § 68. Деление дробей.
  • § 69. Возведение дроби в натуральную степень.
  • § 70. Дробные уравнения.
  • § 71. Примеры решения уравнений с буквенными коэффициентами.
  • ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
  • § 72. Координаты точки на плоскости.
  • § 73. Прямо пропорциональная зависимость.
  • § 74. График прямо пропорциональной зависимости.
  • § 75. Линейная зависимость.
  • § 76. Обратно пропорциональная зависимость.
  • ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ.
  • § 77. Уравнение первой степени с двумя неизвестными.
  • § 78. Система двух уравнений первой степени с двумя неизвестными.
  • § 79. Равносильные системы.
  • § 80. Решение систем уравнений.
  • § 81. Графическое решение системы двух уравнений.
  • § 82. Решение задач.
  • § 83. Уравнение с тремя неизвестными.
  • § 84. Система трёх уравнений с тремя неизвестными.
  • ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА.
  • § 85. Равномерные и неравномерные шкалы.
  • § 86. Устройство счётной (логарифмической) линейки.
  • § 87. Основная шкала.
  • § 88. Умножение и деление с помощью счётной линейки.
  • ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ.
  • § 89. Построение графика зависимости y = x^2
  • § 90. Вычисление квадратов чисел по таблицам и при помощи счётной линейки.
  • § 91. Понятие об извлечении корня. Решим две задачи.
  • § 92. Арифметический корень.
  • § 93. Приближённый квадратный корень из положительного числа.
  • § 94. График зависимости y = sqrt(х).
  • § 95. Извлечение квадратного корня из целых чисел.
  • § 96. Извлечение корня с точностью до 0,1; 0,01 и т. д.
  • § 97. Квадратный корень из произведения, дроби и степени.
  • § 98. Простейшие преобразования.
  • § 99. Извлечение квадратного корня по таблицам и при помощи счётной линейки.
  • § 100. Краткие исторические сведения.
  • ГЛАВА ОДИННАДЦАТАЯ. КВАДРАТНЫЕ УРАВНЕНИЯ.
  • § 101. Квадратные уравнения.
  • § 102. Уравнение вида ax^2+bx=0
  • § 103. Уравнение вида ax^2+c=0
  • § 104. Приведённое квадратное уравнение.
  • § 105. Квадратное уравнение общего вида.
  • § 106. Дискриминант.
  • § 107. Графическое решение квадратного уравнения.
  • § 108. Решение задач, приводящих к квадратным уравнениям.
  • § 109. Теорема Виета.
  • § 110. Исследование корней квадратного уравнения.
  • § 111. Разложение квадратного трёхчлена на множители.
  • § 112. Системы двух уравнений, из которых одно второй и одно первой степени.
  • § 113. Краткие исторические сведения.
  • ГЛАВА ДВЕНАДЦАТАЯ. ФУНКЦИИ И ГРАФИКИ.
  • § 114. Переменные величины.
  • § 115. Понятие о функциональной зависимости.
  • § 116. Аргумент и функция.
  • § 117. Способы задания функции.
  • § 118. Функция y = kx.
  • § 119. Линейная функция.
  • § 120. Трехчлен второй степени.
  • § 121. График функции y=x^2+n
  • § 122. График функции y = (x+m)^2
  • § 123. График трехчлена y = x^2+px+q
  • § 124. График трехчлена y = ax^2+bx+c
  • § 125. Возрастание и убывание квадратного трёхчлена.
  • § 126. Функция у = х^3 и её график.
  • § 127. Понятие о кубическом корне.
  • § 128. Приближённое извлечение кубического корня.
  • § 129. График функции y = x^(1/3)
  • § 130. Примеры графического решения уравнений и систем уравнений.
Источник

Два способа.

Во-первых, квадратный корень – это число в степени 1/2. Так что можно воспользоваться функцией “x^y” (доступна при выборе режима “Инженерный”): набрать число, нажать эту кнопочку, набрать 0,5 и нажать Enter.

Во-вторых, извлечение корня есть операция, обратная возведению в квадрат. А в калькуляторе (опять же в режиме “Инженерный”) есть специальный флажок инверсной функции Inv. Так что наберите число, отметьте этот флажок (или нажмите кнопочку Inv) и нажмите кнопочку “х квадрат”. Отмазка: в калькуляторе из Windows 7 этот способ почему-то не работает.

модератор выбрал этот ответ лучшим

CyBea­r
[5.2K]

более года назад 

Извлечение корня из числа

Извлечение квадратного корня из числа подразумевает нахождение такого числа, которое будучи возведенным в квадрат (умноженное самое на себя) даст при этом первоначальное число. Так например, квадратным корнем из 36 будет являться число 6, так как 6*6 = 6^6 = 36. Для обозначения операции извлечения корня в математике используют специальный символ – “√”. А в программировании функция извлечения квадратного корня чаще всего называется “sqrt” сокращенное от английского “SQuare RooT”, что дословно и переводится как “квадратный корень”.

Ради примера поищем квадратный корень числа 12. Чтобы найти квадратный корень можно:

1. Воспользоваться калькулятором, ввести 12 и найти символ “√”. Получим число 3,464101615137754587­0548926830117 ~ 3,464

Квадратный корень из числа 12 на калькуляторе

2. Воспользоваться таблицей Брадиса для извлечения квадратных корней в диапазоне 0-99 и найти на пересечении соответствующей строки (десятки) и столбца (единицы) искомое значение 3,4641

Таблица Брадиса квадратный корень 12

3. Еще одним вариантом может быть использование универсального алгоритма, который называют “вавилонский”. Он описывается формулой √c= √(a^2+b)=a+b/2a и дает приблизительное вычисления корня с точностью, которая часто бывает достаточной. Для числа 12 вычисление по этой формуле будет выглядеть так: √12 = √(3^2+3)=3+3/(2*3) = 3+1/2 = 3,5. И это достаточно точное вычисление!

В калькуляторе Windows ничего сложного нет извлечь квадратный корень – эта функция заложена в классической форме калькулятора – достаточно ввести число и нажать на значок корня.

Чтобы извлечь корень кубический или произвольный степени следует воспользоваться уже инженерным калькулятором. Для этого в меню Вид выбираем вкладку Инженерный. Получаем такую картинку:

Кубический корень уже есть по умолчанию на панели калькулятора и просто вводим число и нажимаем нужную кнопку, а корень произвольной степени находится так:

Сперва вводим радикал, то есть подкоренное выражение, например 64, нажимаем кнопку корень у из х (смотри в пятом столбике) и далее нажимаем нужную нам степень корня, например 4. Жмем на равно и получаем ответ – 2.

Вот мы и посчитали, что корень четвертой степени из 64 равен 2.

Galin­a7v7
[120K]

7 лет назад 

Многие корни можно извлечь устно.Для этого необходимо знать хоть немного ряд квадратов чисел:1,4,9,16,25,36,49,64,81,121,144,169,196,225,256,,,и по возможности квадраты двузначных чисел,если часто решаете такие задачи.При извлечении квадратов помогает разложение на множители подкоренного числа,и извлечь сомножители,если там будут квадраты чисел.Если и этого не окажется,то постараться проанализировать-между какими квадратами расположено подкоренное число,чтобы определить уровни.Эти анализы подходят для квадратов целых чисел,и для устного вычисления корня.Вычисление неточных корней подходит извлечение по калькулятору,или по таблице корней.

Корень из числа можно извлечь в MS Excel задав, =число^(1/n), где n – корень n-й степени. Например, корень 4-й степени из 81 будет задаваться =81^(1/4) и ответ будет 3. Или выбрав среди математических функций в Эксель СТЕПЕНЬ(число; степень) и записав =СТЕПЕНЬ(81; 1/4)

Быстр­ый Стриж
[1.7K]

7 лет назад 

Корень из числа можно вычислить умножив исходное число на степень 1/2 или произвести вычисление на любом калькуляторе, используя математический значок корня.

Корень числа редко бывает целым значением и чаще всего округляется.

Знаете ответ?
Источник

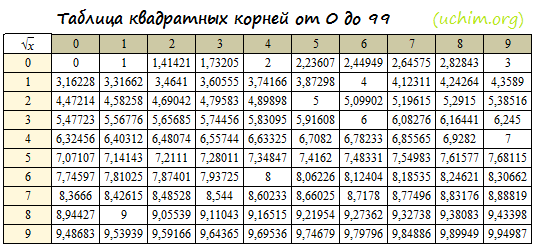
Таблица корней – это таблица, с помощью которой можно извлекать квадратные корни чисел от 0 до 99. Пользоваться таблицей очень легко. Просто выберите число десятков по вертикали и число единиц по горизонтали, результат будет на их пересечении. Например, √36=6. 3 выбирается слева, 6 – сверху. Возможно, вам также будет интересна таблица квадратов.

Извлечение корней онлайн

√

https://uchim.org/matematika/tablica-kornej – uchim.org

Таблица корней по алгебре (числа от 0 до 99, округление до пятого знака)

√x 0 1 2 3 4 5 6 7 8 9
0 0 1 1,41421 1,73205 2 2,23607 2,44949 2,64575 2,82843 3
1 3,16228 3,31662 3,4641 3,60555 3,74166 3,87298 4 4,12311 4,24264 4,3589
2 4,47214 4,58258 4,69042 4,79583 4,89898 5 5,09902 5,19615 5,2915 5,38516
3 5,47723 5,56776 5,65685 5,74456 5,83095 5,91608 6 6,08276 6,16441 6,245
4 6,32456 6,40312 6,48074 6,55744 6,63325 6,7082 6,78233 6,85565 6,9282 7
5 7,07107 7,14143 7,2111 7,28011 7,34847 7,4162 7,48331 7,54983 7,61577 7,68115
6 7,74597 7,81025 7,87401 7,93725 8 8,06226 8,12404 8,18535 8,24621 8,30662
7 8,3666 8,42615 8,48528 8,544 8,60233 8,66025 8,7178 8,77496 8,83176 8,88819
8 8,94427 9 9,05539 9,11043 9,16515 9,21954 9,27362 9,32738 9,38083 9,43398
9 9,48683 9,53939 9,59166 9,64365 9,69536 9,74679 9,79796 9,84886 9,89949 9,94987

Таблица корней в виде компактной картинки (удобно для шпаргалки, например, в 8 классе):

таблица корней

Всё для учебы » Математика в школе » Таблица корней по алгебре

Источник

Добавить комментарий