Таблица истинности информатика 8 класс как составить таблицу истинности

Сегодня мы узнаем, какие
существуют правила для построения таблицы истинности для логических выражений,
в которых количество логических операций больше одной. Также познакомимся со
свойствами логических операций.

Прежде всего давайте
вспомним логические операции, которые мы с вами изучали на прошлом уроке. К ним
относятся инверсия, конъюнкция и дизъюнкция. Рассмотрите
внимательно таблицу с обозначениями логических операций, которые мы будем
использовать в дальнейшем.

Конъюнкция
– это логическая операция, которая объединяет два высказывания в одно новое,
которое будет являться истинным тогда и только тогда, когда оба исходных
высказывания истинны.

Дизъюнкция
– это логическая операция, которая объединяет два высказывания в одно новое,
которое будет являться ложным тогда и только тогда, когда ложны оба исходных
высказывания.

Инверсия
– это логическая операция, которая преобразует исходное высказывание в новое,
значение которого противоположно исходному.

Логические выражения
могут состоять из более чем двух логических операций. В тоже время, для любых
логических выражений можно построить таблицу истинности, в которой мы сможем
увидеть, какие значения принимает выражение. Логические операции выполняются
в следующем порядке: инверсия, конъюнкция и дизъюнкция.

Итак, для начала
рассмотрим, какие действия следует выполнить для построения
таблицы истинности:

1. Подсчитать n
– число переменных в выражении.

(А
V B)
& C.

Мы с вами знаем, что
переменные обозначаются с помощью букв латинского алфавита.

n
= 3.

2. Подсчитать общее число
логических операций в выражении.

Количество
логических операций: 2

То есть нам нужно
сосчитать сколько в нашем выражении инверсий, конъюнкций и дизъюнкций.

3. Установить последовательность
выполнения логических операций с учётом скобок и приоритетов. Как мы с вами
знаем, сначала выполняются операции в скобках, затем инверсия, конъюнкция и
дизъюнкция.

4. Определить число
столбцов в таблице: число переменных плюс число операций. То есть нам нужно
сложить количество переменных и логических операций. Мы получим число столбцов
в таблице.

3
+ 2 =5.

Количество
столбцов: 5.

5. Заполнить шапку
таблицы, включив в неё переменные и операции в соответствии с последовательностью,
установленной в пункте три. То есть мы сначала пишем в шапке таблицы все наши
переменные. Затем операции в порядке их следования.

6. Определить число строк
в таблице (не считая шапки таблицы):

m
= 2ⁿ.

m
– это количество строк. n
– число переменных в выражении. То есть, если наше логическое выражение будет
состоять, например, из трёх переменных, то количество строк m
=
2³ = 8. Шапка не входит в количество этих строк.

7. Выписать наборы
входных переменных с учётом того, что они представляют собой ряд целых n-разрядных
двоичных чисел от 0 до 2ⁿ
–
1. Здесь мы должны написать все возможные входные переменные, как мы делали при
построении таблиц истинности.

8. Провести заполнение
таблицы по столбцам, выполняя логические операции в соответствии с
установленной последовательностью. То есть произвести логические операции с
входными данными в зависимости от логической операции.

А теперь давайте
разберёмся на примере. Необходимо построить таблицу истинности для следующего
логического выражения: (A
& B) & A
V B.

Исходя из первого пункта
плана построения таблицы истинности, нам нужно посчитать число переменных в
выражении. Их у нас две: n
= 2. А и B.

Общее число логических
операций 3.

А сейчас давайте
установим последовательность выполнения логических операций. Сначала будут
выполняться логическая операция в скобках – конъюнкция. То есть первым будет
выполнятся действие А & B.

Вторая логическая
операция снова конъюнкция. И третья логическая операция – дизъюнкция.

Так как у нас 2
переменных и 3 логических операции, значит столбцов у нас будет 5. Так как в
четвёртом пункте указан именно такой способ подсчёта столбцов.

Заполним теперь шапку
таблицы. Сначала будут идти переменные А и B.
Затем логические операции в порядке их выполнения.

Определимся с количеством
строк. Нам дана формула для вычисления строк:

m
=
2ⁿ.

n
= 2.

m
=
2² = 4.

Теперь необходимо
выписать наборы входных данных. То есть заполнить два первых столбца.

2²
– 1= 4 – 1 = 3

Нам необходимо заполнить
столбцы числами от 0 до 3. Так как все операции мы производим в двоичной
системе счисления, то представим числа от 0 до 3 в двухразрядном двоичном коде.
Получим следующие числа:

0₁₀
= 00₂

1₁₀
= 01₂

2₁₀
= 10₂

3₁₀
= 11₂

Теперь занесём эти числа
в первый и второй столбцы. По одной цифре в ячейку.

А сейчас заполним все
остальные столбцы. Первая операция – конъюнкция. Данные будем вносить в третий
столбец. Прежде, чем начать заполнение таблицы истинности вспомним правило
для конъюнкции: новое высказывание будет истинно тогда и только тогда,
когда исходные высказывания истинны. Значит в четвёртой строке для данного
столбца будет стоять 1, так как это единственный случай, когда истинны оба исходных
высказывания, значит и новое будет истинно. В первых трёх строках этого же
столбца будут стоять нули, так как в первой строке ложны оба высказывания, во
второй – высказывание А, а в третьей – высказывание B.

Переходим к четвёртому
столбцу. Здесь снова логическая операция – конъюнкция. А данные мы будем брать
из первого и третьего столбцов. И снова 1 будет стоять только в четвёртой
строке для данного столбца, так как оба наших высказывания – истинны. В
остальных – будут стоять нули.

Нам осталось заполнить
последний, пятый столбец. Логическая операция – дизъюнкция. Правило
звучит следующим образом: новое высказывание будет ложно тогда и только тогда,
когда ложны исходные высказывания. Рассматривать будем второй и четвёртый
столбцы. Значит в первой и третьей строках для данного столбца будут стоять
нули, так как оба выражения в данной ситуации ложны. В остальных строках этого
же столбца будут стоять единицы.

Мы построили таблицу
истинности для нашего логического выражения. Следует обратить внимание, что
данные в последнем столбце совпали с данными столбца B.
В такой ситуации говорят, что логическое выражение (A
& B) & A
V B
равносильно
логической переменной B.

А сейчас рассмотрим основные
свойства логических операций. Их называют законами алгебры логики.

1. Переместительный
(коммутативный) закон: при перестановки местами переменных в конъюнкции и
дизъюнкции значение выражения не изменяется.

A
& B = B & A.

A
V B = B V A.

Как мы знаем, конъюнкцию
называет логическим умножением, а дизъюнкцию – логическим сложением. Если наши
логические операции заменить соответствующими им арифметическими знаками, то мы
можем видеть, что при перестановке местами переменных в умножении и сложении,
значение выражения не изменяется.

A
· B
= B · A.

A
+ B = B
+ A.

2. Сочетательный
(ассоциативный) закон: если в выражении все операции одинаковы, например,
две конъюнкции, то скобки можно ставить произвольно или вообще опускать.

(A
& B) & C = A & (B & C).

(A
V B) V C = A V (B V C).

И снова если заменить
логические операции соответствующими арифметическими знаками, то мы можем
увидеть, где бы не стояли скобки, значение от этого не изменится, даже если
скобки вообще будут отсутствовать.

(A
· B) ·
C = A · (B ·
C);                            (A ·
B) · C = A ·
B · C.

(A
+ B) + C = A + (B + C);                       (A + B) + C = A + B + C.

3. Распределительный
(дистрибутивный) закон.

A
& (B V
C) = (A
& B) V
(A & C)

A
V (B & C) = (A V B) & (A V C)

И снова давайте заменим
логические операции арифметическими знаками. Рассмотрим сначала логическое
умножение. Получим:

A
· (B + C) = (A ·
B) + (A · C).

A
+ (B · C)
= (A + B)
·
(A + C).

Всё также, как и в
алгебре.

4. Закон двойного
отрицания: двойное отрицание исключает отрицание.

Если же говорить
математическим языком, то можно сказать, что минус на минус даёт плюс.

–
(– A) = A.

5. Закон исключённого
третьего.

       

Рассмотрим логическое
умножение.

То есть если А = 0, то Ā
= 1.

0 ·
1 = 0.

И наоборот, если А = 1,
то Ā = 0.

1 ·
0 = 0.

Перейдём к логическому
сложению.

Если А = 0, то Ā =
1.

0 + 1 = 1.

И наоборот, если А = 1,
то Ā = 0.

1 + 0 = 1.

Из этого можно сделать вывод:
из двух противоречивых высказываний об одном и том же предмете одно всегда истинно,
а второе – ложно, третьего не дано.

6. Закон повторения:
при конъюнкции или дизъюнкции одного и того же высказывания, получится это же
высказывание.

A
& A = А.

A
V A = А.

То есть:

A
· A
=
А;

A
+
A = А.

Давайте рассмотрим
логическое умножение. Например, если А = 0, то:

0 ·
0 = 0.

А если А = 1, то:

1 ·
1 = 1

При логическом сложении,
если А = 0, то:

0 + 0 =0.

Если же А = 1, то:

1 + 1 =1.

Алгебра логики оперирует
только двумя значениями: ложью (логический ноль) и истинной (логическая
единица). Истина не может быть двойной, тройной или истиной в квадрате, поэтому
при сложении двух истин результатом будет просто истина, то есть цифра 1.

7. Законы операций с 0
и 1.

Здесь всё просто.
Рассмотрим конъюнкцию.

При умножении любого
выражения на 0 мы всегда получим 0, а при умножении любого выражения на 1 –
всегда будем получать это же выражение.

A
& 0 = 0;           A · 0
= 0.

A
& 1 = A;          A
·
1 = А.

А если же рассматривать
дизъюнкцию, то при прибавлении к выражению 0 мы получим это же выражение. А вот
при прибавлении к выражению 1, в результате получим 1. Почему мы получаем
именно единицу, мы уже рассматривали с вами на примере прошлого закона.

A
V 0 = А;          A
+ 0 = A.

A
V 1 = 1;           A
+
1 = 1.

8. Закон общей
инверсии. Для того, чтобы найти инверсию конъюнкции, нужно найти дизъюнкцию
инверсий каждого логического выражения. Для того, чтобы найти инверсию
дизъюнкции, нужно найти конъюнкцию инверсий каждого логического выражения.

         

Все законы алгебры логики
можно доказать с помощью таблиц истинности.

Давайте докажем закон
общей инверсии для логического умножения.

Построим таблицу. У нас 2
переменных в выражении. Число логических операций равно 5. Значит число
столбцов будет равно 7.

Теперь установим
последовательность выполнения логических операций. Для начала будем брать
выражение слева от равно. Значит в первую очередь будет выполняться конъюнкция,
а затем инверсия.

Справа от равно будет
сначала выполняться инверсия А, затем инверсия B
и после этого – дизъюнкция получившихся выражений.

Зададим названия для
наших столбцов в соответствии с порядком выполнения операций.

Количество строк будет
равно 4 (шапка таблицы сюда не входит), так как:

2²
= 4.

Теперь выпишем наборы
входных переменных. Это будут числа от 0 до 3. Представим их в двухразрядном
коде и получим следующие числа:

0₁₀
= 00₂

1₁₀
= 01₂

2₁₀
= 10₂

3₁₀
= 11₂

Заполним таблицу.

Теперь перейдём
непосредственно к логическим операциям. Первая – конъюнкция А и B.
Новое высказывание будет истинно тогда и только тогда, когда истинны исходные
высказывания. Значит единица будет стоять в последней строке для данного
столбца, а во всех остальных – нули.

Следующая операция –
инверсия. Если исходное высказывание было истинно, то после инверсии оно
становится ложным, а если исходное высказывание было ложным, то после операции
инверсии оно становится истинным. Значит если у нас единица, то она будет
заменена на ноль, а если ноль, то на единицу. Заполним четвёртый столбец,
исходя из данных, которые находятся в третьем столбце.

Мы получили результат
выражения, которое находится слева от равно. Обведём наш столбец. Он нам
понадобится в дальнейшем.

Идём дальше. Пятый
столбец – инверсия А. И снова, если исходное выражение равно единице, то оно
станет равно нулю и наоборот. Заполним столбец цифрами, исходя из данных,
которые находятся в первом.

Аналогично заполним
шестой столбец. Только опираться мы будем на второй.

Последняя операция –
дизъюнкция. Новое высказывание будет ложно тогда и только тогда, когда ложны
исходные высказывания. Значит 0 будет стоять в последней строке для данного
столбца, а во всех остальных – единицы.

Мы получили результат
выражения, которое стоит справа от равно. Также обведём его.

Давайте посмотрим на
выделенные столбцы. Их значения совпадают. Это и доказывает справедливость
закона общей инверсии.

Давайте найдём значение
логического выражения: (D
> 1) V (D
< 2). Число D
= 1.

Переходим к решению. D
= 1 получим следующее:

Логическое выражение «1 >
1» не верно. Заменим его 0. Выражение «1 < 2» – верно, поэтому заменим его 1.
Получим:

И это будет равно:

Вернёмся к закону
повторения. Согласно этому закону, значение данного логического выражения равно
нулю. Таким образом значение нашего логического выражения, при D
= 1, равно 0.

А сейчас подведём итоги
нашего урока. Сегодня мы познакомились с правилами построения таблиц истинности
для логического выражения. Научились строить таблицу истинности для логического
выражения на примере. Также узнали, какие существуют законы алгебры логики и с
помощью таблицы истинности доказали достоверность одного из них.

Необходимо построить таблицу истинности.

Будем действовать согласно приведённому выше алгоритму.

1. Количество переменных — (3) (X, Y, Z); количество логических операций — (3).

2. Построим таблицу. Заполним шапку таблицы сначала переменными, а потом логическими операциями. Первое действие в скобках, второе — отрицание, третье — конъюнкция.

3. Перечислим все возможные значения входных данных. Для того чтобы не пропустить ни одного значения, используют следующее правило: в значение первой переменной записывают (4) нуля, затем (4) единицы, в значении второй переменной чередуют (2) нуля и (2) единицы, а значение третьей переменной — чередование (0) и (1).

4. Заполним ячейки таблицы, выполняя логические операции.

План урока:

Способы решению задач по логике

Табличный способ – этапы, особенности

Сравнение методов решения

Построение таблиц истинности для различных типов задач

Построение электрических схем, реализующих логические операции

Способы решения задач по логике

Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:

• рассуждая над условием;
• решая логические операции;
• используя таблицы истинности.

Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.

Этапы решения логических задач:

• Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
• Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
• Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
• Проверить, соответствует ли полученный результат условию задачи.

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

• Определить число логических значений/переменных (n) в примере.
• Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
• Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
• Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
• Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2ⁿ+ 1 (шапка).
• Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
• Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
• Сделать выводы на основании полученных результатов.

Если необходимо перебрать все значения простых выражений, то для задач:

• с 2-мя переменными может быть только 4 набора логических переменных;

Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.

 Обязательно учитывают приоритет операций:

• Указанные в скобках.
• Отрицание.
• Логическая конъюнкция чисел.
• Дизъюнкция.
• Строгая дизъюнкция.
• Импликация.
• Эквивалентность.

Обозначение логических операций:

Сравнение методов решения

Метод рассуждений

Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.

Пример №1.

Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.

Известно, что:

• дом плотника правее егеря;
• стоматолог проживает левее егеря;
• дом гитариста с самого краю;
• стоматолог живет рядом с гитаристом;
• Владимир не гитарист, и его дом не соседствует с гитаристом;
• дома Дмитрия и егеря соседние;
• здание, в котором прописан Андрей, правее стоматолога;
• между домами Андрея и Дмитрия один дом.

Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:

Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:

Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.

Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.

Такой подход лучше не использовать, если условие сложное или много данных.

Табличный метод

Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).

Чтобы построить таблицу истинности логических выражений, следует:

• Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
• Записать условие задачи, как составное выражение из символов логических операций.
• Нарисовать таблицу истинности для полученных данных.
• Выбрать такой вариант, при котором полученные значения подходят под условие.
• Проверить соответствие выбранного варианта и условия задачи.

Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:

Рассмотрим тот же пример.

Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:

Метод компактнее, для некоторых задач нагляднее.

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

• Если А получит максимальный бал, то максимальный бал получат Ви С.
• А и С получат или не получат максимальный бал одновременно.
• Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

• последняя – гласная (Х1);
• или первая буква согласная (Х2)
• вторая – согласная (Х3).

¬(Х1→Х2)VХ3

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

 Построение электронных схем, реализующих логические операции

Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.

Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.

Электросхема с конъюнктором

 Рассмотрим все варианты:

• Все контакты включены, тогда источник света горит.
• Первый контакт в положении «выключено» – свет не горит.
• Второй контакт выключен – лампа не светит.
• Все контакты отключены – свет не горит.

Заключение – эта электрическая цепь реализует операцию «И».

Дизъюнктор, схема электропитания

Рассмотрим этот вид электрической цепочки:

• Все контакты включены – лампа горит.
• Первый контакт включен, второй выключен – свет горит.
• Обратная ситуация – выключен первый, включен второй – лампа светится.
• Все контакты выключены – света нет.

Заключение – такой вид электросхем соответствует логической операции «ИЛИ».

Инвертор в электросхемах

В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.

Заключение: схема соответствует логической операции «НЕ».

Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.

Обозначение логических элементов

Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.

Построение таблиц истинности

Екатерина Андреевна Гапонько

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Определение 1

Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.

Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.

Определение 2

Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.

Определение 3

Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:

Рисунок 1.

Приоритетом в выполнении порядка выполнения операций пользуются скобки.

Алгоритм построения таблицы истинности логической функции

1. Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.

2. Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.

3. Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.

«Построение таблиц истинности» 👇

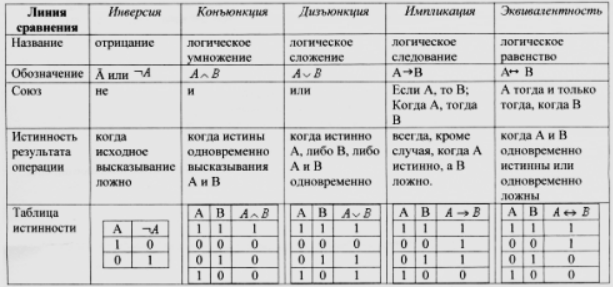
Рисунок 2.

Пример 1

Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.

Решение:

1. Определим количество строк:

   Количество простых выражений – $n=3$, значит

   кол-во строк = $2^3 + 1=9$.

2. Определим количество столбцов:

   Количество переменных – $3$.

   Количество логических операций и их последовательность:

   1. инверсия ($bar{A}$);
   2. дизъюнкция, т.к. она находится в скобках ($B vee C$);

   3. дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.

      Кол-во столбцов = $3 + 3=6$.

3. Заполним таблицу, учитывая таблицы истинности логических операций.

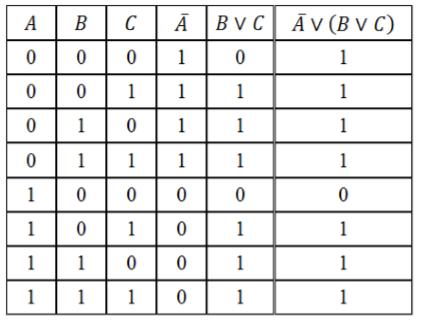
Рисунок 3.

Пример 2

По данному логическому выражению построить таблицу истинности:

[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]

Решение:

1. Определим количество строк:

   Количество простых выражений – $n=3$, значит

   кол-во строк = $2^3 + 1=9$.

2. Определим количество столбцов:

   Количество переменных – $3$.

   Количество логических операций и их последовательность:

   1. отрицание ($bar{C}$);
   2. дизъюнкция, т.к. она находится в скобках ($A vee B$);
   3. конъюнкция ($(Avee B)bigwedge overline{C}$);
   4. отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
   5. дизъюнкция ($A vee C$);
   6. конъюнкция ($(Avee C)bigwedge B$);
   7. отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);

   8. дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).

      Кол-во столбцов = $3 + 8 = 11$.

3. Заполним таблицу, учитывая таблицу истинности логических операций.

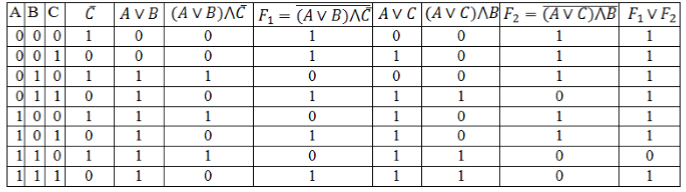
Рисунок 4.

Алгоритм построения логической функции по ее таблице истинности

1. Выделяют в таблице истинности строки со значением функции, равным $1$.
2. Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
3. Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
4. В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.

Пример 3

По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.

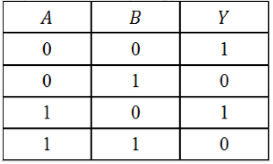
Рисунок 5.

Решение:

1. Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
2. Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:

   

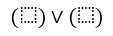
   Рисунок 6.

3. Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
4. В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата написания статьи: 12.04.2016

Цели урока: SMART цель сравнить способы заполнения таблиц истинности, выявить закономерности их заполнения.

Обучающие:

• Повторить основные понятия логики;
• Ввести понятие “таблица истинности”;
• Изучить последовательность действий построения таблиц истинности;
• показать  нахождение значения логических выражений посредством построения таблиц истинности;
• Ввести понятие равносильности логических выражений.

Развивающие:

• Развивать логическое мышление;
• Развивать внимание;
• Развивать память;
• Развивать речь учащихся.

Воспитательные:

• Воспитывать умение слушать учителя и одноклассников;
• Воспитывать дисциплинированность;
• Формировать интеллектуальную и эмоциональную активность учащихся;
• Воспитывать чувства ответственности за результаты своего труда.

Задачи урока:

• вспомнить принцип работы основных логических элементов;
• запомнить порядок выполнения логических операций в сложном логическом выражении;
• обратить внимание на закономерность внесения исходных данных в таблицу, сравнить их с числами разных систем счисления;
• найти с помощью таблицы истинности значения двух логических функций.

Вид урока: комбинированный.

Тип урока: проверка знаний и изучение нового материала.

Методы организации учебной деятельности: фронтальная, групповая.

Система оценивания: проверка в парах.

Оборудование урока: Презентация урока, плакаты «Таблица истинности функции логического сложения», «Таблица истинности функции логического умножения», «Таблица истинности функции логического отрицания», «Оценочный лист»,
карточки с заданиями, мультимедийный проектор.

Приложение 1

Место проведения урока: компьютерный класс.

Участники: ученики 8 Б класса.

Ход урока

 I. Организационный момент (2 минуты)

СЛ1. На экране проецируется первый слайд презентации – надпись «Таблицы истинности».

– Здравствуйте, ребята. Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Таблицы истинности». Я расскажу вам как можно определить истинность сложных высказываний посредством составления таблиц истинности.

СЛ2. Цель урока: сравнить способы заполнения таблиц истинности, выявить закономерности их заполнения.

СЛ3. Ребята, какие задачи нам надо решить чтобы достигнуть этой цели?

1. Повторить что называется высказыванием.
2. Что называется логической переменной.
3. Познакомиться с определением таблицы истинности.
4. Рассмотреть правила составления таблиц истинности.
5. Узнать приоритеты логических операций (сравнить их с порядком выполнения
   математических операций).
6. Внимательно разобрать 2 примера заполнения таблиц истинности.

СЛ4. Эпиграфом к уроку являются слова Б.Паскаля: “ВЕЛИЧИЕ ЧЕЛОВЕКА – В ЕГО СПОСОБНОСТИ МЫСЛИТЬ”.
 
Сегодня на уроке мы с вами должны мыслить и рассуждать вместе.

II. Повторение

СЛ5.

1. Что такое логика?

Логика – это наука о формах и способах  мышления, это учение о способах рассуждений и доказательств.

2. Что такое алгебра логики?

Алгебра логики это наука об общих операциях аналогичных сложению и умножению, которые выполняются не только над числами, но и над другими математическими объектами, в том числе и над высказываниями.

3. Что называется высказыванием в алгебре логики?

Высказывание – это повествовательное предложение, в котором что-либо утверждается или отрицается.

Можно сказать истинно оно или ложно.

Истинным будет высказывание в котором связь понятий правильно отражает свойства и отношения реальных вещей.

Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.

4. Что называется логической переменной?

Логическая переменная – простое высказывание, содержащее только одну мысль.

Её символически обозначают латинскими буквами А, В, С.

Значения логической переменной могут быть только константы истина и ложь (1 и 0).

5. Что называют логической функцией?

Логическая функция это составное высказывание, которое содержит несколько простых мыслей, соединённых между собой с помощью логических операций.
 
6. Сколько основных логических операций существует? (три)

Давайте вспомним принцип их работы.

III. Самостоятельная работа

У вас на столах лежат листочки с самостоятельной работой.

СЛ6.

1. Подпишите листочек.
2. Заполните пропуски в таблицах истинности.
3. Проверить работу друг друга и поставить оценку.

Что было сложным в этой работе? Какие у вас возникли затруднения?

IV. Проверка самостоятельной работы

СЛ7.

1. Какой логической функции соответствует данная таблица истинности?

A	B	A?B
0	0	0
0	1	0
1	0	0
1	1	1

1. Конъюнкция
2. Дизъюнкция
3. Отрицание

Как называется эта функция по другому?

СЛ8.

2. Какой логической функции соответствует данная таблица истинности?

A	B	A?B
0	0	0
0	1	1
1	0	1
1	1	1

1. Конъюнкция
2. Дизъюнкция
3. Отрицание

Как называется эта функция по другому?

СЛ9.

3. Какой логической функции соответствует данная таблица истинности?

1. Конъюнкция
2. Дизъюнкция
3. Отрицание

Как называется эта функция по другому?

III. Объяснение нового материала

В математике функция принимает множество значений. А в логике только два значения 0 или 1.

Знаете ли вы кто является основателем двоичной системы счисления?

Правильно, Готфрид Вильгельм Лейбниц – немецкий ученый (философ, математик, физик, языковед)

СЛ 10. В своей бинарной арифметике Лейбниц видел прообраз творения: «Двоичная математика-прообраз творения.

1 представляет собой божественное начало, а 0 – небытие и высшее существо создаёт всё сущее из небытия точно таким же образом как 0 и 1 в двоичной системе выражают все числа.»

Итак: Логическая функция – это функция, в которой переменные принимают только два значения: логическая единица или логический ноль.

При знакомстве с принципом работы основных логических операций мы видели таблицы, которые отражали принцип работы этих элементов, мы называли их таблицами истинности. Какие таблицы можно называть таблицами истинности? Сейчас мы запишем определение в тетрадь.

СЛ11. Таблицу, показывающую, какие значения принимает сложное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний называют таблицей истинности сложных высказываний.

Запишем определение в тетрадь.

СЛ12. При построении таблиц истинности есть определенная последовательность действий.

Перед нами Алгоритм построения таблицы истинности.

Я распечатала его на листочках, чтобы вы вклеили их  в тетрадь Итак первый шаг.

1. Подсчитать количество переменных n в формуле 2³.

2. Определить количество строк в таблице истинности m = 2ⁿ.

3. Подсчитать количество логических операций в формуле.

4. Установить последовательность выполнения логических операций с учётом
скобок и приоритетов.

5. Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

6. Выписать наборы входных переменных с учётом того, что они представляют собой натуральный ряд n разрядных двоичных чисел от 0 до 2ⁿ–1.

7. Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

СЛ 13. Рассмотрим пример.

Построить таблицу истинности для A ˄ (B ˅ В ˄ С)
 
Записали в тетрадь. Для построения таблицы истинности.

1  Определить количество строк в таблице.

Как мы это делаем?

Считаем количество переменных. В нашем случае логическая функция содержит 3 переменные.

Какие? А и В и C.

Значит сколько строк будет в таблице?

Количество строк в таблице истинности должно быть равно 2³ = 8.

Верно. Что делаем дальше?

2. Определяем количество столбцов = количеству логических переменных плюс количество логических операций.

3. Сколько будет в нашем случае операций?

В нашем случае количество переменных равно трём, а количество логических операции – пяти, то есть количество столбцов таблицы истинности равно 8.

Хорошо. Дальше?

Строим таблицу 8 столбцов, 9 строк (учитываем заголовок таблицы).

СЛ 14. Порядок операций определяется по аналогии с математикой.

Запишите в тетрадь.

(Мы сначала возводим в степень, затем выполняем операции в скобках, потом делаем умножение деление слева направо как видим их и в последнюю очередь сложение, умножение.

• отрицание
• конъюнкция
• дизъюнкция
• импликация
• эквивалентность

Какую операцию будем выполнять первой? Только учитывайте скобки и приоритеты, сначала необходимо выполнить логическое отрицание переменной В, а затем переменной С.

Сначала необходимо выполнить операции в скобках:
найдём значение логического умножения, а  затем логическое сложение.

В последнюю очередь выполним операцию конъюнкции

СЛ 15. Расставим порядок операций в нашем выражении.

СЛ 17. Наборы входных переменных можно заполнять по следующему правилу.

а) определить количество наборов входных переменных(если 3 переменных значит 3 набора 4 переменные 4 набора);

б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю —1;

в) разделить колонку значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0;

г) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.

СЛ18. Заполним наборы входных переменных.

Разделим 1 колонку значений первой переменной пополам и заполним верхнюю часть колонки 0, а нижнюю 1.

СЛ19. Вторую колонку делим на 4 части и заполняем каждую по очереди единицами и нулями.

СЛ20. Третью колонку делим на 8 частей и в каждой клетке пишем по очереди 1 и 0.

Мы получили наборы значений исходных логических переменных с учётом того, что они представляют собой натуральный ряд 3-разрядных двоичных чисел от 0 до 7.

(Мы недавно изучали системы счисления, и работали с 8-ричной ПСС. Вы знаете, что каждое число 8-ричной ПСС можно представить триадой двоичных эквивалентов) вот перед вами числа от 1 до 7 представленные в восьмеричной системе счисления.

Заполняем таблицу истинности по столбцам. Начинаем:

СЛ21. Выполняем отрицание переменной В.

СЛ22. Выполняем отрицание переменной С.

СЛ23. Выполняем конъюнкцию двух отрицаний.

СЛ24. Выполним логическое сложение конъюнкции и переменной В.

Чтобы сконцентрировать своё внимание на нужных столбцах давайте пометим их снежинкой Обратите внимание другим цветом я выделила те значения в результирующем столбце которые встречаются реже.

СЛ25. А теперь выполняем последнюю операцию конъюнкцию (нужные столбцы я пометила восклицательным знаком.

В последнем столбце и находится значение нашего выражения.

Мы познакомились с первым способом заполнения таблиц истинности.

СЛ26. Если количество переменных небольшое можно использовать другой способ заполнения таблицы истинности.

Пример. Составьте таблицу истинности для выражения: (X1&X2) ˅ ( X1˅X2).

Идея заключается в том, что данную формулу нужно растянуть по горизонтали на страницу тетради так, чтобы под каждой переменной и каждой операцией осталось место для столбца значений.

Под формулой( подпишем столбцы возможных значений под каждой из переменных Х1 и Х2 последовательно (по приоритету операций) выпишем столбцы значений операций.

(Х1	&	X2)	˅	(	X1	˅	X2)
0	0	0	1	1	0	1	0
0	0	1	1	1	0	1
1	0	0	0	0	1	0	0
1	1	1	1	0	1	1	1

СЛ26.  Заполняем значения переменных.

СЛ27. Выполняем первую операцию  конъюнкции в скобочках.

СЛ27. Выполняем отрицание переменной Х1.

СЛ28. Выполняем операцию дизъюнкции в скобках.

СЛ29. Выполняем последнюю операцию дизъюнкции, которая стоит между скобками.

Ребята, какой способ вам понравился больше

Какой легче выполнять?

СЛ30.

IV. Домашнее задание

1. Построить таблицы истинности для следующих выражений:

а) А ˅ (В ˅ В)

б) А ˄ (В ˄ В ˅ С)

*в) А ˅(В ˅ В) ˄ А ˄ (В → С)

Кто желает получить дополнительную оценку делает задание со снежинкой

СЛ31.

V. Итог урока

– Вы познакомились с новым способом решения логических задач – с помощью таблиц истинности.

Ребята, выполнили мы сегодня на уроке поставленные нами задачи?

Достигли цель урока?

Рефлексия

• сегодня я узнал…
• было интересно…
• было трудно…
• я выполнял задания…
• я понял, что…
• теперь я могу…
• я почувствовал, что…
• я приобрел…
• я научился…
• у меня получилось

Урок окончен, спасибо за работу.