Таблица как найти скорость время расстояние формулы

Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.

Расстояние

Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).

Расстояние связано со скоростью и временем:

S=v cdot t

Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.

Единицы длины	СИ
1 сантиметр	0,01 м
1 километр	1000 м
1 дециметр	0,1 м
1 миллиметр	0,001 м
1 микрометр	1·10-6 м
1 миля	1609,34 м
1 фут	0,3048 м
1 ярд	0,9144 м
1 дюйм	0,0254 м
1 морская миля	1852 м

Время

Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.

Время можно найти по формуле:

t=frac{S}{v}

Скорость

Скорость обозначается буквой  — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.

Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.

Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.

Формула скорости

Скорость можно найти через расстояние и время по формуле:

v=frac{S}{t}

Средняя скорость

Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.

Формула средней скорости:

v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}

То есть средняя скорость это отношение всего пути, ко всему времени.

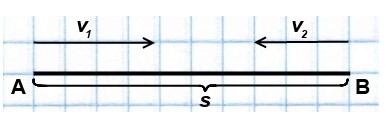
Скорости сближения и удаления

Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.

Скорость удаления

Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.

Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:

3+4=7 км/ч.

Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.

Формула скорости удаления:

v_{удаления}=v_1+v_2

где — скорость одного тела,

— скорость другого тела.

Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.

Скорость сближения двух тел

Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.

Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.

Формула скорости сближения:

v_{сближения}=v_1+v_2

где  — скорость одного тела,

 — скорость другого тела.

Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.

То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (=5 км/ч), то скорость их сближения будет 2 км/ч:

Формула скорости сближения при движении вдогонку:

v_{сближения}=v_1-v_2

где  — скорость одного тела,

 — скорость другого тела. При этом

Таблица «скорость, время, расстояние» при решении задач на движение

При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.

Скорость, v, м/с

Время, t, с

Расстояние, S, м

Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.

Составляем таблицу и записываем в нее данные:

Скорость, v, км/ч	Время, t, ч	Расстояние, S, км
?	5	45

Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.

Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))

Рассмотрим теперь некоторые примеры решения задач

Примеры задач на движение

Задача 1

Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?

Решение:

Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.

Школьник дойдет до дома за полчаса.

Ответ: 0,5 ч.

Задача 2

Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?

Решение: Составим таблицу

	Скорость, v, км/ч	Время, t, ч	Расстояние, S, км
Автомобилист	50	100/50	100
Велосипедист	x	100/x	100

Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:

displaystyle frac{100}{x}-frac{100}{50}=8

Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.

Решим полученное уравнение.

displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10

Ответ: 10 км/ч

Задача 3

Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.

Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.

В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:

0,05 cdot 60=3 c.

Тогда displaystyle v= frac{180}{3}=60 м/с.

Ответ: 60 м/с

Задача 4

Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?

Решение:

Определим весь путь который прошел турист:

displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.

Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч

Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч

Тогда найдем среднюю скорость:

displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.

Ответ: displaystyle v_{ср}=4 frac{2}{7}

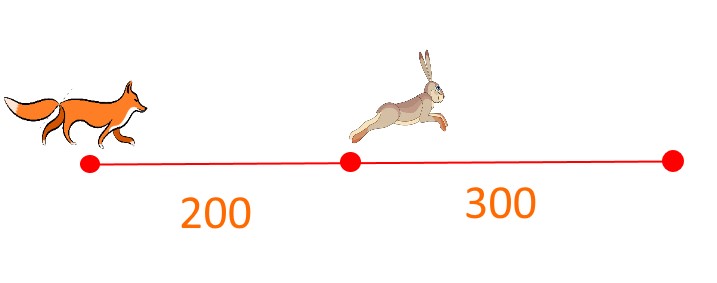
Задача 5

Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?

Решение:

Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.

Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.

Лиса не догонит зайца.

Действительно, скорость сближения лисы и зайца:

displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с

То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с

Заяц же уже 20 секунд будет в безопасном месте.

Ответ: лиса зайца не догонит.

Памятка “СКОРОСТЬ. ВРЕМЯ. РАССТОЯНИЕ.”

Памятка

по математике 4 класс по теме

«Скорость, время, расстояние»

S – расстояние ( путь); измеряется в км, м и т.д.

V – скорость ( это расстояние, преодолеваемое за единицу времени); измеряется в км/ч, м/ мин и т.д.

t- время; измеряется в часах, минутах и т.д.

1. Чтобы найти расстояние, нужно скорость умножить на время. S =V х t
2. Чтобы найти скорость, нужно расстояние разделить на время.

V = S : t

1. Чтобы найти время, нужно расстояние разделить на скорость.

t = S :V

Задача на нахождение расстояния

Пешеход шёл со скоростью 5 километров в час. Какой путь он пройдёт за 3 часа?

5  х 3 = 15 ( км)

Ответ: 15 километров пройдёт пешеход.

Задача  на нахождение скорости

Пешеход за 3 часа прошёл 15 километров. С какой скоростью шёл пешеход?

15 : 3 = 5 ( км/ч)

Ответ: 5 км/ ч скорость пешехода.

Задача на нахождение времени

Пешеход шёл со скоростью 5 километров в час и прошёл 15 километров. Сколько времени шёл пешеход?

15 : 5 = 3 ( ч)

Ответ: 3 часа шёл пешеход.

Таблица в помощь четверокласснику для решения задач на движение “Скорость. Время. Расстояние”.

S – расстояние;

t – время;

V – скорость.

Единицы измерения: км., м., см., дм.,мм.

For candidates appearing in competitive exams, mastering quantitative aptitude topics such as Speed, Time, and Distance is crucial. From calculating average speeds to solving complex distance-time problems, candidates must be prepared for a variety of questions that test their speed, time, and distance skills.

To help you stay ahead in the competition, this article provides an overview of the concepts and formulas related to these topics as well as some useful tricks, sample questions, and answers to help candidates prepare for this essential topic.

If you are preparing for competitive exams, it is essential to have a clear understanding of the quantitative aptitude syllabus and the topics covered in it. To help you navigate this crucial subject, we have compiled a comprehensive guide that covers the key topics and concepts related to quantitative aptitude.

Practice Quiz :

Practice Speed, Time and Distance Aptitude Quiz Questions

Speed, Time, and Distance Concepts

Speed, distance, and time are essential concepts of mathematics that are used in calculating rates and distances. This is one area every student preparing for competitive exams should be familiar with, as questions concerning motion in a straight line, circular motion, boats and streams, races, clocks, etc. often require knowledge of the relationship between speed, time, and distance. Understanding these inter-relationships will help aspirants interpret these questions accurately during the exams.

Units of Speed, Time, and Distance

The most commonly used units of speed, time, and distance are:

• Speed: kilometers per hour (km/h), meters per second (m/s), miles per hour (mph), feet per second (ft/s).
• Time: seconds (s), minutes (min), hours (h), days (d).
• Distance: kilometers (km), meters (m), miles (mi), feet (ft).

For example, to convert km/h to m/s, multiply by 5/18, and to convert m/s to km/h, multiply by 18/5. 

Being familiar with these units and their conversions can help in solving quantitative aptitude questions related to speed, time, and distance efficiently.

Relationship Between Speed, Time & Distance

Understanding the relationship between speed, time, and distance is essential to solve problems.

Speed, Time, and Distance 

• Speed = Distance/Time

The speed of an object describes how fast or slow it moves and is calculated as distance divided by time.

Speed is directly proportional to distance and inversely proportional to time.

• Distance = Speed X Time

The distance an object travels is directly proportional to its speed – the faster it moves, the greater the distance covered.

• Time = Distance / Speed

Time is inversely proportional to speed – the faster an object moves, the less time it takes to cover a certain distance.
As speed increases, time taken decreases, and vice versa

Speed, Time, and Distance Formulas 

Some important speed, distance, and time formulas are given in the table below:-

TERMS	FORMULAS
SPEED	SPEED= DISTANCE/TIME
DISTANCE	DISTANCE= SPEED × TIME
TIME	TIME= DISTANCE/SPEED
AVERAGE SPEED	AVERAGE SPEED= TOTAL DISTANCE TRAVELLED/TOTAL TIME TAKEN
AVERAGE SPEED (WHEN DISTANCE IS CONSTANT)	2xy/xy
RELATIVE SPEED (IF TWO TRAINS ARE MOVING IN OPPOSITE DIRECTIONS )	RELATIVE SPEED=X+Y TIME TAKEN= L1 + L2/X+Y HERE L1 AND L2 ARE LENGTHS OF TRAINS
RELATIVE SPEED (IF TWO TRAINS ARE MOVING IN SAME DIRECTION)	RELATIVE SPEED=X-Y TIME TAKEN= L1 + L2/X-Y HERE L1 AND L2 ARE LENGTHS OF TRAINS

Speed, Time, and Distance Conversions

The Speed, Time, and Distance Conversions into various units is important to understand for solving problems:-

• To convert from km/hour to m / sec: a Km/hr = a x (5/18) m/s
• To convert from m / sec to km/hour: a m/s = a x (18/5) Km/hr
• If a person travels from point A to point B at a speed of S kilometers per hour (kmph) and returns back from point B to point A at a speed of S2 kmph, the total time taken for the round trip will be T hours. Distance between points A and B = T (S1S2/(S1+S2)).
• If two moving trains, one of length l1 traveling at speed S2 and the other of length l2 going at speed S2, intersect each other in a period of time t. Then their Total Velocity can be expressed as S1+S2 = (l1+l2)/t.
• When two trains pass each other, the speed differential between them can be determined using the equation S1-S2 = (l1+l2)/t, where S1 is the faster train’s speed, S2 is the slower train’s speed, l1 is the faster train’s length and l2 is the slower train’s length, and t is the time it takes for them to pass each other.
• If a train of length l1 is travelling at speed S1, it can cross a platform, bridge or tunnel of length l2 in time t, then the speed is expressed as  S1 = (l1+l2)/t
• If the train needs to pass a pole, pillar, or flag post while travelling at speed S, then S = l/t.
• If two people A and B both start from separate points P and Q at the same time and after crossing each other they take T1 and T2 hours respectively, then (A’s speed) / (B’s speed) = √T2 / √T1 

Applications of Speed, Time, and Distance

Average Speed = Total Distance Traveled/Total Time Taken

Case 1: when the same distance is covered at two separate speeds, x and y, then Average Speed is determined as 2xy/x+y.

Case 2: when two speeds are used over the same period of time, then Average Speed is calculated as (x + y)/2.

Relative speed: The rate at which two moving bodies are separating from or coming closer to each other. 

Case 1: If two objects are moving in opposite directions, then their relative speed would be S1 + S2

Case 2: If they were moving in the same direction, their relative speed would be S1 – S2

Inverse Proportionality of Speed & Time: When Distance is kept constant, Speed and Time are inversely proportional to each other. 

This relation can be mathematically expressed as S = D/T where S (Speed), D (Distance) and T (Time). 

To solve problems based on this relationship, two methods are used:

1. Inverse Proportionality Rule
2. Constant Product Rule.

Sample Problems on Speed, Time, and Distance

Q1: A runner can complete a 750 m race in two and a half minutes. Will he be able to beat another runner who runs at 17.95 km/hr? 

Solution: 

We are given that the first runner can complete a 750 m race in 2 minutes and 30 seconds or 150 seconds. 
=> Speed of the first runner = 750 / 150 = 5 m / sec 
We convert this speed to km/hr by multiplying it by 18/5. 
=> Speed of the first runner = 18 km / hr 
Also, we are given that the speed of the second runner is 17.95 km/hr. 
Therefore, the first runner can beat the second runner. 

Q2: A man decided to cover a distance of 6 km in 84 minutes. He decided to cover two-thirds of the distance at 4 km/hr and the remaining at some different speed. Find the speed after the two-third distance has been covered. 

Solution: 

We are given that two-thirds of the 6 km was covered at 4 km/hr. 
=> 4 km distance was covered at 4 km/hr. 
=> Time taken to cover 4 km = 4 km / 4 km / hr = 1 hr = 60 minutes 
=> Time left = 84 – 60 = 24 minutes 
Now, the man has to cover the remaining 2 km in 24 minutes or 24 / 60 = 0.4 hours 
=> Speed required for remaining 2 km = 2 km / 0.4 hr = 5 km / hr 

Q3: A postman traveled from his post office to a village in order to distribute mail. He started on his bicycle from the post office at a speed of 25 km/hr. But, when he was about to return, a thief stole his bicycle. As a result, he had to walk back to the post office on foot at the speed of 4 km/hr. If the traveling part of his day lasted for 2 hours and 54 minutes, find the distance between the post office and the village. 

Solution : 

Let the time taken by postman to travel from post office to village=t minutes. 
According to the given situation, distance from post office to village, say d1=25/60*t km {25 km/hr = 25/60 km/minutes} 
And 
distance from village to post office, say d2=4/60*(174-t) km {2 hours 54 minutes = 174 minutes} 
Since distance between village and post office will always remain same i.e. d1 = d2 
=> 25/60*t = 4/60*(174-t) => t = 24 minutes. 
=> Distance between post office and village = speed*time =>25/60*24 = 10km 

Q4: Walking at the speed of 5 km/hr from his home, a geek misses his train by 7 minutes. Had he walked 1 km/hr faster, he would have reached the station 5 minutes before the actual departure time of the train. Find the distance between his home and the station. 

Solution: 

Let the distance between his home and the station be ‘d’ km. 
=> Time required to reach the station at 5 km / hr = d/5 hours 
=> Time required to reach the station at 6 km/hr = d/6 hours 
Now, the difference between these times is 12 minutes = 0.2 hours. (7 minutes late – 5 minutes early = (7) – (-5) = 12 minutes) 
Therefore, (d / 5) – (d / 6) = 0.2 
=> d / 30 = 0.2 
=> d = 6 
Thus, the distance between his home and the station is 6 km. 

Q5 : Two stations B and M are 465 km distant. A train starts from B towards M at 10 AM with a speed of 65 km/hr. Another train leaves from M towards B at 11 AM at a speed of 35 km/hr. Find the time when both trains meet. 

Solution: 

The train leaving from B leaves an hour early than the train that leaves from M. 
=> Distance covered by train leaving from B = 65 km / hr x 1 hr = 65 km 
Distance left = 465 – 65 = 400 km 
Now, the train from M also gets moving and both are moving towards each other. 
Applying the formula for relative speed, 
Relative speed = 65 + 35 = 100 km / hr 
=> Time required by the trains to meet = 400 km / 100 km / hr = 4 hours 
Thus, the trains meet at 4 hours after 11 AM, i.e., 3 PM. 

Q6: A policeman sighted a robber from a distance of 300 m. The robber also noticed the policeman and started running at 8 km/hr. The policeman also started running after him at the speed of 10 km/hr. Find the distance that the robber would run before being caught. 

Solution: 

Since both are running in the same direction, relative speed = 10 – 8 = 2 km/hr 
Now, to catch the robber if he were stagnant, the policeman would have to run 300 m. But since both are moving, the policeman needs to finish off this separation of 300 m. 
=> 300 m (or 0.3 km)is to be covered at the relative speed of 2 km/hr. 
=> Time taken = 0.3 / 2 = 0.15 hours 
Therefore, distance run by robber before being caught = Distance run in 0.15 hours 
=> Distance run by the robber = 8 x 0.15 = 1.2 km 

  Another Solution : 
Time of running for both the policeman and the robber is same. 
We know that Distance = Speed x Time 
=> Time = Distance / Speed 
Let the distance run by the robber be ‘x’ km at the speed of 8 km / hr. 
=> Distance run by policeman at the speed of 10 km / hr = x + 0.3 
Therefore, x / 8 = (x + 0.3) / 10 
=> 10 x = 8 (x + 0.3) 
=> 10 x = 8 x + 2.4 
=> 2 x = 2.4 
=> x = 1.2 
Therefore, Distance run by the robber before getting caught = 1.2 km 

Q7: To cover a certain distance, a geek had two options, either to ride a horse or to walk. If he walked one side and rode back the other side, it would have taken 4 hours. If he had walked both ways, it would have taken 6 hours. How much time will he take if he rode the horse both ways? 

Solution : 

Time taken to walk one side + Time taken to ride one side = 4 hours 
Time taken to walk both sides = 2 x Time taken to walk one side = 6 hours 
=> Time taken to walk one side = 3 hours 
Therefore, time taken to ride one side = 4 – 3 = 1 hour 
Thus, time taken to ride both sides = 2 x 1 = 2 hours 

FAQs on Speed, Time, and Distance

Q1. What is speed, time, and distance?

Answer: 

Speed, time and distance are the three major concepts in physics. Speed is the rate of motion of an object between two points over a particular period of time which is measured in metres per second (m/s). Time is calculated by reading a clock, and it is a scalar quantity that do not change with direction. Distance is the total amount of ground covered by an object.

Q2. What is the average speed?

Answer: 

The formula for speed, time and distance is a calculation of the total distance an object travels over a given amount of time. It is a scalar quantity, meaning it’s an absolute value with no direction. To calculate it, you need to divide the total distance traveled by the amount of time it took to cover that distance.

Q3. What is the formula of speed, distance, and time?

Answer: 

• Speed = Distance/Time
• Time = Distance/Speed
• Distance = Speed x Time

Q4. What is the relationship between speed, distance, and time?

Answer: 

The relationship is given as follows:

• Distance = Speed x Time

Related Articles:

Problem on Time Speed and Distance | Set-2

Test your knowledge of Speed, Time and Distance in Quantitative Aptitude with the quiz linked below, containing numerous practice questions to help you master the topic:-

<< Practice Speed, Time and Distance Aptitude Questions >>