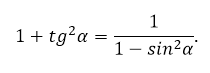Вы здесь
-
Таблица тангенсов
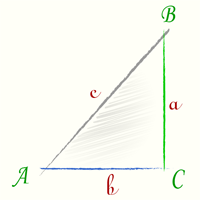
Тангенс, как отношение катетов в прямоугольном треугольнике, представляет собой функцию которая выглядит как дуга окружности внутри данного треугольника с центром в вершине угла и прилежащим катетом в качестве радиуса.

Значение тангенса показывает не только раскрытие угла α, но и насколько один катет больше другого. При тангенсе угла α, равном 1, катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
Подтемы
Смотрите также
|
Тангенс угла tg(A) — есть отношение [ tg(A) = frac{a}{b} ] |
Тангенс угла — tg(A), таблица
|
0° Тангенс угла 0 градусов |
$ tg(0°) = tg(0) = 0 $ |
0.000 |
|
30° Тангенс угла 30 градусов |
$ tg(30°) = tgBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{1}{sqrt{3}}normalsize $ |
0.577 |
|
45° Тангенс угла 45 градусов |
$ tg(45°) = tgBig(Largefrac{pi}{4}normalsizeBig) = 1 $ |
1.000 |
|
60° Тангенс угла 60 градусов |
$ tg(60°) = tgBig(Largefrac{pi}{3}normalsizeBig) = sqrt{3} $ |
1.732 |
|
90° Тангенс угла 90 градусов |
$ tg(90°) = tgBig(Largefrac{pi}{2}normalsizeBig) = infin $ |
∞ |
Вычислить, найти тангенс угла tg(A) и угол, в прямоугольном треугольнике
Вычислить, найти тангенс угла tg(A) по углу A в градусах
Вычислить, найти тангенс угла tg(A) по углу A в радианах
Тангенс угла — tg(A) |
стр. 224 |
|---|
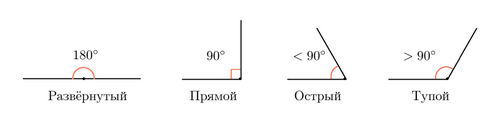
В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 900. Угол в котором меньше 90 градусов – называется острым. Угол в котором больше 90 градусов – называется тупым. В развернутом угле 180 градусов.
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла – называется катетом.
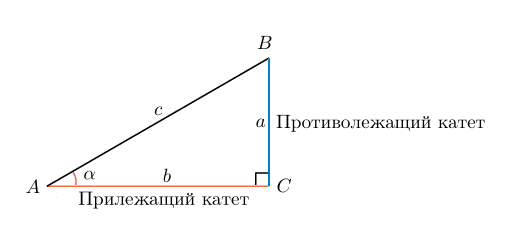
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
sinA = a/c
cosA = b/c
Формула тангенса
tg A = a/b
другими словами определение тангенса – это деление противоположного катета на прилежащий
Существует ещё одна равносильная формула тангенса
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Обозначения для основных углов:
тангенс 30 – 0,577
тангенс 45 – 1,000
тангенс 60 – 1,732
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
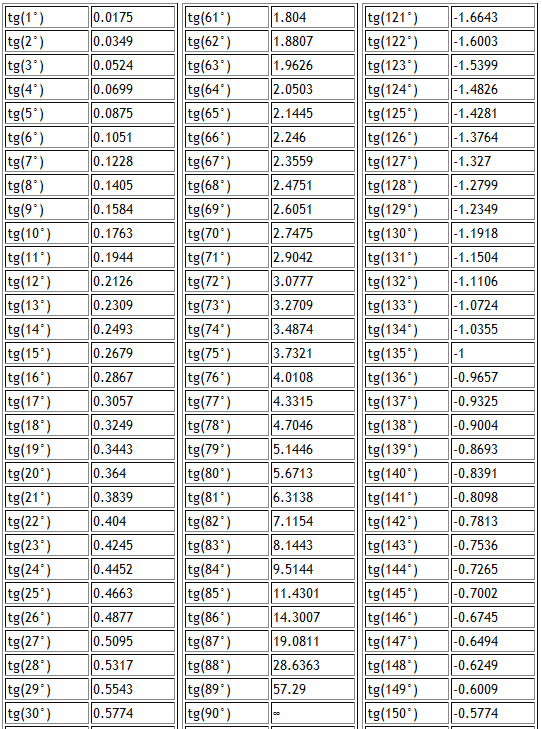
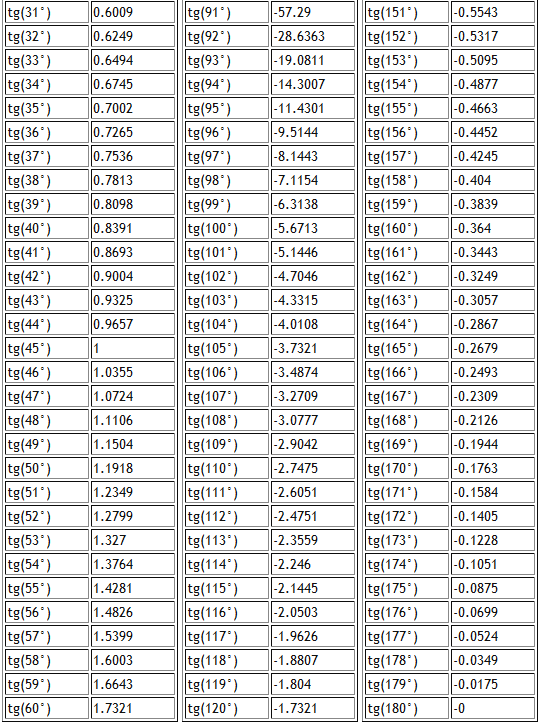
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.
В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.
Во втором случае гипотенуза превышает катет в ?2 раз.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Тангенс угла. Таблица тангенсов.
Тангенс угла через градусы, минуты и секунды
Тангенс угла через десятичную запись угла
Определение тангенса
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tg(α) = sin(α)/cos(α)
tg(α) = 1/ctg(α)
Таблица тангенсов в радианах
tg(0°) = 0tg(π/12) = tg(15°) = 0.2679491924tg(π/6) = tg(30°) = 0.5773502692tg(π/4) = tg(45°) = 1tg(π/3) = tg(60°) = 1.732050808tg(5π/12) = tg(75°) = 3.732050808tg(π/2) = tg(90°) = ∞tg(7π/12) = tg(105°) = -3.732050808tg(2π/3) = tg(120°) = -1.732050808tg(3π/4) = tg(135°) = -1tg(5π/6) = tg(150°) = -0.5773502692tg(11π/12) = tg(165°) = -0.2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924
Таблица Брадиса тангенсы
| tg(0) = 0 | tg(120) = -1.732050808 | tg(240) = 1.732050808 |
| tg(1) = 0.01745506493 | tg(121) = -1.664279482 | tg(241) = 1.804047755 |
| tg(2) = 0.03492076949 | tg(122) = -1.600334529 | tg(242) = 1.880726465 |
| tg(3) = 0.05240777928 | tg(123) = -1.539864964 | tg(243) = 1.962610506 |
| tg(4) = 0.06992681194 | tg(124) = -1.482560969 | tg(244) = 2.050303842 |
| tg(5) = 0.08748866353 | tg(125) = -1.428148007 | tg(245) = 2.144506921 |
| tg(6) = 0.1051042353 | tg(126) = -1.37638192 | tg(246) = 2.246036774 |
| tg(7) = 0.1227845609 | tg(127) = -1.327044822 | tg(247) = 2.355852366 |
| tg(8) = 0.1405408347 | tg(128) = -1.279941632 | tg(248) = 2.475086853 |
| tg(9) = 0.1583844403 | tg(129) = -1.234897157 | tg(249) = 2.605089065 |
| tg(10) = 0.1763269807 | tg(130) = -1.191753593 | tg(250) = 2.747477419 |
| tg(11) = 0.1943803091 | tg(131) = -1.150368407 | tg(251) = 2.904210878 |
| tg(12) = 0.2125565617 | tg(132) = -1.110612515 | tg(252) = 3.077683537 |
| tg(13) = 0.2308681911 | tg(133) = -1.07236871 | tg(253) = 3.270852618 |
| tg(14) = 0.2493280028 | tg(134) = -1.035530314 | tg(254) = 3.487414444 |
| tg(15) = 0.2679491924 | tg(135) = -1 | tg(255) = 3.732050808 |
| tg(16) = 0.2867453858 | tg(136) = -0.9656887748 | tg(256) = 4.010780934 |
| tg(17) = 0.3057306815 | tg(137) = -0.9325150861 | tg(257) = 4.331475874 |
| tg(18) = 0.3249196962 | tg(138) = -0.9004040443 | tg(258) = 4.704630109 |
| tg(19) = 0.3443276133 | tg(139) = -0.8692867378 | tg(259) = 5.144554016 |
| tg(20) = 0.3639702343 | tg(140) = -0.8390996312 | tg(260) = 5.67128182 |
| tg(21) = 0.383864035 | tg(141) = -0.8097840332 | tg(261) = 6.313751515 |
| tg(22) = 0.4040262258 | tg(142) = -0.7812856265 | tg(262) = 7.115369722 |
| tg(23) = 0.4244748162 | tg(143) = -0.7535540501 | tg(263) = 8.144346428 |
| tg(24) = 0.4452286853 | tg(144) = -0.726542528 | tg(264) = 9.514364454 |
| tg(25) = 0.4663076582 | tg(145) = -0.7002075382 | tg(265) = 11.4300523 |
| tg(26) = 0.4877325886 | tg(146) = -0.6745085168 | tg(266) = 14.30066626 |
| tg(27) = 0.5095254495 | tg(147) = -0.6494075932 | tg(267) = 19.08113669 |
| tg(28) = 0.5317094317 | tg(148) = -0.6248693519 | tg(268) = 28.63625328 |
| tg(29) = 0.5543090515 | tg(149) = -0.600860619 | tg(269) = 57.28996163 |
| tg(30) = 0.5773502692 | tg(150) = -0.5773502692 | tg(270) = ∞ |
| tg(31) = 0.600860619 | tg(151) = -0.5543090515 | tg(271) = -57.28996163 |
| tg(32) = 0.6248693519 | tg(152) = -0.5317094317 | tg(272) = -28.63625328 |
| tg(33) = 0.6494075932 | tg(153) = -0.5095254495 | tg(273) = -19.08113669 |
| tg(34) = 0.6745085168 | tg(154) = -0.4877325886 | tg(274) = -14.30066626 |
| tg(35) = 0.7002075382 | tg(155) = -0.4663076582 | tg(275) = -11.4300523 |
| tg(36) = 0.726542528 | tg(156) = -0.4452286853 | tg(276) = -9.514364454 |
| tg(37) = 0.7535540501 | tg(157) = -0.4244748162 | tg(277) = -8.144346428 |
| tg(38) = 0.7812856265 | tg(158) = -0.4040262258 | tg(278) = -7.115369722 |
| tg(39) = 0.8097840332 | tg(159) = -0.383864035 | tg(279) = -6.313751515 |
| tg(40) = 0.8390996312 | tg(160) = -0.3639702343 | tg(280) = -5.67128182 |
| tg(41) = 0.8692867378 | tg(161) = -0.3443276133 | tg(281) = -5.144554016 |
| tg(42) = 0.9004040443 | tg(162) = -0.3249196962 | tg(282) = -4.704630109 |
| tg(43) = 0.9325150861 | tg(163) = -0.3057306815 | tg(283) = -4.331475874 |
| tg(44) = 0.9656887748 | tg(164) = -0.2867453858 | tg(284) = -4.010780934 |
| tg(45) = 1 | tg(165) = -0.2679491924 | tg(285) = -3.732050808 |
| tg(46) = 1.035530314 | tg(166) = -0.2493280028 | tg(286) = -3.487414444 |
| tg(47) = 1.07236871 | tg(167) = -0.2308681911 | tg(287) = -3.270852618 |
| tg(48) = 1.110612515 | tg(168) = -0.2125565617 | tg(288) = -3.077683537 |
| tg(49) = 1.150368407 | tg(169) = -0.1943803091 | tg(289) = -2.904210878 |
| tg(50) = 1.191753593 | tg(170) = -0.1763269807 | tg(290) = -2.747477419 |
| tg(51) = 1.234897157 | tg(171) = -0.1583844403 | tg(291) = -2.605089065 |
| tg(52) = 1.279941632 | tg(172) = -0.1405408347 | tg(292) = -2.475086853 |
| tg(53) = 1.327044822 | tg(173) = -0.1227845609 | tg(293) = -2.355852366 |
| tg(54) = 1.37638192 | tg(174) = -0.1051042353 | tg(294) = -2.246036774 |
| tg(55) = 1.428148007 | tg(175) = -0.08748866353 | tg(295) = -2.144506921 |
| tg(56) = 1.482560969 | tg(176) = -0.06992681194 | tg(296) = -2.050303842 |
| tg(57) = 1.539864964 | tg(177) = -0.05240777928 | tg(297) = -1.962610506 |
| tg(58) = 1.600334529 | tg(178) = -0.03492076949 | tg(298) = -1.880726465 |
| tg(59) = 1.664279482 | tg(179) = -0.01745506493 | tg(299) = -1.804047755 |
| tg(60) = 1.732050808 | tg(180) = 0 | tg(300) = -1.732050808 |
| tg(61) = 1.804047755 | tg(181) = 0.01745506493 | tg(301) = -1.664279482 |
| tg(62) = 1.880726465 | tg(182) = 0.03492076949 | tg(302) = -1.600334529 |
| tg(63) = 1.962610506 | tg(183) = 0.05240777928 | tg(303) = -1.539864964 |
| tg(64) = 2.050303842 | tg(184) = 0.06992681194 | tg(304) = -1.482560969 |
| tg(65) = 2.144506921 | tg(185) = 0.08748866353 | tg(305) = -1.428148007 |
| tg(66) = 2.246036774 | tg(186) = 0.1051042353 | tg(306) = -1.37638192 |
| tg(67) = 2.355852366 | tg(187) = 0.1227845609 | tg(307) = -1.327044822 |
| tg(68) = 2.475086853 | tg(188) = 0.1405408347 | tg(308) = -1.279941632 |
| tg(69) = 2.605089065 | tg(189) = 0.1583844403 | tg(309) = -1.234897157 |
| tg(70) = 2.747477419 | tg(190) = 0.1763269807 | tg(310) = -1.191753593 |
| tg(71) = 2.904210878 | tg(191) = 0.1943803091 | tg(311) = -1.150368407 |
| tg(72) = 3.077683537 | tg(192) = 0.2125565617 | tg(312) = -1.110612515 |
| tg(73) = 3.270852618 | tg(193) = 0.2308681911 | tg(313) = -1.07236871 |
| tg(74) = 3.487414444 | tg(194) = 0.2493280028 | tg(314) = -1.035530314 |
| tg(75) = 3.732050808 | tg(195) = 0.2679491924 | tg(315) = -1 |
| tg(76) = 4.010780934 | tg(196) = 0.2867453858 | tg(316) = -0.9656887748 |
| tg(77) = 4.331475874 | tg(197) = 0.3057306815 | tg(317) = -0.9325150861 |
| tg(78) = 4.704630109 | tg(198) = 0.3249196962 | tg(318) = -0.9004040443 |
| tg(79) = 5.144554016 | tg(199) = 0.3443276133 | tg(319) = -0.8692867378 |
| tg(80) = 5.67128182 | tg(200) = 0.3639702343 | tg(320) = -0.8390996312 |
| tg(81) = 6.313751515 | tg(201) = 0.383864035 | tg(321) = -0.8097840332 |
| tg(82) = 7.115369722 | tg(202) = 0.4040262258 | tg(322) = -0.7812856265 |
| tg(83) = 8.144346428 | tg(203) = 0.4244748162 | tg(323) = -0.7535540501 |
| tg(84) = 9.514364454 | tg(204) = 0.4452286853 | tg(324) = -0.726542528 |
| tg(85) = 11.4300523 | tg(205) = 0.4663076582 | tg(325) = -0.7002075382 |
| tg(86) = 14.30066626 | tg(206) = 0.4877325886 | tg(326) = -0.6745085168 |
| tg(87) = 19.08113669 | tg(207) = 0.5095254495 | tg(327) = -0.6494075932 |
| tg(88) = 28.63625328 | tg(208) = 0.5317094317 | tg(328) = -0.6248693519 |
| tg(89) = 57.28996163 | tg(209) = 0.5543090515 | tg(329) = -0.600860619 |
| tg(90) = ∞ | tg(210) = 0.5773502692 | tg(330) = -0.5773502692 |
| tg(91) = -57.28996163 | tg(211) = 0.600860619 | tg(331) = -0.5543090515 |
| tg(92) = -28.63625328 | tg(212) = 0.6248693519 | tg(332) = -0.5317094317 |
| tg(93) = -19.08113669 | tg(213) = 0.6494075932 | tg(333) = -0.5095254495 |
| tg(94) = -14.30066626 | tg(214) = 0.6745085168 | tg(334) = -0.4877325886 |
| tg(95) = -11.4300523 | tg(215) = 0.7002075382 | tg(335) = -0.4663076582 |
| tg(96) = -9.514364454 | tg(216) = 0.726542528 | tg(336) = -0.4452286853 |
| tg(97) = -8.144346428 | tg(217) = 0.7535540501 | tg(337) = -0.4244748162 |
| tg(98) = -7.115369722 | tg(218) = 0.7812856265 | tg(338) = -0.4040262258 |
| tg(99) = -6.313751515 | tg(219) = 0.8097840332 | tg(339) = -0.383864035 |
| tg(100) = -5.67128182 | tg(220) = 0.8390996312 | tg(340) = -0.3639702343 |
| tg(101) = -5.144554016 | tg(221) = 0.8692867378 | tg(341) = -0.3443276133 |
| tg(102) = -4.704630109 | tg(222) = 0.9004040443 | tg(342) = -0.3249196962 |
| tg(103) = -4.331475874 | tg(223) = 0.9325150861 | tg(343) = -0.3057306815 |
| tg(104) = -4.010780934 | tg(224) = 0.9656887748 | tg(344) = -0.2867453858 |
| tg(105) = -3.732050808 | tg(225) = 1 | tg(345) = -0.2679491924 |
| tg(106) = -3.487414444 | tg(226) = 1.035530314 | tg(346) = -0.2493280028 |
| tg(107) = -3.270852618 | tg(227) = 1.07236871 | tg(347) = -0.2308681911 |
| tg(108) = -3.077683537 | tg(228) = 1.110612515 | tg(348) = -0.2125565617 |
| tg(109) = -2.904210878 | tg(229) = 1.150368407 | tg(349) = -0.1943803091 |
| tg(110) = -2.747477419 | tg(230) = 1.191753593 | tg(350) = -0.1763269807 |
| tg(111) = -2.605089065 | tg(231) = 1.234897157 | tg(351) = -0.1583844403 |
| tg(112) = -2.475086853 | tg(232) = 1.279941632 | tg(352) = -0.1405408347 |
| tg(113) = -2.355852366 | tg(233) = 1.327044822 | tg(353) = -0.1227845609 |
| tg(114) = -2.246036774 | tg(234) = 1.37638192 | tg(354) = -0.1051042353 |
| tg(115) = -2.144506921 | tg(235) = 1.428148007 | tg(355) = -0.08748866353 |
| tg(116) = -2.050303842 | tg(236) = 1.482560969 | tg(356) = -0.06992681194 |
| tg(117) = -1.962610506 | tg(237) = 1.539864964 | tg(357) = -0.05240777928 |
| tg(118) = -1.880726465 | tg(238) = 1.600334529 | tg(358) = -0.03492076949 |
| tg(119) = -1.804047755 | tg(239) = 1.664279482 | tg(359) = -0.01745506493 |
Похожие калькуляторы
Что такое тангенс угла и как его найти
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение…
Итак, есть два определения:
-
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
-
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
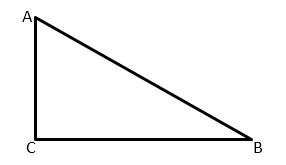
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
![]()
Так как тангенс – это отношение катетов, то
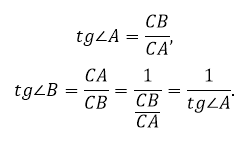
Получается, что
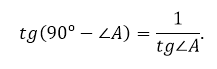
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
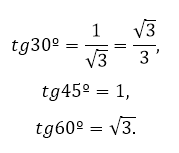
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
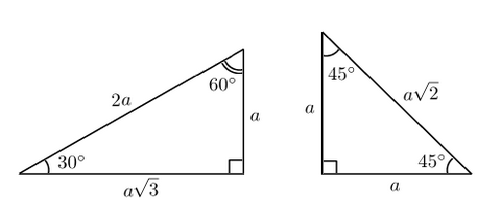
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
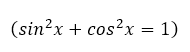
Из формулы тангенсов, записывающей кратко второе определение
![]()
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:
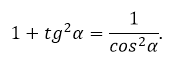
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом: