Тема как найти среднюю скорость - Сайт, где вы сможете решить свои вопросы

Средняя скорость считается так: весь путь поделить на всё время движения. Формула одна и очень простая, но почему-то школьники часто путаются в задачах на среднюю скорость. Разберу три характерные задачи и основные ошибки. Возможно, статья будет полезна учителям и репетиторам, а также школьникам.

1. Половина пути

Первую половину пути поезд ехал со скоростью 60 км/ч, а вторую – 90 км/ч. С какой средней скоростью ехал поезд на всём пути?

Первым делом школьник захочет сложить эти две скорости и поделить пополам. Логично? Да. Но, к сожалению, неправильно.

Объясняю, почему. Поскольку первую половину пути поезд ехал с меньшей скоростью, то времени было затрачено больше, чем на вторую. А значит, вклад отдельных скоростей неравнозначен, и нельзя так просто делить пополам.

Тут школьник может впасть в панику. Что делать? Умножать? Делить? Непонятно. Воспользоваться напрямую формулой “расстояние поделить на время” не получится – ни расстояние, ни время нам неизвестно.

Для школьников, только начинающих изучать основы физики, бывает трудно оперировать с неизвестными величинами. Нам не дано ничего, кроме скоростей, как же быть? В качестве маленькой ступеньки к освоению неизвестности могу предложить следующий ход – сначала додумать неизвестные данные. Возьмём и сами решим, пусть поезд пройдет 180 километров, цифру возьмем так, чтобы легко делилась.

Тогда половина пути будет 90 километров. Поезд пройдет её за 1,5 часа. Вторую половину пути – за 1 час. Это легко посчитает любой школьник. Значит, общее время в пути будет 2,5 часа. Делим общее расстояние 180 километров на 2,5 часа, и получаем 72 км/ч.

Это просто и понятно, но учитель такую задачу не примет. Откуда мы взяли 180 километров, когда это неизвестно? Тем не менее, дав себе эти неизвестные данные, мы продумали алгоритм и довели задачу до ответа. Осталось формализовать это решение, так чтобы не использовать то, что не дано. Обозначим наши 180 километров за S, и опишем всё, что мы делали раньше, только вместо цифр используем буквы.

Решение задачи про среднюю скорость поезда. Паровозик из Ромашково тут для красоты.

Получается, что зная ход решения “в цифрах”, мы переводим его в буквенные обозначения. И тут главное не остановиться на полдороги, не смущаться, что нам неизвестно расстояние. Ведь оно в конце сократилось, и средняя скорость оказалась независящей от расстояния (что вполне логично). И от школьника здесь требуются уже алгебраические умения – складывать дроби, переворачивать их.

Если подобная задача встретилась в тесте, где требуется только ответ, можно вообще не заморачиваться – так как средняя скорость в данной задаче не зависит от расстояния, можно посчитать при любом удобном расстоянии. По крайней мере, это лучше, чем сидеть и ломать голову, не зная, как подступиться к решению. Если же требуется оформление – тут числовое решение может помочь как переходный этап, чтобы понять, что именно делать с формулами, как их крутить-вертеть.

Школьникам часто бывает трудно переходить на новый уровень абстракции – от чисел к переменным, которые могут принимать разные числовые значения. В алгебре это тренируют, но там одна переменная икс, и иногда игреки встречаются. А в физике этих переменных пруд пруди, в каждой задаче они разные, и если ученик не освоил этот уровень, то физика кажется ему супер-трудной. Кроме того, в школе переход от чисел к переменным часто упускают, в программе отдельных навыков работы с формулами нет.

2. Средняя скорость по графику пути

Пусть нам дан график зависимости координаты от времени. Требуется определить среднюю скорость.

График координаты от времени для примера

По графику видно, что движение состоит из четырех этапов:

Тело стартует в нуле и через 2 секунды оказывается на координате 2 м.
Тело останавливается, и в течение 4 секунд покоится в точке с координатой 2 м.
Тело начинает движение, и через 2 секунды оказывается в точке 6 м.
Тело движется в обратном направлении, и через 2 секунды оказывается в точке 5 м.

Проговорить, понять все эти этапы – важная часть решения. А дальше многие школьники начинают вычислять скорости движения на каждом этапе: На первом – 1 м/с, на втором – 0, на третьем – 2 м/с, на четвертом – 0,5 м/с. Вот это действие как раз лишнее. Для того, чтобы вычислить среднюю скорость, вовсе не обязательно знать скорости на каждом этапе!

Вспомним определение средней скорости – это весь путь, поделить на всё время. Поэтому просто по графику считаем весь путь – 6 метров “туда” и 1 метр “обратно”, в сумме 7 метров. Общее время движения – 10 секунд. Делим 7 метров на 10 секунд, получаем 0,7 м/с.

3. Средняя скорость по графику скорости

Бывает так, что нам дан график зависимости скорости от времени, и требуется определить среднюю скорость. Вот, к примеру, такой график.

Для примера, график зависимости скорости от времени.

Читаем график. Движение состоит из трёх этапов

С начала движения до момента времени 2 с тело движется с постоянной скоростью 2 м/с
От 2 до 6 с тело движется со скоростью 6 м/с
В последние 4 секунды от 6 до 10 с тело замедляется, снижая свою скорость до нуля.

Попытки что-то сделать со значениями скорости самими по себе здесь обречены на провал. Опять надо найти весь путь и всё время движения. Путь по графику скорости определяется как площадь под графиком, причем если график идет ниже нуля, то соответствующие участки складываются.

Считаем площадь фигуры – два прямоугольника на первых двух этапах и треугольник на третьем. Первый этап – 4 м, второй этап – 24 м, третий этап – 12 м. Значит, весь путь будет 40 метров. Всё время 10 секунд, значит, средняя скорость 4 м/с.

Общие рекомендации для решения задач на среднюю скорость

1. Средняя скорость – это всегда весь путь делить на всё время. Данные об отдельных скоростях сами по себе не дадут полной информации о средней скорости. Используем только эту формулу.

2. Следует проанализировать конкретную ситуацию и понять, как можно применить формулу. Если кажется, что не хватает данных – не смущаться.

3. Данные по скоростям на отдельных этапах могут быть полезны для проверки готового ответа: средняя скорость должна лежать между минимальной и максимальной.

Спасибо, что прочитали до конца! Желаю школьникам хорошей учёбы, учителям – понятливых и любопытных учеников, родителям – чтобы дети радовали. Буду рада лайкам и новым подписчикам!

Источник

Средняя скорость

4.6

Средняя оценка: 4.6

Всего получено оценок: 166.

Обновлено 13 Июля, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 166.

Обновлено 13 Июля, 2021

Важнейшей характеристикой тела в кинематике является скорость, с которой оно движется. Движение с нулевой скоростью фактически вообще не является движением. Однако скорость можно измерять различными методами и получать различные значения. Например, можно находить среднюю скорость. Рассмотрим эту тему подробнее: дадим определение средней скорости, приведем формулу средней скорости.

Движение и его скорость

Движение — это изменение координаты материальной точки со временем. Для вычисления быстроты изменения координаты используется такая физическая величина, как скорость (для обозначения используется символ $v$):

$$v={Delta x over Delta t}$$

Если движение происходит равномерно, то это отношение всегда будет одинаковым, независимо от выбора момента времени.

Например, если автомобиль движется со скоростью 36 км/ч, то за время $Delta t = 5c$ он пройдет расстояние $Delta x = 50м$, а за время $Delta t = 60c$ он пройдет расстояние $Delta x = 600м$.

Отношение пройденного расстояния ко времени перемещения в обоих случаях будет одинаковым и равным $v=10$м/с. Это и есть скорость движения автомобиля в данном примере.

Рис. 1. Скорость движения.

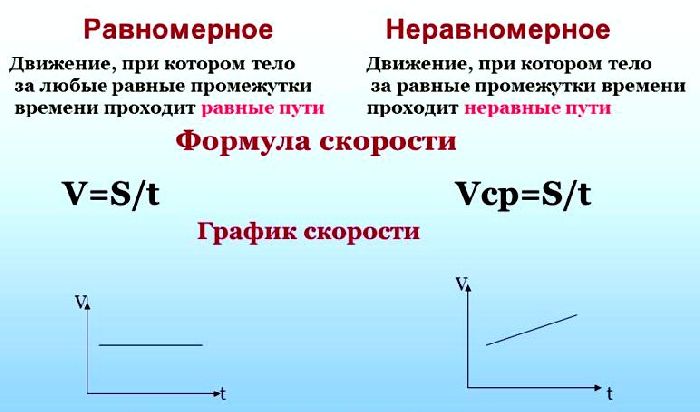
Равномерное и неравномерное движение

Заметим, что автомобиль в приведенном примере на рассматриваемом промежутке времени $Delta t$ двигается равномерно. Но такое движение встречается довольно редко.

Тот же автомобиль когда-то стоял на месте, затем начал разгон и лишь потом двигался равномерно. А если рассмотреть ситуацию дальше — то рано или поздно автомобиль начнет замедление и остановится.

Получается, что скорость движения в рассматриваемом промежутке времени может изменяться. Движение с изменяемой скоростью называется неравномерным.

Рис. 2. Равномерное и неравномерное движение.

Средняя скорость

Как можно сравнивать скорости неравномерных движений?

Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.

Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.

В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени. Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта. Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.

Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается.

Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.

$$v_{ср}={Delta x_{общ} over Delta t_{общ}}$$

Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.

Рис. 3. Средняя скорость.

Что мы узнали?

Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 166.

А какая ваша оценка?

Источник

Средняя скорость. Решение задач по физике

Подробности: Обновлено 02.09.2018 15:56; Просмотров: 2375

Задачи по физике – это просто!

Среднюю скорость движения иначе называют путевой скоростью.

где

Sобщ – общий путь, т.е. сумма всех отрезков пути

t общ – общее время, т.е. время, за которое был пройден весь путь

При решении задач очень помогает простенький чертеж, на котором надо показать все отрезки пути.
Около каждого отрезка для наглядности укажите буквенные обозначения скорости, времени, пути (с нужным индексом) и формулы для их расчета (если это необходимо).

Переходим к решению задач.
От простых к сложным!

Элементарные задачи из курса школьной физики

Задача 1

Автомобиль проехал 100 метров за 25 секунд, а следующие 300 метров за 1 минуту.
Определить среднюю скорость движения автомобиля.

Задача 2

Автомобиль ехал 2 минуты со скоростью 10 м/с, а затем проехал еще 500 метров за 30 секунд.
Определить среднюю скорость движения.

Задача
3

Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 20 м/c.
Определить среднюю скорость автомобиля.

Задача 4

Автомобиль проехал первую половину пути со скоростью 10 м/с, а вторую половину пути со скоростью 20 м/с. Определить среднюю скорость автомобиля на всем пути.

Пусть S – общий пройденный путь.

Задача 5

Автомобиль одну треть времени движения ехал со скоростью 10 м/с, а остальное время со скоростью 20 м/с. Определить среднюю скорость за все время движения.

Пусть t – общее время движения.

Источник

Запомните!

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму
на их количество.

Пример:

Найти среднее арифметическое 2, 3 и 4.

Обозначим среднее арифметическое буквой «m». По определению выше найдем сумму всех чисел.

2 + 3 + 4 = 9

Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.

В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?

Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.

Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой
цене вам продавать мячи.

Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены
в магазинах и составим таблицу.

Магазин	Цена футбольного мяча
«Спорт-товары»	290 руб.
«Adidas»	360 руб.
«Все для футбола»	310 руб.

Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?

Если выбрать самую низкую (290 руб.), то мы будем продавать
товар себе в убыток. Если выбрать самую высокую (360 руб.), то покупатели не будут приобретать футбольные мячи у нас.

Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.

Вычислим среднее арифметическое цен на футбольные мячи:

Средняя цена = =
= 320 руб.

Таким образом, мы получили среднюю цену (320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не
слишком дорого.

Средняя скорость движения

Со средним арифметическим тесно связано понятие средней скорости движения.

Наблюдая за движением транспорта в городе, можно заметить, что машины, то
разгоняются и едут с большой скоростью, то замедляются и едут с
маленькой скоростью.

Таких участков на пути следования автотранспорта бывает много. Поэтому
для удобства расчётов, используют понятие средней скорости движения.

Запомните!

Средняя скорость движения — это весь пройденный путь разделить на всё время движения.

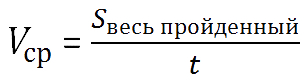
Рассмотрим задачу на среднюю скорость.

Разбор примера

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем
1,5 ч по
грунтовой дороге со скоростью 45 км/ч, наконец
0,3 ч по просёлочной дороге со скоростью 30 км/ч.
Найдите среднюю скорость движения автомобиля на всём пути.

Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем,
и всё время, которое автомобиль двигался.

S₁ = V₁t₁

S₁ = 90 · 3,2 = 288 (км)

— шоссе.

S₂ = V₂t₂

S₂ = 45 · 1,5 = 67,5 (км)

— грунтовая дорога.

S₃ = V₃t₃

S₃ = 30 · 0,3 = 9 (км)

— просёлочная дорога.

S = S₁ + S₂ + S₃

S = 288 + 67,5 + 9 = 364,5 (км)

— весь путь, пройденный автомобилем.

t = t₁ + t₂ + t₃

t = 3,2 + 1,5 + 0,3 = 5 (ч)

— всё время.

V_ср = S : t

V_ср = 364,5 : 5 = 72,9

(км/ч) — средняя скорость движения автомобиля.

Ответ: V_ср = 72,9 (км/ч) — средняя скорость движения автомобиля.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

10 апреля 2015 в 18:52

Дарья Некрасова
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Дарья Некрасова
Профиль
Благодарили: 0

Сообщений: 3

Автомобиль проехал 180 км за 3 ч с одинаковой скоростью. Из-за гололёда на обратном пути он уменьшил скорость на 15 км/ч. Сколько времени затратил автомобиль на обратный путь.

0
Спасибо thanks
Ответить

10 апреля 2015 в 18:55
Ответ для Дарья Некрасова

Дарья Некрасова
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Дарья Некрасова
Профиль
Благодарили: 0

Сообщений: 3

180: 3=60
60 ?15=45
180 :45=4

0
Спасибо thanks
Ответить

14 апреля 2015 в 17:11
Ответ для Дарья Некрасова

Asel Talantbekovna
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Asel Talantbekovna
Профиль
Благодарили: 0

Сообщений: 8

сама себе отвечает?

0
Спасибо thanks
Ответить

Источник

Загрузить PDF

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: ${text{Скорость}}={frac {{text{Пройденный путь}}}{{text{Время}}}}$ . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
- длина пути, пройденного телом;
- время, за которое тело прошло этот путь.
- Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.
2

Запишите формулу для вычисления средней скорости. Формула: $v={frac {s}{t}}$ , где — средняя скорость, — пройденный путь, — время, за которое пройден путь.^[1]
3
В формулу подставьте пройденный путь. Значение пути подставьте вместо .
- В нашем примере автомобиль проехал 150 км. Формула запишется так: $v={frac {150}{t}}$ .
4
В формулу подставьте время. Значение времени подставьте вместо .
- В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: $v={frac {150}{3}}$ .
5

Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
- несколько значений пройденных участков пути;
- несколько значений времени, за которые был пройден каждый участок пути.^[2]
- Например: автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2

Запишите формулу для вычисления средней скорости. Формула: $v={frac {s}{t}}$ , где — средняя скорость, — общий пройденный путь, — общее время, за которое пройден путь.^[3]
3

Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо ).
4

Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо ).
5

Разделите общий путь на общее время. Вы найдете среднюю скорость.

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
- несколько значений скоростей, с которыми двигалось тело;
- несколько значений времени, в течение которого тело двигалось с соответствующей скоростью.^[4]
- Например: автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2

Запишите формулу для вычисления средней скорости. Формула: $v={frac {s}{t}}$ , где — средняя скорость, — общий пройденный путь, — общее время, за которое пройден путь.^[5]
3

Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо ).
4

Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо ).
5

Разделите общий путь на общее время. Вы найдете среднюю скорость.

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:
- два или несколько значений скоростей, с которыми двигалось тело;
- тело двигалось с определенными скоростями в течение равных промежутков времени.
- Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2
3
4

Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:
- два или несколько значений скоростей, с которыми двигалось тело;
- тело двигалось с определенными скоростями и прошло равные участки пути.
- Например: автомобиль проехал 150 км со скоростью 40 км/ч, а затем вернулся обратно (то есть проехал те же 160 км) со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2
Запишите формулу для вычисления средней скорости, если даны две скорости и одинаковые значения участков пути. Формула: $v={frac {2ab}{a+b}}$ , где — средняя скорость, — скорость тела, с которым оно двигалось на первом участке пути, — скорость тела, с которым оно двигалось на втором (таком же, как первый) участке пути.
^[7]
- Зачастую в условиях таких задач дано, что тело прошло определенный путь и вернулось обратно.
- В таких задачах значения участков пути не важны — главное, чтобы они были равны.
- Если даны три скорости и равные участки пути, перепишите формулу так: $v={frac {3abc}{ab+bc+ca}}$ .^[8]
3
4

Произведение двух скоростей умножьте на 2. Полученный результат запишите в числителе дроби.
5

Сложите две скорости. Полученный результат запишите в знаменателе дроби.
6

Сократите дробь. Вы найдете среднюю скорость на всем протяжении пути.

Реклама