Теорема пифагора 8 класс как найти катет - Сайт, где вы сможете решить свои вопросы

Теорема Пифагора

Названо в честь	Пифагор
Описывающая закон или теорему формула	$c^{2}=a^{2}+b^{2}$
Обозначение в формуле	, и
Элемент или утверждение описывает	прямоугольный треугольник
Описывается по ссылке	geogebra.org/m/ZF… (англ.)
Медиафайлы на Викискладе

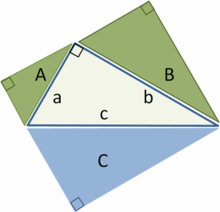
Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость^[⇨]

Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору.
Утверждение появляется как Предложение 47 в «Началах» Евклида^[⇨].

Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение^[⇨]: треугольник, у которого сумма квадратов длин двух сторон равна квадрату длины третьей стороны, является прямоугольным.

Существует ряд обобщений данной теоремы^[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется^[⇨].

История[править | править код]

По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок»^[1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы^[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы^[3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.

Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки^[⇨]^[4], но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако когда Плутарх и Цицерон пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненно^[5]^[6]. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков^[7].

Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора^[8].

Формулировки[править | править код]

Сумма площадей квадратов, опирающихся на катеты и , равна площади квадрата, построенного на гипотенузе

Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны и , а длина гипотенузы — , выполнено соотношение $a^{2}+b^{2}=c^{2}$ .

Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
В таком виде теорема сформулирована в «Началах» Евклида.

Для того чтобы треугольник являлся прямоугольным, необходимо и достаточно, чтобы сумма квадратов двух сторон треугольника была равна квадрату третьей стороны^[9].

Пифагор, 572–500 г. до н. э.

Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением $a^{2}+b^{2}=c^{2}$ . Как следствие, для всякой тройки положительных чисел , и , такой, что $a^{2}+b^{2}=c^{2}$ , существует прямоугольный треугольник с катетами и и гипотенузой . Предложение, обратное теореме Пифагора, сформулированное в условной форме: «Если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то угол, лежащий против этой стороны, является прямым». Это же предложение в категоричной форме: «Угол треугольника, лежащий против стороны, квадрат которой равен сумме квадратов двух других сторон, прямой». Именно данное корректное предложение, обратное теореме Пифагора, является также теоремой^[10].

Доказательства[править | править код]

В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора^[11], что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия^[⇨]), метод площадей^[⇨], существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники[править | править код]

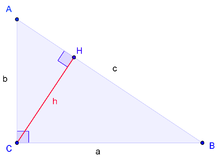
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры^[12].
В нём для треугольника с прямым углом при вершине со сторонами a,b,c , противолежащими вершинам A,B,C соответственно, проводится высота , при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: и , из чего непосредственно следуют соотношения

${displaystyle {frac {a}{c}}={frac {|HB|}{a}},quad {frac {b}{c}}={frac {|AH|}{b}}.}$

При перемножении крайних членов пропорций выводятся равенства

${displaystyle a^{2}=ccdot |HB|,quad b^{2}=ccdot |AH|,}$

покомпонентное сложение которых даёт требуемый результат:

${displaystyle a^{2}+b^{2}=ccdot {big (}|HB|+|AH|{big )}=c^{2}quad Longleftrightarrow quad a^{2}+b^{2}=c^{2}.}$

Доказательства методом площадей[править | править код]

Большое число доказательств задействуют понятие площади.
Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость[править | править код]

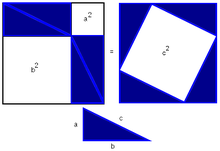
Схема доказательства через равнодополняемость

Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами a,b и гипотенузой , расположенные таким образом, чтобы образовывать квадрат со стороной a+b и внутренний четырёхугольник со сторонами длиной . Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна ${displaystyle (a+b)^{2}}$ , он состоит из внутреннего квадрата площадью $c^{2}$ и четырёх прямоугольных треугольников, каждый площадью ${frac {ab}{2}}$ , в результате из соотношения ${displaystyle (a+b)^{2}=4cdot {frac {ab}{2}}+c^{2}}$ при алгебраическом преобразовании следует утверждение теоремы.

Доказательство Евклида[править | править код]

Чертёж к доказательству Евклида. Основное направление доказательства — установление конгруэнтности , площадь которых составляет половину площади прямоугольников и соответственно

Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами^[13].

Конструкция, используемая для доказательства следующая: для прямоугольного треугольника с прямым углом , квадратов над катетами и и квадрата над гипотенузой строится высота и продолжающий её луч , разбивающий квадрат над гипотенузой на два прямоугольника и . Доказательство нацелено на установление равенства площадей прямоугольника с квадратом над катетом ; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.

Равенство площадей прямоугольника и устанавливается через конгруэнтность треугольников и , площадь каждого из которых равна половине площади прямоугольников и соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямого угла и угла при ).

Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников и , равна сумме площадей квадратов над катетами.

Доказательство Леонардо да Винчи[править | править код]

К методу площадей относится также доказательство, приписываемое Леонардо да Винчи. По данным немецкого математика Франца Леммермейера (нем. Franz Lemmermeyer), в действительности это доказательство было придумано Иоганном Тобиасом Майером^[14]. Пусть дан прямоугольный треугольник с прямым углом и квадраты , и ABHJ (см. рисунок). В этом доказательстве на стороне последнего во внешнюю сторону строится треугольник, конгруэнтный , притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть и ). Прямая разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники и равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников CAJI и DABG , площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.

Через площади подобных треугольников[править | править код]

Следующее доказательство основано на том, что площади подобных треугольников относятся как квадраты соответственных сторон^[15].

Пусть ABC есть прямоугольный треугольник, — перпендикуляр, опущенный на гипотенузу из вершины прямого угла.
Треугольники ABC , подобны, так как имеют по прямому углу и ещё общий угол .
Значит

${displaystyle {frac {{text{площадь}}~DBA}{{text{площадь}}~ABC}}={frac {AB^{2}}{BC^{2}}}.}$

Точно также получаем, что

${displaystyle {frac {{text{площадь}}~DAC}{{text{площадь}}~ABC}}={frac {AC^{2}}{BC^{2}}}.}$

Поскольку треугольники и вместе составляют , сумма площадей
и равна площади .
Отсюда

${displaystyle {frac {AB^{2}+AC^{2}}{BC^{2}}}=1}$

или
${displaystyle AB^{2}+AC^{2}=BC^{2}.}$

Доказательство методом бесконечно малых[править | править код]

Доказательство методом бесконечно малых

Существует несколько доказательств, прибегающих к технике дифференциальных уравнений. В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов и и гипотенузы . Например, приращение катета при постоянном катете приводит к приращению гипотенузы , так что

${displaystyle {frac {da}{dc}}={frac {c}{a}}.}$

Методом разделения переменных из них выводится дифференциальное уравнение ,
интегрирование которого даёт соотношение ${displaystyle c^{2}=a^{2}+mathrm {const} }$ . Применение начальных условий определяет константу как $b^{2}$ , что в результате даёт утверждение теоремы.

Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Вариации и обобщения[править | править код]

Подобные геометрические фигуры на трёх сторонах[править | править код]

Обобщение для подобных треугольников, сумма площадей зелёных фигур равна площади синей

Теорема Пифагора с использованием подобных прямоугольных треугольников

Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах», перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур^[16]: сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями , и , построенных на катетах с длинами и и гипотенузе соответственно, имеет место соотношение:

${displaystyle {frac {A}{a^{2}}}={frac {B}{b^{2}}}={frac {C}{c^{2}}},Rightarrow ,A+B={frac {a^{2}}{c^{2}}}C+{frac {b^{2}}{c^{2}}}C}$

Так как по теореме Пифагора $a^{2}+b^{2}=c^{2}$ , то выполнено .

Кроме того, если возможно доказать без привлечения теоремы Пифагора, что для площадей трёх подобных геометрических фигур на сторонах прямоугольного треугольника выполнено соотношение , то с использованием обратного хода доказательства обобщения Евклида можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить конгруэнтный начальному прямоугольный треугольник площадью , а на катетах — два подобных ему прямоугольных треугольника с площадями и , то оказывается, что треугольники на катетах образуются в результате деления начального треугольника его высотой, то есть сумма двух меньших площадей треугольников равна площади третьего, таким образом и, применяя соотношение для подобных фигур, выводится теорема Пифагора.

Теорема косинусов[править | править код]

Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике^[17]:

${displaystyle a^{2}+b^{2}-2abcos {theta }=c^{2}}$

где theta — угол между сторонами и . Если угол равен 90°, то , и формула упрощается до обычной теоремы Пифагора.

Произвольный треугольник[править | править код]

Обобщение, установленное Сабитом ибн Куррой. Нижний рисунок демонстрирует подобие треугольника треугольнику

Существует обобщение теоремы Пифагора на произвольный треугольник, оперирующее исключительно соотношением длин сторон. Считается, что оно впервые было установлено сабийским астрономом Сабитом ибн Куррой^[18]. В нём для произвольного треугольника со сторонами a,b,c в него вписывается равнобедренный треугольник с основанием на стороне , вершиной, совпадающей с вершиной исходного треугольника, противолежащей стороне и углами при основании, равными углу theta , противолежащему стороне . В результате образуются два треугольника, подобных исходному: первый — со сторонами , дальней от неё боковой стороной вписанного равнобедренного треугольника, и — части стороны ; второй — симметрично к нему от стороны со стороной — соответствующей частью стороны . В результате оказывается выполнено соотношение^[19]^[20]

${displaystyle a^{2}+b^{2}=c(r+s),}$

вырождающееся в теорему Пифагора при . Соотношение является следствием подобия образованных треугольников:

${displaystyle {frac {c}{a}}={frac {a}{r}},quad {frac {c}{b}}={frac {b}{s}}quad Rightarrow quad cr+cs=a^{2}+b^{2}.}$

Теорема Паппа о площадях[править | править код]

Теорема Паппа о площадях, позволяющая для произвольного треугольника и произвольных параллелограммов на двух его сторонах построить параллелограмм на третьей стороне таким образом, чтобы его площадь была равна сумме площадей двух заданных параллелограммов, также может быть рассмотрена как обобщение теоремы Пифагора^[21]: в случае, когда исходный треугольник — прямоугольный, а на катетах в качестве параллелограммов заданы квадраты, квадрат, построенный на гипотенузе оказывается удовлетворяющим условиям теоремы Паппа о площадях.

Многомерные обобщения[править | править код]

Обобщением теоремы Пифагора для трёхмерного евклидова пространства является теорема де Гуа: если в одной вершине тетраэдра сходятся три прямых угла, то квадрат площади грани, лежащей напротив этой вершины, равен сумме квадратов площадей других трёх граней. Этот вывод может быть обобщён и как «n-мерная теорема Пифагора» для евклидовых пространств высших размерностей^[22] — для граней ортогонального -мерного симплекса с площадями ${displaystyle S_{1},dots ,S_{n}}$ ортогональных граней и противолежащей им грани площадью $S_{0}$ выполнено соотношение:

${displaystyle S_{0}^{2}=sum _{i=1}^{n}S_{i}^{2}}$

Ещё одно многомерное обобщение возникает из задачи нахождения квадрата длины диагонали прямоугольного параллелепипеда: для её вычисления необходимо дважды применить теорему Пифагора, в результате она составит сумму квадратов длин трёх смежных сторон параллелепипеда. В общем случае, длина диагонали -мерного прямоугольного параллелепипеда со смежными сторонами с длинами $a_{1},dots ,a_{n}$ составляет:

${displaystyle d^{2}=sum _{i=1}^{n}a_{i}^{2}}$

как и в трёхмерном случае, результат является следствием последовательного применения теоремы Пифагора к прямоугольным треугольникам в перпендикулярных плоскостях.

Обобщением теоремы Пифагора для бесконечномерного пространства является равенство Парсеваля^[23].

Неевклидова геометрия[править | править код]

Теорема Пифагора выводится из аксиом евклидовой геометрии и недействительна для неевклидовой геометрии^[24] — выполнение теоремы Пифагора равносильно постулату Евклида о параллельности^[25]^[26].

В неевклидовой геометрии соотношение между сторонами прямоугольного треугольника обязательно будет в форме, отличной от теоремы Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника, которые ограничивают собой октант единичной сферы, имеют длину pi/2 , что противоречит теореме Пифагора.

При этом теорема Пифагора справедлива в гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему^[27].

Сферическая геометрия[править | править код]

Для любого прямоугольного треугольника на сфере радиусом (например, если угол gamma в треугольнике прямой) со сторонами a,b,c соотношение между сторонами имеет вид^[28]

${displaystyle cos {frac {c}{R}}=cos {frac {a}{R}}cdot cos {frac {b}{R}}.}$

Это равенство может быть выведено как особый случай сферической теоремы косинусов, которая справедлива для всех сферических треугольников:

${displaystyle cos {frac {c}{R}}=cos {frac {a}{R}}cdot cos {frac {b}{R}}+sin {frac {a}{R}}cdot sin {frac {b}{R}}cdot cos gamma .}$

Применяя ряд Тейлора в функции косинуса ( ${displaystyle cos xapprox 1-{dfrac {x^{2}}{2}}}$ ) можно показать, что если радиус стремится к бесконечности, а аргументы ${displaystyle {dfrac {a}{R}}}$ , ${displaystyle {dfrac {b}{R}}}$ и ${displaystyle {dfrac {c}{R}}}$ стремятся к нулю, то сферическое соотношение между сторонами в прямоугольном треугольнике приближается к теореме Пифагора.

Геометрия Лобачевского[править | править код]

В геометрии Лобачевского для прямоугольного треугольника со сторонами a,b,c со стороной , противолежащей прямому углу, соотношение между сторонами будет следующим^[29]:

{displaystyle operatorname {ch} c=operatorname {ch} acdot operatorname {ch} b}

где — гиперболический косинус^[30]. Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников^[31]:

{displaystyle operatorname {ch} c=operatorname {ch} acdot operatorname {ch} b-operatorname {sh} acdot operatorname {sh} bcdot cos gamma }

где gamma — угол, вершина которого противоположна стороне .

Используя ряд Тейлора для гиперболического косинуса ( ${displaystyle operatorname {ch} xapprox 1+{dfrac {x^{2}}{2}}}$ ) можно показать, что если гиперболический треугольник уменьшается (то есть, когда , и стремятся к нулю), то гиперболические соотношения в прямоугольном треугольнике приближаются к соотношению классической теоремы Пифагора.

Применение[править | править код]

Расстояние в двумерных прямоугольных системах[править | править код]

Важнейшее применение теоремы Пифагора — определение расстояния между двумя точками в прямоугольной системе координат: расстояние между точками с координатами (a, b) и равно

${displaystyle s={sqrt {(a-c)^{2}+(b-d)^{2}}}.}$

Для комплексных чисел теорема Пифагора даёт естественную формулу для нахождения модуля комплексного числа — для он равен длине радиус-вектора на комплексной плоскости к точке (x, y) :

${displaystyle |z|={sqrt {x^{2}+y^{2}}}.}$

Расстояние между комплексными числами ${displaystyle z_{1}=x_{1}+y_{1}i}$ и ${displaystyle z_{2}=x_{2}+y_{2}i}$ также представляется в форме теоремы Пифагора^[32]:

${displaystyle |z_{1}-z_{2}|={sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}$

Расстояние между двумя точками в плоскости Лобачевского[править | править код]

$ds^{2}=dx^{2}+operatorname {ch} ^{2}left({frac {y}{R}}right)dy^{2}$ .

Здесь R — радиус кривизны плоскости Лобачевского, ch — гиперболический косинус.

Евклидова метрика[править | править код]

Евклидова метрика — функция расстояния в евклидовых пространствах, определяемая по теореме Пифагора, непосредственным её применением в двумерном случае, и последовательным в многомерном; для точек -мерного пространства ${displaystyle p=(p_{1},dots ,p_{n})}$ и ${displaystyle q=(q_{1},dots ,q_{n})}$ расстояние между ними определяется следующим образом:

${displaystyle d(p,q)={sqrt {sum _{i=1}^{n}{(p_{i}-q_{i})^{2}}}}}$

Теория чисел[править | править код]

Пифагорова тройка — набор из трёх натуральных чисел , которые могут быть длинами сторон прямоугольного треугольника, то есть натуральные числа, удовлетворяющие диофантову уравнению $x^{2}+y^{2}=z^{2}$ . Пифагоровы тройки играют важную роль в теории чисел, задача их эффективного нахождения породила широкий пласт работ, начиная с древнейших времён и вплоть до современности. Формулировка Великой теоремы Ферма аналогична задаче нахождения пифагоровых троек для степени более 2.

Единственная пифагорова тройка, состоящая из трёх последовательных чисел — это 3, 4 и 5: ${displaystyle 3^{2}+4^{2}=5^{2}}$ ^[33].

В массовой культуре[править | править код]

С одним из изображений доказательства теоремы связано популярное в русском школьном фольклоре выражение «Пифагоровы штаны на все стороны равны», получившее особенную известность благодаря комической опере 1915 года «Иванов Павел»^[34]^[35].

Примечания[править | править код]

↑ Кантор ссылается на папирус 6619 Берлинского музея
↑ History topic: Pythagoras’s theorem in Babylonian mathematics. Дата обращения: 1 июня 2009. Архивировано 6 июня 2011 года.
↑ Наука, техническая и военная мысль, здравоохранение и образование // Духовная культура Китая: энциклопедия в 5 томах / Титаренко М. Л. — М.: Восточная литература РАН, 2009. — Т. 5. — С. 939—941. — 1055 с. — ISBN 9785020184299. Архивная копия от 4 марта 2016 на Wayback Machine
↑ Euclid, 1956, p. 351.
↑ Heath, 1921, vol I, p. 144.
↑ Kurt Von Fritz. The Discovery of Incommensurability by Hippasus of Metapontum (англ.) // The Annals of Mathematics, Second Series : journal. — Annals of Mathematics, 1945. — April (vol. 46, no. 2). — P. 242—264. — JSTOR 1969021.: «Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики».
↑ Георг Гегель. Лекции по истории философии. — Litres, 2016-09-08. — С. 282. — 1762 с. — ISBN 9785457981690.
↑ Asger Aaboe. Episodes from the early history of mathematics (англ.). — Mathematical Association of America, 1997. — P. 51. — ISBN 0883856131. Архивная копия от 9 августа 2016 на Wayback Machine. — «…it is not until Euclid that we find a logical sequence of general theorems with proper proofs.».
↑ Шахмейстер А. Х. Треугольники и параллелограммы // Геометрические задачи на экзаменах. Часть 1. Планиметрия : книга / А. Х. Шахмейстер. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2015. — С. 102. — 392 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512^(G). — ISBN 978-5-98712-083-5. — ISBN 978-5-91673-155-2. — ISBN 978-5-4439-0347-7.
↑ Тимофеева И. Л. Глава 3. Математические определения и теоремы и их строение (п. 3.3. Обратная теорема) // Вводный курс математики: учебное пособие для студентов учреждений высш. пед. проф. образования / И. Л. Тимофеева, И. Е. Сергеева, Е. В. Лукьянова; под ред. В. Л. Матросова. — М.: Издательский центр «Академия», 2011. — С. 134—136. — 240 с. — ISBN 978-5-7695-7960-8, ББК 22.1я73, УДК 51 (075.8).
↑ Elisha Scott Loomis. Pythagorean Proposition
↑ См. например Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 196.
↑ См. например Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 259.
↑ Franz Lemmermeyer. Leonardo da Vinci’s Proof of the Pythagorean Theorem (англ.). The College Mathematics Journal 47(5):361 (ноябрь 2016). Дата обращения: 22 октября 2021. Архивировано 7 июня 2022 года.
↑ См. например Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 263.
↑ Euclid’s Elements: book VI, proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle».
↑ Lawrence S. Leff. Cited work. — Barron’s Educational Series, 2005. — С. 326. — ISBN 0764128922.
↑ Howard Whitley Eves. § 4.8: …generalization of Pythagorean theorem // Great moments in mathematics (before 1650) (англ.). — Mathematical Association of America, 1983. — P. 41. — ISBN 0883853108. Архивная копия от 9 августа 2016 на Wayback Machine
↑ Aydin Sayili. Thâbit ibn Qurra’s Generalization of the Pythagorean Theorem (англ.) // Isis : journal. — 1960. — March (vol. 51, no. 1). — P. 35—37. — doi:10.1086/348837. — JSTOR 227603.
↑ Judith D. Sally, Paul Sally. Exercise 2.10 (II) // Cited work. — 2007. — С. 62. — ISBN 0821844032. Архивная копия от 9 августа 2016 на Wayback Machine
↑ George Jennings. Figure 1.32: The generalized Pythagorean theorem // Modern geometry with applications: with 150 figures (англ.). — 3rd. — Springer (англ.) (рус., 1997. — P. 23. — ISBN 038794222X.
↑
Rajendra Bhatia. Matrix analysis. — Springer (англ.) (рус., 1997. — С. 21. — ISBN 0387948465.
↑ Шилов Г. Е. Математический анализ. Специальный курс. — М.: Физматлит, 1961. — C. 194
↑ Stephen W. Hawking. Cited work. — 2005. — С. 4. — ISBN 0762419229. Архивная копия от 17 августа 2016 на Wayback Machine
↑ Eric W. Weisstein. CRC concise encyclopedia of mathematics. — 2nd. — 2003. — С. 2147. — ISBN 1584883472. Архивная копия от 17 августа 2016 на Wayback Machine. — «The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.».
↑ Alexander R. Pruss. The principle of sufficient reason: a reassessment (англ.). — Cambridge University Press, 2006. — P. 11. — ISBN 052185959X. Архивная копия от 9 августа 2016 на Wayback Machine. — «We could include… the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.».
↑ Victor Pambuccian. Maria Teresa Calapso’s Hyperbolic Pythagorean Theorem (англ.) // The Mathematical Intelligencer : journal. — 2010. — December (vol. 32). — P. 2. — doi:10.1007/s00283-010-9169-0.
↑ Barrett O’Neill. Exercise 4 // Elementary differential geometry. — 2nd. — Academic Press, 2006. — С. 441. — ISBN 0120887355.
↑ Saul Stahl. Theorem 8.3 // The Poincaré half-plane: a gateway to modern geometry (англ.). — Jones & Bartlett Learning (англ.) (рус., 1993. — P. 122. — ISBN 086720298X.
↑ Микиша А. М., Орлов В. Б. Толковый математический словарь. Основные термины. — М. Русский язык, 1989 г.
↑ Jane Gilman. Hyperbolic triangles // Two-generator discrete subgroups of PSL (2, R) (англ.). — American Mathematical Society Bookstore, 1995. — ISBN 0821803611.
↑ Alfred Gray, Elsa Abbena, Simon Salamon. Modern differential geometry of curves and surfaces with Mathematica (англ.). — 3rd. — CRC Press, 2006. — P. 194. — ISBN 1584884487.
↑ Siegel E. This One Equation, 10² + 11² + 12² = 13² + 14², Takes Pythagoras To A Whole New Level (англ.). Forbes (6 марта 2020). Дата обращения: 28 апреля 2020. Архивировано 4 апреля 2020 года.
↑ Легендарная опера: текст и ноты. LiveJournal (4 августа 2016). Дата обращения: 9 января 2020. Архивировано 9 июня 2020 года.
↑ Словарь современных цитат. Litres, 20 мар. 2019 г. С. 9.

Литература[править | править код]

Ван-дер-Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — М., 1959.
Глейзер Г. И. История математики в школе. — М., 1982.
Еленьский Щ. По следам Пифагора. — М.: Детгиз, 1961. — 486 с. : ил., карт.
Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5). — ISBN 978-5-9774-0633-8.
Литцман В. Теорема Пифагора. — М., 1960.
- Сайт о теореме Пифагора с большим числом доказательств, материал взят из книги В. Литцмана, большое число чертежей представлено в виде отдельных графических файлов.
Скопец З. А. Геометрические миниатюры. — М., 1990
Euclid. The Elements (3 vols.) / Translated by Johan Ludvig Heiberg with an introduction and commentary by Thomas L. Heath. — Reprint of 1908. — Dover, 1956. — Vol. 1 (Books I and II). — ISBN 0-486-60088-2.
Heath S. A History of Greek Mathematics (2 Vols.). — Edition of Dover Publications, Inc. (1981). — Clarendon Press, Oxford, 1921. — ISBN 0-486-24073-8.

Ссылки[править | править код]

История теоремы Пифагора
Глейзер Г., академик РАО, Москва. О теореме Пифагора и способах её доказательства
Ролик серии «Математические этюды», посвящённый теореме Пифагора (для компьютера, iPhone, iPad)
Теорема Пифагора и пифагоровы тройки. Архивная копия от 3 марта 2016 на Wayback Machine Глава из книги Д. В. Аносова «Взгляд на математику и нечто из неё»
Теорема Пифагора на WolframMathWorld (англ.)
Cut-The-Knot, секция, посвящённая теореме Пифагора, около 70 доказательств и обширная дополнительная информация (англ.)

Источник

Теорема пифагора

Определение теоремы пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обозначив гипотенузу буквой – c, катеты буквами a и b получим следующее равенство

c²=a²+b²

Расчёт катета по теореме пифагора

Введите гипотенузу

c =

Введите катет

b =

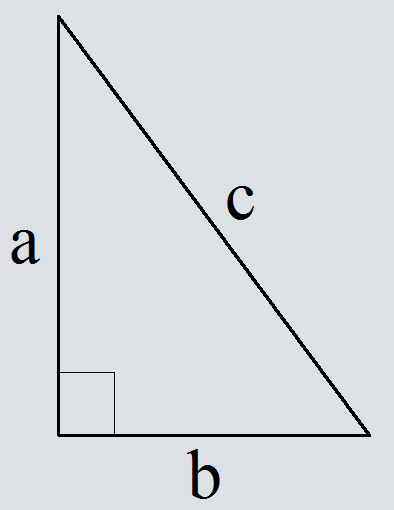
Формула пифагора для катета

Где a, b – катеты прямоугольного треугольника,
с – гипотенуза прямоугольного треугольника

Расчёт гипотенузы по теореме пифагора

Введите первый катет

a =

Введите второй катет

b =

Формула пифагора для гипотенузы

Где a, b – катеты прямоугольного треугольника,
с – гипотенуза прямоугольного треугольника

Доказательство теоремы пифагора

Дано

Прямоугольный треугольник с катетами a, b и гипотенузой c.

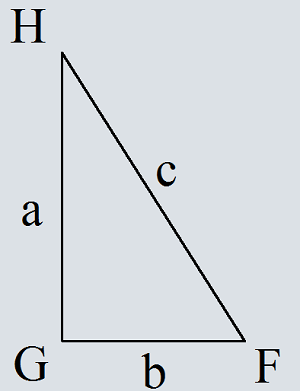
Доказать

c²=a²+b²

Доказательство

Достроим треугольник HFG до квадрата со стороной a+b.

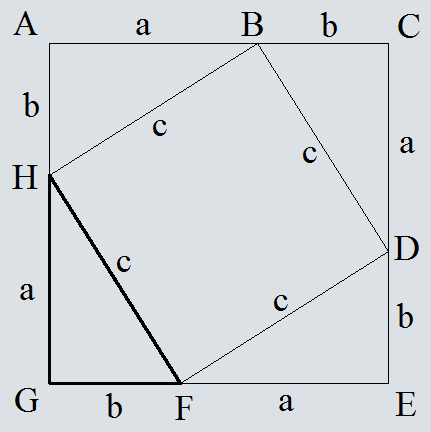
Запишем площадь получевшегося квадрата двумя способами

S=(a+b)²

S=4*0.5*a*b +c²

Приравняем площади

(a+b)²=4*0.5*a*b +c²

a²+2*a*b +b²=2*a*b +c²

a²+b²=c²

Теорема доказана

Источник

Теорема Пифагора

О важности теоремы Пифагора высказался Иоганн Кеплер: «Геометрия обладает двумя великими сокровищами: теоремой Пифагора и делением отрезка в крайнем и среднем отношении; первое можно сравнить с мерой золота, второе назвать драгоценным камнем»

Теорема Пифагора. Фото: Liza Summer, pixals.com

Теорема Пифагора актуальна в заданиях как базового, так и профильного ЕГЭ по математике. За верное решение задач базового уровня дается 1 балл, за задания повышенного уровня начисляется 3 балла. В статье мы рассмотрим доказательство теоремы и решим пару задач по теме. Благодаря качественному изучению этого материала экзаменуемый справится с рядом заданий и получит за них наивысший балл.

Что такое теорема Пифагора

Теорема Пифагора устанавливает соотношение между сторонами прямоугольного треугольника. Изображение: Наталия Юмагулова.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Важно!

Сторону прямоугольного треугольника, противолежащую прямому углу, называют гипотенузой, а стороны, прилежащие к прямому углу, — катетами. Гипотенуза больше любого из катетов («Геометрия. 8 класс. Учебник», А. Г. Мерзляк).

Формула теоремы Пифагора

c² = a² + b²

Из этой формулы выводятся следующие:

с = √a² + b²

a = √c² — b²

b = √c² — a²

Доказательство теоремы Пифагора

В литературе есть около 400 доказательств теоремы Пифагора

Дано:
△АВС — прямоугольный;
＜АСВ = 90⁰.

Доказать:
АВ² = АС² + ВС².

Доказательство:
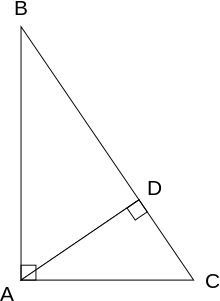
Проведем высоту СН.

АН, НВ — проекции катетов АС и ВС на гипотенузу. По теореме о метрических соотношениях в прямоугольном треугольнике, квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу. Значит,

АС² = АВ × АН; ВС² = АВ × НВ.

Сложим почленно эти равенства:

АС² + ВС² = АВ × АН + АВ × НВ = АВ × (АН + НВ) = АВ ×АВ = АВ².

Что и требовалось доказать.

Задачи на теорему Пифагора

Переходим к решению задач с помощью теоремы Пифагора.

Задача №1
Центр окружности, описанной около треугольника КРH, лежит на стороне КН. Радиус окружности равен 10. Найдите КР, если РН равен 12

Дано:
Описанная окружность с центром в точке О.
О ∈ КН;
R = 10;
РН = 12.

Найти: КР.

Решение:
Так как окружность описанная, то все вершины треугольника лежат на ней. Следовательно, угол ＜КРН — вписанный.

По условию задачи центр окружности О ∈ КН, значит, хорда КН является диаметром.

КН = 2R = 2 ✕ 10 = 20.

Вписанный угол ＜КРН, опирающийся на диаметр, — прямой, значит, треугольник КРН — прямоугольный.

По теореме Пифагора:

КР = √КН² — РН²,
КР = √400-144 = √256 = 16

Ответ: КР = 16

Теорема о трех перпендикулярах

Доказательство и формулировка теоремы о трех перпендикулярах

подробнее

Задача №2

Дано:
Пирамида МАВС с высотой МА. Известно, что в основании лежит прямоугольный треугольник с прямым углом С.

Найти:
1) Угол между ребрами МС и ВС. Ответ дайте в градусах.
2) МВ, если МС = 12, ВС = 5.

Решение:
1) Так как по условию задачи МА — высота пирамиды, то МА ⟂ (АВС). АС — проекция наклонной МС на плоскость АВС. Так как АС ⟂ ВС, то, по теореме о трех перпендикулярах, МС ⟂ ВС, следовательно, угол между МС и ВС равен 90° (градусов).

Ответ: 90°.

2) Так как из пункта 1 МС ⟂ ВС ⇒ треугольник МСВ — прямоугольный ⇒ по теореме Пифагора: МВ = √МС² + ВС² ⇒ МВ = √144 + 25 = √169 = 13.

Ответ: МВ = 13.

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х². Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с²– это площадь большого (на рисунке – синего)квадрата, а х² – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

10:2 = 5

Другой катет находим с помощью теоремы Пифагора:

Задачи на применение теоремы Пифагора

Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.

Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.

Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.

Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.

Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.

Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Пифагоровы тройки

Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.

Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.

Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.

Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.

Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.

Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.

Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а², b²и с² – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а² + b²четное. Таким образом, получается, что равенство

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.

Обратная теорема Пифагора

По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:

Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.

Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство

Так как ∆А₁В₁С₁ прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:

а именно это мы и доказываем.

Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:

1) некоторое условие, которое описывает какое-то геометрическое построение;

2) вывод (или заключение), который делается для условия.

В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.

В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.

Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.

Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:

Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.

Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.

Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:

Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда

Формула Герона

Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.

Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:

По рисунку можно записать три уравнения:

Левая часть одинакова в обоих уравнениях, значит, равны и правые:

С учетом этого выразим h²:

Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть

Площадь треуг-ка вычисляется по формуле:

Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.

Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?

Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:

Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.

Источник

Пифагор ((570)–(490) года до н. э.) – древнегреческий математик, мыслитель и философ.

Рис. (1). Пифагор.

Факты биографии Пифагора достоверно не известны. О его жизненном пути можно судить лишь по произведениям других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учёными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства.

Философия Пифагора, его образ жизни привлекли многих последователей, но у философа и учёного было и много противников.
Как математик Пифагор достиг больших успехов. Одна из самых известных геометрических теорем — теорема Пифагора, ему приписывают открытие и доказательство теоремы, создание таблицы Пифагора.

Рис. (2). Теорема Пифагора.

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, например, древние египтяне знали о том, что треугольник со сторонами (3), (4) и (5) является прямоугольным.

В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):

Рис. (3). Прямоугольный треугольник.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

c2=a2+b2

Известны очень многие доказательства теоремы разными математическими методами, но одни из самых наглядных связаны с площадями.

1. Построим квадрат, сторона которого равна сумме катетов данного треугольника

a+b

. Площадь квадрата равна

a+b2

Рис. (4). Первое доказательство теоремы Пифагора.

2. Если провести гипотенузы (c), очевидно, что они образовали квадрат внутри построенного квадрата.

Стороны четырёхугольника равны (c), а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают

90°

, то угол четырёхугольника также равен

90°

, потому что вместе все три угла дают

180°

Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами.

Рис. (5). Второе доказательство теоремы Пифагора.

3. На двух сторонах квадрата поменяем местами отрезки (a) и (b), при этом длина стороны квадрата не меняется.

Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами (a) и (b), и двух площадей прямоугольников:

Рис. (6). Третье доказательство теоремы Пифагора.

4. Из этого следуют выводы:

c2+4⋅ab2=(a+b)2;c2+2ab=a2+2ab+b2;

Обрати внимание!

Если находим длину гипотенузы (c), то выполняем сложение квадратов длин катетов (a) и (b) и определяем квадратный корень:

c2=a2+b2;c=a2+b2.

Если находим длину одного катета, то выполняем вычитание длины квадрата другого катета из квадрата длины гипотенузы и определяем квадратный корень:

a2=c2−b2;a=c2−b2.

Обратная теорема используется как признак прямоугольного треугольника.

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.

Пример:

является ли треугольник со сторонами (6) см, (7) см и (9) см прямоугольным?

Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:

92=62+72;81≠36+49

— значит, этот треугольник не прямоугольный.

Является ли треугольник со сторонами (5) см, (12) см и (13) см прямоугольным?

Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:

132=122+52;169=144+25

— значит, этот треугольник прямоугольный.

Чтобы не тратить много времени на решение, полезно запомнить наиболее часто используемые числа Пифагора:

катет, катет, гипотенуза

(3), (4), (5);

(6), (8), (10);

(12), (16), (20);

(5), (12), (13).

Посмотри ещё одно своеобразное доказательство теоремы Пифагора:

Рис. (7). Четвёртое доказательство теоремы Пифагора.

Источники:

Рис. 2. Теорема Пифагора. Указание авторства не требуется, 2021-06-05, Наука/Технологии, бесплатно для коммерческого использования, https://clck.ru/VK55r.

Рис. 7. Четвёртое доказательство теоремы Пифагора, http://linguaggio-macchina.blogspot.com

Источник

История[править | править код]

Формулировки[править | править код]

Доказательства[править | править код]

Через подобные треугольники[править | править код]

Доказательства методом площадей[править | править код]

Доказательство через равнодополняемость[править | править код]

Доказательство Евклида[править | править код]

Доказательство Леонардо да Винчи[править | править код]

Через площади подобных треугольников[править | править код]

Доказательство методом бесконечно малых[править | править код]

Вариации и обобщения[править | править код]

Подобные геометрические фигуры на трёх сторонах[править | править код]

Теорема косинусов[править | править код]

Произвольный треугольник[править | править код]

Теорема Паппа о площадях[править | править код]

Многомерные обобщения[править | править код]

Неевклидова геометрия[править | править код]

Сферическая геометрия[править | править код]

Геометрия Лобачевского[править | править код]

Применение[править | править код]

Расстояние в двумерных прямоугольных системах[править | править код]

Расстояние между двумя точками в плоскости Лобачевского[править | править код]

Евклидова метрика[править | править код]

Теория чисел[править | править код]

В массовой культуре[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Теорема пифагора

Определение теоремы пифагора

Расчёт катета по теореме пифагора

Формула пифагора для катета

Расчёт гипотенузы по теореме пифагора

Формула пифагора для гипотенузы

Доказательство теоремы пифагора

Теорема Пифагора

Что такое теорема Пифагора

Формула теоремы Пифагора

Доказательство теоремы Пифагора

Задачи на теорему Пифагора

Популярные вопросы и ответы

Почему теорему Пифагора изучают на геометрии в 8 классе?

Где и когда возникла теорема Пифагора?

Где в жизни можно применить теорему Пифагора?

Как звучит обратная теорема Пифагора?

Теорема Пифагора

Задачи на применение теоремы Пифагора

Пифагоровы тройки

Обратная теорема Пифагора

Формула Герона

Вам также может понравиться

Как найти целую часть от дроби правило

Как найти цену товара за килограмм

Как найти девушку которую я поссорился

Добавить комментарий Отменить ответ