Теоретическая сложность алгоритма как найти

Алгоритм — это точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату [1].

При разработке алгоритмов очень важно иметь возможность оценить ресурсы, необходимые для проведения вычислений, результатом оценки является функция сложности (трудоемкости). Оцениваемым ресурсом чаще всего является процессорное время (вычислительная сложность) и память (сложность алгоритма по памяти). Оценка позволяет предсказать время выполнения и сравнивать эффективность алгоритмов.

Содержание:

1. Модель RAM (Random Access Machine)
2. Подсчет операций. Классы входных данных
3. Асимптотические обозначения
4. Примеры анализа алгоритмов
5. Математический аппарат анализа алгоритмов
   1. Формулы суммирования
   2. Суммирование и интегрирование
   3. Сравнение сложности алгоритмов. Пределы
   4. Логарифмы и сложность алгоритмов
6. Результаты анализа. Замечания. Литература

Модель RAM (Random Access Machine)

Каждое вычислительное устройство имеет свои особенности, которые могут влиять на длительность вычисления. Обычно при разработке алгоритма не берутся во внимание такие детали, как размер кэша процессора или тип многозадачности, реализуемый операционной системой. Анализ алгоритмов проводят на модели абстрактного вычислителя, называемого машиной с произвольным доступом к памяти (RAM).

Модель состоит из памяти и процессора, которые работают следующим образом:

• память состоит из ячеек, каждая из которых имеет адрес и может хранить один элемент данных;
• каждое обращение к памяти занимает одну единицу времени, независимо от номера адресуемой ячейки;
• количество памяти достаточно для выполнения любого алгоритма;
• процессор выполняет любую элементарную операцию (основные логические и арифметические операции, чтение из памяти, запись в память, вызов подпрограммы и т.п.) за один временной шаг;
• циклы и функции не считаются элементарными операциями.

Несмотря на то, что такая модель далека от реального компьютера, она замечательно подходит для анализа алгоритмов. После того, как алгоритм будет реализован для конкретной ЭВМ, вы можете заняться профилированием и низкоуровневой оптимизацией, но это будет уже оптимизация кода, а не алгоритма.

Подсчет операций. Классы входных данных

Одним из способов оценки трудоемкости ((T_n)) является подсчет количества выполняемых операций. Рассмотрим в качестве примера алгоритм поиска минимального элемента массива.

начало; поиск минимального элемента массива array из N элементов
min := array[1]
для i от 2 до N выполнять:
  если array[i] < min
    min := array[i]
конец; вернуть min

При выполнении этого алгоритма будет выполнена:

1. N — 1 операция присваивания счетчику цикла i нового значения;
2. N — 1 операция сравнения счетчика со значением N;
3. N — 1 операция сравнения элемента массива со значением min;
4. от 1 до N операций присваивания значения переменной min.

Точное количество операций будет зависеть от обрабатываемых данных, поэтому имеет смысл говорить о наилучшем, наихудшем и среднем случаях. При этом худшему случаю всегда уделяется особое внимание, в том числе потому, что «плохие» данные могут быть намеренно поданы на вход злоумышленником.

Понятие среднего случая используется для оценки поведения алгоритма с расчетом на то, что наборы данных равновероятны. Однако, такая оценка достаточно сложна:

1. исходные данные разбиваются на группы так, что трудоемкость алгоритма ((t_i)) для любого набора данных одной группы одинакова;
2. исходя из доли наборов данных группы в общем числе наборов, рассчитывается вероятность для каждой группы ((p_i));
3. оценка среднего случая вычисляется по формуле: (sumlimits_{i=1}^m p_icdot t_i).

Асимптотические обозначения

Подсчет количества операций позволяет сравнить эффективность алгоритмов. Однако, аналогичный результат можно получить более простым путем. Анализ проводят с расчетом на достаточно большой объем обрабатываемых данных (( n to infty )), поэтому ключевое значение имеет скорость роста функции сложности, а не точное количество операций.

При анализе скорости роста игнорируются постоянные члены и множители в выражении, т.е. функции (f_x = 10 cdot x^2 + 20 ) и ( g_x = x^2) эквивалентны с точки зрения скорости роста. Незначащие члены лишь добавляют «волнистости», которая затрудняет анализ.

В оценке алгоритмов используются специальные асимптотические обозначения, задающие следующие классы функций:

• (mathcal{O}(g)) — функции, растущие медленнее чем g;
• (Omega(g)) — функции, растущие быстрее чем g;
• (Theta(g)) — функции, растущие с той же скоростью, что и g.

Запись (f_n = mathcal{O}(g_n)) означает принадлежность функции f классу (mathcal{O}(g)), т.е. функция f ограничена сверху функцией g для достаточно больших значений аргумента. (exists n_0 > 0, c > 0 : forall n > n_0, f_n leq c cdot g_n).

Ограниченность функции g снизу функцией f записывается следующим образом: (g_n =Omega(f_n)). Нотации (Omega) и (mathcal{O}) взаимозаменяемы: (f_n = mathcal{O}(g_n) Leftrightarrow g_n =Omega(f_n)).

Если функции f и g имеют одинаковую скорость роста ((f_n = Theta(g_n))), то существуют положительные константы (c_1) и (c_2) такие, что (exists n_0 > 0 : forall n > n_0, f_n leq c_1 cdot g_n, f_n geq c_2 cdot g_n). При этом (f_n = Theta(g_n) Leftrightarrow g_n = Theta(f_n)).

Примеры анализа алгоритмов

Алгоритм поиска минимального элемента массива, приведенный выше, выполнит N итераций цикла. Трудоемкость каждой итерации не зависит от количества элементов массива, поэтому имеет сложность (T^{iter} = mathcal{O}(1)). В связи с этим, верхняя оценка всего алгоритма (T^{min}_n = mathcal{O}(n) cdot mathcal{O}(1) = mathcal{O}(n cdot 1) = mathcal{O}(n)). Аналогично вычисляется нижняя оценка сложности, а в силу того, что она совпадает с верхней — можно утверждать (T^{min}_n = Theta(n) ).

Алгоритм пузырьковой сортировки (bubble sort) использует два вложенных цикла. Во внутреннем последовательно сравниваются пары элементов и если оказывается, что элементы стоят в неправильном порядке — выполняется перестановка. Внешний цикл выполняется до тех пор, пока в массиве найдется хоть одна пара элементов, нарушающих требуемый порядок [2].

начало; пузырьковая сортировка массива array из N элементов
nPairs := N; количество пар элементов
hasSwapped := false; пока что ни одна пара не нарушила порядок
для всех i от 1 до nPairs-1 выполнять:
  если array[i] > array[i+1] то:
    swap(array[i], array[i+1]); обменять элементы местами
    hasSwapped := true; найдена перестановка
  nPairs := nPairs - 1; наибольший элемент гарантированно помещен в конец
 если hasSwapped = true - то перейти на п.3
 конец; массив array отсортирован

Трудоемкость функции swap не зависит от количества элементов в массиве, поэтому оценивается как (T^{swap} = Theta(1) ). В результате выполнения внутреннего цикла, наибольший элемент смещается в конец массива неупорядоченной части, поэтому через N таких вызовов массив в любом случае окажется отсортирован. Если же массив отсортирован, то внутренний цикл будет выполнен лишь один раз.

Таким образом:

• (T^{bubble}_n = mathcal{O}(sumlimits_{i=1}^n sumlimits_{j=1}^{n-i} 1) = mathcal{O}(sumlimits_{i=1}^n n) = mathcal{O}(n ^2));
• (T^{bubble}_n = Omega(1 cdot sumlimits_{j=1}^{n-i} 1) = Omega(n)).

В алгоритме сортировки выбором массив мысленно разделяется на упорядоченную и необработанную части. На каждом шаге из неупорядоченной части массива выбирается минимальный элемент и добавляется в отсортированную часть [2].

начало; selection_sort - сортировка массива array из N элементов методом выбора
для всех i от 1 до N выполнять:
  imin := indMin(array, N, i)
  swap(array[i], array[imin])
конец; массив array отсортирован

Для поиска наименьшего элемента неупорядоченной части массива используется функция indMin, принимающая массив, размер массива и номер позиции, начиная с которой нужно производить поиск. Анализ сложности этой функции можно выполнить аналогично тому, как это сделано для функции min — количество операций линейно зависит от количества обрабатываемых элементов: ( T^{indMin}_{n, i} = Theta(n — i)).

У сортировки выбором нет ветвлений, которые могут внести различия в оценку наилучшего и наихудшего случаев, ее трудоемкость: (T^{select}_n = Theta(sumlimits_{i=1}^{n} (T^{indMin}_{n, i} + T^{swap})) =Theta(sumlimits_{i=1}^{n} (n-i)) = Theta(frac{n-1}{2} cdot n) = Theta(n^2) ).

Математический аппарат анализа алгоритмов

Выше были рассмотрены асимптотические обозначения, используемые при анализе скорости роста. Они позволяют существенно упростить задачу отбросив значительную часть выражения. Однако, в математическом анализе имеется целый ворох таких приемов.

Формулы суммирования

В примерах, рассмотренных выше, мы уже сталкивались с нетривиальными формулами суммирования. Чтобы дать оценку суммы можно использовать ряд известных тождеств:

• вынос постоянного множителя за знак суммы: (sumlimits_{i=1}^{n} (c cdot f_i) = c cdot sumlimits_{i=1}^{n} cdot f_i);
• упрощение суммы составного выражения: (sumlimits_{i=1}^{n} (f_i + g_i) = sumlimits_{i=1}^{n} (f_i) + sumlimits_{i=1}^{n} (g_i));
• сумма чисел арифметической прогрессии: (sumlimits_{i=1}^{n} (i^p) = Theta(n^{p+1}));
• сумма чисел геометрической прогрессии: (sumlimits_{i=0}^{n} (a^i) = frac {a cdot (a^{n+1} — 1)}{a — 1}). При ( n to infty ) возможны 2 варианта:
  • если a < 1, то сумма стремится к константе: (Theta(1));
  • если a > 1, то сумма стремится к бесконечности: (Theta(a^{n+1}));
  • если a = 0, формула неприменима, сумма стремится к N: (Theta(n));
• логарифмическая сложность алгоритма: (sumlimits_{i=1}^{n} frac{1}{i} = Theta(log n));
• сумма логарифмов: (sumlimits_{i=1}^{n} log i = Theta(n cdot log n)).

Первые из этих тождеств достаточно просты, их можно вывести используя метод математической индукции. Если под знаком суммы стоит более сложная формула, как в двух последних тождествах — суммирование можно заменить интегрированием (взять интеграл функции гораздо проще, ведь для этого существует широкий спектр приемов).

Суммирование и интегрирование

Известно, что интеграл можно понимать как площадь фигуры, размещенной под графиком функции. Существует ряд методов аппроксимации (приближенного вычисления) интеграла, к ним относится, в частности, метод прямоугольников. Площадь под графиком делится на множество прямоугольников и приближенно вычисляется как сумма их площадей. Следовательно, возможен переход от интеграла к сумме и наоборот.

На рисунках приведен пример аппроксимации функции (f_x = log x) левыми и правыми прямоугольниками. Очевидно, они дадут верхнюю и нижнюю оценку площади под графиком:

• (intlimits_a^n f_x dx leq sumlimits_{i=a }^{n} f_i leq intlimits_{a+1}^{n+1} f_x dx) для возрастающих функций;
• (intlimits_a^n f_x dx geq sumlimits_{i=a }^{n} f_i geq intlimits_{a+1}^{n+1} f_x dx) для убывающих функций.

В частности, такой метод позволяет оценить алгоритмы, имеющие логарифмическую сложность (две последние формулы суммирования).

Сравнение сложности алгоритмов. Пределы

Сложность алгоритмов определяется для больших объемов обрабатываемых данных, т.е. при (ntoinfty). В связи с этим, при сравнении трудоемкости двух алгоритмов можно рассмотреть предел отношения функций их сложности: (limlimits_{n to infty} frac {f_n}{g_n}). В зависимости от значения предела возможно сделать вывод относительно скоростей роста функций:

• предел равен константе и не равен нулю, значит функции растут с одной скоростью:(f_n = Theta(g_n));
• предел равен нулю, следовательно (g_n) растет быстрее чем (f_n): (f_n = mathcal{O}(g_n));
• предел равен бесконечности, (g_n) растет медленнее чем (f_n): (f_n = Omega(g_n)).

Если функции достаточно сложны, то такой прием значительно упрощает задачу, т.к. вместо предела отношения функций можно анализировать предел отношения их производных (согласно правилу Лопиталя): (limlimits_{n to infty} frac {f_n}{g_n} = limlimits_{n to infty} frac {f’_n}{g’_n}). Правило Лопиталя можно использовать если функции обладают следующими свойствами:

• (limlimits_{n to infty} frac {f_n}{g_n} = frac{0}{0} или frac {infty}{infty} );
• ( f_n ) и (g_n) дифференцируемы;
• ( g’_n ne 0 ) при (n to infty);
• (exists limlimits_{n to infty} frac {f’_n}{g’_n}).

Допустим, требуется сравнить эффективность двух алгоритмов с оценками сложности (mathcal{O}(a^n)) и (mathcal{O}(n^b)), где a и b — константы. Известно, что ((c^x)’ =c^x cdot ln(c)), но ((x^c)’ = c cdot x^{c-1} ). Применим правило Лопиталя к пределу отношения наших функций b раз, получим: (limlimits_{n to infty} frac {mathcal{O}(a^n)}{mathcal{O}(n^b)} = limlimits_{n to infty} frac {mathcal{O}(a^n * ln^b (a))}{mathcal{O}(b!)} = infty). Значит функция (a^n) имеет более высокую скорость роста. Без использования пределов и правила Лопиталя такой вывод может казаться не очевидным.

Логарифмы и сложность алгоритмов. Пример

По определению (log_a{x} = b Leftrightarrow x = a^b). Необходимо знать, что (x to infty Rightarrow log_a{x} to infty), однако, логарифм — это очень медленно растущая функция. Существует ряд формул, позволяющих упрощать выражения с логарифмами:

• (log_a{x cdot y} = log_a{x} + log_a{ y});
• (log_a{x^b} = b cdot log_a{ x});
• (log_a{x} =frac{log_b{x}}{log_b{a}}).

При анализе алгоритмов обычно встречаются логарифмы по основанию 2, однако основание не играет большой роли, поэтому зачастую не указывается. Последняя формула позволяет заменить основание логарифма, домножив его на константу, но константы отбрасываются при асимптотическом анализе.

Логарифмической сложностью обладают алгоритмы, для которых не требуется обрабатывать все исходные данные, они используют принцип «разделяй и властвуй». На каждом шаге часть данных (обычно половина) отбрасывается. Примером может быть функция поиска элемента в отсортированном массиве (двоичного поиска):

начало; поиск элемента E в отсортированном по возрастанию массиве array из N элементов
left := 1, right := N; левая и правая граница, в которых находится искомый элемент
выполнять пока left =< right:
  mid := (right + left) div 2; вычисление индекса элемента посередине рассматриваемой части массива
  если array[mid] = E
    конец; вернуть true (элемент найден)
  если array[mid] < E; искомый элемент больше середины, значит все элементы левее mid можно отбросить
    left := mid + 1;
  иначе
    right := mid
конец; вернуть false (элемент не найден)

Очевидно, что на каждом шаге алгоритма количество рассматриваемых элементов сокращается в 2 раза. Количество элементов, среди которых может находиться искомый, на k-том шаге определяется формулой (frac{n}{2^k}). В худшем случае поиск будет продолжаться пока в массиве не останется один элемент, т.е. чтобы определить количество итераций для верхней оценки, достаточно решить уравнение (1 = frac{n}{2^k} Rightarrow 2^i = n Rightarrow i = log_2 n). Следовательно, алгоритм имеет логарифмическую сложность: (T^{binSearch}_n = mathcal{O}(log n)).

Результаты анализа. Замечания. Литература

Оценка сложности — замечательный способ не только сравнения алгоритмов, но и прогнозирования времени их работы. Никакие тесты производительности не дадут такой информации, т.к. зависят от особенностей конкретного компьютера и обрабатывают конкретные данные (не обязательно худший случай).

Анализ алгоритмов позволяет определить минимально возможную трудоемкость, например:

• алгоритм поиска элемента в неупорядоченном массиве не может иметь верхнюю оценку сложности лучше, чем (mathcal{O}(n)). Это связано с тем, что невозможно определить отсутствие элемента в массиве (худший случай) не просмотрев все его элементы;
• возможно формально доказать, что не возможен алгоритм сортировки произвольного массива, работающий лучше чем (mathcal{O}(n cdot log n)) [5].

Нередко на собеседованиях просят разработать алгоритм с лучшей оценкой, чем возможно. Сами задачи при этом сводятся к какому-либо стандартному алгоритму. Человек, не знакомый с асимптотическим анализом начнет писать код, но требуется лишь обосновать невозможность существования такого алгоритма.

1. Васильев В. С. Алгоритм. Свойства алгоритма [Электронный ресурс] – режим доступа: https://pro-prof.com/archives/578. Дата обращения: 06.01.2014.
2. Васильев В. С. Блок-схемы алгоритмов сортировки пузырьком, выбором и вставками [Электронный ресурс] – режим доступа: https://pro-prof.com/archives/1462. Дата обращения: 06.01.2014.
3. Дж. Макконелл Анализ алгоритмов. Активный обучающий подход. — 3-е дополненное издание. М: Техносфера, 2009. -416с.
4. Миллер, Р. Последовательные и параллельные алгоритмы: Общий подход / Р. Миллер, Л. Боксер ; пер. с англ. — М. : БИНОМ. Лаборатория знаний, 2006. — 406 с.
5. Скиена С. Алгоритмы. Руководство по разработке. 2-е изд.: Пер. с англ. — СПб.: БХВ-Петербург. 2011. — 720 с.: ил.

Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.

Оценка сложности

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.

Допустим, некоторому алгоритму нужно выполнить 4n3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 4 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n3), т. е. зависит от размера входных данных кубически.

Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на f(n).

Примеры

O(n) — линейная сложность

Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.

O(log n) — логарифмическая сложность

Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.

O(n²) — квадратичная сложность

Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n2.

Бывают и другие оценки по сложности, но все они основаны на том же принципе.

Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.

Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.

Наглядно

Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10⁶ операций в секунду:

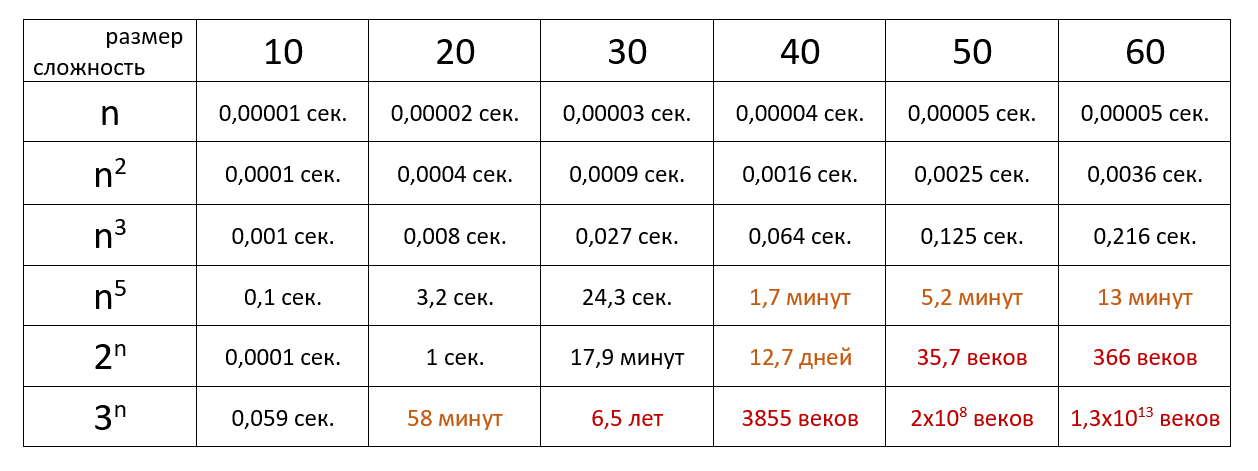Тут можно посмотреть сложность основных алгоритмов сортировки и работы с данными.

Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».

Вычисли́тельная сло́жность — понятие в информатике и теории алгоритмов, обозначающее функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных. Раздел, изучающий вычислительную сложность, называется теорией сложности вычислений. Объём работы обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения задачи, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа?». Здесь под размером входа понимается длина описания данных задачи в битах (например, в задаче коммивояжёра длина входа почти пропорциональна количеству городов и дорог между ними), а под размером выхода — длина описания решения задачи (наилучшего маршрута в задаче коммивояжёра).

В частности, теория сложности вычислений определяет NP-полные задачи, которые недетерминированная машина Тьюринга может решить за полиномиальное время, тогда как для детерминированной машины Тьюринга полиномиальный алгоритм неизвестен. Обычно это сложные задачи оптимизации, например, задача коммивояжёра.

С теоретической информатикой тесно связаны такие области как анализ алгоритмов и теория вычислимости. Связующим звеном между теоретической информатикой и алгоритмическим анализом является тот факт, что их формирование посвящено анализу необходимого количества ресурсов определённых алгоритмов решения задач, тогда как более общим вопросом является возможность использования алгоритмов для подобных задач. Конкретизируясь, попытаемся классифицировать проблемы, которые могут или не могут быть решены при помощи ограниченных ресурсов. Сильное ограничение доступных ресурсов отличает теорию вычислительной сложности от вычислительной теории, последняя отвечает на вопрос, какие задачи, в принципе, могут быть решены алгоритмически.

Временная и пространственная сложности[править | править код]

Теория сложности вычислений возникла из потребности сравнивать быстродействие алгоритмов, чётко описывать их поведение (время исполнения и объём необходимой памяти) в зависимости от размера входа.

Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.

Временная сложность алгоритма (в худшем случае) — это функция от размера входных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера.

Аналогично понятию временной сложности в худшем случае определяется понятие временная сложность алгоритма в наилучшем случае. Также рассматривают понятие среднее время работы алгоритма, то есть математическое ожидание времени работы алгоритма. Иногда говорят просто: «Временная сложность алгоритма» или «Время работы алгоритма», имея в виду временную сложность алгоритма в худшем, наилучшем или среднем случае (в зависимости от контекста).

По аналогии с временной сложностью, определяют пространственную сложность алгоритма, только здесь говорят не о количестве элементарных операций, а об объёме используемой памяти.

Асимптотическая сложность[править | править код]

Несмотря на то, что функция временной сложности алгоритма в некоторых случаях может быть определена точно, в большинстве случаев искать точное её значение бессмысленно. Дело в том, что во-первых, точное значение временной сложности зависит от определения элементарных операций (например, сложность можно измерять в количестве арифметических операций, битовых операций или операций на машине Тьюринга), а во-вторых, при увеличении размера входных данных вклад постоянных множителей и слагаемых низших порядков, фигурирующих в выражении для точного времени работы, становится крайне незначительным.

Рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма приводят к понятию асимптотической сложности алгоритма. При этом алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных, за исключением лишь, возможно, данных малого размера. Для записи асимптотической сложности алгоритмов используются асимптотические обозначения:

Обозначение	Интуитивное объяснение	Определение
	ограничена сверху функцией (с точностью до постоянного множителя) асимптотически	или
	ограничена снизу функцией (с точностью до постоянного множителя) асимптотически
	ограничена снизу и сверху функцией асимптотически
	доминирует над асимптотически
	доминирует над асимптотически
	эквивалентна асимптотически

Примеры[править | править код]

• «почистить ковёр пылесосом» требует время, линейно зависящее от его площади (), то есть на ковёр, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз объём работы увеличивается строго пропорционально в сто тысяч раз, и т. п.
• «найти имя в телефонной книге» требует всего лишь времени, логарифмически зависящего от количества записей (), так как, открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге объёмом в 1000 страниц любое имя находится не больше, чем за раз (открываний книги). При увеличении объёма страниц до ста тысяч проблема все ещё решается за заходов. (См. Двоичный поиск.)

Замечания[править | править код]

Поскольку , в асимптотической оценке сложности часто пишут «логарифм» без упоминания основания — например, .

Необходимо подчеркнуть, что степень роста наихудшего времени выполнения — не единственный или самый важный критерий оценки алгоритмов и программ. Приведем несколько соображений, позволяющих посмотреть на критерий времени выполнения с других точек зрения:

Если создаваемая программа будет использована только несколько раз, тогда стоимость написания и отладки программы будет доминировать в общей стоимости программы, то есть фактическое время выполнения не окажет существенного влияния на общую стоимость. В этом случае следует предпочесть алгоритм, наиболее простой для реализации.

Если программа будет работать только с «малыми» входными данными, то степень роста времени выполнения будет иметь меньшее значение, чем константа, присутствующая в формуле времени выполнения^[1]. Вместе с тем и понятие «малости» входных данных зависит от точного времени выполнения конкурирующих алгоритмов. Существуют алгоритмы, такие как алгоритм целочисленного умножения, асимптотически самые эффективные, но которые никогда не используют на практике даже для больших задач, так как их константы пропорциональности значительно превосходят подобные константы других, более простых и менее «эффективных» алгоритмов. Другой пример — фибоначчиевы кучи, несмотря на асимптотическую эффективность, с практической точки зрения программная сложность реализации и большие значения констант в формулах времени работы делают их менее привлекательными, чем обычные бинарные деревья^[1].

Известны случаи, когда эффективные алгоритмы требуют таких больших объёмов машинной памяти (без возможности использования внешних средств хранения), что этот фактор сводит на нет преимущество «эффективности» алгоритма. Таким образом, часто важна не только «сложность по времени», но и «сложность по памяти» (пространственная сложность).

В численных алгоритмах точность и устойчивость алгоритмов не менее важны, чем их временная эффективность.

Классы сложности[править | править код]

Класс сложности — это множество задач распознавания, для решения которых существуют алгоритмы, схожие по вычислительной сложности. Два важных представителя:

Класс P[править | править код]

Класс P вмещает все те проблемы, решение которых считается «быстрым», то есть время решения которых полиномиально зависит от размера входа. Сюда относится сортировка, поиск в массиве, выяснение связности графов и многие другие.

Класс NP[править | править код]

Класс NP содержит задачи, которые недетерминированная машина Тьюринга в состоянии решить за полиномиальное количество шагов от размера входных данных. Их решение может быть проверено детерминированной машиной Тьюринга за полиномиальное количество шагов. Следует заметить, что недетерминированная машина Тьюринга является лишь абстрактной моделью, в то время как современные компьютеры соответствуют детерминированной машине Тьюринга с ограниченной памятью. Поскольку детерминированная машина Тьюринга может рассматриваться как специальный случай недетерминированной машины Тьюринга, класс NP включает в себя класс P, а также некоторые проблемы, для решения которых известны лишь алгоритмы, экспоненциально зависящие от размера входа (то есть неэффективные для больших входов). В класс NP входят многие знаменитые проблемы, такие как задача коммивояжёра, задача выполнимости булевых формул, факторизация и др.

Проблема равенства классов P и NP[править | править код]

Вопрос о равенстве этих двух классов считается одной из самых сложных открытых проблем в области теоретической информатики. Математический институт Клэя включил эту проблему в список проблем тысячелетия, предложив награду размером в один миллион долларов США за её решение.

См. также[править | править код]

• Временная сложность алгоритма
• Класс сложности
• Алгебраическая сложность
• Скорость сходимости
• Алгоритм
• Аппроксимация
• Сведение
• «O» большое и «o» малое
• Пределы вычислений

Примечания[править | править код]

Ссылки[править | править код]

• Гирш Э. А. «Сложность вычислений и основы криптографии». Курс лекций описывающий основы сложности вычислений и криптографии.
• Юрий Лифшиц «Современные задачи теоретической информатики». Курс лекций по алгоритмам для NP-трудных задач.
• А. А. Разборов. Theoretical Computer Science: взгляд математика // Компьютерра. — 2001. — № 2. (недоступная ссылка) (альтернативная ссылка)
• А. А. Разборов. О сложности вычислений // Математическое просвещение. — МЦНМО, 1999. — № 3. — С. 127—141.

В программировании используются алгоритмы, которые по-разному решают одну и ту же задачу: например, сортировку массива. При этом алгоритмы работают с разной скоростью и требуют разное количество памяти. При прочих равных условиях мы бы выбрали быстрый или нетребовательный алгоритм.

Чтобы правильно выбирать алгоритмы, нужно научиться сравнивать их, чем мы и займемся в этом уроке. Мы познакомимся с двумя основными способами, разберем их плюсы и минусы. Опираясь на эти способы, мы сравним время работы уже знакомых нам алгоритмов.

const quickSort = (items) => {
  const partition = (items, left, right, pivot) => {
    while (true) {
      while (items[left] < pivot) {
        left++;
      }

      while (items[right] > pivot) {
        right--;
      }

      if (left >= right) {
        return right + 1;
      }

      const t = items[left];
      items[left] = items[right];
      items[right] = t;

      left++;
      right--;
    }
  };

  const quickSort = (items, left, right) => {
    const length = right - left + 1;
    if (length < 2) {
      return;
    }

    const pivot = items[left];

    const split_index = partition(items, left, right, pivot);

    quickSort(items, left, split_index - 1);
    quickSort(items, split_index, right);
  };

  quickSort(items, 0, items.length - 1);
};


const items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
const start = performance.now();
quickSort(items);
const end = performance.now();
console.log(end - start); // <= 0.20 миллисекунд

def quick_sort(items):
    def partition(items, left, right, pivot):
        while True:
            while items[left] < pivot:
                left += 1

            while items[right] > pivot:
                right -= 1

            if left >= right:
              return right + 1

            items[left], items[right] = items[right], items[left]
            left += 1
            right -= 1

    def quick_sort(items, left, right):
        length = right - left + 1

        if length < 2:
            return

        pivot = items[left]
        split_index = partition(items, left, right, pivot)
        quick_sort(items, left, split_index - 1)
        quick_sort(items, split_index, right)

    quick_sort(items, 0, len(items) - 1)

items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
start = datetime.now();
quick_sort(items);
end = datetime.now();
print(end - start); # <= 0.20 миллисекунд

<?php

function quickSort($items)
{
    $partition = function ($items, $left, $right, $pivot) {
        while (true) {
            while ($items[$left] < $pivot) {
                $left += 1;
            }

            while ($items[$right] > $pivot) {
                $right -= 1;
            }

            if ($left >= $right) {
                return $right + 1;
            }

            $t = $items[$left];
            $items[$left] = $items[$right];
            $items[$right] = $t;

            $left += 1;
            $right -= 1;
        }
    };

    $quickSort = function ($items, $left, $right) use ($partition, &$quickSort) {
        $length = $right - $left + 1;
        if ($length < 2) {
            return;
        }

        $pivot = $items[$left];

        $splitIndex = $partition($items, $left, $right, $pivot);

        $quickSort($items, $left, $splitIndex - 1);
        $quickSort($items, $splitIndex, $right);
    };

    $quickSort($items, 0, count($items) - 1);
};

// Вспомогательная функция,
// которая возвращает количество микросекунд
function microseconds() {
    $mt = explode(' ', microtime());
    [$msec, $sec] = $mt;
    return (int)$sec * 1000000 + ((int) round($msec * 1000000));
}

$items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
$start = microseconds();
quickSort($items);
$end = microseconds();
print_r($end - $start); // <= 0.20 миллисекунд

class App {
    public static int partition(int[] items, int left, int right, int pivot) {
        while (true) {
            while (items[left] < pivot) {
                left++;
            }

            while (items[right] > pivot) {
                right--;
            }

            if (left >= right) {
                return right + 1;
            }

            var temporary = items[left];
            items[left] = items[right];
            items[right] = temporary;

            left++;
            right--;
        }
    }

    public static void sort(int[] items, int left, int right) {
        var length = right - left + 1;

        if (length < 2) {
            return;
        }

        var pivot = items[left];

        var splitIndex = partition(items, left, right, pivot);
        sort(items, left, splitIndex - 1);
        sort(items, splitIndex, right);
    }

    public static void quicksort(int[] items) {
        sort(items, 0, items.length - 1);
    }
}

int[] items = {86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28};

var start = Instant.now().toEpochMilli();
App.quicksort(items);
var end = Instant.now().toEpochMilli();
System.out.println(end - start); // 0.2 миллисекунд

const selectionSort = (items) => {
  for (i = 0; i < items.length - 1; i++) {
    let indexMin = i;
    for (j = i + 1; j < items.length; j++) {
      if (items[j] < items[indexMin])
        indexMin = j;
    }

    const t = items[i];
    items[i] = items[indexMin];
    items[indexMin] = t;
  }
};

const items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
const start = performance.now();
selectionSort(items);
const end = performance.now();
console.log(end - start); // <= 0.09 миллисекунды

from datetime import datetime

def selection_sort(items):
    for i in range(len(items) - 1):
        index_min = i
        for j in range(i + 1, len(items) - 1):
              if items[j] < items[index_min]:
                  index_min = j
        items[i], items[index_min] = items[index_min], items[i]

items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28]
start = datetime.now()
selection_sort(items)
end = datetime.now()
print(end - start) # <= 0.09 миллисекунды

<?php

function selectionSort($items)
{
    for ($i = 0; $i < count($items) - 1; $i++) {
        $indexMin = $i;
        for ($j = $i + 1; $j < count($items); $j++) {
            if ($items[$j] < $items[$indexMin]) {
                $indexMin = $j;
            }
        }

        $t = $items[$i];
        $items[$i] = $items[$indexMin];
        $items[$indexMin] = $t;
    }
}

// Вспомогательная функция,
// которая возвращает количество микросекунд
function microseconds() {
    $mt = explode(' ', microtime());
    [$msec, $sec] = $mt;
    return (int)$sec * 1000000 + ((int) round($msec * 1000000));
}

$items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
$start = performance.now();
selectionSort($items);
$end = performance.now();
print_r($end - $start); // <= 0.09 миллисекунды

class App {
    public static void selectionSort(int[] items) {
        for (var i = 0; i < items.length - 1; i++) {
            var indexMin = i;
            for (var j = i + 1; j < items.length; j++) {
                if (items[j] < items[indexMin]) {
                    indexMin = j;
                }
            }

            var temporary = items[i];
            items[i] = items[indexMin];
            items[indexMin] = temporary;
        }
    }
}

int[] items = {86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28};

var start = Instant.now().toEpochMilli();
App.selectionSort(items);
var end = Instant.now().toEpochMilli();
System.out.println(end - start); // 0.09 миллисекунд

const averagePerformance = (f, count) => {
  const start = window.performance.now();

  for (let i = 0; i < count; i++) {
    f();
  }

  const end = window.performance.now();
  return (end - start) / count;
};

const items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
averagePerformance(() => selectionSort([...items]), 1); // 0.1000000238418
averagePerformance(() => selectionSort([...items]), 10); // 0.0699999988079

from datetime import datetime

def average_performance(f, count):
    start = datetime.now()

    for i in range(count):
        f()

    end = datetime.now()

    return (end - start) / count

items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28]
average_performance(selection_sort(items[:]), 1) # 0.1000000238418
average_performance(selection_sort(items[:]), 10) # 0.0699999988079

<?php

// Вспомогательная функция,
// которая возвращает количество микросекунд
function microseconds() {
    $mt = explode(' ', microtime());
    [$msec, $sec] = $mt;
    return (int)$sec * 1000000 + ((int) round($msec * 1000000));
}

function averagePerformance($f, $count)
{
    $start = microseconds();

    for ($i = 0; $i < $count; $i++) {
        $f();
    }

    $end = microseconds();
    return ($end - $start) / $count;
}

$items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28];
averagePerformance(fn() => selectionSort([...$items]), 1); // 34
averagePerformance(fn() => selectionSort([...$items]), 10); // 9.7

public class App {

    public static double averagePerformance (Runnable f, int count) {
        var start = Instant.now().toEpochMilli();

        for (var i = 0; i < count; i++) {
            f.run();
        }

        var end = Instant.now().toEpochMilli();
        System.out.println((end - start) / count);
        return (end - start) / count;
    }
}

int[] items = {86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28};

App.averagePerformance(() -> selectionSort(Arrays.copyOf(items, items.length)), 1); // 0.1
App.averagePerformance(() -> selectionSort(Arrays.copyOf(items, items.length)), 10);// 0.069

const items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28, 91, 81, 97, 24, 96, 33, 11, 47, 18, 44, 95, 34, 52, 65, 18, 5, 30, 54, 67, 24, 13, 70, 62, 88, 18, 78, 72, 40, 10, 73, 27, 44, 46, 8, 1, 49, 45, 98, 91, 70, 30, 48, 44, 52, 24, 39, 91, 22, 93, 30, 2, 85, 30, 34, 7, 82, 18, 87, 91, 37, 11, 93, 74, 27, 15, 44, 81, 15, 74, 17, 53, 3, 67, 84, 78, 98, 6, 8, 90, 50];
averagePerformance(() => selectionSort([...items]), 10); // 0.60
averagePerformance(() => quickSort([...items]), 10); // 0.19

items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28, 91, 81, 97, 24, 96, 33, 11, 47, 18, 44, 95, 34, 52, 65, 18, 5, 30, 54, 67, 24, 13, 70, 62, 88, 18, 78, 72, 40, 10, 73, 27, 44, 46, 8, 1, 49, 45, 98, 91, 70, 30, 48, 44, 52, 24, 39, 91, 22, 93, 30, 2, 85, 30, 34, 7, 82, 18, 87, 91, 37, 11, 93, 74, 27, 15, 44, 81, 15, 74, 17, 53, 3, 67, 84, 78, 98, 6, 8, 90, 50]
average_performance(selection_sort(items[:]), 10) # 0.60
average_performance(quick_sort(items[:]), 10) # 0.19

<?php

$items = [86, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28, 91, 81, 97, 24, 96, 33, 11, 47, 18, 44, 95, 34, 52, 65, 18, 5, 30, 54, 67, 24, 13, 70, 62, 88, 18, 78, 72, 40, 10, 73, 27, 44, 46, 8, 1, 49, 45, 98, 91, 70, 30, 48, 44, 52, 24, 39, 91, 22, 93, 30, 2, 85, 30, 34, 7, 82, 18, 87, 91, 37, 11, 93, 74, 27, 15, 44, 81, 15, 74, 17, 53, 3, 67, 84, 78, 98, 6, 8, 90, 50];
averagePerformance(fn() => selectionSort([...$items]), 10); // 183
averagePerformance(fn() => quickSort([...$items]), 10); // 65

int[] items = {6, 66, 44, 77, 56, 64, 76, 39, 32, 93, 33, 54, 63, 96, 5, 41, 20, 58, 55, 28, 91, 81, 97, 24, 96, 33, 11, 47, 18, 44, 95, 34, 52, 65, 18, 5, 30, 54, 67, 24, 13, 70, 62, 88, 18, 78, 72, 40, 10, 73, 27, 44, 46, 8, 1, 49, 45, 98, 91, 70, 30, 48, 44, 52, 24, 39, 91, 22, 93, 30, 2, 85, 30, 34, 7, 82, 18, 87, 91, 37, 11, 93, 74, 27, 15, 44, 81, 15, 74, 17, 53, 3, 67, 84, 78, 98, 6, 8, 90, 50};

App.averagePerformance(() -> selectionSort(Arrays.copyOf(items, items.length)), 10); // 0.6
App.averagePerformance(() -> quickSort(Arrays.copyOf(items, items.length)), 10);// 0.19

const getMinimum = (items) => {
  let minimum = items[0];

  for (let i = 1; i < items.length; i++) {
    if (minimum > items[i]) {
      minimum = items[i];
    }
  }

  return minimum;
};

def get_minimum(items):
    minimum = items[0]

    for i in range(1, len(items)):
        if minimum > items[i]:
            minimum = items[i]

    return minimum

<?php

function getMinimum($items)
{
    $minimum = $items[0];

    for ($i = 1; i < count($items); $i++) {
        if ($minimum > $items[i]) {
            $minimum = $items[i];
        }
    }

    return $minimum;
};

public class App {
    public static int getMinimum(int[] items) {
        var minimum = items[0];

        for (var i = 1; i < items.length; i++) {
            if (minimum > items[i]) {
                minimum = items[i];
            }
        }

        return minimum;
    }
}

<?php

$minimum = $items[0];

for (let i = 1; i < items.length; i++) {
  if (minimum > items[i]) {
    minimum = items[i];
  }
}

for i in range(1, len(items)):
    if minimum > items[i]:
        minimum = items[i]

<?php

for ($i = 1; $i < count($items); $i++) {
  if ($minimum > $items[$i]) {
    $minimum = $items[$i];
  }
}

for (var i = 1; i < items.length; i++) {
    if (minimum > items[i]) {
        minimum = items[i];
    }
}

const average = (items) => {
  let sum = 0;

  for (let i = 0; i < items.length; i++) {
    sum = sum + items[i];
  }

  return sum / items.length;
};

def get_average(items):
    sum = 0

    for i in range(len(items)):
        sum = sum + items[i]

    return sum / len(items)

<?php

function average($items)
{
    $sum = 0;

    for ($i = 0; $i < count($items); $i++) {
        $sum = $sum + $items[$i];
    }

    return $sum / count($items);
}

public class App {
    public static double average(int[] items) {
        double sum = 0;

        for (var i = 0; i < items.length; i++) {
            sum = sum + items[i];
        }

        return sum / items.length;
    }
}

const palindrome = (string) => {
  for (let i = 0; i < string.length / 2; i++) {
    if (string[i] != string[string.length - 1 - i]) {
      return false;
    }
  }

  return true;
};

palindrome('') // true
palindrome('a') // true
palindrome('ab') // false
palindrome('aha') // true
palindrome('abba') // true

def palindrome(string):
    for i in range(len(string) // 2):
        if string[i] != string[len(string) - 1 - i]:
            return False
    return True

palindrome('') // true
palindrome('a') // true
palindrome('ab') // false
palindrome('aha') // true
palindrome('abba') // true

<?php

function palindrome($string) => {
    for ($i = 0; $i < strlen($string) / 2; i++) {
        if ($string[$i] != $string[strlen($string) - 1 - $i]) {
            return false;
        }
    }

    return true;
}

palindrome('') // true
palindrome('a') // true
palindrome('ab') // false
palindrome('aha') // true
palindrome('abba') // true

public class App {
    public static boolean palindrome(String word) {
        for (var i = 0; i < word.length() / 2; i++) {
            if (word.charAt(i) != word.charAt(word.length() - 1 - i)) {
                return false;
            }
        }

        return true;
    }
}

App.palindrome("") // true
App.palindrome("a") // true
App.palindrome("ab") // false
App.palindrome("aha") // true
App.palindrome("abba") // true

for (i = 0; i < items.length - 1; i++) {
  for (j = i + 1; j < items.length; j++) {
    // …
  }

  // …
}

for i in range(len(items) - 1):
    for j in range(i + 1, len(items):
        # ...
    # ...

<?php

for ($i = 0; $i < count($items) - 1; $i++) {
    for ($j = $i + 1; $j < count($items); $j++) {
        // …
    }

    // …
}

for (var i = 0; i < items.length - 1; i++) {
  for (var j = i + 1; j < items.length; j++) {
    // …
  }

  // …
}

const sortedMinimum = (sortedItems) => {
  return sortedItems[0];
};

def sorted_minimum(sorted_items):
    return sorted_items[0]

<?php

function sortedMinimum($sortedItems)
{
  return $sortedItems[0];
}

public class App {
    public static int sortedMinimum(int[] sortedItems) {
        return sortedItems[0];
    }
}

const removeDuplicates = (items) => {
  const visited = new Set();
  for (let i = 0; i < items.length; i++) {
    if (visited.has(items[i])) {
      items.splice(i, 1);
      i--;
    } else {
      visited.add(items[i]);
    }
  }
};

def remove_duplicates(items):
    visited = set()
    i = 0
    while i < len(items):
        if items[i] in visited:
            items.pop(i)
            i -= 1
        else:
            visited.add(items[i])
        i += 1

<?php

function removeDuplicates($items)
{
    $visited = new DSSet();
    for ($i = 0; $i < count($items); $i++) {
        if ($visited->contains($items[$i])) {
            array_splice($items, $i, 1);
            $i--;
        } else {
            $visited->add($items[$i]);
        }
    }

    return $items;
}

public static void removeDuplicates(List<Integer> items) {
        Set<Integer> visited = new HashSet<>();

        for (var i = 0; i < items.size(); i++) {
            if(visited.contains(items.get(i))) {
                items.remove(i);
                i--;
            } else {
                visited.add(items.get(i));
            }
        }
    }

const isPrime = (n) => {
  for (let i = 2; i < n; i++) {
    if (n % i == 0) {
      return false;
    }
  }

  return true;
};

def is_prime(n):
    for i in range(2, n):
        if n % i == 0:
            return False
    return True

public class App {
    public static boolean isPrime(int n) {
        for (var i = 2; i < n; i++) {
            if (n % i == 0) {
                return false;
            }
        }

        return true;
    }
}

Сложность алгоритма – это количественная характеристика, которая говорит о том, сколько времени, либо какой объём памяти потребуется для выполнения алгоритма.

Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.

Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.

Тогда было предложено измерять сложность алгоритмов в элементарных шагах – то, сколько действий необходимо совершить для его выполнения. Любой алгоритм включает в себя определённое количество шагов и не важно на каком устройстве он будет запущен, количество шагов останется неизменным. Эту идею принято представлять в виде Big O (или О-нотации).

Big O показывает то, как сложность алгоритма растёт с увеличением входных данных. При этом она всегда показывает худший вариант развития событий – верхнюю границу.

Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.

Распространённые сложности алгоритмов

Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.

Константная – O(1).

Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.

Пример № 1.

У нас есть массив из 5 чисел и нам надо получить первый элемент.

1
2

val nums = intArrayOf(1, 2, 3, 4, 5)
val firstNumber = nums[0]

Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.

Пример № 2.

Сложение двух чисел. Функция всегда выполняет константное количество операций.

1

fun pairSum(a: Int, b: Int) = a + b

Пример № 3.

Размер массива. Опять же, функция всегда выполняет константной количество операций.

1

fun getSize(nums: List<Int>): Int = nums.size

Линейная – O(n).

Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.

Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.

Пример № 1 – Рекурсивная функция.

1
2
3
4

fun sum(n: Int): Int {
  if (n == 1) return 1
  return n + sum(n - 1)
}

Пример № 2 – Линейная функция.

1
2
3
4
5
6
7
8
9

fun pairSumSequence(n: Int): Int {
  var sum = 0
  for (i in 0 until n) {
    sum += pairSum(i, i + 1)
  }
  return sum
}

fun pairSum(a: Int, b: Int) = a + b

Функция pairSumSequence() в цикле складывает какие-либо пары чисел, вызывая функцию pairSum(). Цикл выполняется от 0 до n. Т.е. чем больше n, тем больше раз выполнится цикл. Поэтому сложность функции pairSumSequence() – O(n).

Пример № 3.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

fun sum(nums: List<Int>) {
  var sum = 0
  var product = 1

  for(num in nums) {
    sum += num
  }

  for(num in nums) {
    product *= num
  }

  println(sum, product)
}

В функции два последовательных цикла for, каждый из которых проходит массив длиной n, следовательно сложность будет: O(n + n) = O(n)

Логарифмическая – O(log n).

Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.

К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.

Линеарифметическая или линеаризованная – O(n * log n).

Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.

Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.

Квадратичная – O(n²), O(n^2).

Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.

Такие алгоритмы легко узнать по вложенным циклам.

Пример № 1.

1
2
3
4
5
6
7

fun printPairs(nums: List<Int) {
  for (i in nums) {
    for (j in nums) {
      println(nums[i], nums[j])
    }
  }
}

В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n²)

Зачем изучать Big O

• Концепцию Big O необходимо понимать, чтобы уметь видеть и исправлять неоптимальный код.
• Ни один серьёзный проект, как ни одно серьёзное собеседование, не могут обойтись без вопросов о Big O.
• Непонимание Big O ведёт к серьёзной потере производительности ваших алгоритмов.

Шпаргалка

Небольшие подсказки, которые помогут определить сложность алгоритма.

• Получение элемента коллекции это O(1). Будь то получение по индексу в массиве, или по ключу в словаре в нотации Big O это будет O(1).
• Перебор коллекции это O(n).
• Вложенные циклы по той же коллекции это O(n²).
• Разделяй и властвуй (Divide and Conquer) всегда O(log n).
• Итерации которые используют “Разделяй и властвуй” (Divide and Conquer) это O(n log n).

Полезные ссылки

Оценка сложности алгоритма. Сложность алгоритмов. Big O, Большое О – 25-минутное видео, в котором очень доступно (и с примерами) объясняются основы анализа сложности алгоритмов.
Big O – статья на хабре о Big O.
Знай сложности алгоритмов – статья рассказывает о времени выполнения и о расходе памяти большинства алгоритмов.