Теория вероятности как найти среднее значение

Теория вероятности как найти среднее значение

Как найти среднее значение распределения вероятностей (с примерами)

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

Распределение вероятностей говорит нам о вероятности того, что случайная величина примет определенные значения.

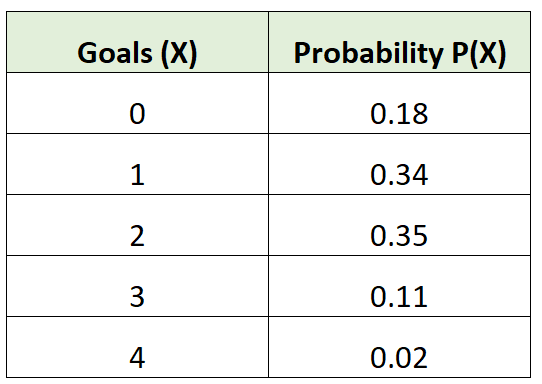
Например, следующее распределение вероятностей говорит нам о вероятности того, что определенная футбольная команда забьет определенное количество голов в данной игре:

Примечание.Вероятности в действительном распределении вероятностей всегда будут в сумме равны 1. Мы можем подтвердить, что это распределение вероятностей действительно: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.

Чтобы найти среднее (иногда называемое «ожидаемым значением») любого распределения вероятностей, мы можем использовать следующую формулу:

Mean (Or "Expected Value") of a Probability Distribution:

μ = Σx * P(x)

where:
 •x: Data value
 •P(x): Probability of value

Например, рассмотрим наше распределение вероятностей для футбольной команды:

Среднее количество голов для футбольной команды будет рассчитываться как:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гола.

В следующих примерах показано, как вычислить среднее значение распределения вероятностей в нескольких других сценариях.

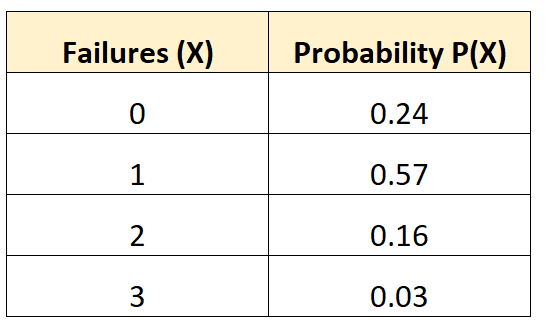
Пример 1: Среднее количество отказов транспортных средств

Следующее распределение вероятностей говорит нам о вероятности того, что данное транспортное средство испытает определенное количество отказов батареи в течение 10-летнего периода:

Пример нахождения среднего значения распределения вероятностей

Вопрос: Каково среднее количество ожидаемых отказов для этого автомобиля?

Решение.Среднее количество ожидаемых отказов рассчитывается как:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 отказов.

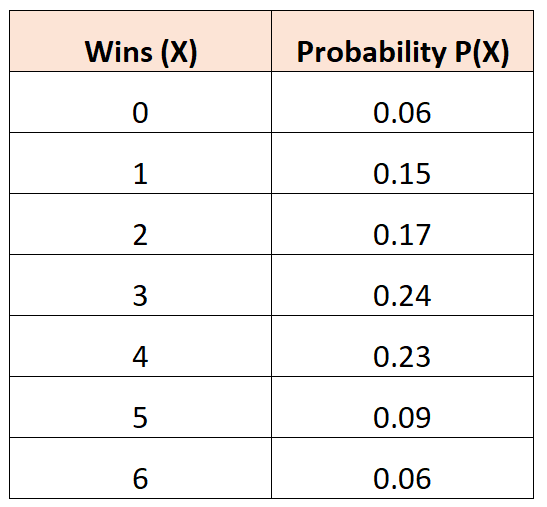
Пример 2: Среднее количество побед

Следующее распределение вероятностей говорит нам о вероятности того, что данная баскетбольная команда выиграет определенное количество игр в турнире:

Среднее значение распределения вероятностей

Вопрос: Каково среднее количество ожидаемых побед для этой команды?

Решение: Среднее количество ожидаемых выигрышей рассчитывается как:

μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 победы.

Пример 3: Среднее количество продаж

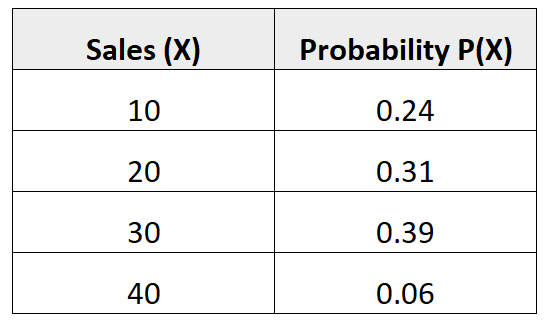
Следующее распределение вероятностей говорит нам о вероятности того, что данный продавец совершит определенное количество продаж в предстоящем месяце:

Вопрос: Каково среднее количество ожидаемых продаж этого продавца в предстоящем месяце?

Решение: Среднее количество ожидаемых продаж рассчитывается как:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 продаж.

Бонус: калькулятор распределения вероятностей

Вы можете использовать этот калькулятор для автоматического расчета среднего значения любого распределения вероятностей.

Источник

Рассмотрим ситуацию, когда случайное
явление – это числовое значение
некоторой величины. Например, число,
указанное на грани игрального кубика;
сумма выигрыша в лотерею и так далее
Пусть этих значений
и они образуют дискретный ряд
,
,
…,
.
Среди этих значений могут оказаться
одинаковые. Пусть таких групп одинаковых
значений имеется
.
Очевидно, что
.
Спрашивается, каково среднее значение
величины
?
(Например, сколько в среднем очков
выпадет при одном броске кубика?)

Будем исходить из определения среднего
значения:

. (3.11)

Однако эта же сумма может быть получена,
если провести суммирование по группам
одинаковых значений. Пусть в каждой
группе одинаковых значений по
.
Тогда:

.

Так как
– вероятность появления результата из
группы,
то получаем:

. (3.12)

Пример. Найти среднее количество
очков, выпадающее при однократном броске
игральной кости (кубика).

Так как все
,
а количество очковпринимает значения,
по формуле (3.12) получаем:

.

Величина (3.12) – это взвешенное среднеедля выборки
,
,
…,
.

5. Понятие условной вероятности

Отметим, что события
имогут бытьзависимыми– это наиболее
общий случай. Зависимость случайных
событий означает, что одно из них
оказывает влияние на другое.

Например, Вы случйно встретили знакомого
на вечеринке (событие
);
однако Ваше появление на этой вечеринке
также событие, строго говоря, случайное
(событие).
Таким образом, случайное событиеоказывается следствием случайного
события.

Заметим, что вероятность любого случайного
события зависит от каких-то условий,
при которых возможно его наступление
или ненаступление. Например, условием
того, что вероятность выпадения всех
цифр игральной кости одинакова и равна
,
является ее правильная геометрическая
форма и однородность материала. Если
условия изменятся (например, форма будет
не куб, а параллелепипед), то изменится
и вероятность.

Вероятность события
при условии, что влияющее на него событиеимело место, называетсяусловной
вероятностью.

Обозначать условную вероятность будем
.

Вероятность
событий, для которых условия не изменяются
в различных сериях опытов, называется
безусловной.

Случайные
события
инезависимы,
если их условные вероятности равны
безусловным, то есть

и. (3.13)

Перечислим некоторые
свойства условной вероятности:

  1. Если

    и    несовместны,
    то
    и;

  2. Для
    дополнительных событий
    ;

  3. Если


    и

    несовместны, то
    ,
    а также
    ;

  4. Если


    с необходимостью влечет за собой
    ,
    то есть
    ,
    то
    ;

6. Общая формула для вероятности произведения событий

Теперь при нахождении вероятности
произведения событий
рассмотрим наиболее общий случай, когда
событияимогут бытьзависимыми.

Пусть
из

равновероятных исходов опыта событие
реализуетсяспособами. Из этихисходовисходов являются благоприятными для
наступления события,
связанного с событием.
Тогда.

Пример. Имеется 3 урны, содержащие
белые и черные шары. В первой урне 2 белых
и 4 черных шара, во второй – 3 белых и 3
черных, в третьей – 4 белых и 2 черных.
Из одной из урн (неизвестно, из какой)
наугад вынут шар. Какова вероятность
того, что вынут из первой урны при
условии, что шар оказался белым?

Пусть событие
– вытаскивание белого шара, а– то, что он вынут из первой урны. Из
всех имеющихся шаров событиюблагоприятствуютшаров; из них лишьшара благоприятствуют событию.
Таким образом, получаем:.

Вероятность
совместного выполнения событий
иравна

.

Итак, окончательно
получаем:

. (3.14)

Выражение (3.14) является наиболее общим
правилом умножения вероятностей. В
частном случае независимости событий

ииз формулы (3.14) при условии (3.13) получаем
формулу (3.9).

Пример. На карточках отдельными
буквами написано слово «ПАПАХА». Карточки
переворачивают, перемешивают и случайным
образом открывают 4 из них. Какова
вероятность получить таким путем слово
«ПАПА»?

Пусть событие
– извлечение первой «П», событие– извлечение второй «А»,– третьей «П» и– четвертной «А». Тогда интересующее
нас событие можно записать как.
Его вероятность можно найти, применяя
несколько раз формулу (3.14).

;

;

;

;

;

Итак, получаем:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Макеты страниц

Тогда сумма значений случайной величины при испытаниях будет:

Чтобы найти среднее значение случайной величины т. е. значение, приходящееся на одно испытание, нужно сумму разделить на полное число испытаний:

Если мы имеем некоторую среднюю величину найденную по формуле (2.11), то, вообще говоря, при различных значениях полного числа испытаний значения средней величины также будут различными, так как рассматриваемые величины носят случайный характер. Однако при увеличении числа среднее значение данной величины будет стремиться к определенному пределу а. И чем больше будет число испытаний, тем ближе определенное по формуле (2.11), будет приближаться к этому предельному значению:

Последнее равенство представляет собой так называемый закон больших чисел или теорему Чебышева: среднее значение случайной величины будет стремиться к постоянному числу при очень большом числе измерений.

Итак, среднее значение случайной величины равна сумме произведений случайной величины на вероятность ее появления.

Если случайная величина меняется непрерывно, то ее среднее значение можно найти с помощью интегрирования:

Средние величины обладают рядом важных свойств:

1) среднее значение постоянной величины равно самой постоянной величине т. е.

2) среднее значение некоторой случайной величины есть величина постоянная, т. е.

3) среднее значение суммы нескольких случайных величин равно сумме средних значений этих величин, т. е.

4) среднее значение произведения двух взаимно независимых случайных величин равно произведению средних значений каждой из них, т. е.

Распространяя это правило на большее число независимых величин, имеем:

Иногда по тем или иным причинам знание среднего значения случайной величины оказывается недостаточным. В таких случаях ищется не просто среднее значение случайной величины, а среднее значение квадрата этой величины (квадратичное). При этом имеют место аналогичные формулы:

для дискретных значений и

в случае непрерывного изменения случайной величины.

Среднее квадратичное значение случайной величины оказывается всегда положительным и не обращается в нуль.

Часто приходится интересоваться не только средними значениями самой случайной величины, но и с редними значениями некоторых функций от случайной величины.

Например, имея распределение молекул по скоростям, мы можем найти среднюю скорость. Но также нас может интересовать средняя кинетическая энергия теплового движения, являющаяся квадратичной функцией скорости. В таких случаях можно воспользоваться следующими общими формулами, определяющими среднее значение произвольной функции случайной величины для случая дискретного распределения

для случая непрерывного распределения

Для нахождения средних значений случайной величины или функции от случайной величины с помощью ненормированной функции распределения пользуются формулами:

Здесь везде интегрирование производится по всей области возможных значений случайной величины

Отклонение от средних. В ряде случаев знание среднего и среднего квадратичного значения случайной величины оказывается недостаточным для характеристики случайной величины. Интерес представляет также распределение случайной величины около своего среднего значения. Для этого исследуется отклонение случайной величины от среднего значения.

Однако, если мы возьмем среднее отклонение случайной величины от ее среднего значения т. е. среднее значение чисел:

то получим, как в случае дискретного, так и в случае непрерывного распределения, нуль. Действительно,

и

Иногда можно находить среднее значение модулей отклонений случайной величины от среднего значения, т. е. величину:

Однако вычисления с абсолютными значениями часто сложны, а иногда и невозможны.

Поэтому гораздо чаще для характеристики распределения случайной величины около своего среднего значения используют так называемое среднее квадратичное отклонение или средний квадрат отклонения. Средний квадрат отклонения иначе называют дисперсией случайной величины. Дисперсия определяется по формулам:

которые преобразуются к одному виду (см. задачи 5, 9).

где величина представляет квадрат отклонения случайной величины от ее среднего значения.

Квадратный корень из дисперсии случайной величины называется средним квадратичным отклонением случайной величины, а для физических величин — флуктуацией:

Иногда вводится относительная флуктуация, определяемая по формуле

Таким образом, зная закон распределения случайной величины, можно определить все интересующие нас характеристики случайной величины: среднее значение, среднее квадратичное, среднее значение произвольной функции от случайной величины, средний квадрат отклонения или дисперсию и флуктуацию случайной величины.

Поэтому одной из основных задач статистической физики является отыскание законов и функций распределения тех или иных физических случайных величин и параметров в различных физических системах.

Источник

Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.

Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].

Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).

На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.

Введение[править | править код]

Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ({bar {x}}, произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.

На практике разница между μ и {bar {x}} в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда {bar {x}} (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).

Обе эти величины вычисляются одним и тем же способом:

{bar {x}}={frac {1}{n}}sum _{{i=1}}^{n}x_{i}={frac {1}{n}}(x_{1}+cdots +x_{n}).

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.

Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).

Примеры[править | править код]

  • Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
{frac {x_{1}+x_{2}+x_{3}}{3}}.
  • Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
{frac {x_{1}+x_{2}+x_{3}+x_{4}}{4}}.

Непрерывная случайная величина[править | править код]

Если существует интеграл от некоторой функции f(x) одной переменной, то среднее арифметическое этой функции на отрезке [a;b] определяется через определённый интеграл:

{displaystyle {overline {f(x)}}_{[a;b]}={frac {1}{b-a}}int _{a}^{b}f(x)dx.}

Здесь для определения отрезка [a;b] подразумевается, что {displaystyle bgeq a,} причём {displaystyle bneq a,} чтобы знаменатель не был равен 0.

Линейное преобразование[править | править код]

Линейно преобразованный набор данных {displaystyle y_{1},dots ,y_{n}} можно получить при применении линейного отображения {displaystyle y=a+bx} к метрически скалируемому набору данных x_{1},dots ,x_{n} следующим образом: {displaystyle y_{i}=a+bx_{i},iin {1,dots ,n}}. Тогда новое среднее значение набора данных будет равно {displaystyle {overline {y}}=a+b{overline {x}}}, так как {displaystyle {overline {y}}={frac {1}{n}}sum _{i=0}^{n}y_{i}={frac {1}{n}}sum _{i=0}^{n}(a+bx_{i})=a+{frac {b}{n}}sum _{i=0}^{n}bx_{i}=a+b{overline {x}}}.

Некоторые проблемы применения среднего[править | править код]

Отсутствие робастности[править | править код]

Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.

Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.

Сложный процент[править | править код]

Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.

Например, если акции в первый год упали на 10 %, а во второй год выросли на 60 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 60 %) / 2 = 25 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается 20 %.

Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 60 % — это 60 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 60 %, они в конце второго года стоят $43,2. Арифметическое среднее этого роста 25 %, но, поскольку акции выросли за 2 года всего на $13,2, средний рост в 20 % даёт конечный результат $43,2:

$30 × (1 – 0,1)*(1 + 0,6) = $30 × (1 + 0,2)*(1 + 0,2) = $43,2. Если же использовать таким же образом среднее арифметическое значение 25 %, мы не получим фактическое значение: $30 × (1 + 0,25)*(1 + 0,25) = $46,875.

Сложный процент в конце 2 года: 90 % * 160 % = 144 %, то есть общий прирост 44 %, а среднегодовой сложный процент {displaystyle {sqrt {144%}}=120%}, то есть среднегодовой прирост 20 %.

Таким образом среднегодовой прирост рассчитывается по формуле среднего геометрического

{displaystyle {sqrt {(1-0.1)(1+0.6)}}={sqrt {1.44}}=1.20 ={sqrt {(1+0.20)(1+0.20)}}}

Направления[править | править код]

При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.

Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).

Примечания[править | править код]

  1. ↑ Cantrell, David W., «Pythagorean Means» Архивная копия от 22 мая 2011 на Wayback Machine from MathWorld

См. также[править | править код]

  • Арифметическая пропорция
  • Арифметическая прогрессия
  • Неравенство Швейцера
  • Среднее арифметическое взвешенное

Ссылки[править | править код]

  • Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
  • Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
  • Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
Источник

В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями –
обновите страницу .

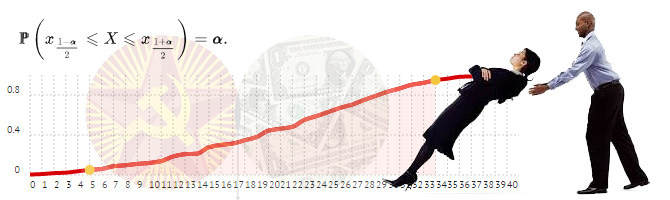
Параметры дискретного закона распределения

Параметры дискретного закона распределения

В статье описано как найти среднее значение и стандартное отклонение. Вы узнаете, что такое квантиль и каких он бывает видов, а также,
как построить доверительный интервал.

Математическое описание

Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы “на глаз” перевести
в математически обоснованное утверждение.


Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении –
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:

(2)  E(X) = Σ(pi•Xi) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:

(3)  E(X + Y) = E(X) + E(Y)
(4)  E(X•Y) = E(X) • E(Y)

Момент степени k:

(5)  νk = E(Xk)

Центральный момент степени k:

(6)  μk = E[X – E(X)]k

Среднее значение

Среднее значение (μ) закона распределения – это математическое ожидание случайной величины
(случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:

Кол-во посетителей 0 1 2 3 4 5 6
Количество наблюдений 109 21 16 68 74 16 96
Таблица 1. Количество посетителей в час

График 1. Количество посетителей в час

Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:

μ = (109 • 0 + 21 • 1 + 16 • 2 + 68 • 3 + 74 • 4 + 16 • 5 + 96 • 6) / 400 = 1209/400 = 3.02

То же самое мы можем проделать используя формулу 2:

μ = M(X) = Σ(Xi•pi) = 0 • 0.27 + 1 • 0.05 + 2 • 0.04 + 3 • 0.17 + 4 • 0.19 + 5 • 0.04 + 6 • 0.24 = 3.02 Момент первой степени, формула (5)

Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 3.02 посетителя в час

Количество посетителей 0 1 2 3 4 5 6
Вероятность (%) 27.3 5.3 4 17 18.5 4 24
Таблица 2. Закон распределения количества посетителей

Отклонение от среднего

Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:

График 2. График функции вероятности. Распределение ≈ 100±5

Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости “разность” между средним и случайными величинами:

(7) xi – μ

но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:

(8) (xi – μ)2

Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:

(9) σ2 = E[(X – E(X))2]
Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда:
(10) σ2 = E[(X – E(X))2] = ∑[(Xi – μ)2]/n
Она же формула центрального момента (6) второй степени

σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:

(11) μ±σ
(12) σ = √(σ2) = √[∑[(Xi – μ)2]/n]

Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:

σ = √(∑(x-μ)2/n) = √{[(90 – 99.95)2 + (91 – 99.95)2 + (92 – 99.95)2 + (93 – 99.95)2 + (94 – 99.95)2 + (95 – 99.95)2 + (96 – 99.95)2 + (97 – 99.95)2 + (98 – 99.95)2 + (99 – 99.95)2 + (100 – 99.95)2 + (101 – 99.95)2 + (102 – 99.95)2 + (103 – 99.95)2 + (104 – 99.95)2 + (105 – 99.95)2 + (106 – 99.95)2 + (107 – 99.95)2 + (108 – 99.95)2 + (109 – 99.95)2 + (110 – 99.95)2]/21} = 6.06

Итак, для графика 2 мы получили:

X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного “на глаз”

Квантиль

График 3. Функция распределения. Медиана

График 4. Функция распределения. 4-квантиль или квартиль

График 5. Функция распределения. 0.34-квантиль

Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.:
квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%.
На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)

  • 2-квантиль – медиана
  • 4-квантиль – квартиль
  • 10-квантиль – дециль
  • 100-квантиль – перцентиль

То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям,
и для каждого дециля нашли значение случайной величины.

Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при
p = 0.34.

Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный
квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.

Построение интервалов

Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например,
интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов:
односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.

Двусторонний доверительный интервал

Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех
событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения
случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область”

График 6. Плотность вероятности

График 7. Функция распределения с 5 и 95 перцентилями. Цветом выделен доверительный интервал с уровнем доверия 0.9

График 8. Функция вероятности и двусторонний доверительный интервал с уровнем доверия 90%

Доверительный интервал

Левосторонний и правосторонний доверительные интервалы строятся аналогично двустороннему: для левостороннего интервала мы находим перцентиль уровня
[‘один’ минус ‘уровень значимости’]. Таким образом, для построения доверительного левостороннего интервала уровня значимости 4% нам необходимо найти четвёртый перцентиль
и всё, что справа – доверительный интервал, всё что слева – критическая область.

График 9. Левосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал

График 10. Правосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал

Итого

Среднее значение – математическое ожидание случайной величины, находится по формуле:

μ = E(X) = Σ(pi•Xi)

Среднеквадратичное отклонение – математическое ожидание удалённости значений от среднего, находится по формуле:

σ = √(σ2) = √[∑[(Xi – μ)2]/n]

n-квантиль – разделение функции распределения на n равных отрезков, основные типы квантилей:

  • 2-квантиль – медиана
  • 4-квантиль – квартили
  • 10-квантиль – децили
  • 100-квантиль – перцентили

Доверительный интервал уровня α – участок функции вероятности, содержащий α всех возможных значений. Двусторонний доверительный
интервал строится отсечением (1-α)/2 справа и слева. Левосторонний и правосторонний доверительные интервалы строятся отсечением
области (1-α) слева и справа соответственно.

Построить ряд распределения

Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:

Запишем наши данные в таблицу:

89 121 128 60 126 120 119 112 85 95
105 134 85 89 100 124 109 104 119 98
69 62 103 128 114 88 133 130 60 125
128 112 68 85 83 97 105 119 95 124
81 89 111 78 81 125 66 89 97 61
78 80 110 63 101 96 69 68 122 72
77 121 109 121 131 85 64 100 120 128
70 106 125 96 83 78 62 68 79 103
116 111 103 81 75 131 110 133 96 108
113 86 60 113 93 119 106 118 126 129
Таблица 3. Вес сомалийских пиратов

Данные разобьём на группы, для начала предлагаю разбить на десять интервалов:


Узнаём максимальное и минимальное значения, вычитаем их друг из друга и делим на количество
интервалов – получили отрезки:
Максимальное значение: 134
Минимальное значение: 60
Разница: 134 – 60 = 74
Длина интервала: 74 / 10 = 7.4

Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:

# Интервал Количество элементов
1. 60 – 67.4 9
2. 67.4 – 74.8 7
3. 74.8 – 82.2 10
4. 82.2 – 89.6 12
5. 89.6 – 97 6
6. 97 – 104.4 10
7. 104.4 – 111.8 11
8. 111.8 – 119.2 11
9. 119.2 – 126.6 13
10. 126.6 – 134 10
Таблица 4. Количество элементов в интервалах

Вуа-ля, наше распределение на графике:

График 11. Ряд распределения массы тела сомалийских пиратов

Бонус

Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:

Значение интервала равно 7.4, число не является целым, поэтому
отодвигаем верхнюю границу:
Остаток от деления: [(134 – 60) / 10] = 4
Подвинуть на: 6
Новый диапазон: [60;140]

Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.

Совет

Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.

Список параметров

Итак, вот список основных параметров дискретного закона распределения:

Название Символ Формула
Математическое ожидание (среднее) E(X) Σ(pi•Xi)
Центральный момент
(среднеквадратичное отклонение)		 σx σ = √(σ2) = √[∑[(Xi – μ)2]/n]
Длина интервала R max(x) – min(x)
Мода mo max P(x = mo)
1й квантиль – F(x) = 0.25
Медиана me F(x) = 0.5
Дециль – F(x) = 0.1
Таблица 5. Основные параметры дискретного закона распределения

Шаблон гистограммы в OpenOffice Calc

Файл histogram_mock.ods содержит шаблон
построения гистограммы.

Вам понравилась статья?
/

Просмотров: 15 958

Источник

Добавить комментарий