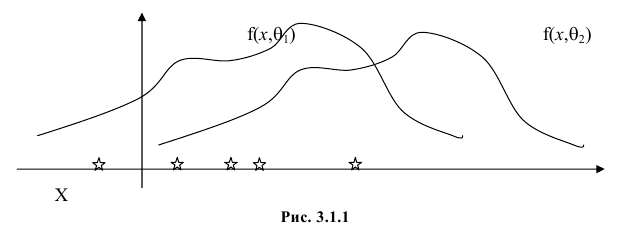
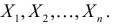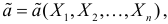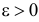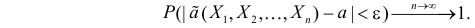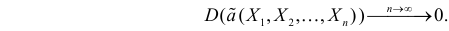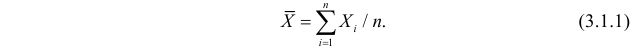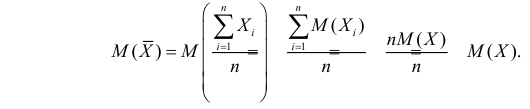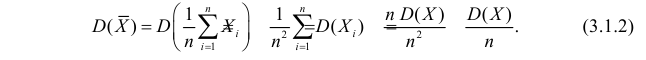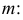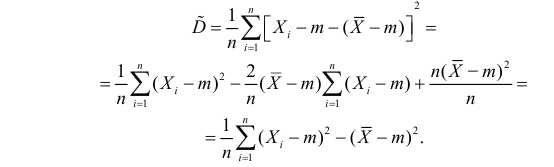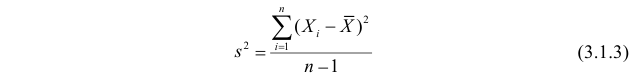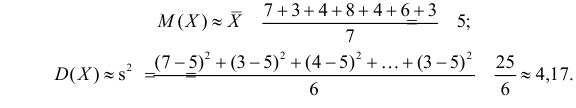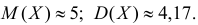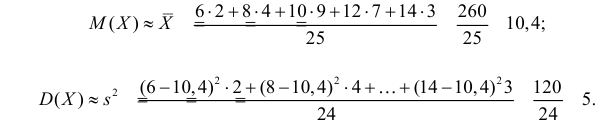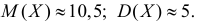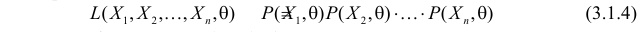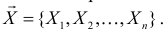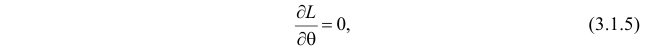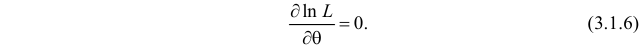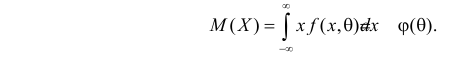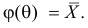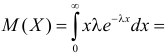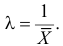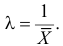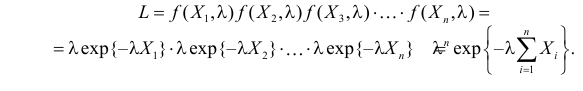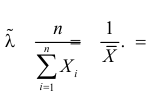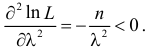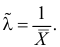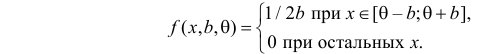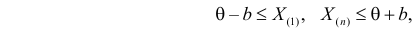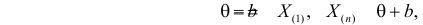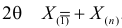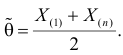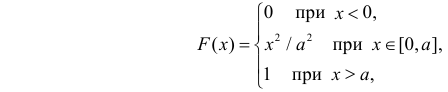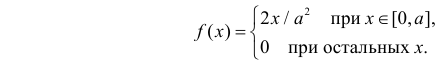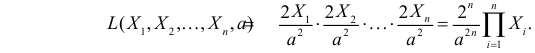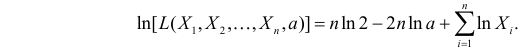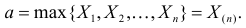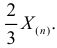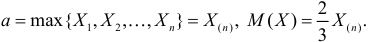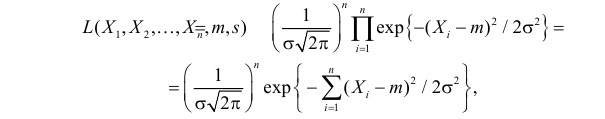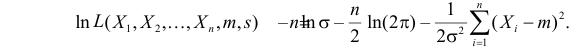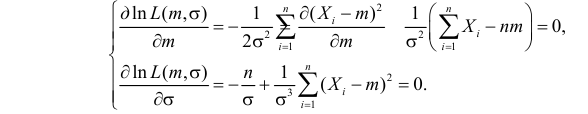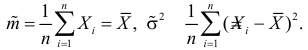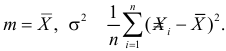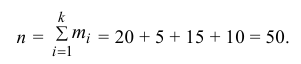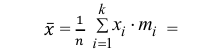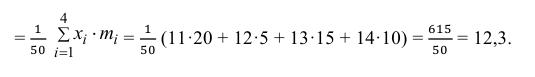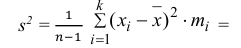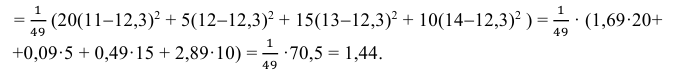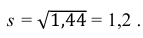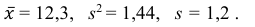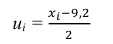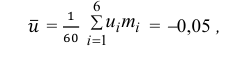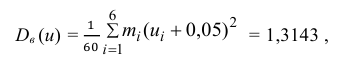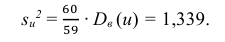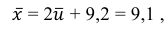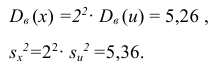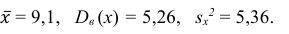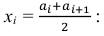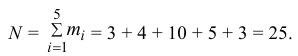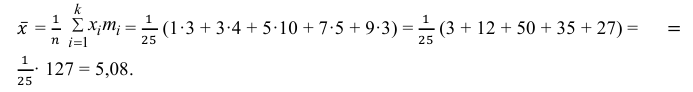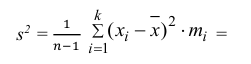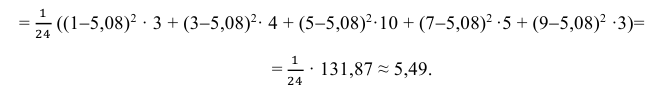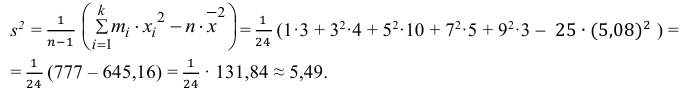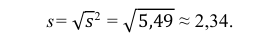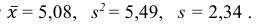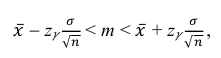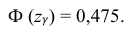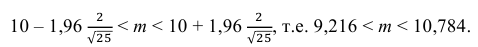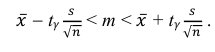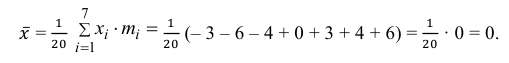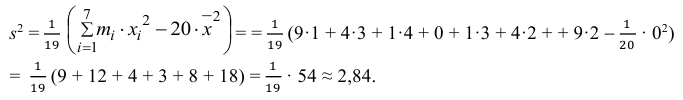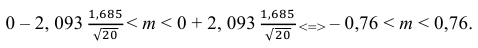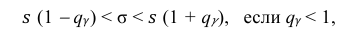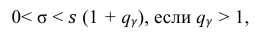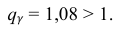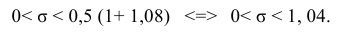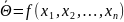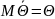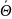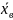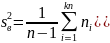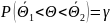Содержание:
Точечные оценки:
Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений
Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.
Определение. Функция результатов наблюдений
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 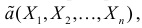
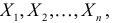
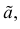
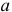
Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 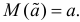
Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого
Если известно, что оценка 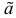
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 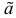
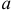
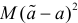
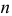
Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.
Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем 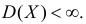
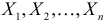
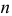
Несмещенность такой оценки следует из равенств
В силу независимости наблюдений
При условии 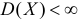
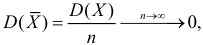
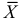
Доказано, что для математического ожидания нормально распределенной случайной величины оценка 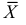
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину
Преобразуем величину 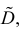
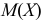
В силу (3.1.2) имеем 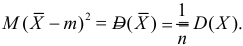
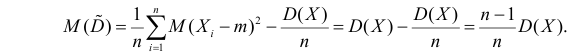
Последняя запись означает, что оценка 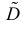
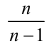
Величина
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем
Ответ.
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде:
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки:
Ответ.
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 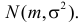
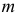
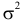
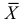
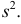
Пусть случайная величина Х имеет функцию распределения 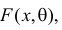
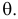
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности 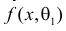
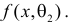
Из рисунка видно, что при значении параметра 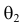
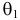
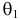
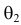
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 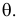
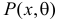
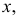
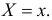
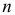
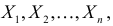
называют функцией правдоподобия. Величина 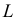
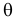
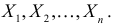
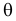


Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 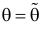

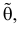
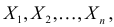
Во многих случаях, когда 
которое следует из необходимого условия экстремума. Поскольку 
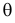

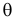
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция 


Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.
Метод моментов
Начальным моментом 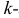
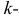
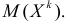
Центральным моментом 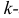
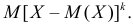
Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.
Например, если Х имеет плотность распределения 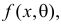
Если воспользоваться величиной 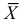
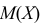
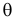
Пример:
Найти оценку параметра показательного закона распределения по методу моментов.
Решение. Плотность вероятности показательного закона распределения имеет вид 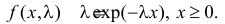
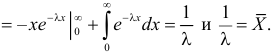
Ответ.
Пример:
Пусть имеется простейший поток событий неизвестной интенсивности 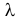
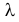
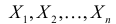

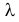
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 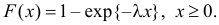
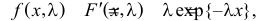
Тогда 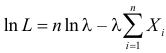
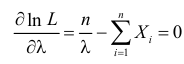
При таком значении 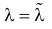
Ответ.
Определение. Пусть 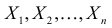
В этой записи 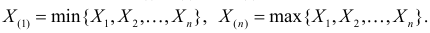
Величины 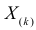
Пример:
Случайная величина Х имеет равномерное распределение на отрезке 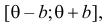


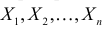


Решение. Функция плотности вероятности величины Х имеет вид
В этом случае функция правдоподобия 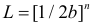




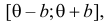
где 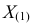
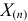

откуда 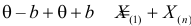
Оценкой наибольшего правдоподобия для параметра 
Ответ.
Пример:
Случайная величина X имеет функцию распределения
где 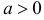
Пусть 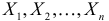

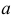
Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности
Тогда функция правдоподобия:
Логарифмическая функция правдоподобия:
Уравнение правдоподобия
не имеет решений. Критических точек нет. Наибольшее и наименьшее значения 

По виду функции 



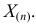
Так как 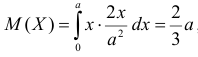
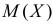
Ответ.
Пример:
Случайная величина Х имеет нормальный закон распределения 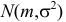
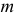
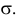
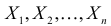
Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид
а логарифмическая функция правдоподобия:
Необходимые условия экстремума дают систему двух уравнений:
Решения этой системы имеют вид:
Отметим, что обе оценки являются состоятельными, причем оценка для 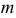
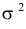
Ответ.
Пример:
По данным эксперимента построен статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:
Значит, объем выборки n = 50.
2) Вычислим среднее арифметическое значение эксперимента:
Значит, найдена оценка математического ожидания 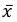
3) Вычислим исправленную выборочную дисперсию:
Значит, найдена оценка дисперсии: 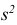
5) Вычислим оценку среднего квадратического отклонения:
Ответ:
Пример:
По данным эксперимента построен статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле
перейдем к условным вариантам:
Для них произведем расчет точечных оценок параметров:
Следовательно, вычисляем искомые точечные оценки:
Ответ:
Пример:
По данным эксперимента построен интервальный статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами
2) Объем выборки вычислим по формуле:
3) Вычислим среднее арифметическое значений эксперимента:
3) Вычислим исправленную выборочную дисперсию:
Можно было воспользоваться следующей формулой:
5) Вычислим оценку среднего квадратического отклонения:
Ответ:
Пример:
Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 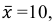
Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 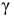
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 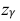
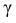
Из табл. П 2.2 приложения 2 находим: 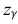
Ответ: (9,216 ; 10,784).
Пример:
По данным эксперимента построен статистический ряд:
Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; 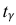
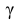
По числам 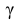
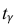
Теперь вычисляем оценки для M(X) и D(X):
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:
Ответ: (– 0,76; 0,76).
Пример:
По данным десяти независимых измерений найдена оценка квадратического отклонения 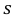
Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
Доверительный интервал для среднего квадратического отклонения находим по формуле:
где 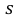
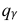
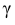
Находим:
Тогда можно записать:
Ответ: (0; 1,04).
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
-
Точечные оценки параметров распределения, их свойства
Имеется
некоторая СВ X,
значения которой мы называем генеральной
совокупностью, и которую мы на основании
выборочных значений мы должны изучить.
Если эта величина непрерывна, то она
имеет плотность распределения, если
дискретна – закон распределения. В
обоих случаях эта величина имеет функцию
распределения. Все эти функции зависят
от некоторых числовых параметров.
Точечной
оценкой параметра распределения
называется число, которое находится по
данным выборки.
.
Задача
точечной оценки состоит в том, чтобы
подобрать функцию, которая на основании
выборочных значений дала оценку
неизвестного параметра. Точечной
распределения оценкой может быть любое
число, если не уточнять какое отношение
эта оценка имеет к самому параметру.
Свойства
точечных оценок
Для
репрезентативности выборки, выборочные
значения должны быть независимыми СВ.
Значение независимых СВ, т.е значение
точечной оценки будет также случайной
величиной.
-
Точечная
оценка называется несмещенной, если
ее математическое ожидание равно
оцениваемому параметру.
-
Точечная
оценка называется эффективной, если
ее дисперсия минимальна, по сравнению
с дисперсиями других оценок, полученных
на основании выборки того же объема.
D→ min
-
Оценка
называется состоятельной, если она по
вероятности сходится к оцениваемому
параметру P(→ Θ)
→1
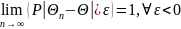
Таким
образом формулы точечных оценок
параметров распределения нужно выбирать
чтобы эта оценка обладала 3-мя свойствами,
т.е была не смещенной, эффективной и
состоятельной.
-
Точечная оценка математического ожидания, ее свойства
Точечной
оценкой математического ожидания
является выборочное среднее. Эта оценка
является несмещенной, состоятельной и
эффективной.
– выборочное
среднее.
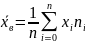
Покажем,
что эта оценка является несмещенной
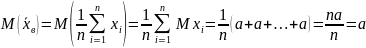
Далее
по теореме Чебышева, для любого ε>0
имеет место равенство
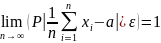
Которое
согласно условию теоремы можно переписать
так:
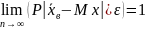
Или,
что то же самое,
,
согласно определению получаем, что
– состоятельная оценка Мx.
Также
она является и эффективной, т.е
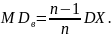
Ели
СВ непрерывная, то результаты измерений
записываются в виде интервального
вариационного ряда. И при нахождении
выборочной средней в качестве значений
xi
берут
середины интервалов.
-
Точечная оценка дисперсии, ее свойства
Для
оценки дисперсии используют выборочную
дисперсию:
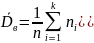
Можно
доказать, что выборочная дисперсия
является смещенной оценкой генеральной
совокупности, поэтому при небольших
объемах выборки используют исправленную
выборочную дисперсию.
Обе
этих дисперсии являются состоятельными
и эффективными оценками генеральной
дисперсии. По аналогии с дисперсией СВ
можно показать, что выборочная дисперсия
равна выборочному среднему квадратов
значений выборки минус квадрат выборочного
среднего значения:

По
исправленной выборочной дисперсии
записывают оценку среднего квадратичного
отклонения.
-
Интервальные оценки. Доверительные вероятности
Оценка
неизвестного параметра называется
интервальной, если она определяется
двумя числами – концами интервала.
Доверительным
интервалом для оценки некоторого
параметра называется интервал со
случайными концами, который с данной
вероятностью γ покрывает неизвестные
значения этого параметра.

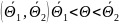
–доверительная
вероятность
Иногда
рассматривают число α = 1 – γ, которое
называют уровнем значимости. Подчеркнем,
что в формуле доверительного интервала
его концы – случайные величины.
Для
того чтобы найти доверительный интервал
для заданного параметра распределения,
необходимо знать закон распределения
точечной оценки соответствующего
параметра, поэтому доверительные
интервалы записываются для точечных
оценок конкретных законов распределения
и конкретных параметров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Реферат
на тему «Точечные оценки»
по учебной дисциплине
«ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ»
Выполнил(а):
Савкина Юлия Камильевна
2022 г
Оглавление
Введение
Статистика есть наука о том, как,
не умея мыслить и понимать,
заставить делать это цифры.
В. О. Ключевский
Математическая статистика – это наука, изучающая методы сбора и обработки статистической информации для получения научных и практических выводов.
Одной из центральных задач математической статистики является задача оценивания теоретического распределения случайной величины на основе выборочных данных. При этом часто предполагается, что вид закона распределения генеральной совокупности известен, но неизвестны параметры этого распределения, такие как математическое ожидание, дисперсия и др. Требуется найти приближенные значения этих параметров, то есть получить статистические оценки указанных параметров.
Основным методом математической статистики является выборочный метод, его суть состоит в исследовании представительной выборочной совокупности – для достоверной характеристики совокупности генеральной. Данный метод экономит временные, трудовые и материальные затраты, поскольку исследование всей совокупности зачастую затруднено или невозможно.
Для нахождения вида функции оценивания того или иного параметра используют один из следующих методов: 1) метод максимального правдоподобия; 2) метод моментов; 3) оценивание с помощью метода наименьших квадратов
Числовые характеристики, полученные по выборкам, называют статистическими оценками параметров. Различают два вида оценок параметров точечные и интервальные.
В данной работе речь пойдет именно о точечных оценках.
Глава 1. Основная часть
Основные понятия математической статистики
Введем основные понятия, связанные с выборками. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом.
Числовые характеристики всей генеральной совокупности называются параметрами. Так как всю генеральную совокупность изучить достаточно часто не представляется возможным, о параметрах судят по выборочным характеристикам. На основании выборочных данных можно получить лишь приближенное значение параметра, которое является его оценкой.
Выборочная характеристика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется точечной оценкой, т.к представляет собой число или точку на числовой оси.
Числовые характеристики выборки
По результатам выборочных наблюдений вычисляются такие статистические выборочные характеристики, как выборочные средняя, дисперсия, среднее квадратичное отклонение, коэффициент корреляции и т.д. Эти характеристики определяют соответствующие параметры генеральной совокупности.
Пусть x1, x2, …, xn – выборка из генеральной совокупности объёма n.
Выборочной средней (или средним значение выборки) называется среднее арифметическое значение признака выборочной совокупности.
Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности

Если все значения x1, x2, …, xn признака выборки объема n различны, то среднее значение выборки оценивается по формуле:

Для обозначения среднего значения выборки чаще всего используются обозначения 

Если значения признака Х1, X2, …, Хk в выборке имеют соответственно частоты n1, n2, …, nk, то последнюю формулу можно переписать в виде
Математическое ожидание характеризует среднее значение случайной величины и определяется по формулам:
|
|
(1.1) |
где mx обозначает число, полученное после вычислений по формуле (1.1); M[X] – оператор математического ожидания, ДСВ – дискретная случайная величина, НСВ – непрерывная случайная величина. Как видно из (1.1), в качестве математического ожидания используется «среднее взвешенное значение», причем каждое из значений случайной величины учитывается с «весом», пропорциональным вероятности этого значения.
Начальный момент k-го порядка случайной величины X есть математическое ожидание k-й степени этой случайной величины:
|
|
(1.2) |
При k=0 значение α0(x) = M[X0] = M [1] = 1; при k=1 — α1(x) = M[X1] = M [Х] = mx – математическое ожидание; при k=2 — α2(x) = M[X2].
Центрированной случайной величиной Х° называется случайная величина, математическое ожидание которой находится в начале координат (в центре числовой оси), т.е. M[X°] = 0. Операция центрирования (переход от нецентрированной величины Х к центрированной X°) имеет вид X° =X − mX .
Центральный момент порядка k случайной величины X есть математическое ожидание k-й степени центрированной случайной величины X:
|
|
(1.3) |
При k=0 значение 0(x)=M [X°0]=M [1]=1; при k=1 — 1(x)=M [X°1]=M [Х°] = 0; при k=2 — 2 (x)=M[X°2]= M [(X – mx)2]=M[X 2] – 2mx M [X ]+ mx2= α2 – mx2=Dx – дисперсия.
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и определяется по формулам:
|
|
(1.4) |
Дисперсия выборки или выборочная дисперсия оценивается по (слегка измененной) формуле:

Дисперсия случайной величины имеет размерность квадрата случайной величины, поэтому для анализа диапазона значений величины Х дисперсия не совсем удобна. Этого недостатка лишено среднее квадратическое отклонение (СКО), размерность которого совпадает с размерностью случайной величины. Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
|
|
(1.5) |
Мода случайной величины равна ее наиболее вероятному значению, т.е. то значение, для которого вероятность pi (для дискретной случайной величины) или f(x) (для непрерывных случайной величины) достигает максимума: f (Mo) = max, p(X = Mo) = max.
Медиана случайной величины X равна такому ее значению, для которого выполняется условие p { X < Me } = p { X Me }. Медиана, как правило, существует только для непрерывных случайных величин. Значение Me может быть определено как решение одного из следующих уравнений:
|
|
(1.6) |
В точке Me площадь, ограниченная кривой распределения делится пополам.Медиана вычисляется следующим образом. Изучаемая выборка упорядочивается в порядке возрастания (N – объем выборки). Получаемая последовательность ak, где k=1,…, N называется вариационным рядом или порядковыми статистиками.
Если число наблюдений N нечетно, то медиана оценивается как m = aN+1/2
Если число наблюдений N четно, то медиана оценивается как m = ( aN/2 + aN/2+1 ) / 2
Квантиль хp случайной величины X – это такое ее значение, для которого выполняется условие
|
p { X < xp } = F(xp)= p. (1.7) |
(1.7) |
Очевидно, что медиана – это квантиль x0,5.
Свойства точечных оценок
Статистической оценкой Qˆ неизвестного параметра Q теоретического распределения называется приближенное значение параметра, вычисленное по результатам эксперимента (по выборке). Статистические оценки делятся на точечные и интервальные. Точечной называется оценка, определяемая одним числом. Точечная оценка Qˆ параметра Q случайной величины X в общем случае равна
|
Qˆ= (x1, x2, …, xn), где xi – значения выборки. |
(1.8) |
Очевидно, что оценка Qˆ – это случайная величина, так как она является функцией от n-мерной случайной величины (Х1, …, Хn), где Хi, – значение величины Х в i-м опыте, и значения будут изменяться от выборки к выборке случайным образом. Чтобы точечная оценка была наилучшей с точки зрения точности, необходимо, чтобы она была состоятельной, несмещенной и эффективной.
Оценка Qˆ называется состоятельной, если при увеличении объема выборки n она сходится по вероятности к значению параметра Q:
|
|
(1.9) |
Состоятельность – это минимальное требование к оценкам.
Оценка Qˆ называется несмещенной, если ее математическое ожидание точно равно параметру Q для любого объема выборки:
Несмещенная оценка Qˆ является эффективной, если ее дисперсия минимальна по отношению к дисперсии любой другой оценки этого параметра:
|
|
(1.11) |
Первые два требования к оценке являются обязательными, выполнение последнего требования – желательно.
Точечная оценка математического ожидания. На основании теоремы Чебышева в качестве состоятельной оценки математического ожидания может быть использовано среднее арифметическое значений выборки 
Определим числовые характеристики оценки 

Оценка (1.12) является эффективной, т.е. ее дисперсия минимальна, если величина X распределена по нормальному закону.
Состоятельная оценка начального момента k-го порядка определяется по формуле
Точечная оценка дисперсии. В качестве состоятельной оценки дисперсии может быть использовано среднее арифметическое квадратов отклонений значений выборки от выборочного среднего:
Определим математическое ожидание оценки S2. Так как дисперсия не зависит от того, где выбрать начало координат, выберем его в точке mX, т.е. перейдем к центрированным величинам:
Ковариация Kij =0, так как опыты, а, следовательно, и Хi − значение величины Х в i‑м опыте − независимы. Таким образом, величина является смещенной оценкой дисперсии, а несмещенная состоятельная оценка дисперсии равна:
Дисперсия величины S02 равна:
Для нормального закона распределения величины X формула (1.17) примет вид
Для равномерного закона распределения –
Состоятельная несмещенная оценка среднеквадратического отклонения определяется по формуле: (1.20)
Состоятельная оценка центрального момента k-го порядка равна:
Точечная оценка вероятности. На основании теоремы Бернулли несмещенная состоятельная и эффективная оценка вероятности случайного события A в схеме независимых опытов равна частоте этого события:
где m – число опытов, в которых произошло событие A; n – число проведенных опытов. Числовые характеристики оценки вероятности p*(A) = p* равны:
Среднее арифметическое х, выборочная дисперсия Дх, частость р – это точечные статистические оценки соответственно математического ожидания (генерального среднего) МХ, дисперсии (генеральной дисперсии) ДХ, истиной (генеральной) вероятности р. Чтобы не заблудиться в этом многообразии, удобно пользоваться таблицей 1, представленной ниже [3].
Методы построения точечных оценок
Выше мы рассматривали точечные оценки основных генеральных характеристик: математического ожидания, дисперсии, вероятности и др. Однако осталось неясным, каким образом получены эти оценки. В математической статистике разработано большое число методов оценивания неизвестных параметров по данным случайной выборки, из которых наиболее часто используются:
метод моментов1;
метод максимального правдоподобия2;
метод наименьших квадратов;
графический метод (или метод номограмм).
Рассмотрим первые два из них.
Метод моментов. Пусть имеется выборка {x1, …, xn} независимых значений случайной величины с известным законом распределения f(x, Q1 , …, Qm) и m неизвестными параметрами Q1, …, Qm. Необходимо вычислить оценки Qˆ1, …, Qˆm параметров Q1, …, Qm. Последовательность вычислений следующая:
Вычислить значения m начальных и/или центральных теоретических моментов
Определить m соответствующих выборочных начальных αkˆ(x) и/или центральных µkˆ(x) моментов по формулам (1.14, 1.21).
Составить и решить относительно неизвестных параметров Q1, …, Qm систему из m уравнений, в которых теоретические моменты приравниваются к выборочным моментам. Каждое уравнение имеет вид αk(x) =αkˆ(x) или µ k(x) = µ kˆ(x). Найденные корни являются оценками Q1ˆ, …, Qmˆ неизвестных параметров.
Замечание. Часть уравнений может содержать начальные моменты, а оставшаяся часть – центральные.
Метод максимального правдоподобия. Согласно данному методу оценки Qˆ1, …, Qˆm получаются из условия максимума по параметрам Q1, …, Qm положительной функции правдоподобия L ( x1, …, xn, Q1, …, Qm). Если случайная величина X непрерывна, а значения xi независимы, то функция правдоподобия равна
Если случайная величина X дискретна и принимает независимые значения xi с вероятностями p (X=xi) = pi ( xi, Q1, …, Qm), то функция правдоподобия равна
Система уравнений согласно этому методу может записываться в двух видах:
или
Найденные корни выбранной системы уравнений являются оценками Q1ˆ, …, Qmˆ неизвестных параметров Q1, …, Qm.
Как правило оценка максимального правдоподобия эффективнее оценки, полученной методом моментов, и более того, если существует несмещенная эффективная оценка параметра, то она будет получена методом максимального правдоподобия.
Глава 2. Практическая часть
Примеры вычисления точечных оценок
Пример 1. Найдем оценку для вероятности P наступления события A по данному числу m появления этого события в n испытаниях.
Решение. Воспользуемся методом максимального правдоподобия: в этом случае функция правдоподобия L равна L = Cnm P m (1–P) n–m.
Тогда ln (L) = ln Cnm + m ln (P) + (n–m) ln (1 – P).
Уравнение для определения оценки:
Значит, оценкой методом максимального правдоподобия вероятности наступления события будет его относительная частота w.
Пример 2. Случайная величина X (число появлений события А в t независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром р. Ниже приведено эмпирическое распределение числа появлений события в 10 опытах по 5 испытаний в каждом (в первой строке указано число xi появлений события А в одном опыте; во второй строке указана частота ni — количество опытов, в которых наблюдалось столько появлений события А).
Найти методом моментов точечную оценку параметра р биномиального распределения. Оценить вероятность p0=P(X=0).
Решение. Математическое ожидание биномиального распределения известно: MX = m p. Приравняв математическое ожидание к выборочному среднему, получим уравнение: 

|
|
(05+12+21+31+41) / 10=1,1; |
||
|
|
= 1,1/5=0,22; |
|
Если распределение определяется двумя параметрами, то для построения их оценок два теоретических момента приравнивают двум соответствующим эмпирическим моментам тех же порядков (обычно первым двум).
Пример 3. Для изучения генеральной совокупности относительно некоторого количественного признака была извлечена выборка:
Найти несмещенные оценки генеральной средней и генеральной дисперсии.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя:
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия:

Пример 4. По выборке объема N=41 найдена смещенная оценка генеральной дисперсии DB=3. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»

Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности:
Пример 5. Для анализа лингвистических терминологических систем взято 7 фрагментов по 250 терминоупотреблений из русских лингвистических текстов. После подсчёта в каждом фрагменте числа употреблений слова «лицо» получен следующий вариационный ряд: 1,1,3,4,9,10,12.
1) Определите по выборке несмещённую и состоятельную оценку математического ожидания М(Х) и дисперсии D(X) случайной величины Х – «число употреблений слова «лицо» в русских лингвистических текстах.
2) Найдите несмещённую, состоятельную и эффективную оценку вероятности события А= «слово лицо использовано более 5 раз».
Решение
1) Несмещённая и состоятельная оценка М(Х) есть среднее выборочное.
Несмещённая и состоятельная оценка D(X) есть исправленная выборочная дисперсия: 
2) Несмещённой, состоятельной и эффективной оценкой вероятности события А= «слово лицо использовано более 5 раз» является частота этого события Р(А):
Пример 6. Выборка задана таблицей распределения
Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.
Решение. Cначала находим 
Затем по формулам находим две другие искомые величины:
Пример 7. Из 1500 деталей отобрано 250, распределение которых по размеру Х задано в таблице:
|
xi |
7,8-8,0 |
8,0-8,2 |
8,2-8,4 |
8,4-8,6 |
8,6-8,8 |
8,8-9,0 |
|
ni |
5 |
20 |
80 |
95 |
40 |
10 |
Найти точечные оценки для среднего и дисперсии, а также дисперсию оценки среднего при повторном и бесповторном отборах.
Решение. Вычислим по формулам (используем середины интервалов сi, число интервалов r=6, объем выборки n=250):
|
сi |
7,9 |
8,1 |
8,3 |
8,5 |
8,7 |
8,9 |
|
|
ni |
5 |
20 |
80 |
95 |
40 |
10 |
n=250 |
Вычислим дисперсию оценки среднего:
для повторной выборки:
для бесповторной выборки
Пример 8. Выборочно обследовали партию кирпича. Из 100 проб в 12 случаях кирпич оказался бракованным. Найти оценку доли бракованного кирпича и дисперсию этой оценки.
Решение. По условию задачи, число бракованных изделий m=12, объем выборки n=100, тогда оценкой доли бракованных является выборочная доля
Дисперсия этой оценки для повторной выборки равна
А среднее квадратическое отклонение этой оценки равно
Задачи подобраны таким образом, чтобы показать их разнообразную тематику и способы решений. Это и доказательство свойств точечной оценки, представление выборок разными способами и вычисление точечных оценок. Чтобы облегчить свою работу, можно воспользоваться таблицей 1 (см Приложение 1).
Заключение
Точечная оценка параметра – это оценка, которая характеризуется одним конкретным числом (например, математическим ожиданием, дисперсией, средним квадратичным отклонением и т.д.). Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их основной недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема вопрос точности становится очень важным. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Решение задач математической статистики обусловливает существенный объем вычислений. Во избежание ошибок, можно воспользоваться инженерным калькулятором или выполнить вычисления с помощью офисного пакета MS Excel, в котором есть различные статистические функции и надстройки, в том числе и возможность решить задачи по теме «Анализ данных»
Список литературы
- Гмурман, В. Е. Теория вероятностей и математическая статистика: учебник для прикладного бакалавриата / В. Е. Гмурман. — 12-е изд. — Москва: Издательство Юрайт, 2019. — 479 с. — (Бакалавр. Прикладной курс). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://biblio-online.ru/bcode/431095.
- Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие для бакалавриата и специалитета / В. Е. Гмурман. — 11-е изд., перераб. и доп. — Москва: Издательство Юрайт, 2019. — 406 с. — (Бакалавр и специалист). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://biblio-online.ru/bcode/431094.
- Малугин, В. А. Теория вероятностей и математическая статистика: учебник и практикум для вузов / В. А. Малугин. — Москва: Издательство Юрайт, 2022. — 470 с. — (Высшее образование). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/viewer/teoriya-veroyatnostey-i-matematicheskaya-statistika-493318
- Малугин, В. А. Математическая статистика: учебное пособие для бакалавриата и магистратуры / В. А. Малугин. — Москва: Издательство Юрайт, 2019. — 218 с. — (Бакалавр и магистр. Академический курс). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://biblio-online.ru/bcode/441413.
- Энатская, Н. Ю. Математическая статистика и случайные процессы: учебное пособие для вузов / Н. Ю. Энатская. — Москва: Издательство Юрайт, 2022. — 201 с. — (Высшее образование). — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/viewer/matematicheskaya-statistika-i-sluchaynye-processy-490096
Приложение 1
Таблица 1. Точечные оценки случайных величин
окончание таблицы 1
Таблица1. Точечные оценки случайных величин
1 Метод моментов был впервые предложен английским ученым, основателем математической статистики К. Пирсоном (1857-1936) в 1894 году.
2 Метод максимального правдоподобия разработал английский статистик Р. Фишер, который в 1921 г доказал, что ММ-оценки чаще всего не эффективны.
1. Оценки математического ожидания
1) Оптимальной оценкой математического ожидания является выборочное среднее
$tilde{m}=bar{X}$.
Оценка является несмещённой, состоятельной, эффективной.
2) На практике нередко возникает необходимость быстрой оценки математического ожидания. Такой оценкой
может быть
$tilde{m}=frac{{{X}_{min }}+{{X}_{max }}}{2}$.
Оценка является состоятельной и, по крайней мере, асимптотически несмещённой и асимптотически эффективной.
3) В качестве оценки математического ожидания симметричного распределения может быть
использована выборочная медиана
$tilde{m}=x_{0,5}^{*}$.
Можно показать, что при больших объёмах выборки распределение статистики $X_{0,5}^{*}$ аппроксимируется
нормальным распределением $Nleft( m,sigmasqrt{frac{pi }{2n}} right)$. Таким образом, эффективность
выборочной медианы как оценки математического ожидания равна
$e(X_{0,5}^{*})=frac{1/{{I}_{n}}(m)}{pi {{sigma }^{2}}/2n}=frac{{{sigma }^{2}}/n}{pi {{sigma }^{2}}/2n}=frac{2}{pi }approx 64 %$.
Оценка является состоятельной, несмещённой, но неэффективной.
4) Рассмотрим две выборки объёмов n1 и n2 из одной генеральной
совокупности. Пусть ${{bar{X}}_{1}}$ и ${{bar{X}}_{2}}$ – выборочные средние. Тогда
агрегированная оценка математического ожидания генеральной совокупности:
$tilde{m}=frac{{{n}_{1}}{{{bar{X}}}_{1}}+{{n}_{2}}{{{bar{X}}}_{2}}}{{{n}_{1}}+{{n}_{2}}}$
является несмещённой, состоятельной, эффективной.
2. Оценки дисперсии
1) Оптимальной оценкой дисперсии является исправленная выборочная дисперсия:
${{tilde{sigma }}^{2}}=frac{1}{n-1}sumlimits_{i=1}^{n}{{{({{X}_{i}}-bar{X})}^{2}}}$.
Оценка является несмещённой, состоятельной, эффективной.
2) Выборочная дисперсия
${{tilde{sigma }}^{2}}=frac{1}{n}sumlimits_{i=1}^{n}{{{({{X}_{i}}-bar{X})}^{2}}}$.
Оценка является асимптотически несмещённой, состоятельной, асимптотически эффективной.
3) На практике нередко возникает необходимость быстрой оценки дисперсии. Такой оценкой может быть
${{tilde{sigma }}^{2}}={{left( frac{{{X}_{max }}-{{X}_{min }}}{5} right)}^{2}}$.
Оценка является грубой, для большинства распределений смещённой и неэффективной.
4) В случае если известно математическое ожидание m генеральной совокупности, оптимальной
оценкой дисперсии является статистика:
${{tilde{sigma }}^{2}}=frac{1}{n}sumlimits_{i=1}^{n}{{{({{X}_{i}}-m)}^{2}}}$.
Оценка является несмещённой, состоятельной, эффективной.
5) Рассмотрим две выборки объёмов n1 и n2 из одной генеральной
совокупности. Пусть $S_{1}^{2}$ и $S_{2}^{2}$ – исправленные выборочные дисперсии. Тогда
агрегированная оценка дисперсии генеральной совокупности
${{tilde{sigma }}^{2}}=frac{({{n}_{1}}-1)S_{1}^{2}+({{n}_{2}}-1)S_{2}^{2}}{{{n}_{1}}+{{n}_{2}}-2}$
является несмещённой, состоятельной, эффективной.
Точечные оценки параметров распределений
Точечная оценка математического ожидания
Пусть выборка из генеральной совокупности, соответствующей случайной величине x с неизвестным математическим ожиданием Mx =q и известной дисперсией
.
Рассмотрим оценку неизвестного математического ожидания
.
Оценка несмещённая, поскольку её математическое ожидание равно Mx =q :
,
Оценка состоятельная, поскольку при n®¥, :
.
Итак, для оценки неизвестного математического ожидания случайной величины будем использовать выборочное среднее: .
Точечная оценка дисперсии
Для дисперсии случайной величины
можно предложить следующую оценку:
, где
— выборочное среднее.
Доказано, что эта оценка состоятельная, но смещенная.
В качестве состоятельной несмещенной оценки дисперсии используют величину
.
Именно несмещенностью оценки объясняется ее более частое использование в качестве оценки дисперсии.
Пример 1
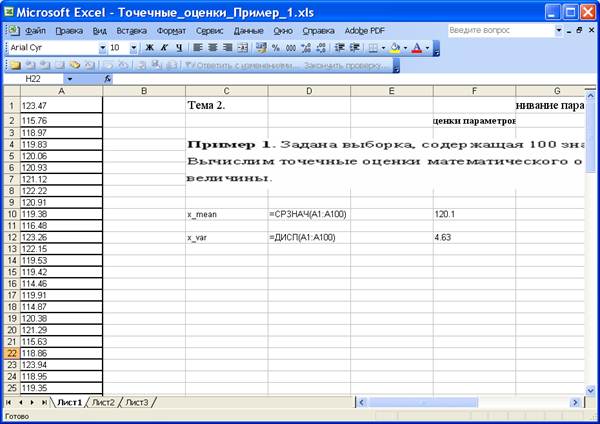
Пример 1. Задана выборка, содержащая 100 значений случайной величины.
Вычислим точечные оценки математического ожидания и дисперсии случайной величины.
На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.
Получили .
Точечная оценка вероятности события
Предположим, что в некотором эксперименте событие A происходит (благоприятный исход испытания) с вероятностью p и не происходит с вероятностью q =1– p и пусть случайная величина m — количество благоприятных исходов в серии испытаний. Задача состоит в получении по результатам серии n случайных экспериментов оценки неизвестного параметра распределения p.
При заданном числе испытаний n величина m — случайная величина, имеющая биномиальное распределение. Если событие A в серии из n независимых испытаний произошло m раз, то m — значение случайной величиныm.
Оценку величины
будем вычислять по формуле
.
Эта оценка несмещённая, состоятельная и эффективная.
Доказано, что эта оценка эффективна — обладает при прочих равных условиях минимальной дисперсией.
На рисунке приведен график зависимости точечной оценки вероятности p числа успехов от числа испытаний n в серии испытаний Бернулли. График построен по выборке 1000 значений случайной величины, имеющей биномиальное распределение с параметром p = 0.4. Видно, что с ростом числа испытаний точечная оценка приближается к известному точному значению параметра, которое равно 0.4.
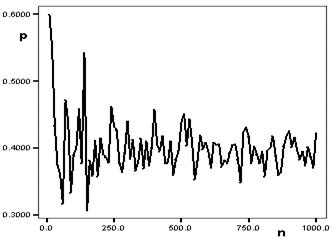
График зависимости точечной оценки вероятности от числа испытаний
Пример 2
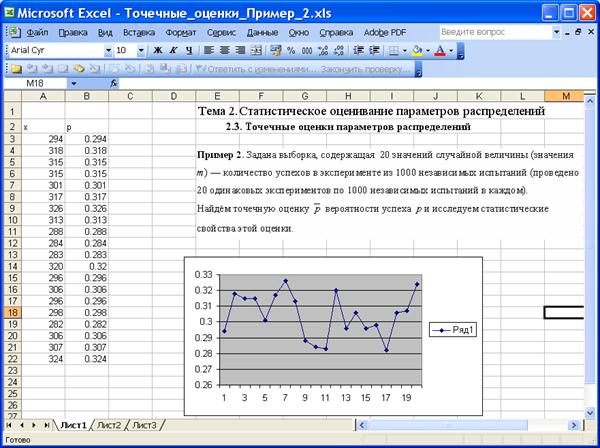
Пример 2. Задана выборка, содержащая 20 значений случайной величины (значения m) — количество успехов в эксперименте из 1000 независимых испытаний (проведено 20 одинаковых экспериментов по 1000 независимых испытаний в каждом).
Найдём точечную оценку вероятности успеха p и исследуем статистические свойства этой оценки.
На приведенных ниже рисунках изображены фрагменты листа Excel с вычислениями.
Вычисленные значения оценки вероятности записаны в столбце B. Видно, что все эти значения близки к 0.3.
Значения вероятности лежат в интервале [0.2672, 0.3525], . Можно достаточно уверенно полагать вероятность успеха равной 0.3.
Точечная оценка параметров равномерного распределения
Пусть выборка из генеральной совокупности, соответствующей случайной величине x, имеющей равномерное распределение на [0, q ] с неизвестным параметром q. Наша задача — оценить этот неизвестный параметр.
Для случайной величины x , имеющей равномерное распределение на [0, q] математическое ожидание и дисперсия известны: и
.
А поскольку оценка величины Mx известна, , то за оценку параметра q можно взять оценку
.
Несмещенность оценки очевидна: .
Состоятельность:
,
т.е. при n® ¥ дисперсия оценки стремится к нулю.
Для получения другой оценки параметра обратимся к другой статистике:
Пусть .
Найдем функцию распределения случайной величины :
, для
.
Тогда математическое ожидание и дисперсия случайной величины равны соответственно
и
, т.е. оценка
состоятельная, но смещенная.
Однако если вместо рассмотреть
, то
и
,
— состоятельная и несмещенная оценка.
А поскольку , то оценка
существенно эффективнее оценки
. Например, при
разброс оценки
в 33 раза меньше разброса оценки
.
Последний пример еще раз показывает, что выбор статистической оценки неизвестного параметра распределения — важная и нетривиальная задача.
Пример 3
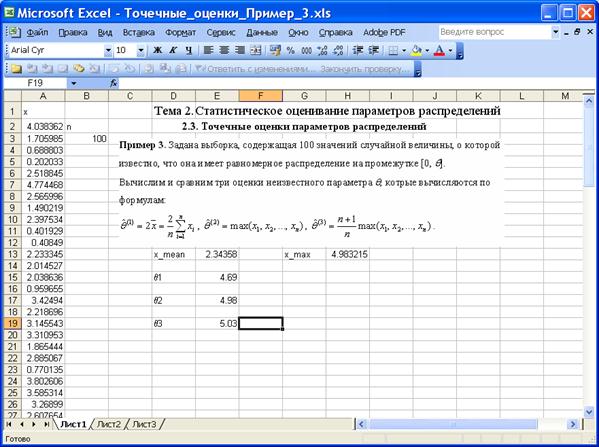
Пример 3. Задана выборка, содержащая 100 значений случайной величины, о которой известно, что она имеет равномерное распределение на промежутке [0, q].
Вычислим и сравним три оценки неизвестного параметра q, котрые вычисляются по формулам:
,
,
.
На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.
Получили, что оценки и
близки. Это и понятно, сомножитель
в оценке
при больших
мало отличается от единицы.