Точка курно как найти - Сайт, где вы сможете решить свои вопросы

Олигопольные
рынки-основа экономики индустриально
развитой страны, тк присущи отраслям
с максимальным инновационным потенциалом.
Особенности
ценообразования.
У фирм есть
возможность выбора своей ценовой
политики.
Если первая фирма
установит цену в 3 ед., то она будет ждать
от второй фирмы или установления такой
же цены (тогда их прибыль буден одинакова)
или же увеличение цены до 5 ед. (тогда
за счет покупателей второй фирмы,
ориентирующихся на более дешевый товар
первой фирмы, та увеличит объем прибыли
по сравнению с прибылью первой фирмы).
Если же первая фирма решит увеличить
цены до 5 ед., то она будет ожидать или
такого же повышения цены со стороны
второй фирмы (прибыль равна) или
уменьшения цены второй фирмы до 3 ед.
(тогда у первой фирмы прибыль будет
меньше чем у второй фирмы).
Таким образом,
фирма должна просчитать различные
реакции на свои действия со стороны
конкурента и выбрать наиболее оптимальный
и вероятный вариант. При отсутствии
сговора такой выбор достаточно сложно
сделать. Ожидая, что фирма последует
примеру и повысит цены до 5 ед., первая
фирма может оказаться в проигрыше по
прибыли и потерять долю на рынке. В
нашем случае, т.е. при отсутствии сговора,
оптимальнее устанавливать цену в 3 ед.
Если сговор есть, то можно повысить
цену до 5 ед.
Модель
курно описывает взаимодействие двух
фирм, которые принимают решения
самостоятельно, независимо и одновременно,
имеют идентичные функции спроса и
считают объемы производства другой
фирмы постоянным.
Допустим
первая фирма принмает решение о
приостановке производства (Q1=0). Тогда
рыночный спрос полностью обеспечивается
выпуском второй фирмы (Q2=D2). Если же
первая фирма начнет выпуск продукции,
то вторая будет выпускать продукцию
равную Q2=D2-Q1 , т.е. выпуск второй фирмы
будет равняться разнице между отраслевым
спросом и объемом производства первой
фирмы. При объеме производства первой
фирмы, равном всему отраслевому спросу
(Q1=D1), производство второй фирмы будет
равно нулю. В результате получится
кривая Q2(Q1) -линия реакции второй фирмы
на выпуск первой фирмы. Аналогично
строится и линия реакции первой фирмы
на объемы производства первой фирмы
Q1(Q2) . В точке пересечения этих линий
(A) наблюдается равновесие равновесие
выпуска двух фирм (Равновесие Курно):
каждая фирма правильно угадывает
поведение конкурента и принимает
оптимальные решения, при этом ни одна
из фирм не имеет стимула изменять свой
объем производства.
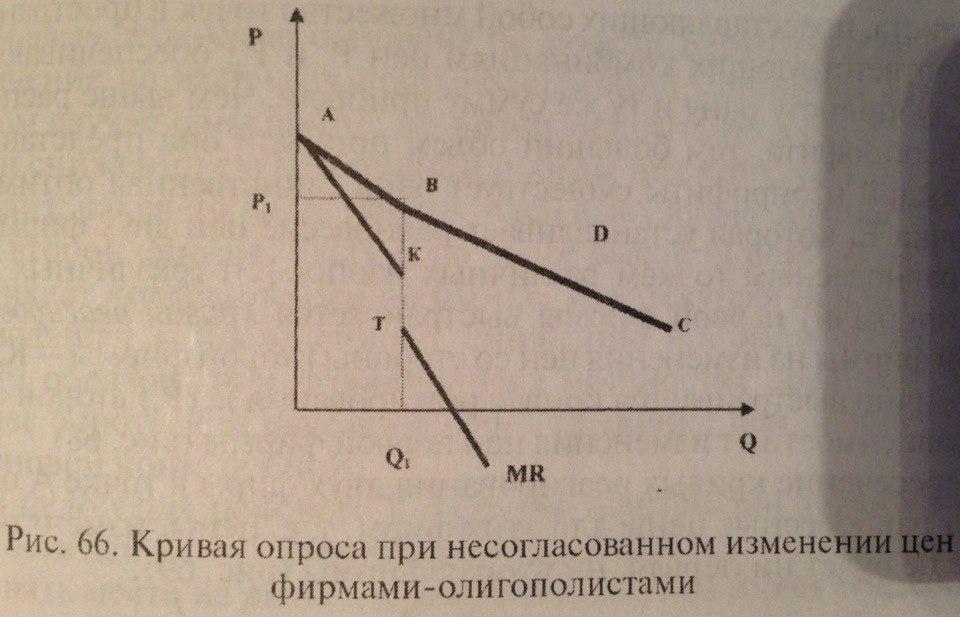
80. Ломаная кривая спроса.
Она возникает при
несогласованном изменении цен у фирм.
Если одна фирма повышает цену выше Р1,
то другие, скорее всего, этого не делают,
чтобы не потерять свою долю рынка. В
результате фирма, повысившая цену,
получает снижение спроса на свою
продукцию (Отрезок АВ ломанной кривой
спроса D) – покупатели уходят от нее к
конкурентам, сокращая объем прибыли
фирмы. При понижении цены Р1 вероятность
того, что за фирмой последуют другие
предприятия рынка отрасли, высока,
поэтому объемы продаж данной фирмы
возрастут незначительно, т.е. при
понижении цены спрос изменится меньше,
чем ожидалось (отрезок BC). В результате
фирма теряет прибыль как при повышении
цен, так и при их понижении. Кроме того,
предельный доход фирмы при ломанной
кривой спроса имеет разрыв (отрезок
КТ), не давая возможности определить
при данном объеме Q1 оптимальные цены
и издержки. Это создает условия
олигополисту для удержания цен на
прежнем уровне.
Если же возобладала
тенденция к снижению цен, то вероятно
возникновение ценовой войны, которая
ограничивается достижением равенства
цены и предельных издержек фирмы.
81. Картель как разновидность олигополии.
Олигополия —
тип
рыночной структуры несовершенной
конкуренции, в которой доминирует
крайне малое количество фирм.
Картель –
рыночная ситуация, при которой фирмы
образуют сговор относительно цен или
объема производства с целью максимизации
прибыли.
Картель.
Немногочисленность основных участников
олигополистического рынка благоприятствует
заключению между ними соглашения.
Основная идея подобного сговора состоит
в установлении объема производства и
цен на таком уровне, который обеспечивает
максимальную прибыль для всей группы,
договаривающихся компаний в целом.
Далее этот объем делится между участниками
картеля с помощью определения квоты
(доли) каждого из них в общем производстве
или путем географического закрепления
рынков (члены картеля обязуются не
вторгаться на чужие участки рынка).
Временем
расцвета картелей был период с конца
XIX и до конца 30-х гг. XX в., когда они имели
легальную форму и были широко
распространены. Если господство
одной-единственной фирмы в отрасли
представляет собой редкое и, как правило,
кратковременное явление, то картели
названного периода смогли создать
монополистическую структуру рынка в
целом ряде ведущих отраслей (электротехника,
химия, металлургия, нефтяная
промышленность), причем создать ее на
длительное время.
Особенно
сильное негативное воздействие на
экономику картели оказали в период
тяжелых кризисов перепроизводства в
30-е гг. В большинстве стран они
законодательно запрещены.
В
настоящее время картели существуют (и
преследуются властями) как тайные
сговоры. Легально они допускаются лишь
в некоторых особых сферах экономики
(например, в старых, умирающих отраслях
или в экспортной деятельности) под
контролем государства.
82. Олигополия с точки зрения теории игр.
Теория
игр ― это теория поведения субъектов
в условиях, когда решения одного из них
влияют на решения всех остальных. Она
используется для анализа действия как
отдельных людей, так и фирм. Проработанные
в экономической литературе модели
олигополии не всегда учитывают
обстоятельства образования олигопольных
рынков и влияния на них различных
изменений. Универсальным инструментом
для описаний поведения олигополии
является теория игр. Ее суть заключается
в выявлении вариантов действий, возможных
последствий последовательности
действий, а затем проведении анализа
с поиском наилучшего варианта для
каждой из сторон. Процесс такого анализа
называют игрой.
Теория
игр показывает, что: а) олигополии
являются взаимозависимыми при проведении
ценовой политики; б) сговор увеличивает
прибыль олигополии; в) олигополисты
подвержены искушению нарушить сговор.
Поведение
олигополии: взгляд с точки зрения теории
игр
Ценовое
поведение олигополии обладает
характеристиками стратегической игры
типа покера, шахмат или бриджа. Наилучший
результат игры в покер зависит от того,
что делают ваши противники. Игроки
должны строить свои действия с учетом
действий и ожидаемой реакции других
игроков.
83. Картелеподобные структуры.
Картелеподобная
структура рынка –
Компромисс между нескоординированной
олигополией и прямым сговором
представляет собой картелеподобная
структура рынка, или «игра по правилам».

Наиболее
распространенная форма олигополии на
современном этапе – картелеподобная
структура или игра по правилам. Компромисс
между нескоординированной олигополией
и прямым сговором.
Фирмы
не вступают друг с другом в соглашения,
но подчиняют свое поведение определенным
неписаным правилам. Такая политика
позволяет: избежать юр.ответственности
и уменьшить риск непредсказуемой
реакции конкурентов. “Игра по правилам”
облегчает достижение олигополистического
равновесия.
Ценновое
лидерство – крупные изменения цен
проводит одна фирма, а затем они
повторяются в близких размерах остальными
компаниями. 3 Вида ценового лидерства:
1)барометрическое лидерства(фирма 1-ая
устанавливающая цены, отслеживает
развитие в отрасли);2)лидерство на основе
низких издержек (лидер называет
оптимальные для него низкие цены с
более высокими издержками);3)лидерство
доминирующей фирмы (все фирмы принимают
цену и превращаются в ценополучателей).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

На рынке действуют две фирмы. Функция издержек для фирмы 1:

ТС(q₁) = 2 × q_1,

_{и для фирмы 2:}

ТС(q₂) = q₂²

Обратная функция рыночного спроса описывается уравнением:

P(Q) = 250 – 4 × Q,

где

Q = q₁ + q₂.

а) Определите объёмы выпуска фирм в равновесии Курно, максимизирующие их прибыли. Какой в этом случае будет рыночная цена? Какую прибыль получит каждая фирма?

б) Определите параметры рыночного равновесия по Штакельбергу. Какую прибыль получит каждая фирма?

в) Какая установится цена в соответствии с картельным соглашением?

Решение:

а) Подставим общий выпуск двух фирм

Q = q₁ + q₂

в формулу отраслевого спроса, получим:

P(Q) = 250 – 4 × (q₁ + q₂)

Распишем прибыли олигополистов:

П₁ = TR₁ – TC₁ = P × q₁– 2 × q₁= (250 – 4 × (q₁ + q₂)) × q₁ – 2 × q₁ =

= 250 × q₁ – 4 × q₁2 – 4 × q₁ × q₂ – 2 × q₁ =

=248 × q₁ – 4 × q₁² – 4 × q₁ × q₂

П₂ = TR₂ – TC₂ = P × q₂ – q₂² = (250 – 4 × (q₁ + q₂)) × q₂ – q₂² =

= 250 × q₂ – 4 × q₂² – 4 × q₁ × q₂ – q₂² =

=250 × q₂ – 5 × q₂² – 4 × q₁ × q₂

Каждая фирма стремится к максимуму прибыли.

Найдём максимум функций прибыли. Для этого приравняем к нулю первые производные полученных функций и найдём оптимальный объём выпуска:

П₁‘ = 248 – 8 × q₁ – 4 × q₂ = 0

П₂‘ = 250 – 10 × q₂ – 4 × q₁= 0

Уравнение реакции для 1 фирмы: q₁ = 31 – 0,5 × q₂

Уравнение реакции для 2 фирмы: q₂= 25 – 0,4 × q₁

Точка пересечения этих линий определяет рыночное равновесие для монополистов.

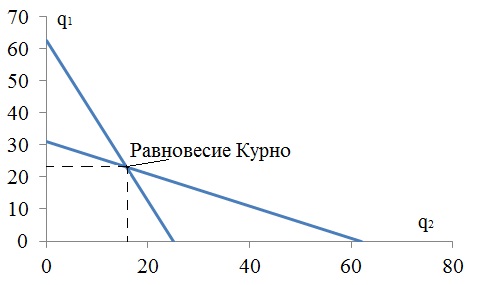
Решив систему из двух уравнений реакции дуополистов, получим равновесные значения выпуска для первой и второй фирмы.

q*₁ = 23,125

q*₂ = 15,75

Подставив равновесные значения q*₁ и q*₂ в функцию отраслевого спроса

P(Q) = 250 – 4 × (q₁ + q₂),

найдём цену равновесия.

Р = 250 – 4 × 23,125 – 4 × 15,75 = 94,5

Рассчитаем прибыль каждой фирмы в отдельности:

П₁ = 94,5 × 23,125 – 2 × 23,125 = 2139,06

П₂ = 94,5 × 15,75 – 15,75² = 1240,31

б) Пусть фирма 1 выступает в роли лидера, а фирма 2 – в роли последователя.

Тогда прибыль первой фирмы с учётом уравнения реакции фирмы 2 будет равна:

П₁ = 248 × q₁ – 4 × q₁² – 4 × q₁ × (25 – 0,4 × q₁) = 148 × q₁ – 2,4 × q₁²

Она достигает максимума при

П₁‘ = 0

148 – 4,8 × q₁ = 0

q₁ = 30,83

При этом выпуск второй фирмы станет равным:

q₂ = 25 – 0,4 × 30,83 = 12,668,

Р = 250 – 4 × 30,83 – 4 × 12,67 = 76,

П₁ = 76 × 30,83 – 2 × 30,83 = 2281,42,

П₂ = 76 × 12,67 – 12,672 = 802,39.

Таким образом, в результате пассивного поведения фирмы 2 её прибыль снизилась, а фирмы 1 возросла.

В случае лидерства фирмы 2 её прибыль будет равна:

П₂ = 250 × q₂ – 5 × q₂² – 4 × (31 – 0,5 × q₂ ) × q₂= 126 × q₂ – 3 × q₂²

Определим производную этой функции и приравняем её к нулю.

П₂‘ = 0

126 – 6 × q₂ = 0

q₂ = 21

q₁ = 31 – 0,5 × 21 = 20,5

Р = 250 – 4 × 20,5 – 4 × 21 = 84

П₁ = 84 × 20,5 – 2 × 20,5 = 1681

П₂ = 84 × 21 – 21² = 1323.

Таким образом, в результате пассивного поведения фирмы 1 её прибыль снизилась, а фирмы 2 возросла.

в) Если обе фирмы объединятся в картель, то их общая прибыль будет определяться по формуле:
Пk = TRk – TCk = (250 – 4 × q₁ – 4 × q₂) × (q₁ + q₂) – 2 × q₁ – q₂² =

= 248 × q₁ – 4 × q₁2 – 8 × q₁ × q₂+ 250 × q₂ – 5 × q₂²

Рассчитаем частные производные прибыли по аргументу q₁ и по аргументу q₂:

П_q1‘ = 248 – 8 × q₁– 8 × q₂= 0,

П_q2‘ = – 8 × q₁ + 250 – 10 × q₂ = 0.

Решим эту систему уравнений. Вычтем из второго уравнения первое и получим:

2 – 2 × q₂ = 0.

q₂ = 1,

q₁= 30,

Q = 31,

P = 250 – 4 × 31 = 126,

Прибыль картеля при этом:

Пk = (250 – 4 × 30 – 4 × 1) × 31 – 2 × 30 – 1² = 3 845

Источник

Олигополия Курно — экономическая модель рыночной конкуренции. Названа в честь сформулировавшего её французского экономиста А.Курно (1801-1877).

Основные положения модели:

На рынке действует фиксированное число фирм, выпускающих экономическое благо одного наименования;
Вход на рынок новых фирм и выход из него отсутствуют;
Фирмы обладают рыночной властью. Замечание: сам Курно не знал, что такое рыночная власть. Этот термин появился позднее;
Фирмы максимизируют свою прибыль и действуют без кооперации.

Общее количество фирм на рынке предполагается известным всем участникам. Каждая фирма, принимая своё решение, считает выпуск остальных фирм заданным параметром (константой). Функции издержек фирм $c_{i}(q_{i})$ могут быть различны и также предполагаются известными всем участникам.

Функция спроса представляет собой убывающую функцию от цены блага. Цена блага задана как цена равновесия отраслевого рынка (величина отраслевого предложения равна величине спроса на данное экономическое благо при одной и той же цене).

Вычисление равновесия[править | править код]

Рассмотрим модель с двумя фирмами (дуополию). Для определения равновесной цены вычислим наилучшие ответы каждой из фирм.

Прибыль i-й фирмы имеет вид:

$Pi _{i}=P(q_{1}+q_{2}).q_{i}-C_{i}(q_{i})$ .

Её наилучшим ответом является объём выпуска $q_{i}$ , максимизирующий прибыль $Pi _{i}$ при заданном объёме выпуска другой фирмы $q_{j},ineq j$ . Производная $Pi _{i}$ по переменной $q_{i}$ имеет вид:

${frac {partial Pi _{i}}{partial q_{i}}}={frac {partial P(q_{1}+q_{2})}{partial q_{i}}}.q_{i}+P(q_{1}+q_{2})-{frac {partial C_{i}(q_{i})}{partial q_{i}}}$

Приравнивая её к нулю, получим:

${frac {partial Pi _{i}}{partial q_{i}}}={frac {partial P(q_{1}+q_{2})}{partial q_{i}}}.q_{i}+P(q_{1}+q_{2})-{frac {partial C_{i}(q_{i})}{partial q_{i}}}=0$

Значения $q_{i}$ , удовлетворяющие данному условию, являются наилучшими ответами фирмы i. Равновесие в данной модели достигается, если $q_{1}$ является наилучшим ответом на $q_{2}$ , а $q_{2}$ – наилучшим ответом на $q_{1}$ .

Пример[править | править код]

Пусть обратная функция спроса имеет вид: $P(q_{1}+q_{2})=a-(q_{1}+q_{2})$ , а издержки $C_{i}(q_{i})$ фирмы i таковы, что ${frac {partial ^{2}C_{i}(q_{i})}{partial q_{i}^{2}}}=0$ , ${frac {partial C_{i}(q_{i})}{partial q_{j}}}=0,jneq i$ . Тогда прибыль фирмы i составит:

$Pi _{i}={bigg (}a-(q_{1}+q_{2}){bigg )}.q_{i}-C_{i}(q_{i})$

Решение задачи максимизации имеет вид:

${frac {partial {bigg (}a-(q_{1}+q_{2}){bigg )}}{partial q_{i}}}.q_{i}+a-(q_{1}+q_{2})-{frac {partial C_{i}(q_{i})}{partial q_{i}}}=0$

Таким образом, задача фирмы 1:

${frac {partial {bigg (}a-(q_{1}+q_{2}){bigg )}}{partial q_{1}}}.q_{1}+a-(q_{1}+q_{2})-{frac {partial C_{1}(q_{1})}{partial q_{1}}}=0$

$Rightarrow -q_{1}+a-(q_{1}+q_{2})-{frac {partial C_{1}(q_{1})}{partial q_{1}}}=0$

$Rightarrow q_{1}={frac {a-q_{2}-{frac {partial C_{1}(q_{1})}{partial q_{1}}}}{2}}$

Из симметрии рассматриваемой системы:

$Rightarrow q_{2}={frac {a-q_{1}-{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2}}$

Полученные выражения представляют собой функции наилучших ответов. В равновесии Нэша обе фирмы будут придерживаться стратегий, являющихся решениями пары этих уравнений. Подставляя $q_{2}$ в наилучший ответ фирмы 1, получим:

${displaystyle q_{1}={frac {a-{bigg (}{frac {a-q_{1}-{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2}}{bigg )}-{frac {partial C_{1}(q_{1})}{partial q_{1}}}}{2}}}$

${displaystyle Rightarrow q_{1}^{*}={frac {a+{frac {partial C_{2}(q_{2})}{partial q_{2}}}-2cdot {frac {partial C_{1}(q_{1})}{partial q_{1}}}}{3}}}$

${displaystyle Rightarrow q_{2}^{*}={frac {a+{frac {partial C_{1}(q_{1})}{partial q_{1}}}-2cdot {frac {partial C_{2}(q_{2})}{partial q_{2}}}}{3}}}$

Равновесием Нэша в этой системе являются объёмы выпуска ${displaystyle (q_{1}^{*},q_{2}^{*})}$ , а равновесная рыночная цена будет представлять собой величину $P(q_{1}+q_{2})=a-(q_{1}+q_{2})$ .

См. также[править | править код]

Модель Бертрана
Модель Штакельберга
Равновесие Нэша
Теория игр

Источник

Открыть эту статью в PDF

Что такое олигополия Курно

Олигополия Курно (Cournot competition) — модель поведения участников рынка, основанная на следующих предположениях:

На рынке конкурируют друг с другом несколько компаний, продающих совершенно одинаковый продукт.
Список компаний фиксированный, новые игроки не могут войти.
Компании действуют без кооперации друг с другом, то есть между ними нет ценового сговора.
У компаний есть рыночная сила, то есть решения каждой из компаний влияют на рыночную цену продукта.
Компании конкурируют, устанавливая объем производства. Цену на продукт определяет рынок с учетом общего объема предложения от всех компаний.
Каждая компания стремится максимизировать свою прибыль. При этом она предполагает, что ее решение об объеме производства не влияет на решения остальных компаний.

Пункт 5 в этом перечне — наиболее важное допущение, которое исследует модель Курно, поэтому ее часто называют «олигополия с выбором объемов производства».

Для того, чтобы модель стала понятнее, ее можно описать в менее формальном стиле:

Предположим, что на рынке действуют несколько конкурентов, продающих одинаковый продукт. Каждый может принять решение о том, сколько продукта он выпустит. Каждый знает, какое решение приняли остальные.
Цена на продукт определяется балансом спроса и предложения. У этого продукта есть кривая зависимости объемов продаж и цены. Чем больше суммарное предложение всех участников, тем ниже цена на продукт.
Участники устанавливают свой объем производства. При этом каждый, выбирая, знает, какие решения приняли остальные, и старается определить для себя такой объем, который максимизирует его прибыль. Остальные затем могут изменить свои собственные объемы, чтобы и их прибыль была максимальной с учетом изменившегося общего объема. Процесс выбора повторяется многократно до тех пор, пока на рынке не установится равновесие, при котором никто из конкурентов уже не меняет свои планы производства.

У модели Курно нет простой формулы, так как зависимость цены от объема предложения обычно представляет собой довольно сложную с точки зрения математики кривую. Но можно показать вычисления для простого условного случая.

Простой пример модели Курно

Предположим, что на рынке действуют ровно два участника. Они продают одинаковый продукт, цена на который определяется рынком и имеет очень простую формулу:

где: Q — суммарное предложение, а b — коэффициент снижения цены.

То есть, если предложение близко к нулю, то цена взлетает до Max, но с ростом предложения цена каждой единицы линейно снижается, и при некотором общем объеме продукт совершенно обесценивается.

Пусть объем производства будет от 0 до 100 единиц, то есть при предложении 100 единиц и выше цена падает до 0, и обсуждать дальнейшее производство бессмысленно.

У каждого из участников есть издержки на единицу продукта. Для начала предположим, что они одинаковые, хотя в модели можно выбрать и разные издержки.

Построим модель такого рынка. Файл Excel с моделью: cournot_model.xlsx

Если предположить, что Участник 1 постоянно выбирает объем производства первым, а Участник 2 старается подстроиться под это решение и в свою очередь выбрать наилучший вариант для себя, то мы получаем такой график зависимости прибыли Участника 1 от выбранного им объема производства:

На этом графике хорошо виден максимум прибыли, он достигается, если Участник 1 выбрал объем производства 37 единиц. Из модели мы видим, что Участник 2 при этом выберет объем 19 единиц, так как он дает ему максимальную прибыль в сложившихся условиях.

Изменение цен или затрат каждого из участников сместит равновесие на другие значения объемов производства.

Равновесие Нэша-Курно

В приведенном выше примере бросается в глаза несправедливое распределение прибыли. Участник 1 забрал себе долю рынка, которая в 2 раза больше, чем у Участника 2. При этом мы определили, что затраты на производство у них одинаковы и во всех прочих параметрах один участник не имеет никаких преимуществ над вторым.

Очевидно, что у этого рынка есть и другое равновесие, в котором доли рынка распределены наоборот: Участник 2 имеет продажи равные 37, а Участник 1 — 19. Почему Участник 2 будет мириться с таким положением вещей? Причина в том, что как только конкуренты достигают продаж 37/19, любое увеличение или уменьшение объемов для каждого из них приводит только к снижению прибыли. И соответственно, они перестают менять объемы производства, и рынок приходит в равновесие.

В нашем упрощенном примере таких точек равновесия две: 37/19 и 19/37.

То, что конкуренты могут достичь точки равновесия, из которого им сложно выйти даже если существуют и другие, более выгодные для них варианты, — важный вывод для теории олигополий и вообще для экономики. В приложении к олигополиям это равновесие называют равновесием Курно или равновесием Нэша-Курно (так как спустя более чем 100 лет идея была детальнее изучена Джоном Нэшем и стала одной из главных концепций теории игр).

История создания модели Курно и ее критика

Модель Курно была предложена французским математиком Антуаном Курно в 1838 году в книге “Recherches sur les Principes Mathématiques de la Théorie des Richesses”. Хотя она и заложила основы для математического описания поведения рынка, ее применимость к реальным рынкам в последующем критиковалась.

Одна из важных претензий к модели Курно состоит в том, что в действительности производители не устанавливают объем, под который рынок подстраивается, устанавливая цену. На практике производитель может установить цену и рассчитывать, что объем спроса соответствующим образом изменится. При таких предположениях вся модель существенно поменяется. Эта модель известна как олигополия Бертрана.

Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.

Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.

Источник

Точка Курно является термином , который особенно хорошо известен в немецкоязычных странах для точки на прайс-продаж функцией в монопольной компании , в которой компания находится на максимальной прибыли . На диаграмме количества и цены точка фиксирует две координаты количества и цены ; прибыль может быть четко определена из них. Таким образом, точка зрения Курно, грубо говоря, является ответом на вопрос, какое сочетание цены и количества является максимальной прибылью для монополиста. Это результат монопольного ценообразования .

Эта точка названа в честь французского экономиста Антуана Огюстена Курно (1801–1877).

Для точки Курно типично то, что она находится слева от максимума дохода . Другими словами: в максимуме прибыли продается меньшее количество товаров, чем было бы в случае максимума выручки.

расчет

Расчет точки Курно ( ) с максимальной ценой прибыли ( ) и максимальным объемом продаж прибыли ( ):
ПК} $x_ {c}$

В отличие от компании , находящейся в условиях совершенной конкуренции , которая должна принимать рыночную цену на свой продукт , монополист может устанавливать продажную цену таким образом, чтобы максимизировать прибыль. Для этого он должен иметь функцию спроса , т.е. ЧАС. по какой цене он может продать, сколько товара. В качестве альтернативы он может постепенно приближаться к оптимуму прибыли с помощью своей ценовой политики ( теорема о паутине ).

или, как обратная функция, функция цены-продажи как

Исходя из этого, общий доход (часто здесь продажи ) определяется как цена × количество.

При использовании функции общих затрат компания получает прибыль как
G (х)

Чтобы найти максимальную прибыль, берется первая производная от (т.е. ) и устанавливается равной нулю. Определенные нули (в случае S-образной кривой затрат или других нелинейных кривых прибыли) теперь должны быть вставлены во вторую деривацию. Нулевая точка, в которой эта вторая производная отрицательна, является максимальной доходностью , определяющей точку Курно. Чтобы получить точку Курно, соответствующая цена определяется из функции цена-продажа.
G (х) $x_ {c}$ $x_ {c}$ ПК}

Потому что, когда вы максимизируете функцию прибыли

{ Displaystyle G '(x) = U' (x) -K '(x) = 0}

даже

Можно написать, отсюда следует, что точку Курно можно также вычислить, напрямую приравняв предельные затраты к предельному доходу . Значение пересечения формирует объем прибыли максимум продаж . Это должно использоваться в функции цена-продажа, чтобы определить максимальную цену прибыли . Максимальный объем продаж с прибылью и соответствующая цена вместе образуют точку Курно.
Икс $x_ {c}$ ПК}

Числовой пример

Абсолютные значения графически: темно-синяя кривая выручки, розовая кривая затрат и зеленая кривая – итоговая прибыль, пунктирная линия показывает точку Курно.

Компания-монополист производит сверхлегкую треккинговую обувь. Управление продаж определило, что спрос [единицы] на эту обувь зависит от цены [денежные единицы (МЕ)] с функцией спроса
Икс

{ displaystyle x = x (p) = 100-0 {,} 01p}

И наоборот, функция цены-продажи (функция спроса зависит от ) дает следующий результат :
Икс

Это означает, что компания больше не продает пару по цене 10 000 GE ( запретительная цена) и не продает более 100 контейнеров даже по цене 0 GE ( количество насыщения ).

Если вы оцените запрошенное количество с соответствующей действующей ценой, вы получите оборот как функцию
Икс

${ Displaystyle U = U (x) = xp (x) = 10 000x-100x ^ {2}}$

Компания несет общие затраты на производство треккинговых ботинок, которые зависят от количества выпускаемой продукции [штук упаковки]. Затраты компании можно разбить на функцию затрат.
Икс

{ Displaystyle К = К (х) = 50 000 + 3 000 x}

подытожить. Прибыль затем рассчитывается как продажи – затраты, то есть

${ Displaystyle G = G (x) = U (x) -K (x) = 10,000x-100x ^ {2} -50,000-3,000x}$

так что одна как функция прибыли

${ displaystyle G (x) = 7,000x-100x ^ {2} -50,000}$

получает.

Чтобы получить максимум прибыли в точке Курно, определяют максимум функции прибыли путем дифференцирования :
G (х)

${ displaystyle { frac {dG} {dx}} = 7000–200x}$

Установка производной равной нулю дает решение: и .
${ displaystyle x_ {c} = 35}$ ${ displaystyle G_ {c} = 72 500}$

Поскольку вторая производная

меньше нуля, решение – максимум прибыли.

К толпе Курно

${ displaystyle x_ {c} = 35}$

принадлежит цене Курно

так

{ displaystyle p (35) = 10000–100 cdot 35}

так

${ displaystyle p_ {c} = 6500}$

Таким образом, можно продать 35 комплектов обуви по цене 6500 золотых. Это приносит компании 72 500 GE прибыли. ( )
${ Displaystyle G (35) = 7000 cdot 35-100 cdot 35 ^ {2} -50 000}$

Как объяснялось выше, также можно сделать такую же ставку. Это дает те же результаты.

Общее решение оптимизации прибыли в условиях конкуренции и с ограниченными возможностями можно найти в [Gudehus 2007]. Если необходимо сделать инвестиции для увеличения мощности, при расчете абсолютной точки Курно необходимо также принять во внимание постоянные затраты.

литература

Т. Гудехус: Динамичные рынки, практика, стратегии и преимущества для экономики и общества. Springer, Берлин / Гейдельберг / Нью-Йорк 2007, ISBN 978-3-540-72597-8 , 12.4 Максимизация прибыли . и 12,5 точка Курно.

веб ссылки

Cournotscher Punkt – статья на mikrooekonomie.de
монопольное ценообразование – определение в экономическом лексиконе Габлера

Индивидуальные доказательства

^ Артур Волль: Экономика. 12-е издание. 1996, ISBN 3-8006-2091-X , с. 205.
↑ Эдвин Бовентер, Герхард Иллинг: Введение в микроэкономику. 8. Полностью переделать. и эксп. Версия. Р. Ольденбург, 1997, ISBN 3-486-23070-0 , стр. 300.

Источник

80. Ломаная кривая спроса.

81. Картель как разновидность олигополии.

82. Олигополия с точки зрения теории игр.

83. Картелеподобные структуры.

Решение:

Вычисление равновесия[править | править код]

Пример[править | править код]

См. также[править | править код]

Что такое олигополия Курно

Простой пример модели Курно

Равновесие Нэша-Курно

История создания модели Курно и ее критика

расчет

Числовой пример

литература

веб ссылки

Индивидуальные доказательства

Вам также может понравиться

Как найти ошибки в верстке

Как найти объемную долю компонента газовой смеси

Как исправить кривошейку

Добавить комментарий Отменить ответ