Точка пересечения высот треугольника – свойства, координаты и расположение ортоцентра
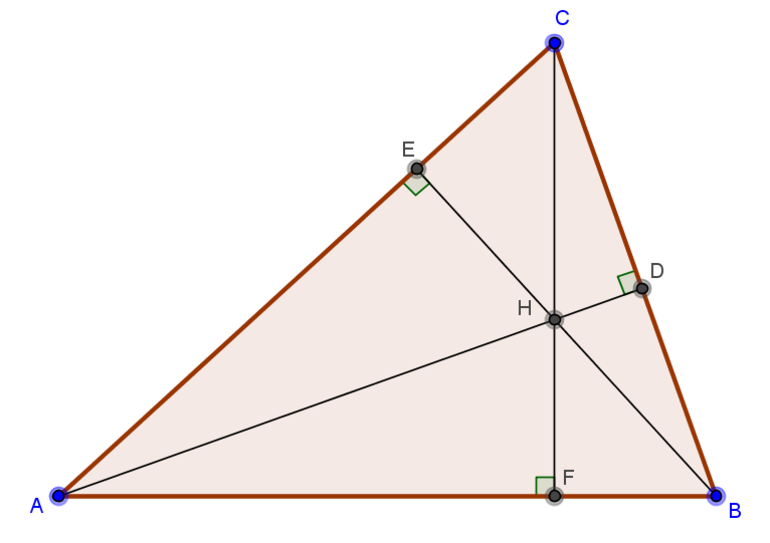
Что такое высота
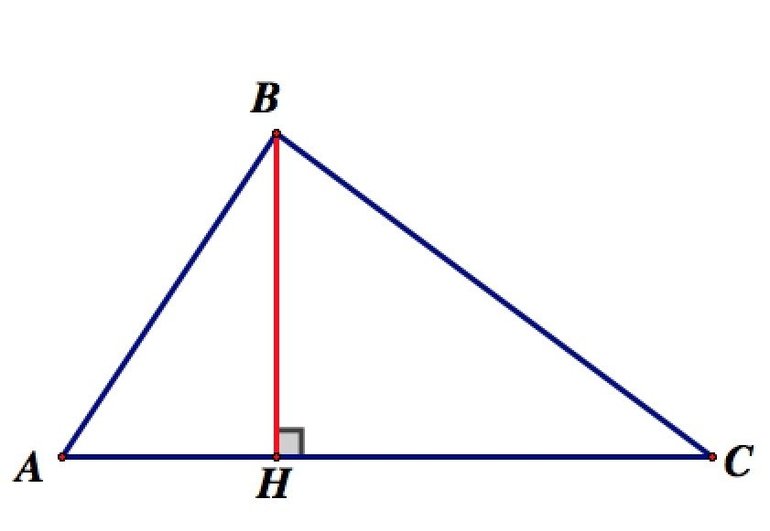
Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.
Свойства ортоцентра
Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.
Ортоцентр по отношению к фигуре может быть расположен:
- внутри;
- снаружи;
- в вершине (у прямоугольных треугольников)
Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.
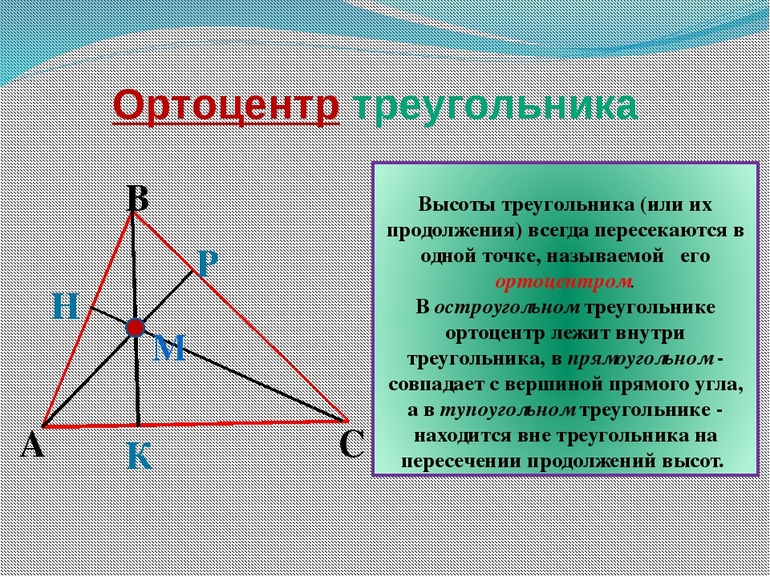
Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:
Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.
Полезные факты
Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.
Пусть:
- H — ортоцентр в ABC;
- О — центр описанной окружности.
Тогда:
- окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
- отрезок BH вдвое длиннее отрезка АС;
- середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.
Задача Фаньяно
Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.
Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.
Площадь ортотреугольника рассчитывается по формуле:
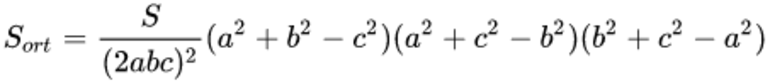
Здесь S — площадь, а, b, c — стороны.
Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.
История изучения
Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.
В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.
Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.
Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.
Ортоцентр треугольника
Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).
Пример
В приведенном ниже примере, O это ортоцентр..
Метод расчета ортоцентра треугольника
Пускай даны точки треугольника A(4,3), B(0,5) и C(3,-6).
Шаг 1
Найдем наклоны сторон AB, BC и CA используя формулу y2-y1/x2-x1. Наклон обозначим ‘m’.
- Наклон AB (m) = 5-3/0-4 = -1/2.
- Наклон BC (m) = -6-5/3-0 = -11/3.
- Наклон CA (m) = 3+6/4-3 = 9.
Шаг 2
Теперь, давайте вычислим наклон высоты AD, BE и CF который перпендикулярен сторонам BC, CA и AB соответственно. Наклон высоты = -1/наклон противоположной стороны треугольника.
- Наклон AD = -1/наклон BC = 3/11.
- Наклон BE = -1/наклон CA = -1/9.
- Наклон CF = -1/наклон AB = 2.
Шаг 3
После того, как мы нашли наклон перпендикуляров, мы должны найти уравнение линий AD, BE и CF. Давайте найдем уравнение линии AD с точкой (4,3) и наклоном 3/11.
Формула, для нахождения уравнения ортоцентра треугольника = y-y1 = m(x-x1) y-3 = 3/11(x-4)
1) Упростив выше приведенное уравнение, мы получим 3x-11y = -21
Кроме того, мы должны найти уравнение линий BE и CF. Уравнение для линии BE с точкой (0,5) и наклоном -1/9 = y-5 = -1/9(x-0)
2) Упростив выше приведенное уравнение, мы получим x + 9y = 45
Уравнение для линии CF с точкой (3,-6) и наклоном 2 = y+6 = 2(x-3)
3) Упростив выше приведенное уравнение, мы получим 2x — y = 12
Шаг 4
Найдем значение x и y решив 2 любых из 3 уравнений.
В этом примере, значение x и y (8.05263, 4.10526) которые являются координатами Ортоцентра (o).
Даны точки A(5; – 1), B(4; – 8), C(- 4; – 4). Найдите координаты точки пересечения высот треугольника ABC.
Найдём уравнение прямой BC по двум точкам:
= , или y = – x – 6.
Тогда её угловой коэффициент k1 = – . Если k2 — угловой коэффициент прямой, содержащей высоту AP, то k1 . k2 = – 1. Поэтому
k2 = – = 2.
Уравнение прямой, содержащей высоту AP треугольника ABC, найдём по точке A(5; – 1) и угловому коэффициенту k2 = 2:
Найдём уравнение прямой AC по двум точкам:
= , или y = x – .
Тогда её угловой коэффициент k3 = . Если k4 — угловой коэффициент прямой, содержащей высоту BQ, то k4 . k3 = – 1. Поэтому
k4 = – = – 3.
Уравнение прямой, содержащей высоту BQ треугольника ABC, найдём по точке B(4; – 8) и угловому коэффициенту k4 = – 3:
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений, задающих прямые AP и BQ:
Ответ
[spoiler title=”источники:”]
http://wpcalc.com/ortocentr-treugolnika/
http://gitun.com/q/18151
[/spoiler]
Как найти координаты пересечения высот в треугольнике
Линия, проведенная из вершины треугольника перпендикулярно к противоположной стороне, называется его высотой. Зная координаты вершин треугольника, можно найти его ортоцентр — точку пересечения высот.

Инструкция
Рассмотрите треугольник с вершинами A, B, C, координаты которых, соответственно (xa, ya), (xb, yb), (xc, yc). Проведите высоты из вершин треугольника и обозначьте точку пересечения высот как точку О с координатами (x, y), которые и необходимо найти.
Составьте уравнение сторон треугольника. Сторона AB выражается уравнением (x−xa)/(xb−xa)=(y−ya)/(yb−ya). Приведите уравнение к виду y=k×x+b: x×yb−x×ya−xa×yb+xa×ya=y×xb−y×xa−ya×xb+ya×xa, что равносильно y=((yb−ya)/(xb−xa))×x+xa×(ya−yb)/(xb−xa)+ya. Обозначьте угловой коэффициент k1=(yb−ya)/(xb−xa). Аналогичным образом найдите уравнение любой другой стороны треугольника. Сторона AC задается формулой (x−xc)/(xa−xc)=(y−yc)/(ya−yc), y=((ya−yc)/(xa−xc))×x+xc×(ya−yc)/(xc−xa)+ya. Угловой коэффициент k2=(yc−yb)/(xc−xb).
Запишите уранение высот треугольника, проведенных из вершин B и C. Так как высота, выходящая из вершины B, будет перпендикулярна стороне AС, то ее уравнение будет иметь вид y−ya=(-1/k2)×(x−xa). А высота, проходящая перпендикулярно стороне AB и выходящая из точки C, будет выражаться в виде y−yc=(-1/k1)×(x−xc).
Найдите точку пересечения двух высот треугольника, решив систему из двух уравнений с двумя неизвестными: y−ya=(-1/k2)×(x−xa) и y−yb=(-1/k1)×(x−xb). Выразите переменную y из обоих уравнений, приравняйте эти выражения и решите уравнение относительно x. А затем подставьте полученное значение x в одно из уравнений и найдите y.
Рассмотрите для наилучшего понимания вопроса пример. Пусть дан треугольник с вершинами A (-3, 3), B (5, -1) и C (5, 5). Составьте уравнение сторон треугольника. Сторона AB выражается по формуле (x+3)/(5+3)=(y−3)/(-1−3) или y=(-1/2)×x+3/2, то есть k1=-1/2. Сторона AC задается уравнением (x+3)/(5+3)=(y−3)/(5−3), то есть y=(1/4)×x+15/4. Угловой коэффициент k2=1/4. Уравнение высоты, выходящей из вершины C: y−5=2×(x−5) или y=2×x−5, а высоты, выходящей из вершины B: y−5=-4×(x+1), что есть y=-4×x+19. Решите систему из этих двух уравнений. Получается, что ортоцентр имеет координаты (4, 3).
Источники:
- Основные линии треугольника
- найти координаты точки на стороне треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
| Ортоцентр | |
|---|---|
 Высоты и ортоцентр |
|
| Барицентрические координаты |
 |
| Трилинейные координаты |
 |
| Код ЭЦТ | X(4) |
| Связанные точки | |
| Изогонально сопряженная | центр описанной окружности |
| Дополнительная[es] | центр описанной окружности |
| Антидополнительная[es] | точка де Лоншама[en] |
Ортоцентр (от др.-греч. ὀρθός «прямой») — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой 
Свойства[править | править код]
- Если в четвёрке точек
,
,
,
точка
является точкой пересечения высот треугольника
, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек (см. рис.).
- Более того, при любом разбиении множества ортоцентрической системы точек
на две пары, например,
и
или при любом другом подобном разбиении, всегда перпендикулярны образующиеся два отрезка прямых с концами в данных точках множеств (в нашем случае
перпендикулярно
) независимо от выбора этих двух пар
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона.
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
- Более того, при любом разбиении множества ортоцентрической системы точек

Точки, симметричные ортоцентру относительно сторон, лежат на описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности (см. рисунок)[1].
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если
— центр описанной окружности
, то
.
- При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью, всегда делится окружностью Эйлера пополам. Это следует из того, что ортоцентр есть центр гомотетии этих двух окружностей с коэффициентом
.
- Четыре попарно пересекающиеся прямые, никакие три из которых не проходят через одну точку (четырёхсторонник), при пересечении образуют четыре треугольника. Их ортоцентры лежат на одной прямой (на прямой Обера).
- Если считать, что ортоцентр треугольника делит первую высоту на части длиной
и
, вторую высоту на части длиной
и
, третью высоту на части длиной
и
, тогда
[4][5].
- Цепочка уравнений в последнем пункте:
по сути означает, что три пары отрезков, на которые ортоцентр разделяет три высоты остроугольного треугольника, подчиняются правилу хорд, пересекающихся внутри окружности, например:
. Отсюда автоматически следует то, что через четыре конца любых двух высот остроугольного треугольника всегда можно провести окружность (высоты в ней будут пересекающимися хордами). Оказывается, это утверждение сохраняет силу и для тупоугольного, и прямоугольного треугольников.
- Расстояние от стороны до центра описанной окружности равно половине расстояния от противоположной ей вершины до ортоцентра[6][7].
- Сумма квадратов расстояний от вершин до ортоцентра плюс сумма квадратов сторон равна двенадцати квадратам радиуса описанной окружности[8].
- Три основания высот остроугольного треугольника или три проекции ортоцентра на стороны треугольника образуют ортотреугольник.

Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра
- Трилинейной полярой ортоцентра является ортоцентрическая ось
(Orthic axis) (см. рис.)
- Четыре ортоцентра четырёх треугольников, образованных четырьмя попарно пересекающимися прямыми, никакие три из которых не проходят через одну точку, лежат на одной прямой (Прямая Обера четырёхугольника). Здесь используются те же четыре треугольника, что и при построении точки Микеля.
- Существует формула Карно[9]:
,
- где
,
,
— расстояния от центра описанной окружности соответственно до сторон
,
,
треугольника,
,
,
— расстояния от ортоцентра соответственно до вершин
,
,
треугольника.

В ортоцентрической системе 4 точек любая точка является ортоцентром треугольника, образованного 3 остальными точками.
- Ортоцентрическая система. Здесь O1, O2, O3 и O4 — центры окружностей четырех возможных треугольников, образованных из ортоцентрических точек A1, A2, A3 и A4 (см. рис.). Три из них вершины исходного треугольника, а четвертая — его ортоцентр. Радиусы всех четырех окружностей равны. Центры трех из четырех окружностей (кроме описанной исходного треугольника) образуют вершины треугольника, равного исходному, со сторонами, попарно параллельными сторонам исходного треугольника.
Ортоцентрическая система. Здесь O1, O2, O3 и O4 — центры окружностей четырех возможных треугольников, образованных из ортоцентрических точек A1, A2, A3 и A4.
- *Если прямая ℓ ортополюса P проходит через ортоцентр Q треугольника, то точка, расположенная на продолжении отрезка PQ, соединяющего ортополюс с ортоцентром, по другую сторону на расстоянии, равном PQ, лежит на окружности Эйлера этого треугольника.[10]
История[править | править код]
Утверждение: «Все 3 высоты треугольника пересекаются в одной точке», называемой теперь ортоцентром, в «Началах» Евклида отсутствует. Ортоцентр впервые в греческой математике использован в «Книге лемм» Архимеда, хотя явного доказательства существования ортоцентра Архимед не привёл.
Часть историков приписывает это утверждение Архимеду и называют его теоремой Архимеда[11]. До середины девятнадцатого века, ортоцентр нередко называли архимедовой точкой[12].
В явном виде это утверждение («Все 3 высоты треугольника пересекаются в одной точке») встречается у Прокла (410—485) — комментатора Евклида[13].
Другие историки математики считают автором первого доказательства Уильяма Чеппла (англ.) (рус. (Miscellanea Curiosa Mathematica, 1749 год)[14].
Термин ортоцентр впервые был использован У. Х. Безантом (англ.) (рус. в работе «Конические сечения, исследованные геометрически (1869)» ([15])[16].
См. также[править | править код]
- Высота треугольника
- Высота (геометрия)
- Замечательные точки треугольника
- Центр вписанной окружности
- Ортотреугольник
- Ортоцентроидная окружность
- Центроид
Примечания[править | править код]
- ↑ Honsberger, 1995, p. 18.
- ↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers»,
Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html Архивная копия от 28 апреля 2021 на Wayback Machine - ↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
- ↑ Altshiller-Court, 2007, p. 94.
- ↑ Honsberger, 1995, p. 20.
- ↑ Altshiller-Court, 2007, p. 99.
- ↑ Honsberger, 1995, p. 17, 23.
- ↑ Altshiller-Court, 2007, p. 102.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд. — М.: Учпедгиз, 1962. — С. 120—125 (задача), параграф 57, с. 73.
- ↑ College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. Nathan Altshiller-Court. (Параграф: G. The Orthopole. Пункт. 699. Теорема. Fig. 156. С.290-291). Mineola, New York: Dover Publication, Inc., 2012. 292 p.
- ↑ Ефремов Д. Новая геометрия треугольника. Одесса, 1902. С. 9, п. 16. Высоты треугольника. Теорема Архимеда.
- ↑ Maureen T. Carroll, Elyn Rykken. Geometry: The Line and the Circle. Дата обращения: 10 апреля 2020.
- ↑ Nathan Altshiller-Court. «College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle». Second Edition. Mineola, New York: Dover Publications, Inc. 2007. P. 298, § 175.
- ↑ Bogomolny, Alexander, A Possibly First Proof of the Concurrence of Altitudes, <https://www.cut-the-knot.org/triangle/Chapple.shtml>. Проверено 17 ноября 2019. Архивная копия от 7 мая 2021 на Wayback Machine
- ↑ Conic Sections Treated Geometrically, 1869. Ссылка: 1895: Conic sections treated geometrically Архивная копия от 18 апреля 2018 на Wayback Machine from Cornell University Historical Math Monographs.
- ↑ Nathan Altshiller-Court. «College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle». Second Edition. Mineola, New York: Dover Publications, Inc. 2007. § 176, p. 94; § 176, p. 298
Литература[править | править код]
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 37—39. — ISBN 5-94057-170-0.
- Nathan Altshiller-Court. College geometry : an introduction to the modern geometry of the triangle and the circle. — Dover Publications, Inc., 2007. — ISBN 0-486-45805-9.
- Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Mathematical Association of America, 1995. — Vol. 37. — P. 17—26. — (New Mathematical Library). — ISBN 0-88385-639-5 (Vol. 37). — ISBN 0-88385-600-X (complete set).
Ссылки[править | править код]
- Живой чертёж
- Weisstein, Eric W. Orthocenter (англ.) на сайте Wolfram MathWorld.
- Bernard Gibert Circumcubic K006 (недоступная ссылка)
- Clark Kimberling, «Encyclopedia of triangle centers».
- Weisstein, Eric W. «Orthocentric System.» From MathWorld–A Wolfram Web Resource. [1]
Точка пересечения высот треугольника


4.2
Средняя оценка: 4.2
Всего получено оценок: 416.
4.2
Средняя оценка: 4.2
Всего получено оценок: 416.
Точка пересечения высот треугольника относится к одной из трех замечательных точек треугольника. Замечательными эти точки зовутся не за красоту, а за отношение к золотому сечению треугольника, которое характеризует данную фигуру.

Опыт работы учителем математики – более 33 лет.
Высота
Что такое высота? Высота это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника (может получиться, что высота будет падать на продолжение стороны, как это бывает с тупоугольными треугольниками).
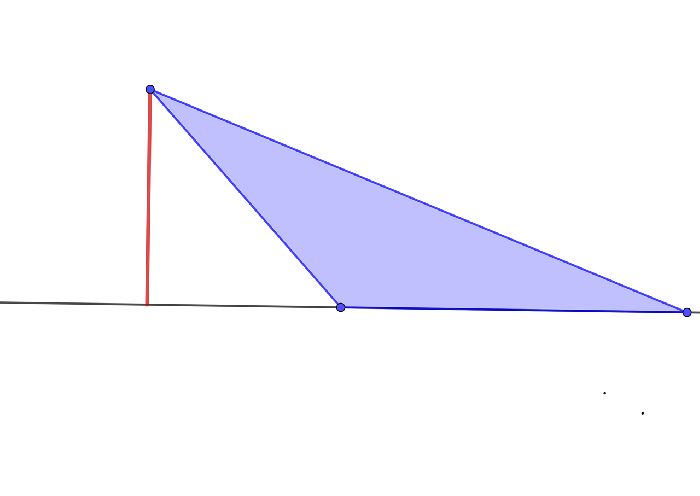
Точка пересечения высот
У любого треугольника есть три высоты, и они всегда пересекаются в одной точке. Эта точка является одним из 3 центров треугольника и зовется ортоцентром.
Еще со времен Древней Греции приставкой «орто» обозначали перпендикуляр. Ортогоналями звались перпендикулярные прямые.
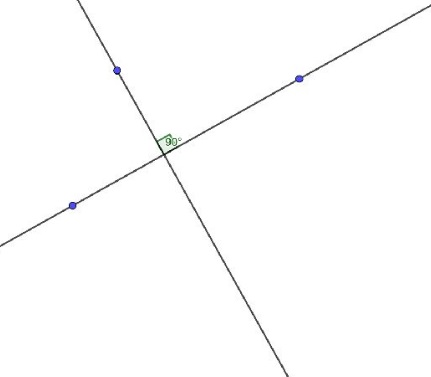
Ортоцентр имеет три варианта расположения в зависимости от вида треугольника:
- Внутри фигуры. В остроугольных треугольниках точка пересечения высот всегда находится внутри фигуры. Это обусловлено тем, что все высоты в таком треугольнике внутренние.
- Совпадает с вершиной. Этот случай характерен для прямоугольных треугольников. В таких треугольниках две из трех высот будут совпадать со сторонами. Если быть точнее, то совпадающие стороны это катеты. Остается одна высота, которая будет опускаться из вершины при остром угле. Именно эта вершина и будет ортоцентром треугольника.
- Вне фигуры. Внешнее расположение ортоцентра возможно только в тупоугольном треугольнике. Для того, чтобы получить ортоцентр такого треугольника, иногда потребуется продлить высоты до пересечения с внешней высотой. Почему? Потому что внешняя высота проходит за пределами треугольника и опускается на продолжение одной из сторон, а две внутренние стороны всегда ограничены треугольником. Поэтому без дополнительных построений ортоцентр тупоугольного треугольника не найти.
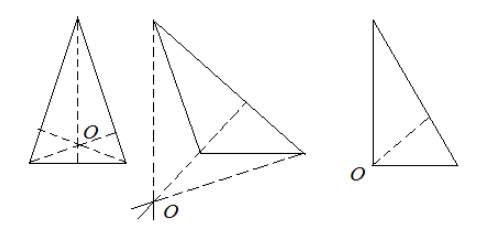
Золотое сечение треугольника
Золотое сечение треугольника это маленький треугольник внутри фигуры, который определяется как пересечение трех центров треугольника.
Три центра треугольника это:
- Точка пересечения биссектрис
- Точка пересечения высот
- Точка пересечения медиан.
Золотое сечение иногда может вырождаться в прямую или даже точку. В равнобедренном треугольнике точка пересечения высот и медиан совпадает, в результате для построения золотого сечения понадобится только 2 точки и золотое сечение выродится в отрезок.
О центрах треугольника существует целая онлайн энциклопедия. Список центров треугольника и свойств каждого из них был начат Карлом Кемберлингом в 1994 году. Онлайн ресурс пополняется все новыми и новыми данными по мере их открытия в высшей математике. В школьном курсе рассматривается только 3 центра треугольника.
В правильном треугольнике и вовсе каждая высота будет совпадать с соответствующей медианой, биссектрисой и высотой. Значит, все три центра треугольника совпадут, и золотым сечением треугольника будет – точка.
Обратите внимание, что нельзя составить уравнение точки пересечения высот треугольника. Можно составить только уравнение прямой. Например, составить два уравнения высот, затем приравнять их и найти координату точки пересечения.

Что мы узнали?
Мы узнали, в каких построениях участвует точка пересечения высот треугольника. Поговорили о случаях, когда эта точка совпадает с другими центрами треугольника, выяснили особенности расположения ортоцентра в разных видах треугольников.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 416.
А какая ваша оценка?
Чтобы найти ортоцентр треугольника, можно воспользоваться калькулятором, где следует внести координаты. В автоматическом режиме с помощью формул произведется расчет. Можно также все расчеты произвести самостоятельно.
Например, имеются следующие данные точек:
А – 4,3;
В – 0,5;
С – 3,-6.
Первое , что необходимо найти наклон сторон, который обозначается – m , используется формула :
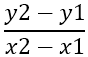
Из этого следует:
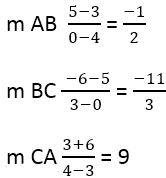
Далее необходимо найти наклон перпендикулярных сторон, для этого используется формула:
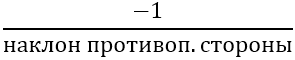
Имеем:
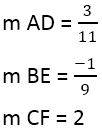
Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:
y-y1 = m(x-x1) y-3 = 3/11(x-4)
С помощью упрощения, имеем: 3х – 11у=-21
Для линии ВЕ, где точка 0,5, а наклон -1/9, имеем 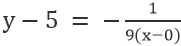
Упрощение дает: х+9у=45.
И последние линии CF, где точка 3, -6, а наклон 2, имеем уравнение y+6 = 2(x-3).
И упрощение, 2x — y = 12.
Если решить два из трех уравнений будут найдены значения х и у. Для данного примера:
Значение х = 8,05263;
Значение у = 4,10526.
Которые в данном случае являются координатами искомого Ортоцентра.

