Содержание:
Экстремум функции
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при 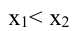
Если дифференцируемая функция у = f(x) на отрезке 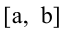 возрастает (убывает), то ее производная на этом отрезке
возрастает (убывает), то ее производная на этом отрезке 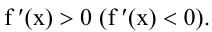
Точка 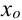 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 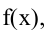 если существует окрестность точки
если существует окрестность точки 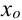 для всех точек которой верно неравенство
для всех точек которой верно неравенство 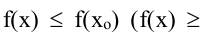
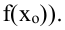
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – ее экстремумами.
Необходимые условия экстремума. Если точка хо является точкой экстремума функции 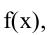 то либо
то либо 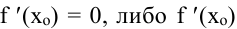 не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть
не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть 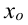 – критическая точка. Если f'(х) при переходе через точку
– критическая точка. Если f'(х) при переходе через точку  меняет знак плюс на минус, то в точке
меняет знак плюс на минус, то в точке  функция имеет максимум, в противном случае – минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.
функция имеет максимум, в противном случае – минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.
Второе достаточное условие. Пусть функция 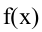 имеет производную f'(х) в окрестности точки
имеет производную f'(х) в окрестности точки  и вторую производную
и вторую производную 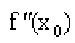 в самой точке
в самой точке  . Если
. Если 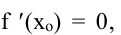
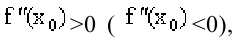 то точка
то точка  является точкой локального минимума (максимума) функции f(x). Если же
является точкой локального минимума (максимума) функции f(x). Если же 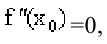 то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке 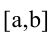 функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка
функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка 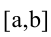 .
.
Пример:
Найти экстремумы функции 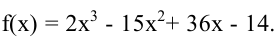
Решение:
Так как 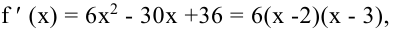 то критические точки функции
то критические точки функции 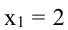 и
и 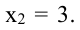 Экстремумы могут быть только в этих точках. Так как при переходе через точку
Экстремумы могут быть только в этих точках. Так как при переходе через точку 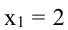 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку
производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку 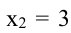 производная меняет знак минус на плюс, поэтому в точке
производная меняет знак минус на плюс, поэтому в точке 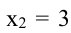 у функции минимум. Вычислив значения функции в точках
у функции минимум. Вычислив значения функции в точках 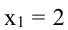 и
и 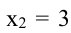 найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
Пример:
Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение:
Обозначим стороны площадки через 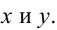 Площадь площадки равна
Площадь площадки равна 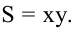 Пусть у – это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому
Пусть у – это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому 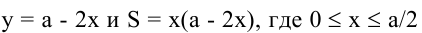 (длина и ширина площадки не могут быть отрицательными).
(длина и ширина площадки не могут быть отрицательными). 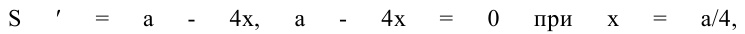 откуда
откуда 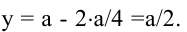 Поскольку
Поскольку 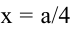 – единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При
– единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При 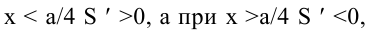 значит, в точке
значит, в точке 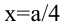 функция S имеет максимум. Значение функции
функция S имеет максимум. Значение функции 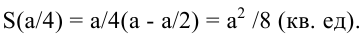
Поскольку S непрерывна на 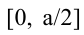 и ее значения на концах
и ее значения на концах 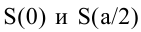 равны нулю, то найденное значение будет наибольшим значением функции.
равны нулю, то найденное значение будет наибольшим значением функции.
Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.
Пример:
Требуется изготовить закрытый цилиндрический бак вместимостью 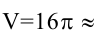
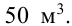 Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение:
Площадь полной поверхности цилиндра равна 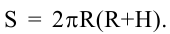 Мы знаем объем цилиндра
Мы знаем объем цилиндра 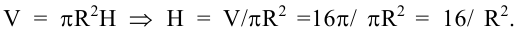 Значит,
Значит, 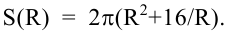 Находим производную этой функции:
Находим производную этой функции: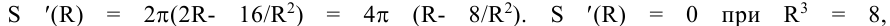 следовательно,
следовательно, 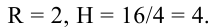
Экстремумы функции
Введём несколько новых понятий. Окрестностью точки 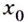 называется любой промежуток, для которого
называется любой промежуток, для которого 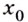 является внутренней точкой.
является внутренней точкой.
Точка 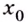 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 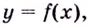 если для всех
если для всех 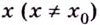 из некоторой окрестности точки
из некоторой окрестности точки 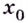 выполняется неравенство
выполняется неравенство 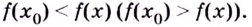
Точки минимума и максимума обозначают 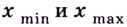 соответственно.
соответственно.
Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их: 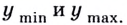
Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.
Например, для функции 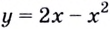 точка
точка  является точкой максимума (рис. 77). Её максимум:
является точкой максимума (рис. 77). Её максимум: 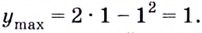
Для функции 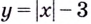 точка
точка 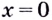 является точкой минимума (рис. 78). Её минимум:
является точкой минимума (рис. 78). Её минимум: 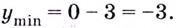
Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: 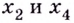 — точки максимума;
— точки максимума; 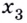 и
и 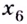 — точки минимума.
— точки минимума.
Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки. Это — необходимое условие существования экстремума.
Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.
Пусть функция 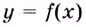 непрерывна на промежутке
непрерывна на промежутке 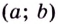 и
и 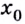 — её критическая точка,
— её критическая точка, 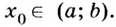 Тогда: точка
Тогда: точка 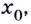 при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.
при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.
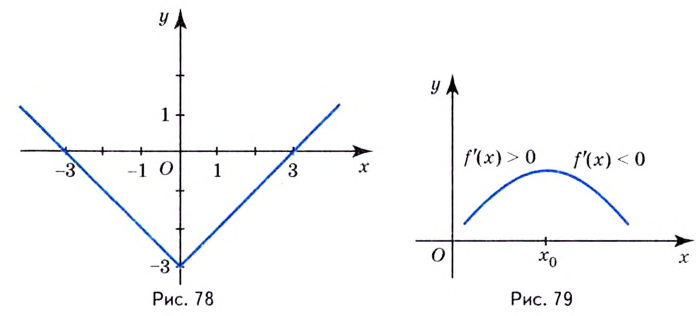
Действительно, если производная функции 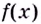 отрицательная, то при переходе через точку
отрицательная, то при переходе через точку 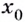 возрастание функции изменяется на убывание (рис. 79). В этом случае
возрастание функции изменяется на убывание (рис. 79). В этом случае 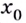 — точка максимума. Если же при переходе через точку
— точка максимума. Если же при переходе через точку 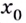 убывание функции изменяется на возрастание, то
убывание функции изменяется на возрастание, то 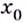 — точка минимума (рис. 80).
— точка минимума (рис. 80).
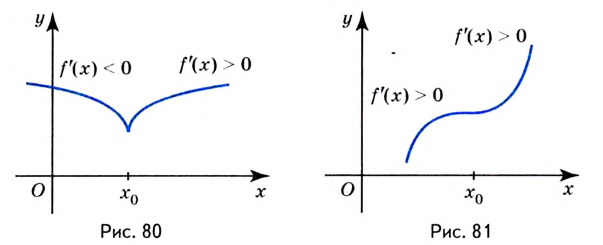
Если же производная функции в точке 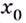 равна нулю, а слева и справа от
равна нулю, а слева и справа от 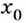 производная функции положительная (рис.81) или слева и справа отрицательная, то
производная функции положительная (рис.81) или слева и справа отрицательная, то 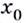 не является точкой экстремума.
не является точкой экстремума.
- Заказать решение задач по высшей математике
Пример №552
Найдите точки экстремума и экстремальные значения функции 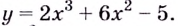
Решение:
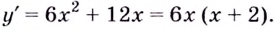
Критические точки функции: 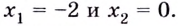 При переходе через точку
При переходе через точку 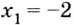 производная меняет знаке
производная меняет знаке 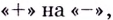 поэтому
поэтому 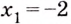 —точка максимума. При переходе через точку
—точка максимума. При переходе через точку 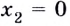 производная меняет знак с
производная меняет знак с 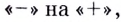 поэтому
поэтому 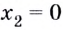 — точка минимума (рис. 82).
— точка минимума (рис. 82).
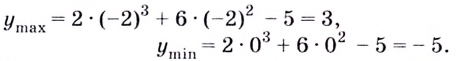
Ответ. 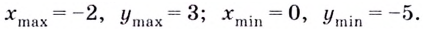
Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.
Чтобы исследовать функцию, можно пользоваться следующей схемой:
- найти область определения функции;
- исследовать функцию на чётность, нечётность, периодичность;
- найти точки пересечения графика функции с осями координат;
- исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
- найти точки экстремума и экстремальные значения функции;
- найти асимптоты графика функции;
- построить график функции.
Пример №553
Исследуйте функцию 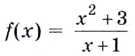 и постройте её график.
и постройте её график.
Решение:
Область определения функции — все действительные числа, кроме 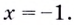 Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.
Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.
Уравнение 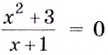 не имеет решений, поэтому график функции не пересекает ось
не имеет решений, поэтому график функции не пересекает ось 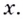 Ось
Ось 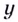 он пересекает в точке с ординатой
он пересекает в точке с ординатой 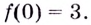
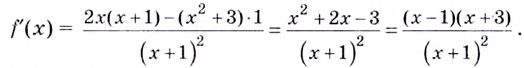
Критические точки: 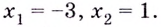
Составим и заполним таблицу.

На промежутках 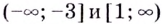 функция возрастает, на промежутках
функция возрастает, на промежутках 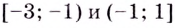 функция убывает.
функция убывает.  — точка максимума,
— точка максимума, 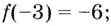
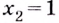 —точка минимума,
—точка минимума, 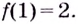
Область значений функции: 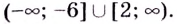
График функции имеет вертикальную асимптоту  так как
так как 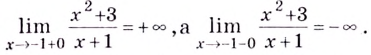
График этой функции изображён на рисунке 83.
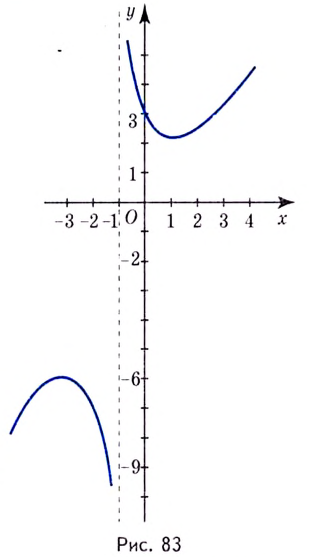
Пример №554
Может ли нечётная функция иметь экстремум в точке 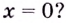 А чётная функция?
А чётная функция?
Решение:
Нечётная функция не может. Если в окрестности точки 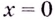 функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки
функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки  Чётная функция может. Например, функция
Чётная функция может. Например, функция 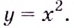
Пример №555
Существуют ли такие числа 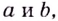 при которых имеет экстремум функция
при которых имеет экстремум функция 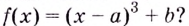
Решение:
При любых действительных значениях 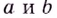
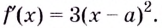 В каждой точке
В каждой точке 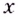 производная данной функции неотрицательная. Функция
производная данной функции неотрицательная. Функция 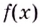 возрастает на
возрастает на 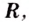 поэтому не может иметь экстремумов.
поэтому не может иметь экстремумов.
Ответ. Не существуют.
Пример №556
Исследуйте функцию 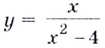 и постройте её график.
и постройте её график.
Решение. 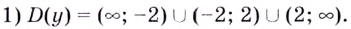
2) Функция — нечётная, поскольку 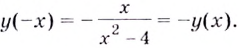
Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке 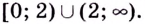
3) если 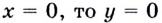 — график пересекает оси координат только в точке
— график пересекает оси координат только в точке 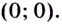
4) Найдём производную функции:
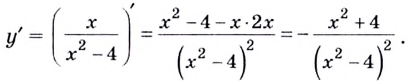
Очевидно, что 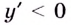 для всех х из области определения. Следовательно, функция убывает на каждом из промежутков
для всех х из области определения. Следовательно, функция убывает на каждом из промежутков 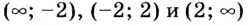 и не имеет максимумов и минимумов.
и не имеет максимумов и минимумов.
Для более точного построения вычислим значение функции в нескольких точках:
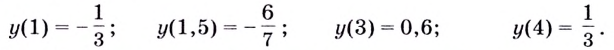
График функции имеет вертикальные асимптоты 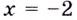 и
и 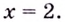 (Убедитесь самостоятельно.)
(Убедитесь самостоятельно.)
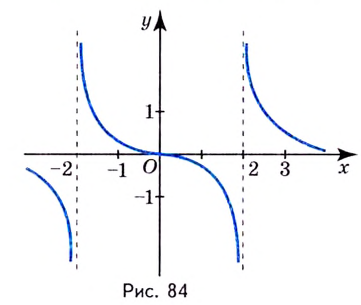
График функции изображён на рисунке 84.
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Функция y=f(x) будет возрастать на интервале x, когда при любых x1∈X и x2∈X , x2>x1неравенство f(x2)>f(x1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Функция y=f(x) считается убывающей на интервале x, когда при любых x1∈X, x2∈X, x2>x1 равенство f(x2)>f(x1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a;b), где х=а, х=b, точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x.
Основные свойства элементарных функций типа y=sinx – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале -π2; π2, тогда возрастание на отрезке имеет вид -π2; π2.
Точки экстремума, экстремумы функции
Точка х0 называется точкой максимума для функции y=f(x), когда для всех значений x неравенство f(x0)≥f(x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается ymax.
Точка х0 называется точкой минимума для функции y=f(x), когда для всех значений x неравенство f(x0)≤f(x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида ymin.
Окрестностями точки х0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [a;b]. Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х=b.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Пусть задана функция y=f(x), которая дифференцируема в ε окрестности точки x0, причем имеет непрерывность в заданной точке x0. Отсюда получаем, что
- когда f'(x)>0 с x∈(x0-ε; x0) и f'(x)<0 при x∈(x0; x0+ε), тогда x0 является точкой максимума;
- когда f'(x)<0 с x∈(x0-ε; x0) и f'(x)>0 при x∈(x0; x0+ε), тогда x0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком, то есть с + на -, значит, точка называется максимумом;
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком с – на +, значит, точка называется минимумом.
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Найти точки максимума и минимума заданной функции y=2(x+1)2x-2.
Решение
Область определения данной функции – это все действительные числа кроме х=2. Для начала найдем производную функции и получим:
y’=2x+12x-2’=2·x+12’·(x-2)-(x+1)2·(x-2)'(x-2)2==2·2·(x+1)·(x+1)’·(x-2)-(x+1)2·1(x-2)2=2·2·(x+1)·(x-2)-(x+2)2(x-2)2==2·(x+1)·(x-5)(x-2)2
Отсюда видим, что нули функции – это х=-1, х=5, х=2, то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х=-2, х=0, х=3, х=6.
Получаем, что
y'(-2)=2·(x+1)·(x-5)(x-2)2x=-2=2·(-2+1)·(-2-5)(-2-2)2=2·716=78>0, значит, интервал -∞; -1 имеет положительную производную. Аналогичным образом получаем, что
y'(0)=2·(0+1)·0-50-22=2·-54=-52<0y'(3)=2·(3+1)·(3-5)(3-2)2=2·-81=-16<0y'(6)=2·(6+1)·(6-5)(6-2)2=2·716=78>0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х=-1 функция будет непрерывна, значит, производная изменит знак с + на -. По первому признаку имеем, что х=-1 является точкой максимума, значит получаем
ymax=y(-1)=2·(x+1)2x-2x=-1=2·(-1+1)2-1-2=0
Точка х=5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
ymin=y(5)=2·(x+1)2x-2x=5=2·(5+1)25-2=24
Графическое изображение

Ответ: ymax=y(-1)=0, ymin=y(5)=24.
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x0, этим и упрощает вычисление.
Найти точки максимума и минимума функции y=16×3=2×2+223x-8.
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
-16×3-2×2-223x-8, x<016×3-2×2+223x-8, x≥0
После чего необходимо найти производную:
y’=16×3-2×2-223x-8′, x<016×3-2×2+223x-8′, x>0y’=-12×2-4x-223, x<012×2-4x+223, x>0
Точка х=0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y’x→0-0=lim yx→0-0-12×2-4x-223=-12·(0-0)2-4·(0-0)-223=-223lim y’x→0+0=lim yx→0-012×2-4x+223=12·(0+0)2-4·(0+0)+223=+223
Отсюда следует, что функция непрерывна в точке х=0, тогда вычисляем
lim yx→0-0=limx→0-0-16×3-2×2-223x-8==-16·(0-0)3-2·(0-0)2-223·(0-0)-8=-8lim yx→0+0=limx→0-016×3-2×2+223x-8==16·(0+0)3-2·(0+0)2+223·(0+0)-8=-8y(0)=16×3-2×2+223x-8x=0=16·03-2·02+223·0-8=-8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
-12×2-4x-223, x<0D=(-4)2-4·-12·-223=43×1=4+432·-12=-4-233<0x2=4-432·-12=-4+233<0
12×2-4x+223, x>0D=(-4)2-4·12·223=43×3=4+432·12=4+233>0x4=4-432·12=4-233>0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
y'(-6)=-12×2-4x-223x=-6=-12·-62-4·(-6)-223=-43<0y'(-4)=-12×2-4x-223x=-4=-12·(-4)2-4·(-4)-223=23>0y'(-1)=-12×2-4x-223x=-1=-12·(-1)2-4·(-1)-223=236<0y'(1)=12×2-4x+223x=1=12·12-4·1+223=236>0y'(4)=12×2-4x+223x=4=12·42-4·4+223=-23<0y'(6)=12×2-4x+223x=6=12·62-4·6+223=43>0
Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x=-4-233, x=0, x=4+233, тогда отсюда точки максимума имеют значениx=-4+233, x=4-233
Перейдем к вычислению минимумов:
ymin=y-4-233=16×3-22+223x-8x=-4-233=-8273ymin=y(0)=16×3-22+223x-8x=0=-8ymin=y4+233=16×3-22+223x-8x=4+233=-8273
Произведем вычисления максимумов функции. Получим, что
ymax=y-4+233=16×3-22+223x-8x=-4+233=8273ymax=y4-233=16×3-22+223x-8x=4-233=8273
Графическое изображение

Ответ:
ymin=y-4-233=-8273ymin=y(0)=-8ymin=y4+233=-8273ymax=y-4+233=8273ymax=y4-233=8273
Второй признак экстремума функции
Если задана функция f'(x0)=0, тогда при ее f”(x0)>0 получаем, что x0 является точкой минимума, если f”(x0)<0, то точкой максимума. Признак связан с нахождением производной в точке x0.
Найти максимумы и минимумы функции y=8xx+1.
Решение
Для начала находим область определения. Получаем, что
D(y): x≥0x≠-1⇔x≥0
Необходимо продифференцировать функцию, после чего получим
y’=8xx+1’=8·x’·(x+1)-x·(x+1)'(x+1)2==8·12x·(x+1)-x·1(x+1)2=4·x+1-2x(x+1)2·x=4·-x+1(x+1)2·x
При х=1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х=1. Получаем:
y”=4·-x+1(x+1)2·x’==4·(-x+1)’·(x+1)2·x-(-x+1)·x+12·x'(x+1)4·x==4·(-1)·(x+1)2·x-(-x+1)·x+12’·x+(x+1)2·x'(x+1)4·x==4·-(x+1)2x-(-x+1)·2x+1(x+1)’x+(x+1)22x(x+1)4·x==-(x+1)2x-(-x+1)·x+1·2x+x+12x(x+1)4·x==2·3×2-6x-1x+13·x3⇒y”(1)=2·3·12-6·1-1(1+1)3·(1)3=2·-48=-1<0
Значит, использовав 2 достаточное условие экстремума, получаем, что х=1 является точкой максимума. Иначе запись имеет вид ymax=y(1)=811+1=4.
Графическое изображение

Ответ: ymax=y(1)=4..
Третье достаточное условие экстремума
Функция y=f(x) имеет ее производную до n-го порядка в ε окрестности заданной точки x0 и производную до n+1-го порядка в точке x0. Тогда f'(x0)=f”(x0)=f”'(x0)=…=fn(x0)=0.
Отсюда следует, что когда n является четным числом, то x0 считается точкой перегиба, когда n является нечетным числом, то x0 точка экстремума, причем f(n+1)(x0)>0, тогда x0 является точкой минимума, f(n+1)(x0)<0, тогда x0 является точкой максимума.
Найти точки максимума и минимума функции yy=116(x+1)3(x-3)4.
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y’=116x+13′(x-3)4+(x+1)3x-34’==116(3(x+1)2(x-3)4+(x+1)34(x-3)3)==116(x+1)2(x-3)3(3x-9+4x+4)=116(x+1)2(x-3)3(7x-5)
Данная производная обратится в ноль при x1=-1, x2=57, x3=3. То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y”=116x+12(x-3)3(7x-5)’=18(x+1)(x-3)2(21×2-30x-3)y”(-1)=0y”57=-368642401<0y”(3)=0
Значит, что x2=57 является точкой максимума. Применив 3 достаточный признак, получаем, что при n=1 и f(n+1)57<0.
Необходимо определить характер точек x1=-1, x3=3. Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y”’=18(x+1)(x-3)2(21×2-30x-3)’==18(x-3)(105×3-225×2-45x+93)y”'(-1)=96≠0y”'(3)=0
Значит, x1=-1 является точкой перегиба функции, так как при n=2 и f(n+1)(-1)≠0. Необходимо исследовать точку x3=3. Для этого находим 4 производную и производим вычисления в этой точке:
y(4)=18(x-3)(105×3-225×2-45x+93)’==12(105×3-405×2+315x+57)y(4)(3)=96>0
Из выше решенного делаем вывод, что x3=3 является точкой минимума функции.
Графическое изображение

Ответ: x2=57 является точкой максимума, x3=3 – точкой минимума заданной функции.
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2,  из этого промежутка выполняется неравенство
из этого промежутка выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .
.
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .
.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2,  из этого промежутка выполняется неравенство
из этого промежутка выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
2) Найти f’ (x).
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
промежутках.
5) Сделать выводы о монотонности функции и точках ее
экстремума.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
- Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
- Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
- найти экстремальные точки функции, принадлежащие отрезку,
- найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
- выбрать из полученных значений максимальное и минимальное.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежуток монотонности функции у=х2 -8х +5
Решение: Найдем производную заданной функции: у’=2x-8
2x-8=0

х=4
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции: 
Найдем нули производной: 
х=-2,5
Определим знаки производной функции и изобразим на рисунке поведение функции:

Ответ: -2,5 точка min
№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc
Ответ: V=12 мc
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.

Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Ответ: 3
Содержание:
- Критические точки и экстремумы функции
- Теорема Ферма (Необходимое условие существовании экстремумов)
- Достаточное условие существования экстремума
- Задача пример №117
- Задача пример №118
- Задача пример №119
- Задача пример №120
- Задача пример №121
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений  равных
равных 
 угловой коэффициент касательной к графику равен 0. Т.e.
угловой коэффициент касательной к графику равен 0. Т.e.  . Эти точки являются критическими точками функции.
. Эти точки являются критическими точками функции.
2. В точках  функция не имеет производной. Эти тоже критические точки функции.
функция не имеет производной. Эти тоже критические точки функции.

3. Для рассматриваемой нами функции критические точки 
 делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки
делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки  – критические точки, которые не изменяют возрастание и убывание (или наоборот).
– критические точки, которые не изменяют возрастание и убывание (или наоборот).
По графику видно, что в точках внутреннего экстремума  производная функции равна нулю, а в точке
производная функции равна нулю, а в точке  производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.
производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.

Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке  производная функции
производная функции  равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.


Достаточное условие существования экстремума
Пусть функция  непрерывна на промежутке
непрерывна на промежутке  и
и  . Если
. Если  является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
1 )  слева от точки
слева от точки  положительна, а справа – отрицательна, то точка
положительна, а справа – отрицательна, то точка  является точкой максимума.
является точкой максимума.
2)  слева от
слева от  отрицательна, а справа – положительна, то точка
отрицательна, а справа – положительна, то точка  является точкой минимума
является точкой минимума
3)  с каждой стороны от точки
с каждой стороны от точки  имеет одинаковые знаки, то точка
имеет одинаковые знаки, то точка  не является точкой экстремума.
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции  на отрезке
на отрезке  записываются как
записываются как  и
и  .
.
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.

Задача пример №117
Для функции  определите максимумы и минимумы и схематично изобразите график.
определите максимумы и минимумы и схематично изобразите график.
Решение:
Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции: 
2. Критические точки функции: 
3. Точки  и
и  разбивают область определения функции на три промежутка.
разбивают область определения функции на три промежутка.
Проверим знак  на интервалах, выбрав пробные точки:
на интервалах, выбрав пробные точки:
 для интервала
для интервала 
 для интервала
для интервала 
 для интервала
для интервала 
Интервал  Пробные точки
Пробные точки 
Знак 
 Возрастание и убывание
Возрастание и убывание 
При  имеем
имеем  . (-1;3) – максимум
. (-1;3) – максимум
При  имеем
имеем  (1;-1) – минимум
(1;-1) – минимум
4. Используя полученные для функции  данные и найдя координаты нескольких дополнительных точек, построим график функции.
данные и найдя координаты нескольких дополнительных точек, построим график функции.


Задача пример №118
Найдите наибольшее и наименьшее значение функции  на отрезке [-1;2].
на отрезке [-1;2].
Решение:
Сначала найдем критические точки. Так как  , то критические точки можно найти из уравнения
, то критические точки можно найти из уравнения  . Критическая точка
. Критическая точка  не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке
не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке  и на концах отрезка.
и на концах отрезка.

Из этих значений наименьшее – 4, наибольшее 12. Таким образом: 
Задача пример №119
Найдите экстремумы функции  .
.
Решение:
1. Производная функции: 
2. Критические точки:  ,
, 
3. Интервалы, на которые критические точки делят область определения функции: 
Проверим знак  на интервалах, выбрав пробные точки.
на интервалах, выбрав пробные точки.
Для промежутка  возьмем
возьмем 
Для промежутка (0; 1,5) возьмем 
Для промежутка  возьмем
возьмем 
Интервал 
Пробные точки 
Знак 
 Возрастание-убывание
Возрастание-убывание 
Используя полученную для функции  информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами
информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами  и
и  касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.
касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.


• Функция  на промежутке
на промежутке  возрастает.
возрастает.
• Точка  критическая точка функции
критическая точка функции  , но не является экстремумом.
, но не является экстремумом.
• Функция  на промежутке [0; 1,5] возрастает.
на промежутке [0; 1,5] возрастает.
• Функция  на промежутке
на промежутке  убывает.
убывает.
• 
Задача пример №120
Найдите экстремумы функции 
Решение:
1. Производная 
2. Критические точки: для этого надо решить уравнение  или найти точки, в которых производная не существует. В точке
или найти точки, в которых производная не существует. В точке  функция не имеет конечной производной. Однако точка
функция не имеет конечной производной. Однако точка  принадлежит области определения. Значит, точка
принадлежит области определения. Значит, точка  является критической точкой функции.
является критической точкой функции.
3. Промежутки, на которые критическая точка делит область определения функции:  и
и 
Определим знак  , выбрав пробные точки для каждого промежутка:
, выбрав пробные точки для каждого промежутка:
Для  возьмем
возьмем  Для
Для  возьмем
возьмем 
Интервал  Пробные точки
Пробные точки 
Знак 

Возрастание-убывание 
• Функция  на промежутке
на промежутке  убывает.
убывает.
• Функция  на промежутке
на промежутке  возрастает.
возрастает.
• 
Задача пример №121
По графику функции производной  схематично изобразите график самой функции.
схематично изобразите график самой функции.

Решение:
Производная  в точке
в точке  равна нулю, а при
равна нулю, а при  отрицательна, значит, на интервале
отрицательна, значит, на интервале  функция убывающая. При
функция убывающая. При  производная положительна, а это говорит о том, что функция
производная положительна, а это говорит о том, что функция  на промежутке
на промежутке  возрастает. Точкой перехода от возрастания к убыванию функции является точка
возрастает. Точкой перехода от возрастания к убыванию функции является точка  . Соответствующий график представлен на рисунке.
. Соответствующий график представлен на рисунке.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Экстремумы функции двух переменных. Производная по направлению
- Доказательство неравенств
- Системы уравнений
- Максимальные и минимальные значения функции
- Действия с корнями
- Отрицательное биномиальное распределение
- Длина дуги кривой
- Вычислить несобственный интеграл
- Градиент функции: пример решения
- Интеграл натурального логарифма
