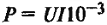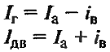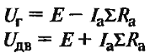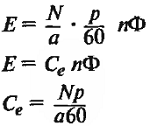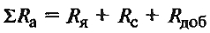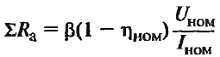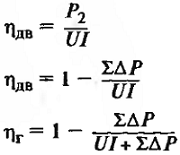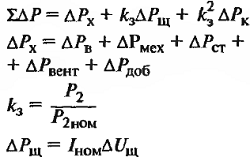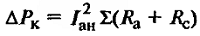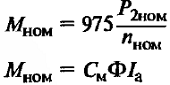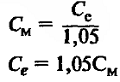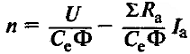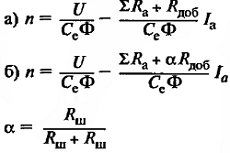Двигатель с параллельным возбуждением



Электрические машины постоянного тока.
Генератор с параллельным возбуждением.
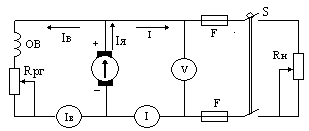
Ток отдаваемый генератором в сеть:
Эдс. генератора: Е= U+Iя ∙Rя.
Мощность отдаваемая сети: Р2 = U∙I =I 2 ∙R
Мощность приводного двигателя: Р1 = Р2/ η
Мощность потерь в обмотке якоря:
Мощность потерь в обмотке возбуждения:
Рв = U ∙Iв = I 2 в∙ Rв
Суммарные потери: ΣР = Р1 – Р2 .
Коэффициент полезного действия генератора:
η = Р2/Р1 = U∙I / (U∙I+ ΣР)
Двигатель с параллельным возбуждением.
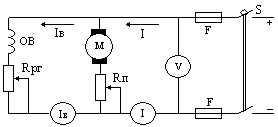
Ток двигателя: I = Iя + Iв
Напряжение двигателя: U = E + Iя ∙Rя.
Мощность потребляемая от сети: Р1 = U∙I
Момент на валу двигателя:
Коэффициент полезного действия двигателя:
Пример 6.1.Генератор постоянного тока с параллельным возбуждением развивает номинальное напряжение Uн =220 В. Генератор нагружен на нагрузку Rн = 2,2 Ом. Сопротивление обмотки якоря Rя = 0,2 Ом, обмотки возбуждения Rв =220 Ом. КПД генератора η = 0,87. Определить следующие величины:
1.ток нагрузки; 2. ток якоря; 3. ток возбуждения; 4. эдс генератора;
5.полезную мощность; 6. потребляемую мощность; 7. суммарные потери в генераторе; 8. потери в обмотке якоря; 9. потери в обмотке возбуждения.
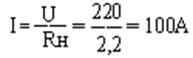
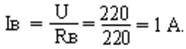
3.Ток якоря: Iя = I – Iв = 100 – 1= 99 А.
Е = U+ Iя ∙Rя = 220 + 99∙0,1 = 229,9 В.
Р2 = Uн∙I = 220∙100 = 22000 Вт = 22 кВт.
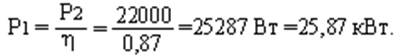
7.Суммарные потери в генераторе:
ΣР = Р1– Р2 = 25,87 – 22 = 3,87 кВт.
8.Потери в обмотке якоря:
Ря = Iя 2 ∙Rя = 99 2 ∙0,2 = 1960,2 Вт.
9.Потери в обмотке возбуждения:
Рв = Uн∙Iв = 220∙1 = 220 Вт.
Ответ: I = 100А; Iв = 1 А; Iя = 99 А; Е = 229,9 В; Р2 = 22 кВт;
Р1 = 25,87 кВт; ΣР = 3,87 кВт; Ря = 1960,2 Вт; Рв = 220 Вт.
Пример 6.2.Рис.8.2.Двигатель постоянного токапараллельного возбуждения работает от сети Uн = 220 В. Частота вращения якоря n2 = 1450 об/мин. Ток двигателя I = 500 А, противо–эдс якоря Е = 202 В, сопротивление обмотки возбуждения Rв = 44 Ом. Кпд двигателя
η = 0,88. Определить:1.ток возбуждения; 2.ток якоря; 3. сопротивление обмотки якоря; 4.потребляемую мощность; 5.полезную мощность на валу; 6 Суммарные потери в двигателе; 7.потери в обмотке якоря; 8.потери в обмотке якоря; 9.вращающий момент на валу.
1. Ток возбуждения:
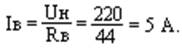
Iя = I – Iв = 500 –5 = 495 А.
3. Сопротивление обмотки якоря:
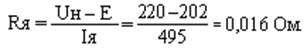
4. Потребляемая мощность от сети:
Р1 = Uн∙I = 220 ∙500 = 110 000 Вт = 110 кВт.
5. Полезная мощность на валу:
Р2 = P1∙ η = 110 ∙ 0,87 = 95,7 кВт.
6. Суммарные потери в двигателе:
ΣР = Р1 – P2 = 110 – 95,7 = 14,3 кВт.
7. Потери в обмотке возбуждения:
Pв = Uн∙Iв = 220∙5 = 1100 Вт =1,1 кВт.
8. Потери в обмотке якоря:
Ря = Iя 2 ∙ Rя =495 2 ∙0,016 = 3920,4 Вт = 3,92 кВт.
9. Вращающий момент на валу:
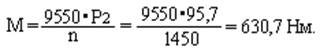
Ответ: Iв = 5 А,Iя = 495 А, Rя = 0,016 Ом,Р1 = 110 кВт, Р2 = 95,7 кВт,
ΣР = 14,3 кВт, Pв = 1,1 кВт, Ря =3,92 кВт М = 630,7 Нм.
Источник
Расчет и схема соединений обмоток якоря машины постоянного тока
Петлевые обмотки якоря. Основные понятия. Обмотка якоря машины постоянного тока представляет собой замкнутую систему проводников, определенным образом уложенных на сердечнике якоря и присоединенных к коллектору.
Элементом обмотки якоря является секция(катушка), присоединенная к двум коллекторным пластинам. Расстояние между пазовыми частями секции должно быть равно или мало отличаться от полюсного деления 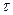 (рисунок 59):
(рисунок 59):
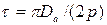 .
.
Здесь 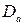 – диаметр сердечника якоря, мм.
– диаметр сердечника якоря, мм.
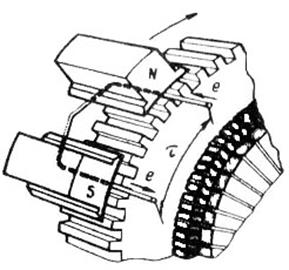
Рисунок 59 – Расположение пазовых сторон секции на сердечнике якоря
Обмотки якоря обычно выполняют двухслойными. Они характеризуются следующими параметрами: числом секций S; числом пазов (реальных) Z; числом секций, приходящихся на один паз, 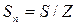 ;числом витков секции
;числом витков секции 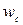 ; числом пазовых сторон в обмотке N;числом пазовых сторон в одном пазу
; числом пазовых сторон в обмотке N;числом пазовых сторон в одном пазу 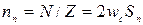 . Верхняя пазовая сторона одной секции и нижняя пазовая сторона другой секции, лежащие в одном пазу, образуют элементарный паз.Число элементарных пазов в реальном пазе
. Верхняя пазовая сторона одной секции и нижняя пазовая сторона другой секции, лежащие в одном пазу, образуют элементарный паз.Число элементарных пазов в реальном пазе  определяется числом секций, приходящихся на один паз:
определяется числом секций, приходящихся на один паз: 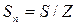 (рисунок 60).
(рисунок 60).
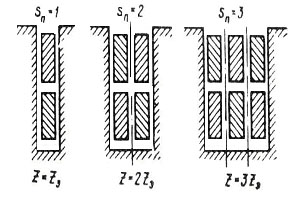
Рисунок 60 – Элементарные пазы
Схемы обмоток якоря делают развернутыми, при этом все секции показывают одновитковыми. В этом случае каждой секции, содержащей две пазовые стороны, соответствует один элементарный паз. Концы секций присоединяют к коллекторным пластинам, при этом к каждой пластине присоединяют начало одной секции и конец другой, т. е. на каждую секцию приходится одна коллекторная пластина. Таким образом, для обмотки якоря справедливо
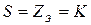 ,
,
где 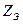 – число элементарных пазов;
– число элементарных пазов;
К –число коллекторных пластин в коллекторе.
Число секций, приходящихся на один реальный паз, определяется отношением 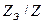 .
.
Простая петлевая обмотка якоря. В простой петлевой обмотке якоря каждая секция присоединена к двум рядом лежащим коллекторным пластинам. При укладке секций на сердечнике якоря начало каждой последующей секции соединяется с концом предыдущей, постепенно перемещаясь при этом по поверхности якоря (и коллектора) так, что за один обход якоря укладывают все секции обмотки. В результате конец последней секции оказывается присоединенным к началу первой секции, т. е. обмотка якоря замыкается.
На рисунке 61, а, б изображены части развернутой схемы простой петлевой обмотки, на которых показаны шаги обмотки – расстояния между пазовыми сторонами секций по якорю: первый частичный шаг по якорю  ,второй частичный шаг по якорю
,второй частичный шаг по якорю 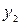 и результирующий шаг по якорю
и результирующий шаг по якорю 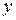 .
.
Если укладка секций обмотки ведется слева направо по якорю, то обмотка называется правоходовой(рисунок 61, а), а если укладка секций ведется справа налево, то обмотка называется левоходовой(рисунок 61, 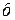 ).Для правоходовой обмотки результирующий шаг
).Для правоходовой обмотки результирующий шаг
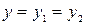 .
.
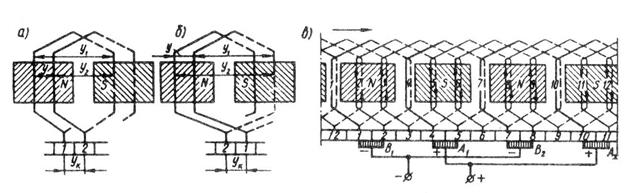
Рисунок 61 – Простая петлевая обмотка:
а – правоходовая; б – левоходовая; в – развернутая схема
Расстояние между двумя коллекторными пластинами, к которым присоединены начало и конец одной секции, называют шагом обмотки по коллектору ук . Шаги обмотки по якорю выражают в элементарных пазах, а шаг по коллектору – в коллекторных делениях (пластинах).
Начало и конец каждой секции в простой петлевой обмотке присоединены к рядом лежащим коллекторным пластинам, следовательно, 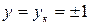 , где знак плюс соответствует правоходовой обмотке, а знак минус – левоходовой.
, где знак плюс соответствует правоходовой обмотке, а знак минус – левоходовой.
Для определения всех шагов простой петлевой обмотки достаточно рассчитать первый частичный шаг по якорю:
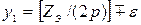 ,
,
где 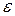 – некоторая величина, меньшая единицы, вычитая или суммируя которую получают значение шага
– некоторая величина, меньшая единицы, вычитая или суммируя которую получают значение шага  , равное целому числу.
, равное целому числу.
Второй частичный шаг обмотки по якорю
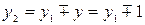 .
.
Пример 1. Рассчитать шаги и выполнить развернутую схему простой петлевой обмотки якоря для четырехполюсной машины (2 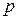 = 4) постоянного тока. Обмотка правоходовая, содержит 12 секций.
= 4) постоянного тока. Обмотка правоходовая, содержит 12 секций.
Решение. Первый частичный шаг по якорю
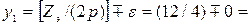 3 паза.
3 паза.
Второй частичный шаг по якорю
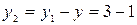 =2паза.
=2паза.
Прежде чем приступить к выполнению схемы обмотки, необходимо отметить и пронумеровать все пазы и секции, нанести на предполагаемую схему контуры магнитных полюсов и указать их полярность (рисунок 61, в). При этом нужно иметь в виду, что отмеченный на схеме контур является не полюсом, а зеркальным отображением полюса, находящегося над якорем. Затем изображают коллекторные пластины и наносят на схему первую секцию, пазовые части которой располагают в пазах 1 и 4. Коллекторные пластины, к которым присоединены начало и конец этой секции, обозначают 1 и 2. Затем нумеруют все остальные пластины и наносят на схему остальные секции (2, 3, 4 и т. д.). Последняя секция 12 должна замкнуть обмотку, что будет свидетельствовать о правильном выполнении схемы.
Далее на схеме изображают щетки. Расстояние между щетками А и В должно быть равно К/(2 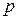 ) = 12/4 = 3, т. е. должно соответствовать полюсному делению. Что же касается расположения щеток на коллекторе, то при этом следует руководствоваться следующим. Предположим, что электрический контакт обмотки якоря с внешней цепью осуществляется не через коллектор, а непосредственно через пазовые части обмотки, на которые наложены «условные» щетки (рисунок 62, а). В этом случае наибольшая ЭДС машины соответствует положению «условных» щеток на геометрической нейтрали. Но так как коллекторные пластины смещены относительно пазовых сторон соединенных с ними секций на 0,5
) = 12/4 = 3, т. е. должно соответствовать полюсному делению. Что же касается расположения щеток на коллекторе, то при этом следует руководствоваться следующим. Предположим, что электрический контакт обмотки якоря с внешней цепью осуществляется не через коллектор, а непосредственно через пазовые части обмотки, на которые наложены «условные» щетки (рисунок 62, а). В этом случае наибольшая ЭДС машины соответствует положению «условных» щеток на геометрической нейтрали. Но так как коллекторные пластины смещены относительно пазовых сторон соединенных с ними секций на 0,5 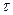 (рисунок 62, б),то, переходя к реальным щеткам, их следует расположить на коллекторе по оси главных полюсов, как это показано на рисунке 61, в.
(рисунок 62, б),то, переходя к реальным щеткам, их следует расположить на коллекторе по оси главных полюсов, как это показано на рисунке 61, в.
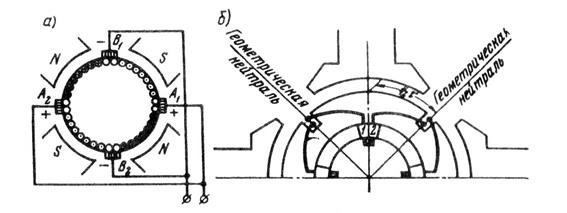
Рисунок 62 – Расположение щеток: а) условных; б) реальных
При определении полярности щеток предполагают, что машина работает в генераторном режиме и ее якорь вращается в направлении стрелки (см. рисунок 61, в). Воспользовавшись правилом «правой руки», находят направление ЭДС (тока), наведенной в секциях. В итоге получаем, что щетки 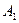 и
и 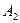 ,от которых ток отводится во внешнюю цепь, являются положительными, а щетки
,от которых ток отводится во внешнюю цепь, являются положительными, а щетки 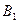 и B2 – отрицательными. Щетки одинаковой полярности присоединяют параллельно к выводам соответствующей полярности.
и B2 – отрицательными. Щетки одинаковой полярности присоединяют параллельно к выводам соответствующей полярности.
Параллельные ветви обмотки якоря. Если проследить за прохождением тока в секциях обмотки якоря (см. рисунок 61, в), то можно заметить, что обмотка состоит из четырех участков, соединенных параллельно друг другу и называемых параллельными ветвями.Каждая параллельная ветвь содержит несколько последовательно соединенных секций с одинаковым направлением тока в них. Распределение секций в параллельных ветвях показано на электрической схеме обмотки (рисунок 63). Эту схему получают из развернутой схемы обмотки (см. рисунок 61, 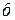 ) следующим образом. На листе бумаги изображают щетки и имеющие с ними контакт коллекторные пластины, как это показано на рисунке 63. Затем совершают обход секций обмотки начиная с секции 1, которая оказывается замкнутой накоротко щеткой
) следующим образом. На листе бумаги изображают щетки и имеющие с ними контакт коллекторные пластины, как это показано на рисунке 63. Затем совершают обход секций обмотки начиная с секции 1, которая оказывается замкнутой накоротко щеткой 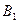 . Далее идут секции 2 и 3,которые образуют параллельную ветвь. Таким же образом обходят все остальные секции. В результате получаем схему с четырьмя параллельными ветвями, по две секции в каждой ветви.
. Далее идут секции 2 и 3,которые образуют параллельную ветвь. Таким же образом обходят все остальные секции. В результате получаем схему с четырьмя параллельными ветвями, по две секции в каждой ветви.
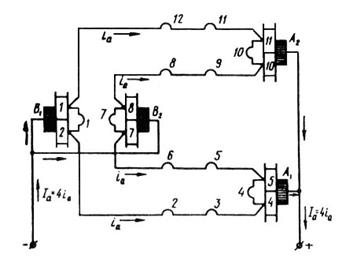
Рисунок 63 – Электрическая схема обмотки рисунка 61, в.
Из полученной схемы следует, что ЭДС обмотки якоря определяется значением ЭДС одной параллельной ветви, тогда как значение тока обмотки определяется суммой токов всех ветвей обмотки:
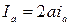 ,
,
где 2 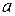 – число параллельных ветвей обмотки якоря;
– число параллельных ветвей обмотки якоря;
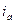 – ток одной параллельной ветви.
– ток одной параллельной ветви.
В простой петлевой обмотке число параллельных ветвей равно числу главных полюсов машины:2 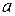 = 2
= 2 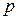 .
.
Нетрудно заметить, что число параллельных ветвей в обмотке якоря определяет значение основных параметров машины – тока и напряжения.
Пример 2. Шестиполюсная машина постоянного тока имеет на якоре простую петлевую обмотку из 36 секций. Определить ЭДС и силу тока в обмотке якоря машины, если в каждой секции наводится ЭДС 10 В, а сечение провода секции рассчитано на ток не более 15 А.
Решение. Число параллельных ветвей в обмотке 2 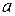 = 2
= 2 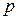 = 6, при этом в каждой параллельной ветви
= 6, при этом в каждой параллельной ветви 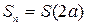 = 36/6 = 6 секций. Следовательно, ЭДС обмотки якоря
= 36/6 = 6 секций. Следовательно, ЭДС обмотки якоря 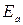 = 6∙10 = 60 В, а допустимый ток машины
= 6∙10 = 60 В, а допустимый ток машины 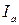 = 6∙15 = 90 А.
= 6∙15 = 90 А.
Если бы машина при прочих неизменных условиях имела восемь полюсов, то ее ЭДС уменьшилась бы до 40 В, а ток увеличился бы до 120 А.
Сложная петлевая обмотка. При необходимости получить петлевую обмотку сбольшим числом параллельных ветвей, как это требуется, например, низковольтных машинах постоянного тока, применяют сложную петлевую обмотку. Такая обмотка представляет собой несколько (обычно две) простых петлевых обмоток, уложенных на одном якоре и присоединенных к одному коллектору. Число параллельных ветвей в сложной петлевой обмотке 2 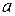 = 2
= 2 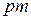 ,где т – число простых петлевых обмоток, из которых составлена сложная обмотка (обычно т = =2). Ширина щеток при сложной петлевой обмотке принимается такой, чтобы каждая щетка одновременно перекрывала т коллекторных пластин, т. е. столько пластин, сколько простых обмоток в сложной. При этом простые обмотки оказываются присоединенными параллельно друг другу. На рисунке 64 показана развернутая схема сложной петлевой обмотки, состоящей из двух простых (т = 2): 2
,где т – число простых петлевых обмоток, из которых составлена сложная обмотка (обычно т = =2). Ширина щеток при сложной петлевой обмотке принимается такой, чтобы каждая щетка одновременно перекрывала т коллекторных пластин, т. е. столько пластин, сколько простых обмоток в сложной. При этом простые обмотки оказываются присоединенными параллельно друг другу. На рисунке 64 показана развернутая схема сложной петлевой обмотки, состоящей из двух простых (т = 2): 2 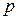 = 4;
= 4; 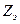 = 16. Результирующий шаг обмотки по якорю и шаг по коллектору сложной петлевой обмотки принимают равным у = ук = т.
= 16. Результирующий шаг обмотки по якорю и шаг по коллектору сложной петлевой обмотки принимают равным у = ук = т.
Пример 3. Четырехполюсная машина имеет сложную петлевую обмотку якоря из 16 секций. Выполнить развернутую схему этой обмотки, приняв т –2.
Решение. Шаги обмотки:
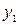 =
= 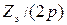 =16/4 = 4 паза;
=16/4 = 4 паза;
у = 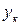 = 2 паза;
= 2 паза;
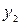 =
= 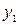 – у = 4–2 = 2 паза.
– у = 4–2 = 2 паза.
Сначала располагаем все секции одной из простых обмоток (секции с нечетными номерами: 1, 3, 5 и т. д.), а концы этих секций присоединением к нечетным пластинам коллектора (рисунок 64). Затем располагаем на якоре секции другой петлевой обмотки с номерами 2, 4, 6 и т. д. Изображаем на схеме щетки шириной в два коллекторных деления. Число параллельных ветвей обмотки 2 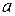 = 2
= 2 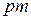 = 4·2 = 8.
= 4·2 = 8.
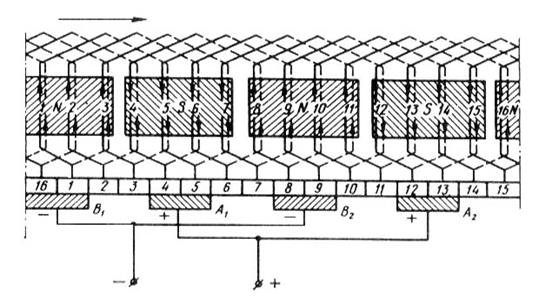
Рисунок 64 – Развернутая схема сложной петлевой обмотки
Источник
Обозначив
![]()
и
используя соотношение

(С-7)
можно
найти активный ток якоря как

; (С-8)
В случае расчетов
без использования ЭВМ допускается
использовать приближенное выражение

(С-9)
3.2. Определение результирующей э.Д.С. И м.Д.С.
Для
результирующей э.д.с.
в
соответствии с диаграммой рис. С-1 имеем

(С-11)
При
расчетах без использования ЭВМ допускается
приближенное выражение
![]()
(С-11)
Разумеется,
что в выражения (10) или (11) следует
подставить
![]()
,
т.е. учитывать опережающий характер
тока якоря.
Для
определения результирующей М.Д.С.
используется «характеристика холостого
хода» синхронной машины (рис.С-2)
Эта
зависимость достаточно точно
апроксимируется выражением
![]()
(С-12),
которое следует
использовать для точного определения
Э.Д.С. по М.Д.С. (или наоборот).
3.3 Определение составляющих м.Д.С. Якоря
Из векторной
диаграммы рис. С-1 следует, что

(C-13)
При
невозможности использования ЭВМ
допускается полагать
0
Тогда угол
выбега ротора в
соответствии с диаграммой может быть
найден как

(с-14)
Приближенное
выражение для :

(С-15)
допускается
при расчетах без использования ЭВМ.
Составляющие
тока якоря ( по осям) определяются как

(С-16)
Необходимо
помнить, что в выражениях (с-13)….(С-17)
составляющая тока якоря
![]()
подставляется
отрицательной; углы
и также являются
отрицательными.
3.4. Определение тока возбуждения
Из диаграммы
рис. С-1 следует, что
![]()
(С-18)
Здесь в
соответствии с (С-16)
![]()
является
также отрицательным.
4. Варианты исполнения сд критерия оптимальности
Математическая
модель СД (6) позволяет, таким образом,
при выбранном значении Рвн
(с учетом разновидности исполнения,
т.е. н и cos
н)
определить основные величины, описывающие
рабочий режим (для любой мощности на
валу Рвт до Рвм):
-
величину тока якоря
;
-
величину тока возбуждения
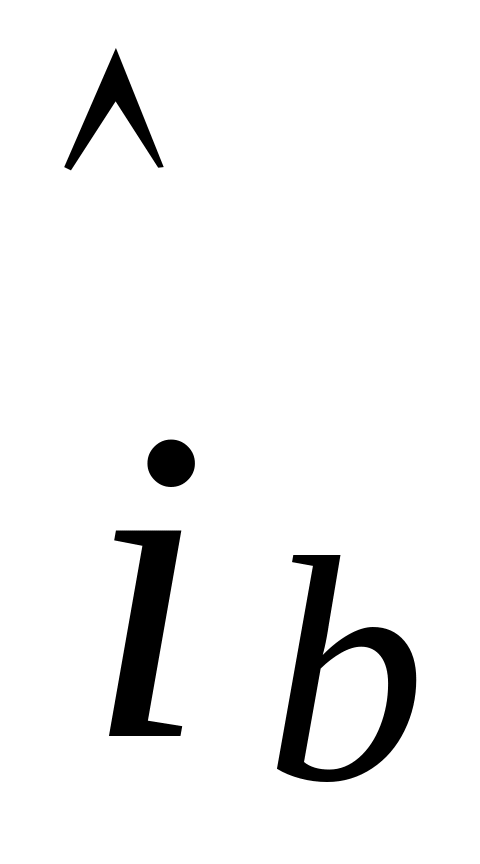
; -
суммарную мощность потерь
энергии ( с учетом потерь на возбуждение)
![]()
(С-19)
Разумеется, что
определение всех этих (и вспомогательных)
величин возможно, если заданы параметры
СД:
-
значение сопротивлений
и

; -
величина мощности потерь

и

(для іb=іb0);
-
коэффициент приведения
м.д.с. якоря кd;
кaq.
Данные о
параметрах десяти вариантов СД, имеющихся
в распоряжении проектанта, приведены
в таблице С-2.
Считается, что
все варианты имеют равную стоимость
(независимо от разновидности, т.е.
значений н и
cos н)
и одинаковые характеристики холостого
хода (типа С-17), а также
каd=0,9
и каq=0,6
Отличие вариантов
состоит прежде всего в величине
предельного допустимого тока возбуждения
ibmax.
Обращаясь к кривой рис. С-2, можно заметить,
старшие варианты (позволяющие большее
перевозбуждение) обладают меньшей
степенью насыщения стали (поэтому у них
меньше рассеяние полей), но при этом
имеют большие значения сопротивления
якоря.
![]()
(С-20)
В качестве
показателей оптимальности варианта СД
следует использовать величину суммарных
потерь энергии
![]()
(С-21)
Так как по
условию проекта мощность на валу СД
изменяется случайно и может равновероятно
принимать значения Рb
:
![]()
;
то критерием оптимальности СД
можно считать среднее значение суммарной
мощности потерь энергии
![]()
Таким образом,
оптимальным вариантом СД данной
номинальной мощности Рвн
и разновидности (по значениям н
и cos н),
следует считать тот , для которого
выполняются условия:

(С-23)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение:
Потери мощности в цепи возбуждения
![]()
Ток в цепи возбуждения, присоединенной параллельно к цепи якоря,
![]()
Ток нагрузки
![]()
Ток в цепи якоря
![]()
Э. д. с. в обмотке якоря
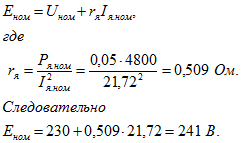
Ток в цепи возбуждения, составляющий 150% номинального тока,
![]()
Согласно характеристике холостого хода э. д. с, при этом равна 107% от номинальной э. д. с:
![]()
При холостом ходе контур цепи неразветвленный и его сопротивление
![]()
Таким образом, сопротивление обмотки возбуждения
![]()
При холостом ходе напряжение между зажимами машины можно считать равным э. д. с. Отсюда в последнем пункте задачи
![]()
Выразим эту э. д. с. в процентах от номинальной э. д. с:
![]()
Поэтому, пользуясь данными, приведенными ранее, путем интерполяции найдем, что для э. д. с. ![]() ток возбуждения
ток возбуждения
![]()
Сопротивление цепи возбуждения и якоря
![]()
откуда сопротивление регулировочного реостата
![]()
5. Генератор постоянного тока параллельного возбуждения имеет: номинальную мощность 14 кВт; номинальное напряжение 230 В; номинальный ток якоря 60,9 А; номинальную скорость вращения 1500 об/мин; сопротивление цепи якоря 0,17 Ом; сопротивление обмотки возбуждения 124 Ом; ток возбуждения при полной нагрузке и номинальном напряжении 1,21 А; ток возбуждения при холостом ходе и номинальном напряжении 0,9 А; коэффициент полезного действия 0,85. Генератор предполагается использовать в качестве двигателя при напряжении сети 220 В.
Определить скорость вращения при полной нагрузке и полезную мощность на валу двигателя.
Решение:
Э. д. с. машины постоянного тока как в режиме генератора, так и в режиме двигателя пропорциональна магнитному потоку, скорости вращения якоря, причем коэффициентом пропорциональности служит некоторая постоянная величина ![]() , зависящая от конструктивных данных машины. Таким образом,
, зависящая от конструктивных данных машины. Таким образом,
![]()
Здесь![]() — э. д. с. машины в режиме генератора;
— э. д. с. машины в режиме генератора;![]() — э. д. с. машины в режиме двигателя (против э. д. с);
— э. д. с. машины в режиме двигателя (против э. д. с);![]() — скорости вращения в генераторном и двигательном режимах;
— скорости вращения в генераторном и двигательном режимах;![]() — магнитные потоки в режимах генератора и двигателя.
— магнитные потоки в режимах генератора и двигателя.
Постоянная ![]() в обеих формулах одна и та же. Отсюда получим выражение для скорости вращения двигателя:
в обеих формулах одна и та же. Отсюда получим выражение для скорости вращения двигателя:
![]()
Э. д. с. ![]() выразим следующим образом:
выразим следующим образом:
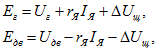
где ![]() — падение напряжения в щеточном контакте, которое принимается не зависящим от тока
— падение напряжения в щеточном контакте, которое принимается не зависящим от тока
якоря и равным 2 В (при холостом ходе машины ![]() ).
).
Подставляя числовые значения, получим:
![]()
Магнитные потоки определяются по характеристике холостого хода машины, в зависимости от тока возбуждения. Эта характеристика обычно задается графически и ее точное аналитическое выражение дать невозможно. Вид характеристики определяется нагрузками для магнитной цепи машины и свойствами примененных материалов. Вследствие стандартизации этих материалов и стремления использовать их наиболее полно как допускаемые магнитные нагрузки, так и свойства применяемых материалов колеблются в довольно узких пределах. Поэтому в современных электрических машинах характеристики холостого хода схожи между собой.
Если за единицу тока возбуждения принять ток, соответствующий номинальному напряжению при отсутствии нагрузки, за единицу магнитного потока — магнитный поток, соответствующий тому же напряжению, то характеристику холостого хода можно выразить в виде, практически пригодном для обычных современных электрических машин:
![]()
Здесь ток возбуждения i и соответствующий ему магнитный поток ![]() выражены в долях от величин, соответствующих номинальному напряжению машины в режиме генератора при отсутствии нагрузки, т. е. при разомкнутой цепи якоря:
выражены в долях от величин, соответствующих номинальному напряжению машины в режиме генератора при отсутствии нагрузки, т. е. при разомкнутой цепи якоря:
![]()
Ток возбуждения для двигательного режима можно легко определить исходя из сопротивления обмотки возбуждения и напряжения сети (предполагаем, что обмотка возбуждения включена непосредственно на напряжение сети без добавочных сопротивлений):
![]()
Зная токи возбуждения, выраженные в амперах при обоих режимах работы, определяем их в долях от тока возбуждения в режиме холостого хода:
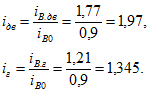
По приведенному выше уравнению находим магнитные потоки:
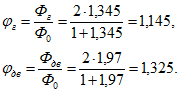
Отношение потоков
![]()
Подставляя полученные величины э. д. с. и отношение магнитных потоков в выражение для скорости вращения электродвигателя, получим
![]()
Модность на валу двигателя легко определить, мощность на входе в электродвигатель:
![]()
Следует заметить, что в эту величину входит лишь мощность якорной цепи без учета мощности цепи возбуждения.
Примем коэффициент полезного действия одинаковым как в режиме двигателя, так и в режиме генератора. Для приближенных расчетов это допустимо, так как в режиме двигателя увеличиваются потери энергии в обмотке возбуждения (увеличивается ток возбуждения), но из-за меньшей скорости вращения уменьшаются механические потери и потери в стали. Сумма потерь и, следовательно, коэффициент полезного действия изменяются незначительно.
Мощность в обмотке возбуждения
![]()
Следовательно, мощность при потреблении энергии от сети
![]()
а полезная мощность на валу двигателя
![]()
Допустим, что необходимо и в режиме двигателя сохранить скорость вращения 1500 об/мин. Для этого необходимо уменьшить магнитный поток двигателя, включив в цепь возбуждения добавочное сопротивление. Определим величину этого сопротивления. Ток якоря двигателя по условиям нагрева остается прежним, а противо-э. д. с. двигателя сохраняет свою величину ![]() . Из выражения
. Из выражения
![]()
считая ![]() можно определить необходимый магнитный поток двигателя в долях единицы:
можно определить необходимый магнитный поток двигателя в долях единицы:
![]()
Зная магнитный поток, легко определить соответствующий ему ток возбуждения:
![]()
или в амперах ![]()
Далее определяем добавочное сопротивление в цепи возбуждения ![]() , необходимое для получения тока возбуждения, обусловливающего заданный магнитный поток:
, необходимое для получения тока возбуждения, обусловливающего заданный магнитный поток:
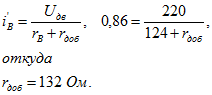
6. К шинам электростанции постоянного тока параллельно присоединены генератор (с параллельной обмоткой возбуждения) и аккумуляторная батарея (рис. 68). Внешняя характеристика генератора задана следующими числовыми значениями: ![]() . Аккумуляторная батарея состоит из 70 последовательно включенных элементов, причем для каждого элемента э. д. с. е = 2 в и внутреннее сопротивление
. Аккумуляторная батарея состоит из 70 последовательно включенных элементов, причем для каждого элемента э. д. с. е = 2 в и внутреннее сопротивление ![]() .
.
Определить:
1) напряжение ![]() на шинах, при котором э. д. с. аккумуляторной батареи будет скомпенсирована
на шинах, при котором э. д. с. аккумуляторной батареи будет скомпенсирована ![]() ;
;
2) токи нагрузки и генератора, а также напряжение ![]() при котором разрядный ток батареи составит 25% от тока приемников энергии.
при котором разрядный ток батареи составит 25% от тока приемников энергии.
Содержание
- Основные уравнения двигателя постоянного тока (ДПТ)
- Противо ЭДС двигателя Eя
- Ток якоря Iя
- Частота вращения якоря
- Электромагнитная мощность двигателя
- Электромагнитный момент
- Электродвижущая сила обмотки якоря
- Содержание
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА ОБМОТКИ ЯКОРЯ
- МОМЕНТ НА ВАЛУ МАШИНЫ
- МЕХАНИЧЕСКАЯ МОЩНОСТЬ МАШИНЫ ПОСТОЯННОГО ТОКА
- РЕАКЦИЯ ЯКОРЯ
Основные уравнения двигателя постоянного тока (ДПТ)

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.
В результате взаимодействия Iя тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.
Противо ЭДС двигателя Eя
При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС Eя направленная навстречу Iя. Поэтому эта ЭДС называется противо ЭДС и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.
Ce — постоянный коэффициент определяемой конструкцией двигателя.
Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.
где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :
- обмотки якоря
- добавочных полюсов
- обмотки возбуждения (для двигателей с последовательным возбуждением)
Ток якоря Iя
Выразим из формулы 2 ток якоря.
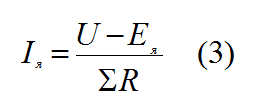
Частота вращения якоря
Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Электромагнитная мощность двигателя
Электромагнитный момент

где: ω = 2*π*f — угловая скорость вращения якоря, Cм — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М момент холостого хода;
Источник
Электродвижущая сила обмотки якоря
Содержание
ЭЛЕКТРОДВИЖУЩАЯ СИЛА ОБМОТКИ ЯКОРЯ
При вращении якоря генератора или двигателя в магнитном поле в его обмотке будет наводиться э. д. с.
Магнитная индукция в различных точках на окружности якоря имеет разные значения, следовательно, различны и э. д. с, наводимые в отдельных проводах обмотки якоря. Электродвижущая сила машины, равная сумме э. д. с, наводимых в проводах любой из параллельных ветвей обмотки якоря, может быть определена через среднее значение э. д. с. провода, умноженное на число проводов ветви.
Если магнитный поток одного полюса — Ф, то при числе полюсов машины 2р и поверхности якоря Sсреднее значение магнитной индукции на поверхности якоря
где d — диаметр якоря, а l — его длина.
Среднее значение э. д. с. в каждом из проводов при
скорости вращения якоря п об/мин
Обозначим число проводов обмотки якоря N, а число параллельных ветвей ее — 2 a. Тогда в каждой параллельной ветви обмотки якоря будет N/ a последовательно соединенных проводов. Электродвижущая сила, наведенная в каждое параллельной ветви обмотки якоря, а следовательно, н э. д. с. машины
Обозначив постоянную для данной машины величину N(p/(a•60)) через с Е , получим :
Таким образом, э. д. с. машины пропорциональна магнитному потоку и скорости вращения ее якоря.
Рис. 8-12. Поперечная реакция якоря. Рис. 8-13. Перераспределение магнитной индукции от реакция якоря.
МОМЕНТ НА ВАЛУ МАШИНЫ
Независимо от того, в каком режиме работает машина — генератором или электродвигателем, на каждый провод якоря действует электромагнитная сила
где B cp — среднее значение магнитное индукции; d и I — диаметр и длина якоря; Ф2 р — полный поток многополюсной машины;
I=I я/2 а — ток одной параллельной ветви, т. е. одного провода.
Полная сила, действующая на N проводов якоря по касательной к окружности якоря.
Если машина работает генератором, момент будет тормозной (М т); при работе ее электродвигателем момент будет вращающим ( М в). Момент равен произведению тока якоря и потока машины.
МЕХАНИЧЕСКАЯ МОЩНОСТЬ МАШИНЫ ПОСТОЯННОГО ТОКА
Электрическая машина преобразует механическую энергию в электрическую или электрическую в механическую. При этом механическая мощность
Подставляя сюда выражение для момента, получаем:
Таким образом, , развиваемая якорем машины механическая мощность равна ее электрической мощности, т.е. произведению электродвижущей силы и тока якоря. При работе машины генератором мощность EI я больше, чем мощность UI я, отдаваемая потребителю, так как Е > U. Когда машина работает электродвигателем и, значит, Е тогда мощность EI я меньше мощности UI я, подаваемой из сети. Эта разница мощностей численно равна мощности тепловых потерь I 2 r я в обмотке якоря.
РЕАКЦИЯ ЯКОРЯ
Когда машина работает генератором вхолостую, т. е. при I я = 0, магнитный поток возбуждения Ф B, создаваем мый н. с. F B , существует один и проходит от северного полюса к южному через якорь (рис. 8-12). В этом случае индукция В δ в воздушном зазоре, в пределах полюсного наконечника, остается практически постоянной.
Если генератор нагружен, т. е. по обмотке якоря проходит ток, якорь сам становится электромагнитом п его и. с. F я создает второй поток — поперечный поток
якоря Ф я. Он замыкается через воздушный зазор машины и поперек ее полюсов, уменьшая индукцию в воздушном зазоре В δ под одним краем полюса (левым у северного и правым у южного и увеличивая В δпод другим краем (правым у северного и левым у южного) (рис. 8-13). По отношению направлению вращения якоря можно сказать, что набегающий край полюса размагничивается, а сбегающий — намагничивается.
Суммарный поток машины Ф смещен в направлении вращения якоря; в ту же сторону смещена нейтраль машины, называемая в данном случае физической нейтралью (рис. 8-13). В результате поток Ф при нагрузке несколько уменьшается, так как вследствие насыщения стати размагничивание на набегающем краю полюса оказывается большим, чем намагничивание на сбегающем. Влияние н. с. якоря на величину магнитного потока машины при нагрузке называется реакцией якоря.
В современных машинах постоянного тока, нормального исполнения уменьшение магнитного потока под влиянием реакции якоря незначительно.
Главная опасность этого явления, как будет показано ниже, заключается в том, что магнитная индукция в воз-душном зазоре под краем полюса может сильно возрастать.
Если машина работает электродвигателем, то при направления тока в якоре, указанном на рис. 8-12, якорь будет вращаться в обратную сторону. Следовательно, реакция якоря будет сдвигать поток Ф и физическую нейтраль против хода якоря.
Статья на тему Электродвижущая сила обмотки якоря
Источник
Расчетные формулы параметров машин постоянного тока
В таблице 1 представлены расчетные формулы для определения основных параметров машин постоянного тока.
В данной таблице собраны все формулы, которые касаются расчета параметров машин постоянного тока.
Таблица 1 — Расчетные формулы для определения основных параметров машин постоянного тока
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Мощность, кВт |
|
I – ток машины, А; U – внешнее напряжение, В; |
| Ток генератора и двигателя, А |
|
Iа – ток якоря; Iв – ток параллельной обмотки возбуждения, А; |
| Внешнее напряжение, В |
|
∑Ra – сумма сопротивлений якорной цепи, Ом; Е – ЭДС машины, В; |
| ЭДС, В |
|
N – число проводников обмотки якоря; а – число пар параллельных ветвей в обмотке якоря; р – число пар полюсов; n – скорость вращения, об/мин. |
| Сопротивление якорной цепи, Ом |
|
Ф – магнитный поток пары полюсов, вебер; Rя, Rс, Rдоб. – сопротивления обмотки якоря, последовательной обмотки возбуждения и добавочных полюсов, Ом |
| Ориентировочной значение сопротивления цепи якоря, Ом |
|
Значение коэффициента β двигателей различного типа возбуждения: для независимого и параллельного возбуждения β=0,5; для смешанного β=0,6; для последовательного β=0,75; |
| КПД двигателя и генератора |
|
∑∆Р – суммарные потери в машине, кВт; |
| Суммарные потери, кВт |
|
∆Рх – потери холостого хода машины или постоянные потер, кВт; ∆Рв – потери на возбуждение, кВт; ∆Рмех. – механические потери на трение в подшипниках и о коллектор, кВт; ∆Рст. – магнитные потери в стали якоря, кВт; ∆Рвент. – вентиляционные потери, кВт; ∆Рдоб. – добавочные потери. В некомпенсированных машинах ∆Рдоб. = 1%Рном, в компенсированных 0,5%, кВт; kз – коэффициент загрузки; ∆Uщ = 2 В для графитных щеток; ∆Uщ = 0,6 В для металлографитных; |
| Переменные потери |
|
|
| Номинальный вращающий момент, кГм |
|
См – конструктивная постоянная момента; Ф – магнитный поток, вебер; |
| Расчетные коэффициенты для двигателя параллельного возбуждения |
|
|
| Скоростная характеристика двигателя |
|
|
| Искусственные скоростные характеристики |
|
а) искусственная скоростная характеристика при введении добавочного сопротивления Rдоб. последовательно в цепь якоря; б) искусственная скоростная характеристика двигателя при шунтировании якоря двигателя сопротивлением Rш; α – коэффициент шунтирования. |
Литература:
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
КПД генератора, параметры машин постоянного тока, ток генератора, ЭДС
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.