Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
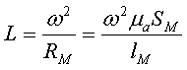
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле
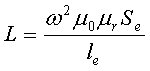
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
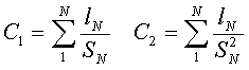
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
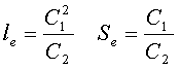
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
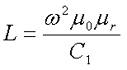
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
Расчёт катушки с тороидальным сердечником
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.
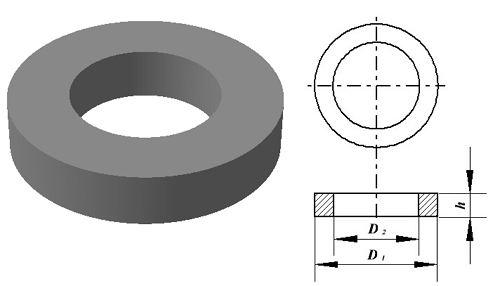
Тороидальный сердечник.
Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
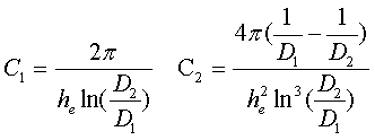
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.
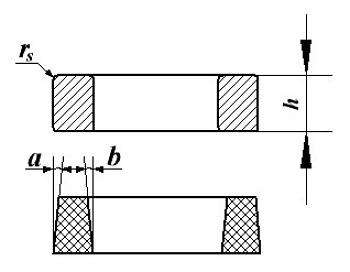
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs
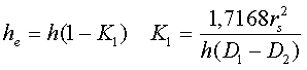
в) трапецеидальное поперечное сечение с острыми кромками
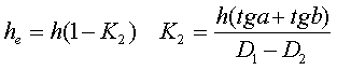
г) трапецеидальное поперечное сечение со скруглёнными кромками
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости
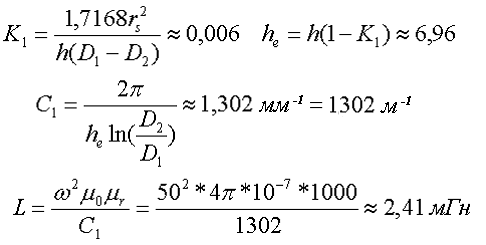
Расчёт катушки с П–образным сердечником прямоугольного сечения
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.
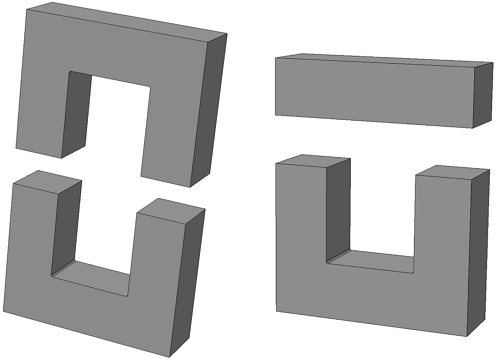
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника
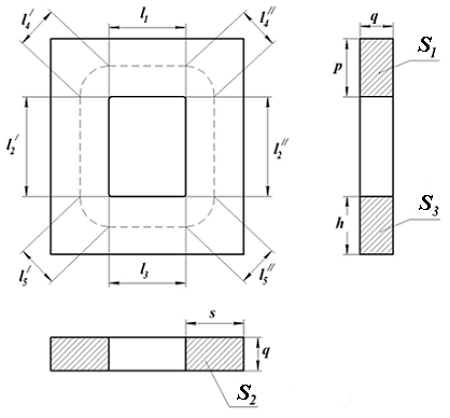
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
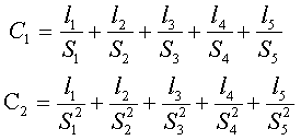
Неизвестные величины можно найти следующим образом
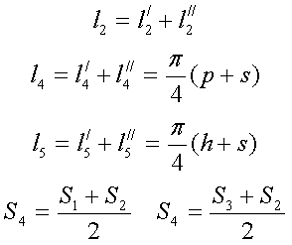
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.
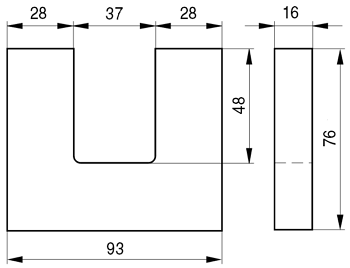
Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
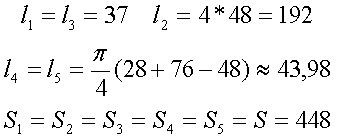
Таким образом коэффициент С1 и индуктивность L составят
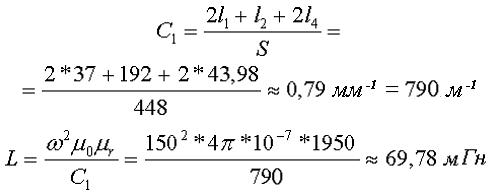
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей
П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.
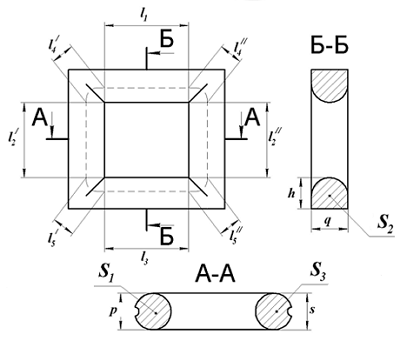
Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь
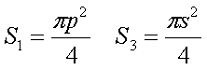
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.
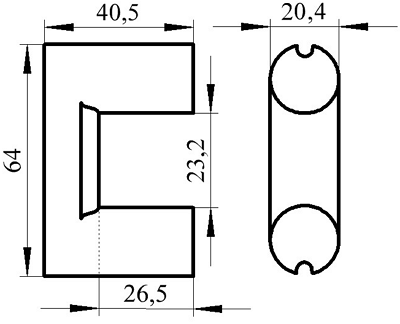
Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят
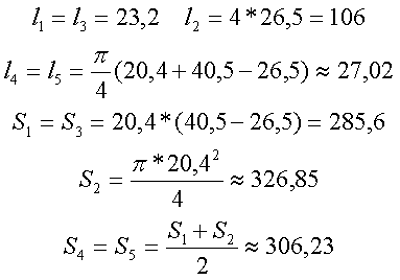
Таким образом коэффициент С1 и индуктивность L составят
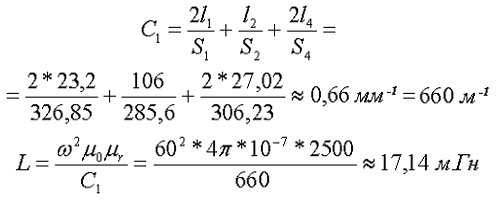
На сегодня всё. Продолжение смотри в следующей статье.
- Информация о материале
-
Опубликовано: 02 сентября 2013
-
Обновлено: 04 декабря 2022
-
Просмотров: 9584
Расчет тороидальной катушки индуктивности
Тороидальные катушки индуктивности без магнитного сердечника используются незаслуженно редко. Магнитное поле такой катушки при плотной намотке практически полностью сосредоточено внутри тора, благодаря чему такая конструкция имеет малое поле рассеяния и, соответственно, такая катушка мало подвержена влиянию внешних полей даже без экрана. Для расчета индуктивности тороида круглого поперечного сечения можно за основу взять формулу расчета индуктивности соленоида [2]. S необходимо заменить на площадь поперечного сечения тора, а l – на среднюю длину окружности тора
 |
[1] |
Где A – поперечное сечение тора, а R – средний радиус окружности тороида, μ0 – магнитная постоянная. Индуктивность в Генри, размеры в метрах.
Приложение Coil64 использует упрощенную формулу:
 |
[2] |
Индуктивность в микрогенри, размеры в сантиметрах, N – число витков катушки, R – средний радиус окружности тора, a – радиус намотки. Эта формула может быть использована для практических расчетов индуктивности тороидальной катушки круглого поперечного сечения. Дополнительные формулы расчета:
Где D1 D2 – наружный и внутренний диаметр тороидального каркаса, dw – диаметр провода.
Однако в радиолюбительской практике мы чаще имеем дело с тороидами, имеющими квадратное поперечное сечение как на изображении в шапке этой статьи, хотя при большом числе витков сечение такой катушки становится больше похожим на эллипс. Экспериментально было установлено, что расчет числа витков тороида с квадратным сечением лучше вести по эмпирическим формулам расчета катушки на ферритовом кольце, только магнитная проницаемость в этом случае принимается равной единице. Это и реализовано в программе Coil64.
-
Методики расчета индуктивности катушек
Основным
элементом катушек индуктивности является
токовод. Величина индуктивности
определяется конструкцией токовода и
его размерами.
Полная
индуктивность медного провода круглого
сечения длиной lПРи диаметромd0равна
(3.1)
Из
(3.1) следует, что индуктивность провода
уменьшается с ростом его диаметра. Это
свойство широко используют в УКВ
аппаратуре для уменьшения индуктивности
соединительных проводов за счет
увеличения их диаметра.
Если
одиночный проводник согнуть, например,
в кольцо, то его индуктивность уменьшится
из-за встречного направления токов в
соседних частях кольца. Однако, для
круглого кольца индуктивность будет
наибольшей по сравнению с индуктивностью
витка любой другой конфигурации,
поскольку круглый виток охватывает
наибольшую площадь, обеспечивая
наибольшее потокосцепление.
Индуктивность
круглого плоского витка диаметром Dиз провода круглого сечения длинойlПРи диаметромdПРравна
(3.2)
При
сворачивании проводника в несколько
витков wодинакового
диаметра образуется катушка, индуктивность
которой можно определить как суммарную
индуктивность всех витков с учетом
взаимоиндукцииMмежду
ними:
(3.3)
Индексы при Муказывают на взаимную индуктивность
между первым и вторым, вторым и третьим,
первым и третьим витками и т.д. Если
известен коэффициент связи, который
определяется равенством
,
(3.4)
то индуктивность
катушки с произвольным числом витков
определяется из
. (3.5)
Коэффициент связи
между витками, расположенными на
расстоянии τ, в однослойной катушке
определяется выражением
(3.6)
Для сплошной намотки
τ=d0.
Индуктивность
многослойной катушки незначительно
зависит от диаметра провода, так как
определяется в основном взаимоиндукцией
между витками.
Из-за трудности
определения коэффициента связи выражение
(3.5) обычно применяют для расчета катушек
индуктивности с небольшим числом витков
(обычно не более шести).
Для катушек с однородным
замкнутым магнитопроводом (с тороидальным
сердечником) выражение для определения
индуктивности принимает вид
, (3.7)
где μ– начальная магнитная
проницаемость сердечника (μ=1 для
диэлектрического каркаса или воздуха);
μ0=4π·10-7Гн/м – магнитная постоянная;
w– число витков обмотки;
S
– площадь поперечного сечения катушки;
– длина намотки катушки;
Таким
образом, увеличение индуктивности
катушки может быть достигнуто за счет
увеличения числа витков, магнитной
проницаемости сердечника, площади
поперечного сечения магнитопровода, а
также уменьшения длины намотки.
В
высокочастотных катушках замкнутый
магнитопровод как правило отсутствует,
поэтому индуктивность катушки будет
меньше, рассчитанной по (3.7). Для учета
рассеивания магнитного потока на краях
катушки вводится поправочный коэффициент
k, который зависит от
отношения диаметра катушки к длине
намотки
(3.8)
Для
практических расчетов однослойных
цилиндрических катушек, намотанных
виток к витку (рис.3.2 а),используют
выражение
, (3.9)
где
– коэффициент формы катушки, учитывающий
краевые эффекты;
μ– начальная магнитная
проницаемость сердечника (μ=1 для
катушек без магнитного сердечника);
μ0=4π·10-7Гн/м –
магнитная постоянная;
w– число витков обмотки;
– площадь поперечного сечения круглой
катушки;
D– диаметр катушки;
– длина намотки.
Для
практических расчетов однослойных
цилиндрических катушек без сердечника,
намотанных с принудительным шагом τ(рис.3.2 б),индуктивн
ость
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL
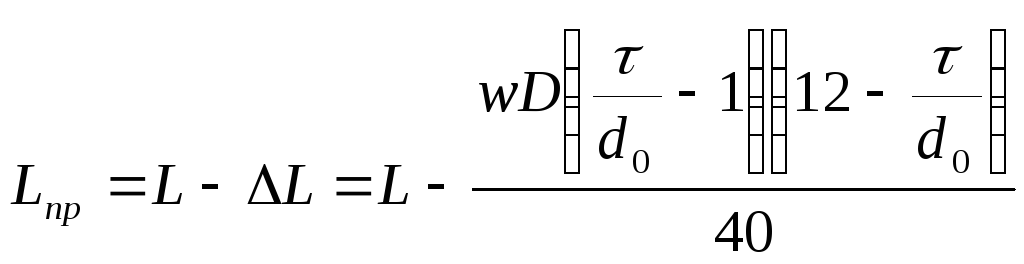, (3.10)
где τ– шаг намотки;
L–
индуктивность катушки, определенная
по (3.9) приμ=1.
Для
практических расчетов индуктивности
тороидальной однослойной катушки,
намотанной сплошным слоем на круглом
магнитном сердечнике прямоугольного
сечения (рис.3.2 в), используют
выражение
, (3.11)
где
– площадь поперечного сечения сердечника
тороида;
– средняя длина сердечника тороида;
D– внешний диаметр сердечника тороида;
d– внутренний диаметр сердечника тороида;
h– высота сердечника тороида.
Для практических
расчетов многослойных катушек без
сердечника(рис.3.2 г) используют
выражение
, (3.12)
г
деDCP
– средний диаметр катушки;
t– толщина катушки;
l– длина катушки.
Для
практических расчетов многослойных
секционированных катушек без сердечника
(рис.3.2 д) используют выражение
, (3.13)
где LC
– индуктивность одной секции катушки;
n– число секций;
kCB– коэффициент связи между смежными
секциями, зависящий от отношения
(рис.3.3);
b
– расстояние между секциями.
Для
практических расчетов плоских круглых
спиральных катушек (рис.3.2 е) используют
выражение
, (3.14)
где DBH,DH –внутренний и наружный диаметры
катушки, соответственно.
Для
практических расчетов плоских
квадратных спиральных катушек (рис.3.2
ж) используют выражение
, (3.15)
где АBH,АH
–внутренняя и наружная стороны
катушки, соответственно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
10.02.20165.15 Mб192.doc
- #
- #
- #
- #
- #
- #
Что такое катушка индуктивности
Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В — магнитное поле, Вб
I — сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I — сила тока в катушке , А
U — напряжение в катушке, В
R — сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 — это каркас катушки
2 — это витки катушки
3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Индуктивность и ее расчет:
Основным соотношением для магнитного поля является принцип непрерывности магнитного потока:
На рис. 1.12, а и б проиллюстрировано различие между потоком и потокосцеплением, причем число линий в условном масштабе равно величине потока.
Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб). Индуктивность уединенного контура, равная отношению потокосцепления к току:
пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн). Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:
устанавливающему связь между напряженностью магнитного поля и полным током I — алгебраической суммой токов, сцепляющихся с путем интегрирования. При этом положительное направление тока I связано с направлением dI обхода правилом правого винта. Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м. Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:
где Е — вектор напряженности наведенного в контуре электрического поля. Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем. Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.
Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром. При изменении тока в контуре изменяется потокосцепление ψL созданное этим током, и в контуре наводится э. д. с. самоиндукции
Индуктивность тороида и соленоида
Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ0, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.
Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.
Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г1 и г2, магнитная проницаемость материала µ.
По закону полного тока для окружности с радиусом
откуда
т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции
Поток в сердечнике тороида
а потокосцепление
Отсюда индуктивность тороида
Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность
где w0 — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,
Обычно в реальных тороидах отношение что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ0
где k
Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При = 0,1 коэффициент k — 0,96, поэтому при
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Индуктивность двухпроводной линии
Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г0, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ0. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.
Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса дает:
При интегрировании по окружности, лежащей внутри отдельного провода охватывается лишь часть LХ всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению
В воздухе между проводами на линии, соединяющей центры их сечений направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:
Эти же формулы справедливы и для т. е. снаружи линии, но здесь они дают разность полей.
Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:
Внутри правого провода соответственно,
На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ0. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.
На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,
Весь поток между проводами — внешний поток
одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому
а соответствующая ему внешняя индуктивность
Для большинства линий расстояние d между проводами значительно превышает радиус r0 проводов. В этом случае
Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r0 поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода
Так как поток dФi охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление
Весь поток между проводами — внешний поток
Соответственно, внутренняя индуктивность
Суммарная индуктивность линии
При медных или алюминиевых проводах () в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда
Для стальных проводов () основной частью потока является внутренний поток и индуктивность
практически не будет зависеть от расстояния между проводами.
Изготовление тороидальных катушек
Радиолюбители довольно широко применяют в своих конструкциях катушки индуктивности с тороидальными (кольцевыми) магнитопроводами. По сравнению с катушками с магнитопроводами других типов такие катушки имеют ряд преимуществ — высокую добротность, отсутствие внешних полей рассеяния, невосприимчивость к внешним магнитным полям и т. д.
Однако намотка катушек на тороидальных магнитопроводах сопряжена с известными трудностями, особенно при большом числе витков. Радиолюбители при намотке таких катушек обычно используют самодельные плоские шпули или челноки. Для облегчения изготовления катушек, содержащих большое число витков, иногда кольцевой магнитопровод (обычно он ферритовый) аккуратно разламывают на две части, наматывают на каждой из них половинное число витков, после чего половинки магнитопровода склеивают, а полуобмотки соединяют согласно-последовательно (т. е. конец одной с началом другой). Такому способу свойственны существенные недостатки: из-за механических воздействий значительно снижается начальная магнитная проницаемость материала магнитопровода, наличие немагнитных зазоров в местах склеивания уменьшает магнитную проницаемость — в результате эффективная магнитная проницаемость магнитопровода снижается на порядок, а то и более. Для получения требуемой индуктивности катушки приходится пропорционально увеличивать число её витков, в результате чего возрастает активное сопротивление обмотки и снижается её добротность. Из-за неравномерности распределения витков катушки по магнитопроводу магнитное поле уже не локализуется внутри катушки, дополнительное выпячивание магнитного поля из магнитопровода происходит в местах склеивания — увеличиваются внешние поля рассеяния, катушка требует экранирования.
Предлагаемый способ позволяет изготавливать катушки индуктивности на тороидальных (кольцевых) магнитопроводах с наружным диаметром 10 мм и менее, индуктивностью до нескольких генри с малыми трудовыми затратами. Этим способом можно изготавливать катушки с максимально достижимыми значениями индуктивности и добротности, полностью заполняя обмоткой окно магнитопровода.
Такого результата можно достичь, если катушку намотать высокочастотным обмоточным проводом (устаревшее название — литцендрат), представляющим собой жгут (пучок) изолированных одна от другой и скрученных вместе проволок диаметром 0,03—0,1 мм с наружной волокнистой шёлковой однослойной (марка ЛЭШО) или лавсановой (марка ЛЭЛО) изоляцией (если наруж ная изоляция состоит из двух слоев — соответственно ЛЭШД или ЛЭ/1Д). Проволок в пучке может быть от трех до нескольких сотен, но для поставленной цели наиболее пригодны провода с числом проволок 7—10 диаметром 0,05 или 0,07 мм, например, ЛЭШО или ЛЭЛО 10×0,05; 7×0,07; 10×0,07.
Суть способа заключается в том, что катушку наматывают сравнительно толстым проводом-жгутом, а затем составляющие его тонкие изолированные провода соединяют между собой согласно-последовательно, в результате чего требуемое число витков уменьшается в равное числу проводов раз. Технологический процесс состоит из трёх выполняемых последовательно операций: подготовки магнитопровода, собственно намотки и соединения проводов.
Подготовка магнитопровода заключается в тщательном скруглении острых кромок мелкозернистой наждачной бумагой во избежание повреждения изоляции тонкого обмоточного провода. После этого магнитопровод с небольшим натягом обматывают фторопластовой лентой. Такая лента под названием ФУМ (фторопластовый уплотнительный материал) продаётся в хозяйственных магазинах. Её необходимо распустить на полоски шириной 4…5 мм и обмотать такой полоской магнитопровод в один слой. Этим достигаются две цели: исключаются меж- витковые замыкания обмотки катушки через магнитопровод и снижается трение провода о него при намотке. При работе с ферритовыми магнитопроводами следует избегать непосредственных ударов по ним и их падений на жёсткие предметы, так как при этом может произойти значительное необратимое изменение начальной магнитной проницаемости материала.
Далее определяют необходимую длину многожильного провода для обмотки. Если известно число витков ка тушки, то рассчитывают число витков провода, разделив первое из этих чисел на число проволок в проводе. Умножив число витков на среднюю длину витка, получаем необходимую длину провода. Среднюю длину витка l я рассчитываю по эмпирической формуле l = D +3h, где D — наружный диаметр магнитопровода; h — его высота. Для ферритового кольца типоразмера К10х6х5 (от дросселя ЭПРА КЛЛ) l = 25 мм. Для катушки, состоящей из 150 витков (коэффициент заполнения окна менее 0,5), потребуется примерно 25х150 = 3750 мм ≈ 3,8 м провода ЛЭШО 7×0,07. Это позволит получить катушку, содержащую 900… 1000 витков провода диаметром 0,07 мм, индуктивностью свыше 1 Гн.
Далее, продев провод через магнитопровод и поместив последний примерно посередине провода, привязываю его одинарным узлом так, чтобы место перекрещивания провода 1 располагалось на наружной цилиндрической поверхности кольца 2 (рис. 1). Концы провода на длине примерно 50 мм и узел промазываю нитроклеем. Минут через пять, после высыхания клея, начинаю наматывать катушку, плотно укладывая витки по внутреннему диаметру кольца. Во избежание расползания витков через каждые два-три витка узел «повторяю», пропуская конец провода внутрь витка. Пройдя первый слой и закрепив конец провода узлом, деревянной зубочисткой устраняю бочкообразность обмотки внутри кольца, поджимая провод к магнитопроводу. Следующий слой наматываю вторым концом провода с небольшим натягом так, чтобы не оборвать проволоки. Жёсткие, пропитанные клеем концы провода облегчают заведение его внутрь кольца. Так, чередуя намотку одним и другим концами провода, заполняю окно, равномерно распределяя обмотку по кольцу. После намотки катушки изготавливаю каркас.
Рис. 1
Для этого в пластине из листового полистирола или другого термопластичного материала толщиной 3…4 мм сверлю отверстие диаметром на 2…3 мм меньше диаметра получившейся катушки. Затем в него ввожу стержень разогретого паяльника мощностью 40…65 Вт и его очищенной от окалины боковой поверхностью разогреваю стенки отверстия. Разогрев веду, непрерывно перемещая стержень паяльника по цилиндрической поверхности отверстия. Оно при этом как бы «развальцовывается», его диаметр увеличивается и на его кромках появляются кольцевые буртики. Развальцевав отверстие до необходимого диаметра, вставляю в него катушку, и пока заготовка не остыла, пинцетом аккуратно обжимаю буртики вокруг катушки. В результате после остывания заготовки она оказывается надёжно зафиксированной в отверстии. Далее заготовку опиливаю до получения необходимой формы каркаса (рис. 2). Излишки провода обрезаю, оставив концы длиной 25…30 мм. Отделив из каждого пучка по одной проволоке, облуживаю их, пользуюсь известным способом — осторожно протягивая проволоку под жалом паяльника с набранным припоем по отрезку поливинилхлоридной изоляции, снятой с монтажного провода. Изоляция проволоки при этом разрушается, и происходит её облуживание. В торцы каркаса 3 вплавляю отрезки лужёного провода диаметром 0,6…0,8 мм — они будут служить выводами 1 катушки 2. Облуженные проволоки наматываю на выводы 1, места намотки пропаиваю.
Рис. 2
Облуживание тонкой проволоки — операция весьма деликатная, велик риск её оборвать, поэтому остальные проволоки я соединяю без снятия изоляции методом сварки. Для этого, взяв по одной проволоке от начала и конца обмотки, скручиваю их на длине примерно 10 мм и нагреваю место скрутки в пламени многоразовой газовой зажигалки с инжекционной горелкой. Пламя такой зажигалки имеет вид узкого конуса голубого цвета. При нагреве проволоки расплавляются, образуя на месте соединения шарик расплавленного металла 4. После остывания место соединения укладываю на каркас так, чтобы проволоки прилегали к каркасу 3, и фиксирую на нём, нагревая жалом остро заточенного паяльника до погружения шарика и проволок в тело каркаса. Так достигается механическая прочность места соединения. После этого скручиваю, свариваю и фиксирую в каркасе вторую пару проволок, затем третью и т. д. В результате все проволоки оказываются соединёнными последовательно, поэтому нет необходимости их «прозвонки». Соединив все проволоки, убеждаюсь в целостности обмотки и отсутствии короткозамкнутых витков в полученной катушке индуктивности, после чего места соединений проволок покрываю клеем БФ-2.
Предлагаемый способ изготовления катушек индуктивности позволяет значительно снизить трудозатраты при их изготовлении. Следует, однако, учесть, что собственная ёмкость намотанной таким способом катушки значительно больше, чем намотанной по обычной технологии внавал.
Автор: К. МОРОЗ, г. Белебей, Башкортостан
Взаимоиндуктивность и ее расчет
Для двух контуров, имеющих w1 и w2 витков с токами I1 и I2 (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф1l—может быть разложен на поток рассеяния Ф1s, пронизывающий только этот контур, и поток взаимоиндукции Ф1m, пронизывающий также и второй контур:
Потокосцепление, соответствующее потоку Ф11 (при условии, что этот поток пронизывает все витки первого контура, равно
а потокосцепление рассеяния
Аналогично для второго контура
Потокосцепление второго контура, определяемое током первого,
а потокосцепление первого контура, определяемое током второго,
Можно показать, что
Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн). Суммарный поток, пронизывающий первый контур,
Суммарное потокосцепление первого контура
и соответственно для второго контура
В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф1м и Ф2м (см. рис. 1.17). Из изложенного видно, что
Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству
а используемый в технических расчетах коэффициент связи двух контуров
Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:
где Lq — индуктивность q-то контура, Мqp = Мрq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет
