Содержание:
Путь и перемещение:
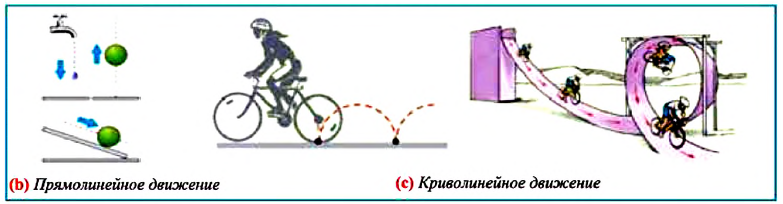
Вы знаете, что любой вид движения совершается по определенной траектории.
Траектория – это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, – криволинейным (с).
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой 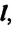
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 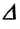 (буква греч. алфавита) перед этой величиной.
(буква греч. алфавита) перед этой величиной.
Изменение координат материальной точки во время движения
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается  то изменение координаты по этой оси будет положительным:
то изменение координаты по этой оси будет положительным: 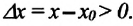 Координата же муравья по оси У уменьшается
Координата же муравья по оси У уменьшается  поэтому изменение его координаты по этой оси будет отрицательным:
поэтому изменение его координаты по этой оси будет отрицательным: 
Изменение радиус-вектора материальной точки во время движения
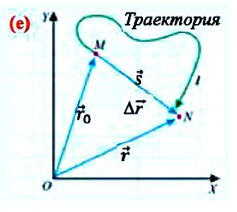
На следующем рисунке представлены радиус-векторы 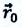 и
и 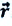 начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор
начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор 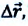 соединяющий концы этих радиус-векторов
соединяющий концы этих радиус-векторов 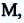 называют перемещением данной материальной точки за промежуток времени
называют перемещением данной материальной точки за промежуток времени 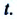 Согласно правилу сложения векторов:
Согласно правилу сложения векторов:  Из последнего выражения получается,
Из последнего выражения получается, 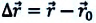 или
или 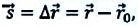 где
где 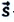 — перемещение материальной точки.
— перемещение материальной точки.
Перемещение – это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.
Векторная величина – это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами – сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
Материальная точка прошла расстояние  от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения:
от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения: 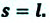

Материальная точка прошла расстояние 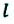 от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку
от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку 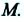 В этом случае материальная точка прошла путь, равный
В этом случае материальная точка прошла путь, равный 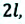 а модуль перемещения равен нулю:
а модуль перемещения равен нулю:

Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение 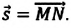 Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения
Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения 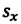 и
и 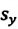 (h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
(h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
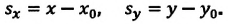
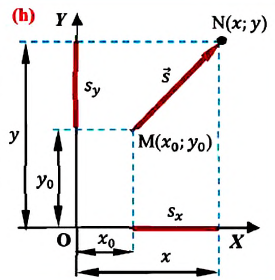
Одинаковы ли путь и перемещение
Задача:
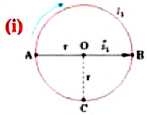
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
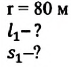
Решение:
Пройденный путь 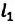 равен длине дуги:
равен длине дуги: 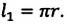
Модуль перемещения же равен диаметру окружности: 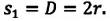
Вычисление:
Что такое путь и перемещение
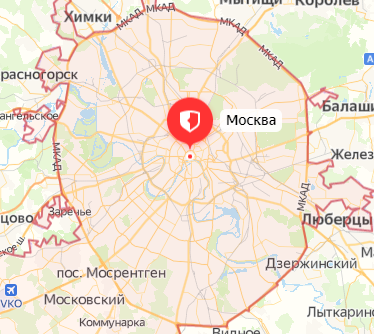
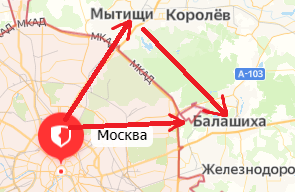
Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь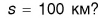
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
Обозначим перемещение символом 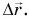 На рисунке 38 вектор
На рисунке 38 вектор 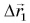 — это перемещение автобуса из Минска в Мытищи, вектор
— это перемещение автобуса из Минска в Мытищи, вектор 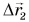 — из Мытищь в Балашиху, а вектор
— из Мытищь в Балашиху, а вектор 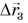 — из Минска в Борисов.
— из Минска в Борисов.
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением 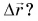 Нельзя, поскольку путь S — скаляр, а перемещение
Нельзя, поскольку путь S — скаляр, а перемещение 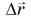 — вектор.
— вектор.
Сравнивать путь S можно с модулем перемещения 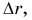 который является скалярной величиной. Равен ли путь модулю перемещения?
который является скалярной величиной. Равен ли путь модулю перемещения?
В рассматриваемом примере путь, пройденный автобусом за два часа, 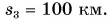 Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова:
Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: 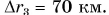 Путь автобуса больше модуля его перемещения:
Путь автобуса больше модуля его перемещения: 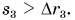
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
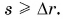
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
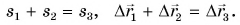
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль 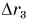 сумме модулей
сумме модулей 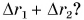 Ответьте самостоятельно.
Ответьте самостоятельно.
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
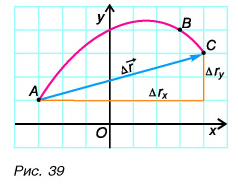
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 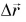 на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
- Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
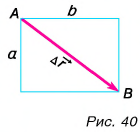

Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
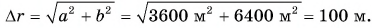
Путь конькобежца: 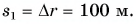
Путь пешехода: 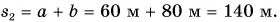
Ответ: 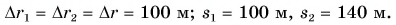
- Заказать решение задач по физике
Траектория движения
Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).

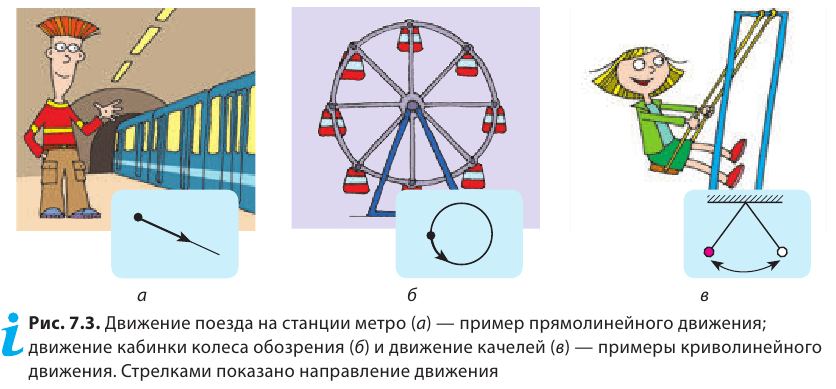
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
Чем путь отличается от перемещения
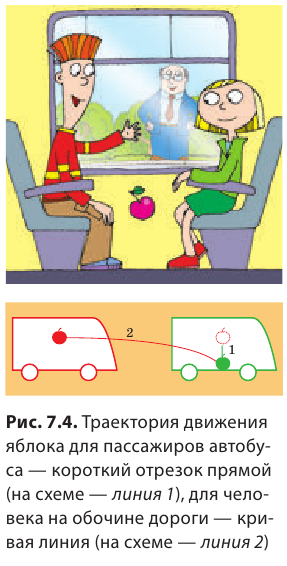
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
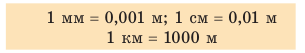
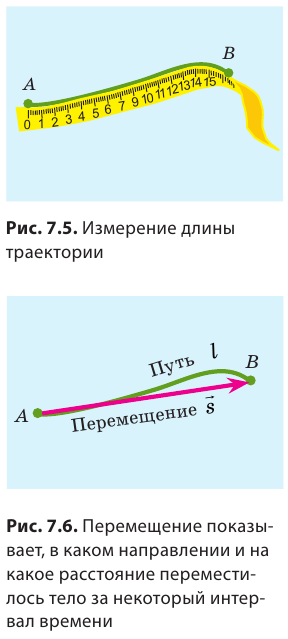
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом 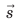 . Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
. Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
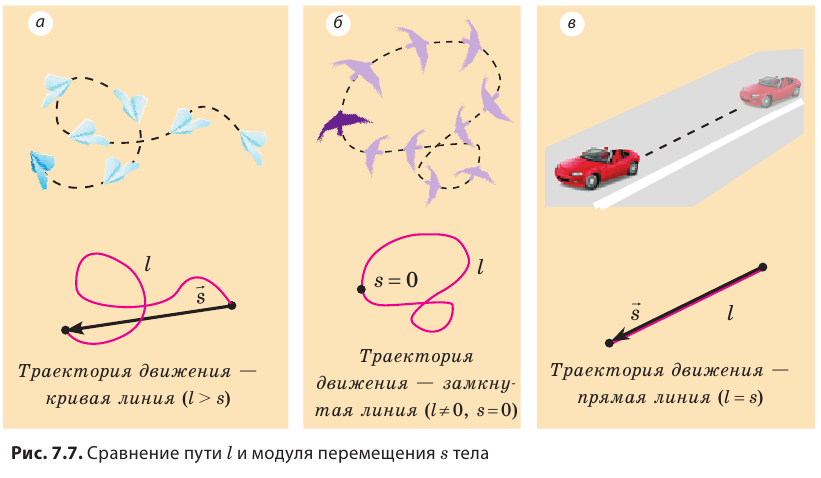
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 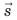 — это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
— это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
Механическое движение.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.
Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.
Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.
Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.
Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат
. Начало координат
является телом отсчёта.
 |
| Рисунок 1. |
Вектор называется радиус-вектором точки
. Координаты
точки
являются в то же время координатами её радиус-вектора
.
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени:
.
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.
К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.
Траектория, путь, перемещение.
В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.
Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора
.
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке
(рис. 2). Тогда путь, пройденный телом, это длина траектории
. Перемещение тела — это вектор
.
 |
| Рисунок 2. |
Скорость и ускорение.
Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).
 |
| Рисунок 3. |
Пусть в момент времени тело находилось в точке
с радиус-вектором
Спустя малый промежуток времени тело оказалось в точке
с
радиус-вектором
Перемещение тела:
(1)
Мгновенная скорость в момент времени
– это предел отношения перемещения
к интервалу времени
, когда величина этого интервала стремится к нулю; иными словами, скорость точки – это производная её радиус-вектора:
(2)
Из (2) и (1) получаем:
Коэффициенты при базисных векторах в пределе дают производные:
(Производная по времени традиционно обозначается точкой над буквой.) Итак,
Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:
Когда стремится к нулю, точка
приближается к точке
и вектор перемещения
разворачивается в направлении касательной. Оказывается, что в пределе вектор
направлен точно по касательной к траектории в точке
. Это и показано на рис. 3.
Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна
, а спустя малый интервал
скорость стала равна
.
Ускорение – это предел отношения изменения скорости
к интервалу
, когда этот интервал стремится к нулю; иначе говоря, ускорение – это производная скорости:
Ускорение, таким образом, есть “cкорость изменения скорости”. Имеем:
Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):
Закон сложения скоростей.
Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим
и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта
, которое движется относительно тела
со скоростью
. Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы
перемещаются параллельно самим себе (нет вращения системы координат), так что вектор
можно считать скоростью движущейся системы относительно неподвижной.
Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью
, это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта
.
Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью
. Муха переносится вагоном, и потому скорость
движущейся системы относительно неподвижной называется переносной скоростью.
Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается
и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе
) обозначается
и называется абсолютной скоростью.
Выясним, как связаны друг с другом эти три скорости – абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
– радиус-вектор точки
в неподвижной системе
;
– радиус-вектор точки
в движущейся системе
;
– радиус-вектор тела отсчёта
в неподвижной системе
.
 |
| Рисунок 4. |
Как видно из рисунка,
Дифференцируя это равенство, получим:
(3)
(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки
в системе
, то есть абсолютная скорость:
.
Аналогично, производная есть скорость точки
в системе
, то есть относительная скорость:
А что такое ? Это скорость точки
в неподвижной системе, то есть – переносная скорость
движущейся системы относительно неподвижной:
В результате из (3) получаем:
Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.
Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!
Виды механического движения.
Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).
Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.
А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.
В терминах вектора скорости можно дать более короткие определения данным типам движения:
Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:
- равноускоренное движение
Наряду с материальной точкой в механике рассматривается ещё одна идеализация – твёрдое тело.
Твёрдое тело – это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.
Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).
 |
| Рисунок 5. |
Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.
На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.
 |
| Рисунок 6. |
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Механическое движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Механическое
движение
–
это изменение положения тел в пространстве
относительно других тел с течением
времени.
Механическое движение может
быть прямолинейным или криволинейным,
равномерным или неравномерным.
Траектория
–
линия, вдоль которой движется
тело.[l]=[м]
По
виду траектории движения разделяются
на прямолинейные и криволинейные.
Путь
– часть длины траектории, вдоль которой
движется тело за время наблюдения, это
скалярная величина (т.е. имеет числовое
значение, но не имеет направления).
[![]()
]=[м]
Перемещение
–
это векторная величина (т.е. имеет модуль
и направление), это направленный отрезок,
соединяющий начало и конец пути.
Система
отсчета
включает в себя 3 понятия:
1.
Тело отсчета – это тело, относительно
которого мы рассматриваем движение.
От выбора тела отсчета зависит: покоится
тело или движется, т.е. механическое
движение понятие относительное.
2.
Систему координат, связанную с телом
отсчета.
3.
Часы – прибор для измерения времени.
2. Равномерное и неравномерное прямолинейное движение. Скорость и ускорение.
Равномерное
прямолинейное движение
– движение, при котором тело за любые
равные промежутки времени совершает
равные перемещения
Оно
характеризуетя:
1.
Постоянной скоростью
![]()
,
[![]()
]=[м/с]
(
=![]()
)
– это векторная величина, показывающая
какое перемещение совершило тело в
единицу времени.
Спидометр
– прибор, для определения скорости.
2.
Траектория
– прямая
1.
для координаты: X
= Xo
+ Vx*t
2.
Vx=const
3.
Sx=X-Xo; Sx = Δx = Vx*t
Неравномерное
прямолинейное движение – движение,
при котором тело за любые равные
промежутки времени совершает разные
перемещения.
Оно
характеризуетя:
1. ≠Const
а)
мг≠const
– скорость в данный момент времени.
б)
ср=const
– отношение всего бути ко всему времени
движения.
ср=
![]()
2.
![]()
=const
– ускорение – физическая векторная
величина, показывающая изменение
скорости в единицу времени. a=
![]()
=[м/с²]
По
проекции скорости говорят о направлении
движения ( Vx>0,
то вдоль OX;
Vx<0,
то против OX)
По
проекции ускорения судят о том ускорено
или замедленно движется тело (Ax>0,
равноускоренное движение; Ax<0,
равнозамедленное движение).
Формулы:
1.
Х=Хo+Vo*t+(Ax*t²)/2
2.
Vx=Vox+Ax*t
3.
Ax=const; Ax=(Vx-Vox)/![]()
4.
Sx=
Vox+(Ax*t²)/2; Sx=(Vx²-Vox²)/2Ax
3. Равномерное движение тела по окружности. Угловая и линейная скорость. Центростремительное ускорение.
Скорость,
с которой тело движется по окружности,
называется линейной
– эта скорость всегда направлена по
касательной к траектории и, хотя числовое
значение у нее не изменяется, направление
в каждой точке меняется.
Изменение
направления скорости приводит к
возникновению центростремительного
ускорения (![]()
).
При
равномерном прямолинейном движении
не возникает ускорение а=0, а при
равноускоренном движении по окружности
всегда возникает.
=V²/R
Чем
больше радиус окружности, по которой
вращается тело, тем меньше
.
Рассмотрим
вращательное движение абсолютно
твердого тела
– тело, где сохраняется расстояние
между частями тела, такое тело имеет
ось вращения. При этом точки оси вращения
покоются, а траектория движения остальных
точек тела – окружность.
Характеристики
вращательного движения:
1.
Период [T]=[c]–
время одного полного оборота. T
показывает число оборотов за время
вращения T=N/t
(N-число
оборотов,t-все
время оборотов). Т-величина обратная
частоте: T=1/ν.
2.
Частота[ν]=[Гц=сˉ¹]
– число оборотов в единицу времени. ν
– величина обратная Т: ν=1/Т=[Гц].
3.
Линейная скорость[
]=[м/с],
![]()
=S/t
4.
Фаза [φ]=[радиан;
С˚] – угол поворота.
5.
Угловая скорость [𝓌]=[радиан/с]
– векторная величина, характеризующая
скорость вращения тела .𝓌=φ/T(для
одного оборота); 𝓌=φ/t(для
нескольких и неполных)
Зависимость
угловой скорости и частоты
𝓌=φ/T=2π/T==(2π/t)/(1/ν)=
2πν
Следовательно,
чем больше радиус окружности, тем
угловая скорость меньше.
Зависимость
линейной и угловой скорости:
V=𝓌R:
V=l/T=2πR/T=(2πR/t)/(1/ν)=
2πRν=
𝓌R
Следовательно,
чем больше радиус окружности, тем
линейная скорость больше.
Вращательное
р/м движение отличается от прямолинейного
р/м движения тем, что при ВРД различные
точки тела движутся с разной скоростью;
при ВРД траектории точек окружности
разных радиусов, а при РПД прямая.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
17.05.2015430.93 Кб221.pdf
- #
- #
Механическое движение. Траектория. Путь. Перемещение

1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).
Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).
Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).
2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.

Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).
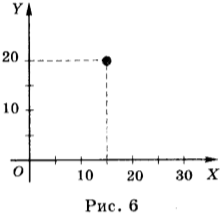
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).
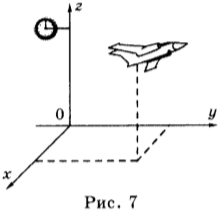
Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.
Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).
3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.
Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.
Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.
Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.
Раздел механики, изучающий способы описания движения тел, называют кинематикой.
4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.
Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.
Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.
Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.
Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.
В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.
Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.
5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.
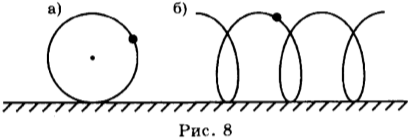
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).
6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.
Если известны траектория тела, его начальное положение и пройденный им путь за время ( t ), то можно найти положение тела в момент времени ( t ). (рис. 9)

Путь обозначают буквой ( l ) (иногда ( s )), основная единица пути 1 м: ( [,mathrm{l},] )= 1 м. Кратная единица пути — километр (1 км = 1000 м); дольные единицы — дециметр (1 дм = 0,1 м), сантиметр (1 см = 0,01 м) и миллиметр (1 мм = 0,001 м).
Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.
7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.
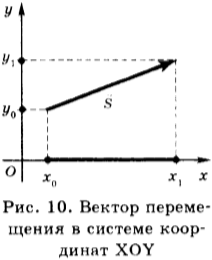
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)
Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается ( overrightarrow{s} ). Единица перемещения ( [,mathrm{s},] ) = 1 м.
Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.
Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.
Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.
При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.
Координаты начала перемещения — ( x_0, y_0 ); координаты конца перемещения — ( x_1, y_1 ). Проекция вектора перемещения на ось ОХ равна: ( s_x=x_1-x_0 ). Проекция вектора перемещения на ось OY равна: ( s_y=y_1-y_0 ).
Модуль вектора перемещения равен: ( s=sqrt{s^2_x-s^2_y} ).
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В состав системы отсчёта входят
1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы
2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно
1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора
4. Относительно какого тела покоится автомобиль, движущийся по автостраде?
1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода
5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с
6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с
7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?
1) прямая
2) окружность
3) дуга
4) винтовая линия
8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь ( l ) и модуль перемещения ( s ) мяча за всё время движения?
1) ( l )= 3,3 м, ( s ) = 3,3 м
2) ( l ) = 3,3 м, ( s ) = 0,7 м
3) ( l )= 0,7 м, ( s ) = 0,7 м
4) ( l )= 0,7 м, ( s ) = 3,3 м
9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?
1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй
10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса ( R ). Чему равны при этом путь ( l ) и модуль перемещения ( s ) точки обода?
1)( l=2R ), ( s=2R )
2)( l=pi R ),( s=2R )
3)( l=2R ),( s=pi R )
4) ( l=pi R ), ( s=pi R ).
11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор
ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта
12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения
ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная
Часть 2
13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.
Ответы
Механическое движение. Траектория. Путь. Перемещение
2.9 (57.28%) 213 votes
Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.
Виды движений тела
Существуют несколько видов движений и траекторий твердого тела:
- поступательное;
- вращательное, то есть движение по окружности;
- плоское, то есть перемещение по плоскости;
- сферическое, характеризующее движение по поверхности сферы;
- свободное, иначе говоря, произвольное.
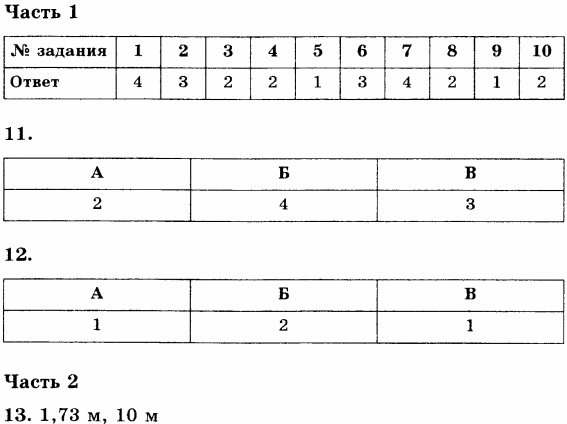
Рисунок 1. Определение точки при помощи координат x=x(t), y=y(t), z=z(t) и радиус-вектора r→(t), r0→ является радиус-вектором точки в начальный момент времени
Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x=x(t), y=y(t), z=z(t) или от времени радиус-вектора r→=r→(t), проведенного из начала координат к заданной точке. Это показано на рисунке 1.
Перемещение тела
Перемещение тела s→=∆r12→=r2→-r1→ – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t.
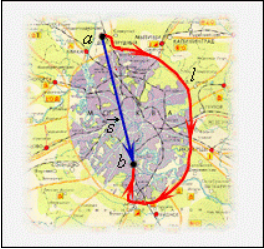
Рисунок 2. Пройденный путь l и вектор перемещения s→ при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Перемещение принято считать векторной величиной. Этот отрезок имеет направление.
Путь – скалярная величина. Считается числом.
Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3, как показано на рисунке 3.
Рисунок 3. Сумма двух последовательных перемещений ∆r→13=∆r→12+∆r→23=r→2-r→1+r→3-r→2=r→3-r→1
Когда радиус-вектор материальной точки в определенный момент времени t является r→(t), в момент t+∆t есть r→(t+∆t), тогда ее перемещение ∆r→ за время ∆t равняется ∆r→=r→(t+∆t)-r→(t).
Перемещение ∆r→ считается функцией времени t: ∆r→=∆r→(t).
По условию дан движущийся самолет, представленный на рисунке 4. Определить вид траектории точки М.
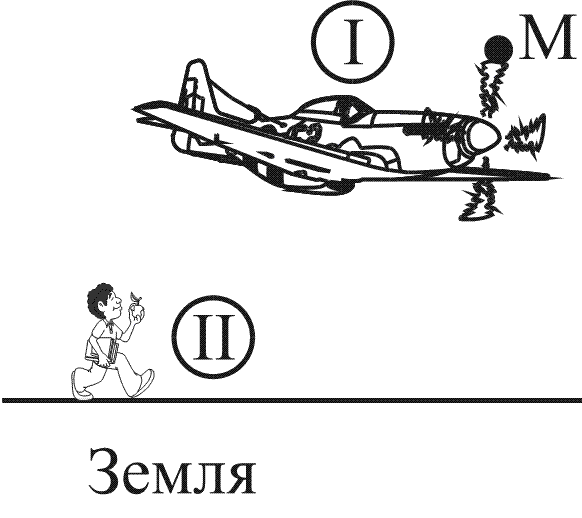
Рисунок 4
Решение
Необходимо рассмотреть систему отсчета I, называемую «Самолет» с траекторией движения точки М виде окружности.
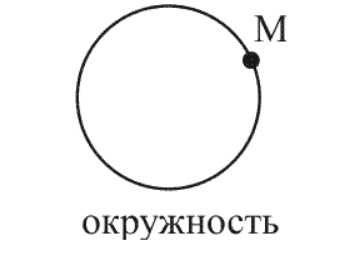
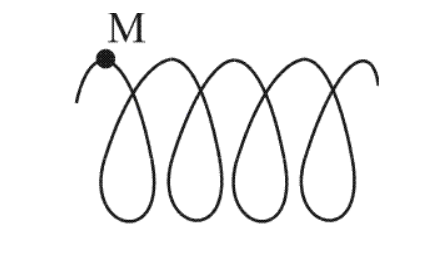
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.
Дана материальная точка, которая совершает движение из А в В. Значение радиуса окружности R=1 м. Произвести нахождение S, ∆r→.
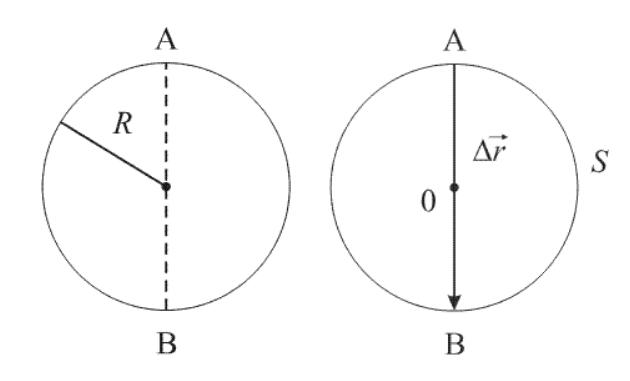
Решение
Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:
S=πR.
Подставляем числовые значения и получаем:
S=3,14·1 м=3,14 м.
Перемещением ∆r→ в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В.
Подставив числовые значения, вычислим:
∆r→=2R=2·1=2 м.
Ответ: S=3,14 м; ∆r→=2 м.
