Треугольнике в физике как найти

Центр тяжести в физике – формулы и определение с примерами

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.

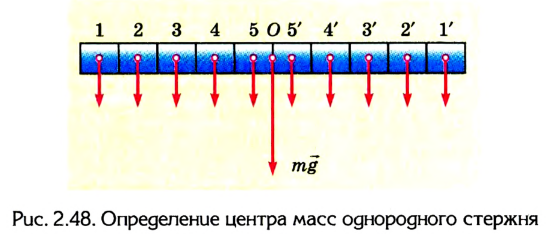
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

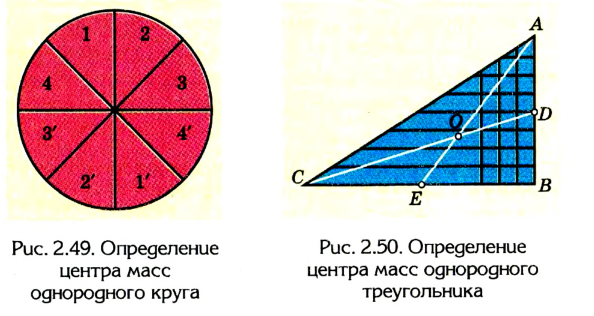
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

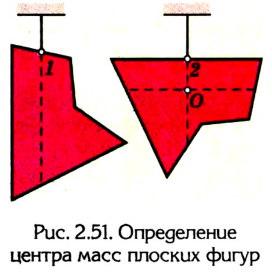
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

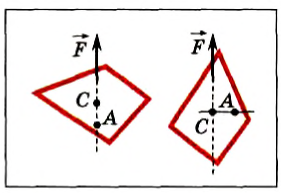
Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

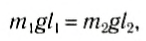
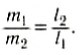
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид: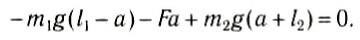

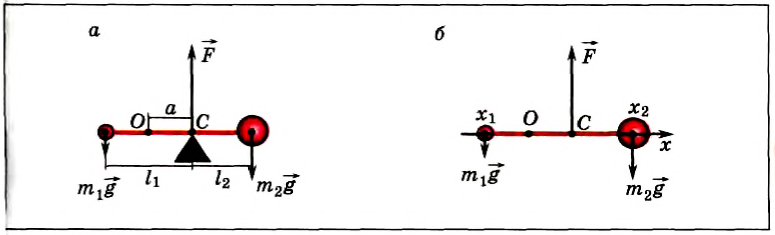
Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

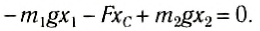
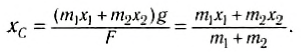
При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂. m_n, и если известны координаты центров масс этих элементов x₁, x₂. x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

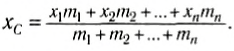
Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =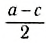, а координаты центра масс линейки: 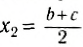, y₂ = 0 .
По формуле (3): .

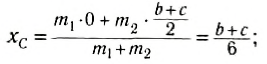
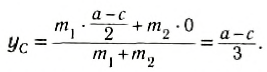
Таким образом, центр масс угольника находится вне тела.

Главные выводы:

1. Центр тяжести — точка, в которой приложена сила тяжести.
2. Центр масс симметричных однородных тел находится в их геометрическом центре.
3. Координаты центра масс тела можно вычислить по формуле (3).

• Импульс тела в физике
• Замкнутая система в физике
• Реактивное движение в физике
• Освоение космоса – история, этапы и достижения с фотографиями
• Международная система единиц СИ
• Математика – язык физики
• Законы Ньютона в физике
• Гравитационные силы в физике

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Дельта — буква, знак и его происхождение, применение в науке

В данной статье поговорим о знаке Дельта – что он из себя представляет, в каких сферах применяется и для чего вообще используется. Также вы узнаете, как выглядит знак и как его можно вставить в текст в такой программе, какой является Ворд из Майкрософт Оффис.

Знак Дельта применяется во многих сферах жизнедеятельности, к примеру, в физике, текстовых редакторах, формулах и других сферах. Чаще всего именно при печати учебной литературы, докладов и других видов документов применяют знак дельта, который имеется в разных версиях ВОРД от Виндовс и других приложениях для создания документов текстового формата на ПК.

О происхождения знака

Появление символа связано с греческими языком, но сама буква появилась от стародревнего финийского языка, в котором именовалась – далет, что обозначало («вход в дверь»). Выглядела «далет» как перевернутый влево равнобедренный треугольник. В греческом алфавите, была такая буква. Позже эта буква дала начало всем известной буквы латинского набора – D , которая и поныне есть во многих алфавитных рядах разных государств мира, к примеру, английский алфавит ее содержит.

Буква, которая служит аналогом в русском алфавите – Д, а вот символ везде одинаков и изображается, как геометрическая фигура, а именно треугольник с равными сторонами (Δ). Эта версия является заглавной, прописная версия выглядит немного иначе, представляя собой кружок с хвостиком, похожий на обозначение в физике плотности (δ).

Где применяется данный символ?

Кроме использования в правописании греков, символ начали активно применять в математике, геометрии, алгебре, физике, химии и географии.

Поговорим отдельно о применении дельта в каждых научных сферах:

1. География. Дельта подразумевает в географическом смысле начальную часть реки, океана или моря, имеет смысловое, нежели символическое, буквенное понятие и восприятие. Почему именно область впадения реки принято так называть? Все просто, дело в форме данной области, если сделать снимок сверху, то отток реки будет иметь форму правильного треугольника, а символ дельта, как раз представляет собой такой геометрический объект. Ярчайшим представителем с выраженной дельтой является река Нил (Египет), которая впадает в Средиземное море, а также Амазонка с ее впадением в океан Атлантики.
2. Применение в математике, алгебре, геометрии. Очень часто знак применяют в математической сфере для таких целей, как: 1) Приращение аргумента подразумевает под дельтой измененную переменную. К примеру, сложим 5 и 4 в итоге получим число 9. Дельтой будет являться увеличение 5 на 4. 2) Применение в теории вероятности по системе Лапласа. Такой метод преподают в ВУЗах, а не школах и в нем используют такой знак. 3) А также символ применяется при обозначении прямой и обратной матриц. 4) Дельта, буква, применяемая в написании формул (как письменным методом, так и через компьютер);
3. Также в математике применяют прописную версию дельта. А именно, такой символ обозначает производную от числа. Обозначение выглядит следующим образом – δy/δx. 2) Используется для описания бесконечной функции-дельта. Бесконечная функция возможна, если все значения аргумента равны нулю. 3) При помощи δ еще обозначают символику Кронекера, символ равен всегда 1, при условии того, что все его индексы равны, либо нулевые при заданных условиях.
4. Физика, астрономия, космогония. Граничащие меж собой научные дисциплины, все особо важные и по-своему интересные, в каждой из дисциплин можно встретить знак дельта. В физике связь всех производных осуществляется при помощи формул с интеграцией. К примеру, формула скорости, которая выглядит следующим образом – δS к δt , является отношением одной части к другой. В данном случае расстояние, которое преодолел объект, соотносится со временем, затраченном на преодоление. Вторая производная – это ускорение, где тоже важна взаимосвязь одной составляющей формулы к другой. В космологии и астрономии применяют формулы, расчеты с данным символом, только в прописном варианте.

Как ввести в «Ворд»?

Для вставки символа заходим в верхние меню редактора и ищем колонку «Вставка», наводим на колонку курсором мыши без нажатия правой кнопки. Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».

Треугольник мощностей

Треугольник мощностей представляет собой прямоугольный треугольник, показывающий соотношение между активной, реактивной и полной мощностью.

Когда каждая составляющая тока (активная составляющая (Icosϕ) или реактивная составляющая (Isinϕ)) умножается на напряжение U, получается треугольник мощности, показанный на рисунке ниже:

Мощность, которая фактически потребляется или используется в цепи переменного тока, называется активной мощностью или реальной мощностью. Она измеряется в ваттах (Вт), киловаттах (кВт) или МВт.

Мощность, которая протекает в линиях переменного тока, но не выполняет полезной работы, называется реактивной мощностью. Реактивная мощность измеряется в вольт-амперах (ВАр) реактивных, киловольт-амперах реактивных (кВАр) или МВАр.

Произведение среднеквадратичного значения напряжения и тока известно как полная мощность. Она измеряется в вольт-амперах (ВА), кВА или МВА.

Следующий пункт показывает взаимосвязь между электрическими величинами и объясняется графическим представлением под названием треугольник мощностей, показанным выше.

• Когда активная составляющая тока умножается на напряжение цепи U, получается активная мощность. Именно она создает крутящий момент в двигателе, нагревает резистор и выполняет другую полезную работу. Она измеряется ваттметром.
• Когда реактивная составляющая тока умножается на напряжение цепи, получается реактивная мощность. Она определяет коэффициент мощности сети. Она не выполняет полезную работу, а только перегоняется по сети, создавая препятствия для полезной мощности.
• Когда общий ток цепи (активный и реактивный) умножается на напряжение — мы получаем полную мощность.

Коэффициент мощности (cos φ) может быть определен из треугольника мощностей путем вычисления отношений активной мощности к полной:

Как мы знаем, обычная мощность означает произведение напряжения и тока, но в цепи переменного тока, за исключением чисто резистивной нагрузки, обычно существует разность фаз между напряжением и током, и поэтому произведение напряжения и тока не отражает реальной или активной мощности в цепи.

[spoiler title=”источники:”]

http://liveposts.ru/articles/education-articles/delta-bukva-znak-i-ego-proishozhdenie-primenenie-v-nauke

http://elenergi.ru/chto-takoe-treugolnik-moshhnostej-i-kakovo-ego-naznachenie.html

[/spoiler]

Неотъемлемой частью изучения физики является решение задач. Решение любой расчётной задачи связано с формулами, поэтому надо уметь их преобразовывать. В методике преподавания физики есть инструмент называемый «треугольник формул». Он необходим для запоминания трех различных, но взаимосвязанных формул. Рассмотрим самую первую взаимосвязь трех физических величин, которые на уроках математики мы почти наизусть выучили: скорость, путь, время. Достаточно помнить лишь основную формулу и воспользоваться треугольником-помощником для её преобразования.

Слева – исходная формула, а справа – помощник-треугольник:	Знаем, что
	=>
Как пользоваться треугольником?
	=>		скорость определяется отношением пройденного пути ко времени движения.
Как выразить путь?
	=>		пройденный путь равен произведению скорости на время.
Как выразить время?
	=>		для нахождения времени надо путь разделить на скорость.

Таким образом, один треугольник вместил в себя сразу три формулы. Такой метод запоминания подойдёт и для любых других похожих формул, только нужно вписать нужные величины.

Треугольник формул	Знаем, что
	=>
Как определить плотность тела?
	=>		плотность вещества определяется отношением массы к объему тела.
Как найти массу?
	=>		масса равна произведению плотности на объем.
Как вычислить объем?
	=>		для нахождения объема тела надо массу разделить на плотность вещества.

Теперь рассмотрим физическую задачу, в которой могут быть использованы знания свойств треугольника.

Задача (ЕГЭ, 2016): Точечное тело массой 2 кг свободно движется по горизонтальному столу вдоль оси ОХ с постоянной скоростью, модуль которого равен 4м/с. В некоторый момент времени на это тело начинает действовать сила 8Н, направленная вдоль стола в положительном направление ОУ. Чему равен импульс тела через одну секунду после действия силы?

Решение: Величина импульса, направленного вдоль оси ОХ равна . Величина импульса, направленного вдоль оси ОУ равна . Построим чертеж:

Равнодействующий импульс направлен по биссектрисе прямого угла равнобедренного треугольника. Значит значение его будет .

Ответ: .

Подобие треугольников, в частности подобие прямоугольных треугольников, моделирует правило рычага. Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.

Правило рычага гласит: Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам: . Геометрическое объяснение описываемого явления легко заметить из подобия треугольников AOF₁ и AOF₂.

Задача (ЕГЭ 2015): Рычаг изготовлен из легкой доски. Где должна быть точка опоры, чтобы рычаг находился в равновесии?

Решение: Имеем следующие данные: F₁=300Н, F₂=200Н. Вспомним правило рычага: . Значит, первое плечо l1 составляет 1/3 длины рычага, второе плечо l2 составляет 2/3 длины рычага.

Равенство углов, сумма углов треугольника, подобие треугольников находят применение при решение задач по оптике.

Например:Известно, что луч света параллельный главной оптической оси линзы, пройдя через линзу, изменяет свое направление так, что его действительное или воображаемое продолжение проходит через главный фокус; луч, проходящий через оптический центр линзы, направления не изменяет. Построив изображение описываемого процесса, мы видим, что линейное увеличение линзы (отношение линейного размера изображения к линейному размеру предмета)равно отношению расстояния от линзы до изображенияfк расстоянию от линзы до предмета.

Рассмотрим несколько примеров таких задач с использованием теоремы Пифагора для решения. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой.

1. При строительстве в зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.
2. Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты.

Задача: Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

Решение: По теореме Пифагора h₂ ≥ a₂+b₂, значит h ≥ (a₂+b₂)½.

1. При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки.

Задача: В доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.

Решение: Треугольник ADC – равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда из треугольника DBC: DB=2,5 м., 

Ответ: 5,7 метров.

1. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать типичную задачу.

Задача: Какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, в радиусе R=200 км, если известно, что радиус Земли равен 6380 км.)

Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км. OB = OA + AB.

OB = r + x . Используя теорему Пифагора, получим ответ.

Ответ: 2,3 км.

Задача: 12 апреля 1961 года Ю.А. Гагарин на космическом корабле «Восток» был поднят над землёй на максимальную высоту 327 километров. На каком расстоянии от корабля находились в это время наиболее удалённые от него и видимые космонавтом участки поверхности Земли? (Радиус Земли ≈6400 км).

Решение: Точка А – место расположения космического корабля. Точка В – видимый космонавтом участок поверхности Земли. Точка О – центр Земли. Так как АВ – касательная к окружности, а ОВ – радиус, то получаем, что треугольник АВО – прямоугольный с прямым углом В. ОВ=6380. ОА=327+6380=6707. По теореме Пифагора катет АВ=2069км.

Задача индийского математика XII века Бхаскары.

«На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в этом месте река

В четыре лишь фута была широка

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?»

Решение: По теореме Пифагора . Высота тополя равна DC = DB + BC = 5 + 3 = 8м

Задача из учебника «Арифметика» Леонтия Магницкого

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти нужно.»

Решение: По теореме Пифагора  стоп.

Задача из китайской «Математики в девяти книгах»: Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?

Решение: x – глубина водоема, x+1 – длина камыша. По теореме Пифагора составим уравнение . Решив это уравнение, получаем значение x=12.

Ответ: глубина озера составляет 12 метров, длина камыша – 13 метров.

Такие задачи описаны в различных книгах, которые показывают нам историческую значимость теоремы Пифагора. В дополнение предлагаем решить некоторые задачи из области физики, которые с легкостью можно решить на уроке геометрии. На уроках по физике ученики сталкиваются с теоремой Пифагора чаще всего при изучении механических и оптических явлений.

Задача: Какую скорость относительно воды должен сообщить мотор катеру, чтобы при скорости течения реки, равной 2 м/с, катер двигался перпендикулярно к берегу со скоростью 3,5 м/с относительно берега?

Решение:

По теореме Пифагора получаем

Ответ: скорость лодки должна быть равной 4,03 м/с.

Задача: Мяч брошен под углом 450 к горизонту со скоростью 20 м/с с поверхности Земли. Найдите высоту подъема мяча через 2 секунды.

Решение:

Задача 3: Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

Решение:

Длина троса является гипотенузой прямоугольного треугольника. По теореме Пифагора получаем . Устанавливают 4 троса. 4·13=52м.

Ответ: 50 метров троса не хватит, нужно еще 2 метра.

Стороны прямоугольного треугольника могут превратиться в линейный сегмент любой фигуры, и стать переменными в любом квадратном уравнении. Например, в задаче по физике можно в формулу расчёта кинетической энергии  объекта массой m при скорости v применяем теорему Пифагора и получаем следующее. Энергия при скорости в 500 км/ч равна сумме энергий при скорости в 400 км/ч и при скорости в 300 км/ч. Значит, одного и того же количества энергии хватает либо на запуск одного предмета на скорости 500 км/ч, либо на запуск двух других на меньшей скорости.

Решим физическую задачу, пользуясь только геометрическими соображениями.

Задача: Фонарь подвешен на двух равных по длине тросах. Вес фонаря равен 10 Н. Определите силу натяжения каждого из тросов.

В треугольнике АВС по теореме Пифагора найдем длину троса АВ:  Пусть вся сила натяжения троса F направлена по вектору ВА. Имеем пропорциональное соотношение:  Так как фонарик подвесили на два троса, то сила натяжения одного торса равна 50,2 Н.

Ответ: 50,2 Н.

Список литературы:

1. Ковтунович М. Г. – Домашний эксперимент по физике. 7-11 классы (Библиотека учителя физики) – 2007
2. Робертсон Б. Современная физика в прикладных науках. М., 1985.
3. Энциклопедия для детей. Математика. Том 11. – М.: Аванта+, 2001, с. 381

Обозначения:

А, В, С — вершины, а также углы при этих вершинах;

а, b, с — стороны, противолежащие углам
А, В, С соответственно;

ha, hb, hc — высоты, опущенные на стороны

а, b, с соответственно;

ma, mb, mc — медианы;

la, lb, lc — биссектрисы;

R — радиус описанной окружности;

r — радиус вписанной окружности.

треугольник

Подобие треугольников
Признак 1

Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника.

Признак 2

Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого и углы, образованные этими сторонами в этих треугольниках, равны.

Признак 3

Два треугольника подобны, если три стороны одного треугольника пропорциональны сторонам другого треугольника.

Прямоугольные треугольники подобны,
если гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.

подобие треугольников

Если треугольники подобны, то

Пропорциональные отрезки в треугольнике

Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:

Высотой треугольника
называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.

Высоты треугольника пересекаются в одной точке О, называемой ортоцентром.

В тупоугольном треугольнике ортоцентр лежит вне треугольника.
В прямоугольном он совпадает с вершиной прямого угла.

высоты треугольника

Медианой треугольника
называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.

Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника.

Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины) .

медианы треугольника

Биссектрисой треугольника
называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной.

Биссектрисой угла называется луч, делящий угол пополам.

Биссектрисы треугольника пересекаются в одной точке, являющейся центром впмсанной окружности.

биссектрисы треугольника

Равенство треугольников
Признак 1

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Признак 2

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Признак 3

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

равенство треугольников

Два треугольника называются равными, если при наложении друг на друга они совместятся.
Если
то соответственные стороны
равны

и соответственные углы равны

Неавенства треугольника
Всякая сторона треугольника меньше суммы и больше разности двух сторон

Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Площадь треугольника

где р — полупериметр треугольника (формула Герона) .