Тупоугольный треугольник как найти биссектрису - Сайт, где вы сможете решить свои вопросы

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

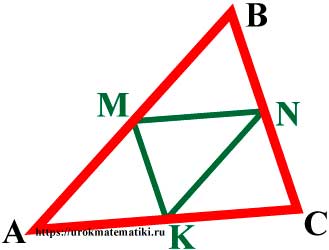
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Все формулы биссектрисы в треугольнике

L – биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

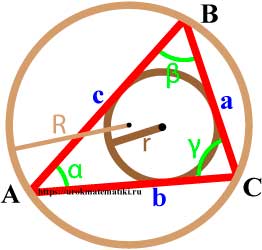
γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

Элементы треугольника. Высоты, медианы, биссектрисы

Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.

Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.

Попробуйте провести три высоты в тупоугольном треугольнике. Получилось? Да, редкий выпускник справляется с этим заданием. Действительно, мы не можем опустить перпендикуляр из точки на отрезок , зато можем опустить его на прямую — то есть на продолжение стороны .

В этом случае в одной точке пересекаются не сами высоты, а их продолжения.

А как выглядят три высоты в прямоугольном треугольнике? В какой точке они пересекаются?

Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.

Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении , считая от вершины.

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла. Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника. Эта точка является центром окружности, вписанной в треугольник.

Еще одно свойство биссектрисы пригодится тем, кто собирается решать задачу . Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.

Ты нашел то, что искал? Поделись с друзьями!

Разберем несколько задач, в которых речь идет о высотах, медианах и биссектрисах треугольника. Все задачи взяты из Банка заданий ФИПИ.

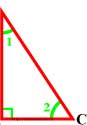
1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

Пусть биссектрисы треугольника (в котором угол равен ) пересекаются в точке .

Острый угол между биссектрисами на рисунке обозначен .

Угол смежный с углом , следовательно, .

Поскольку треугольник — прямоугольный, то .

2. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Пусть — высота, проведенная из вершины прямого угла , — биссектриса угла .

Угол между высотой и биссектрисой — это угол .

3. Два угла треугольника равны и . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

Из треугольника (угол — прямой) найдем угол . Он равен .

Из треугольника ( — прямой) найдем угол . Он равен .

В треугольнике известны два угла. Найдем третий, то есть угол , который и является тупым углом между высотами треугольника :

4. В треугольнике угол равен , и — биссектрисы, пересекающиеся в точке . Найдите угол . Ответ дайте в градусах.

Пусть в треугольнике угол равен , угол равен .

Из треугольника получим, что .

5. В треугольнике угол равен , угол равен . , и — биссектрисы, пересекающиеся в точке . Найдите угол . Ответ дайте в градусах.

Найдем угол . Он равен .

Из треугольника найдем угол . Он равен .

6. В треугольнике , — медиана, угол равен , угол равен . Найдите угол . Ответ дайте в градусах.

Как решать эту задачу? У медианы прямоугольного треугольника, проведенной из вершины прямого угла, есть особое свойство. Мы докажем его в теме «Прямоугольник и его свойства».

Подсказка: Сделайте чертеж, найдите на нем равнобедренные треугольники и докажите, что они равнобедренные.

[spoiler title=”источники:”]

http://www-formula.ru/bisectortriangle

http://ege-study.ru/ru/ege/materialy/matematika/vysota/

[/spoiler]

Источник

Тупоугольный треугольник, элементы, свойства, признаки и формулы.

Тупоугольный треугольник – это треугольник, у которого один угол тупой.

Тупоугольный треугольник (понятие и определение)

Элементы тупоугольного треугольника

Свойства тупоугольного треугольника

Формулы тупоугольного треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Тупоугольный треугольник (понятие и определение):

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов

Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

∠ АВС, ∠ BСA – острые углы треугольника

По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник, т.к. у него каждый угол составляет 60°.

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.

Рис. 3. Прямоугольный треугольник

Тупоугольный треугольник также может быть одновременно равнобедренным треугольником. Но не всякий равнобедренный треугольник тупой.

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

∠ ВАС – вершинный угол, ∠ АBC и ∠ BСA – углы при основании

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

АВ = АС

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:

- a < b + c;
- a > b – c;
- b < a + c,
- b > a – c;
- c < a + b;
- c > a – b.

Квадрат

Овал

Остроугольный треугольник

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Тупоугольный треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
20 488

Источник

L– биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p=(a+b+c)/2

Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

Подробности

Опубликовано: 06 октября 2011

Обновлено: 13 августа 2021

Источник

Треугольник

Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

типы треугольников
вершины углы и стороны треугольника
медианы треугольника
биссектрисы треугольника
высоты треугольника
окружность вписанная в треугольник
окружность описанная вокруг треугольника
связь между вписанной и описанной окружностями треугольника
средняя линия треугольника
периметр треугольника
формулы площади треугольника
равенство треугольников
подобие треугольников
прямоугольные треугольники

Типы треугольников

По величине углов

Остроугольный треугольник

— все углы треугольника острые.

Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).

Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).

По числу равных сторон

Разносторонний треугольник

— все три стороны не равны.

Равнобедренный треугольник

— две стороны равны.

Равносторонний (правильный) треугольник

— все три стороны равны.

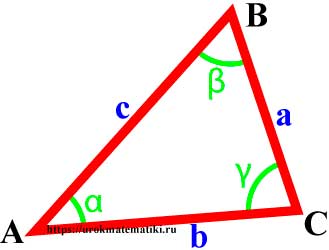
Вершины, углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

α + β + γ = 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

если α > β, тогда a > b
если α = β, тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

asinα = bsinβ = csinγ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

a2 = b2 + c2 – 2bc·cos α
b2 = a2 + c2 – 2ac·cos β
c2 = a2 + b2 – 2ab·cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 232mb2+mc2-ma2b = 232ma2+mc2-mb2c = 232ma2+mb2-mc2

Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника

Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD=
BOOE=COOF=21
Медиана треугольника делит треугольник на две равновеликие частиS∆ABD=S∆ACDS∆BEA=S∆BECS∆CBF=S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольниковS∆AOF=S∆AOE=S∆BOF=S∆BOD=S∆COD=S∆COE
Из векторов, образующих медианы, можно составить треугольник

Формулы медиан треугольника

Формулы медиан треугольника через стороны

ma = 122b2+2c2-a2mb = 122a2+2c2-b2mc = 122a2+2b2-c2

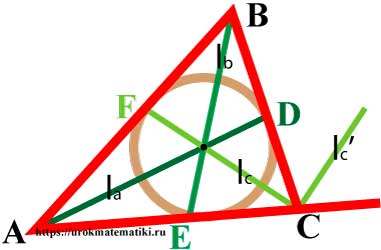
Биссектрисы треугольника

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника

Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, – центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB=
ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
Угол между

lc и lc’ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

la = 2bcpp-ab+clb = 2acpp-ba+clc = 2abpp-ca+b

где p = a+b+c2 — полупериметр треугольника.

Формулы биссектрис треугольника через две стороны и угол

la = 2bc cosα2b+clb = 2ac cosβ2a+clc = 2ab cosγ2a+b

Высоты треугольника

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться:

внутри треугольника — для остроугольного треугольника;
совпадать с его стороной — для катета прямоугольного треугольника;
проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc=1a:1b:1c=
BC:AC:AB
1ha:1hb:1hc=1r

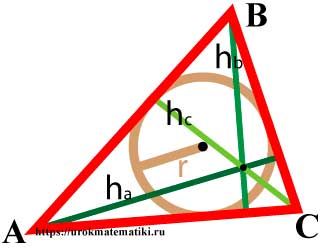
Формулы высот треугольника

Формулы высот треугольника через сторону и угол

ha = b sin γ = c sin βhb = c sin α = a sin γhc = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

ha = 2Sahb = 2Sbhc = 2Sc

Формулы высот треугольника через две стороны и радиус описанной окружности

ha = bc2Rhb = ac2Rhc = ab2R

Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

r = Sp

Радиус вписанной в треугольник окружности через три стороны

r = a+b-cb+c-ac+a-b4a+b+c

Формулы высот треугольника через две стороны и радиус описанной окружности

1r=1ha+1hb+1hc

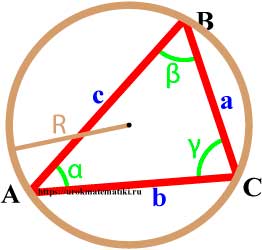
Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

R = abc4S

Радиус описанной окружности через площадь и три угла

R = S2 sinα sinβ sinγ

Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

R =a2 sinα+b2 sinβ+c2 sinγ

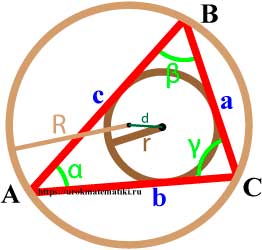
Связь между вписанной и описанной окружностями треугольника

Формулы радиуса окружности описанной вокруг треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то

d2 = R2 – 2Rr

Радиус описанной окружности через площадь и три угла

rR = 4sinα2 sinβ2 sinγ2 = cosα + cosβ + cosγ

2Rr =abca+b+c

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника

Любой треугольник имеет три средних линии.
Средняя линия треугольника параллельна основанию и равна его половине.
MN= 12AC; KN= 12AB; KM= 12BCMN || AC; KN || AB; KM || BC
Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника.
S∆MBN = 14S∆ABC; S∆MAK = 14S∆ABC;
S∆NCK = 14S∆ABC
При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN ~ ∆ABC;
∆AMK ~ ∆ABC;
∆KNC ~ ∆ABC;
∆NKM ~ ∆ABC

Признаки

Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон.

P = a + b + c

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

S = 12 a · ha

S = 12 b · hb

S = 12 c · hc

где a, b, c — стороны треугольника,
h_a, h_b, h_c — высоты, проведенные к сторонам a, b, c треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.

S = pp-ap-bp-c

где p — полупериметр треугольника: p = a + b + c2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 12 a · b · sinγ

S = 12 b · c · sinα

S = 12 a · c · sinβ

где a, b, c — стороны треугольника,
γ — угол между сторонами a и b,
α — угол между сторонами b и c,
β — угол между сторонами a и c.

Формула площади треугольника по трем сторонам и радиусу описанной окружности

S = a · b · c4R

a, b, c — стороны треугольника,
R – радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

S = p · r

где S — площадь треугольника,
r – радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c2

Равенство треугольников

Определение

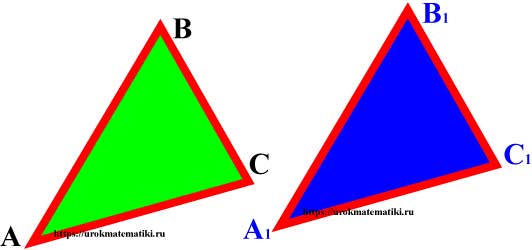
Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Теорема.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Теорема.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Теорема.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

Определение

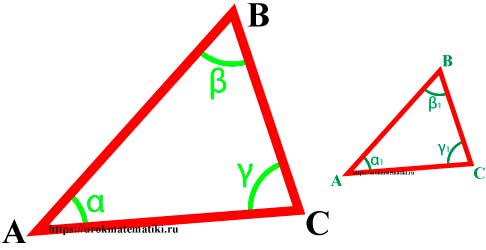
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

∆АВС~∆MNK=> α=α1

β=β1

γ=γ1

ABMN=BCNK=ACMK=k

где k — коэффициент подобия.

Признаки подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

S∆АВСS∆MNK=k2

Прямоугольные треугольники

Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).

Свойства прямоугольного треугольника

Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1+∠ 2=90°.
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

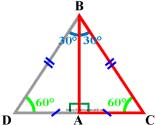
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.

Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

S∆АВСS∆MNK=k2

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Источник

Биссектриса треугольника – это отрезок, делящий любой угол треугольника на два равных угла. Для более
наглядного примера, если угол равняется 120°, то проведенная биссектриса создает уже пару углов по
60 °. В треугольнике можно провести максимум три биссектрисы, по одной из каждого угла. Точка
пересечения всех биссектрис является центром вписанной в треугольник окружности. Биссектриса
обладает особенными свойствами для некоторых видов треугольников, так, например, проведенная из
вершины равнобедренного треугольника будет являться одновременно и высотой, и медианой.

Длина биссектрисы в треугольнике через две стороны и угол
между ними
Длина биссектрисы в треугольнике через все стороны
Длина биссектрисы в треугольнике через две стороны и
отрезки
Длина биссектрисы в прямоугольном треугольнике через
катеты
Длина биссектрисы в прямоугольном треугольнике через
гипотенузу и угол
Длина биссектрисы из острого угла в прямоугольном
треугольнике через катет и угол
Длина биссектрисы из острого угла в прямоугольном
треугольнике через катет и гипотенузу
Длина биссектрисы в равнобедренном треугольнике через
боковую сторону и угол при основании
Длина биссектрисы в равнобедренном треугольнике через
основание и угол при основании
Длина биссектрисы в равнобедренном треугольнике через
боковую сторону и угол между боковыми сторонами
Длина биссектрисы в равнобедренном треугольнике через
основание и боковую сторону
Длина биссектрисы в равностороннем треугольнике через
сторону

Через две стороны и угол между ними

Нам дан некий треугольник, известно значение двух сторон и угла между ними. Нам нужно найти
биссектрису. Задача кажется невыполнимой, если не знать формулы:

L = (2bc · cos (α/2)) / b + c

где «L» это непосредственно длина, а «b» и «с» — стороны треугольника, «α» — угол между
ними.

Цифр после
запятой:

Результат в:

В нашем случае биссектриса равняется среднему двух сторон и угла, лежащего между ними.

Пример. Дан треугольник ABC. Известно, что стороны b = 6 см, а сторона c = 9 см.
Угол между двумя сторонами равен 65°. Нам нужно найти биссектрису. Подставив в формулу данные
значения, мы получаем ответ – биссектриса треугольника АВС равна 6 см. Решение легкое, ведь вам
нужно прибегнуть к обычному применению выведенной формулы. 2 × 6 × 9 × cos(65 ÷ 2) / 9 + 6 = 6 см.

Через две стороны и отрезки

Если вам известно 2 стороны треугольника и дано несколько отрезков на стороне, то вам нужно
руководствоваться следующей формулой:

L = √(b * c — a1 * a2)

где b, c — стороны, a1, a2 — длины отрезков, образованных на стороне.

Цифр после
запятой:

Результат в:

Пример. Есть треугольник АВС, у которого известны 2 стороны, 2 и 4 см
соответственно. Также дана пара отрезков на стороне, с показателем 2 см и 2 см. От нас просят найти
биссектрису треугольника АВС. Вместо b и c подставляем наши значения длин сторон, вместо а1 и а2 –
длины отрезков. Проводим вычисление и находим квадратный корень конечного результата. √(2 × 4 — 2 × 2) = 2 см.

Через все стороны

Чтобы отыскать длину биссектрисы треугольника, при известном значении каждой стороны фигуры, нужно
воспользоваться формулой ниже:

L = (√(bc (b + c + a)(b + c — a))) / (b + c)

где a, b, c — стороны.

Цифр после
запятой:

Результат в:

Пример. Нам дан некий треугольник АВС, известна каждая его сторона, допустим а = 10
см, b = 6 см, с = 8 см. Нам нужно отыскать биссектрису треугольника. Для этого подставляем все наши
известные значения в формулу. L = (√(6 * 8 * (6 + 8 + 10)(6 + 8 — 10))) / (6 + 8) = 4,8 см.

В прямоугольном треугольнике через гипотенузу и угол

Формула ниже слегка отличается от остальных, ведь тут использует понятие синуса и косинуса.

L = 2c / √2 * ((sin α * cos α) / (sin α + cos α))

где c — гипотенуза, sin α, cos α — угол.

Цифр после
запятой:

Результат в:

Именно данное вычисление поможет вам с поисками длины биссектрисы в прямоугольном треугольнике, если
вам известна одна гипотенуза и угол. «с» — гипотенуза, «а» — угол.

Пример. В прямоугольном треугольнике АВС известно значение гипотенузы и угла «а».
Пользуясь выведенной формулой, вы можете заметить, что от вас требуют синусы и косинусы угла «а».
Для того чтобы правильно посчитать, нужно воспользоваться специальной таблицей синусов и косинусов.
Далее решение не составит особого труда. Пусть гипотенуза c = 10 мм, угол α = 30 градусов,
тогда биссектриса L = 2* 10 / √2 * ((sin 30 * cos 30) / (sin 30 + cos 30)) = 4.48 мм.

В прямоугольном треугольнике через катеты

В прямоугольном треугольнике есть 2 катета и гипотенуза, как найти длину биссектрисы, если нам дано
только значение катетов треугольника. Для этого существует формула:

L = √2 * (ab / (a + b))

где «L» — искомая биссектриса, «а» и «b» — известное значение катетов прямоугольного
треугольника.

Цифр после
запятой:

Результат в:

Пример. Дан некий прямоугольный треугольник АВС, нам известна длина двух катетов,
5.5 см и 6 см. От нас просят найти длину биссектрисы треугольника АВС. √(2) × ((5.5 × 6) ÷ (5.5 + 6)) = 4,06 см.

Из острого угла в прямоугольном треугольнике через катет и угол

Если вам дан только катет и острый угол в прямоугольном треугольнике, используйте формулу:

L = b / cos β/2

где «b» — известный катет, а β — острый угол.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольный треугольник АВС. Известно, что катет «b» равен 9.7 см.,
угол β равен 45º. Нужно найти биссектрису. Нужно 9.7 поделить на косинус половины 45 град.
Подставляем значения в формулу: L = (9,7)/(cos(45)/(2)) = 10,5 см.

В равнобедренном треугольнике через боковую сторону и угол при основании

Для нахождения длины биссектрисы равнобедренного треугольника с помощью боковой стороны и угла при
основании можно воспользоваться данной формулой:

L = b * sin α

где b — боковая сторона, sin α — угол при основании.

Цифр после
запятой:

Результат в:

Пример. В условии дан равнобедренный треугольник. Известно, что боковая сторона
равна 12 см, а угол основания составляет 60 град. У нас есть все ключевые данные для решения, просто
подставляем их в формулу L = 12 * sin 60 = 10,4 см.

Из острого угла в прямоугольном треугольнике через катет и гипотенузу

Длину биссектрисы в прямоугольном треугольнике можно найти по формуле:

L = b * √(2c / b + c)

где «b» — гипотенуза, а «с» — катет.

Цифр после
запятой:

Результат в:

Пример. АВС –прямоугольный треугольник. Гипотенуза равна 8 см, а катет 3.5 см. L = 8 × √((2 × 3.5) ÷ (8 + 3.5)) = 4 см. Подставив значения в формулу,
мы получим результат, что биссектриса приблизительно равна 4 см.

В равнобедренном треугольнике через основание и угол при основании

Как и в предыдущих случаях, для данной задачи есть специальная формула:

L = a / 2 * tg α

где a — основание, tg α — угол при нижнем основании.

Цифр после
запятой:

Результат в:

Пример. Нам дан равнобедренный треугольник. В условии сказано, что основание «а»
равно 12 см, угол альфа – 60 град. Для решения поставим в формулу значения L = 12 ÷ 2 × tan(60) = 10.4 см

В равнобедренном треугольнике через основание и боковую сторону

Формула, по которой можно найти длину биссектрисы в равнобедренном треугольнике, если по условиям
дано основание и боковая сторона:

L = √(b² — a²/4)

где b и а — основание.

Цифр после
запятой:

Результат в:

Пример. В равнобедренном треугольнике АВС известно, что основание равно 9 см, а
боковая сторона 11 см. Нахождение биссектрисы происходит по формуле выше. L = √(9² — (11² ÷ 4)).
Следовательно, проведя сокращения, вычисления и округления у вас должен получится результат – 10 см.
Это и есть длина биссектрисы.

В равнобедренном треугольнике через боковую сторону и угол между боковыми сторонами

Как и все разы до этого, в данном случае применяется выведенная формула:

L = b * cos β/2

где b является боковой стороной, β – угол, который лежит между боковых сторон.

Цифр после
запятой:

Результат в:

Пример. Дан равнобедренный треугольник, боковая сторона которого равна 6.5 см.
Известно, что угол между боковыми сторонами равен 45 град. Нужно вычислить биссектрису. Используем
прямую формулу: L = 6.5 × cos(45 ÷ 2) = 6.005. После вычислений у нас
получается 6.005. Округляем до десятых и записываем в ответ 6 см.

В равностороннем треугольнике через сторону

Для нахождения длины биссектрисы в равностороннем треугольнике через сторону используйте формулу
ниже:

L = a√3 / 2

где а является стороной треугольника.

Цифр после
запятой:

Результат в:

Пример. Рассмотрим равносторонний треугольник, сторона которого равна 5.8 см. Задача
заключается в нахождение биссектрисы. Для решения у нас есть все нужные данные. Подставим их в
формулу: L = (5.8 × √(3)) ÷ 2. Проведя вычисление, мы получаем ответ 5.02,
это и есть значение длины биссектрисы.

Решение задач по геометрии в школе предусматривает детально рассмотрение понятия биссектрисы и всех
ее свойств включительно. Выходя из некоторых особенностей данного отрезка можно решать задачи
высокого уровня. Главное знать все тонкости и нюансы такого элемента как биссектриса.

В данной публикации приведены примеры наиболее распространенных формул, используемых при вычислении
длины биссектрисы в треугольнике. Каждая формула по-своему уникальна, но не является сложной.
Выучить их все будет трудно, но иметь всегда с собой вполне реально.

Источник