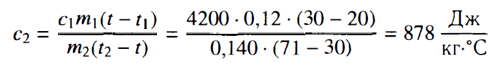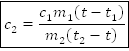Удельная теплоемкость цилиндра как найти

Привет
Измерение удельной теплоемкости  твердого тела
Цель работы: определить удельную теплоемкость металлического цилиндра.
Приборы и материалы: стакан с водой, калориметр, термометр, весы, гири, металлический цилиндр на нити, сосуд с горячей водой.
Ход работы:
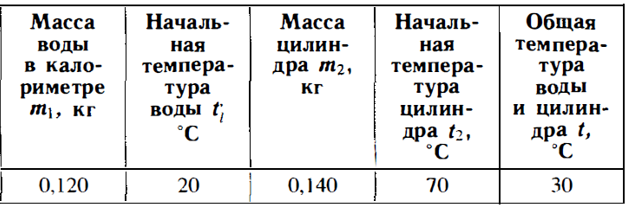
1. Нальем в калориметр воду массой 0,120 кг и измерим ее температуру (20°С).
2. Нагреем цилиндр в сосуде с горячей водой. Измерим температуру воды (70°С), и опустим цилиндр в колориметр с холодной водой.
3. Немного подождем и измерим температуру воды в калориметре (ЗО0С).
4. Вытащим цилиндр из калориметра, обсушим его и измерим его массу на весах (0,140 кг).
5. Все результаты измерений занесем в таблицу и рассчитаем удельную теплоемкость металлического цилиндра.
Результаты:

Вычислим удельную теплоемкость металлического цилиндра по формуле с2 =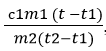где с2  – удельная теплоемкость металлического цилиндра; с1 = 4200   – удельная теплоемкость воды; m1 – масса воды в калорифере; t – температура нагретой цилиндром воды в калорифере; t1 – температура холодной воды; t2 – масса металлического цилиндра; t2 – температура нагретого металлического цилиндра.

Выводы: Удельная теплоемкость металлического цилиндра равна 878 , что близко к значению удельной теплоемкости для алюминия. Полученное значение несколько меньше табличного, что связано с невысокой точностью приборов и наличием теплообмена.

Цель этой работы: с помощью экспериментальной
установки определить удельную теплоёмкость металлического цилиндра и
установить, из какого материала он изготовлен.

Для выполнения этой работы мы будем использовать оборудование
из комплекта № 7 в составе: измерительный цилиндр (мензурка), термометр,
калориметр, весы электронные и металлический цилиндр № 1 с нитью. На столе у
проверяющих дополнительно вы найдёте: чайник с термостатом, термометр,
измеряющий температуру воздуха в помещении, и графин с водой комнатной
температуры.

Прежде чем приступить к работе давайте с вами вспомним, изменить
состояние термодинамической системы можно двумя способами.  Первый
характеризуется передачей энергии в процессе механического взаимодействия тел.
Такую форму передачи энергии в термодинамике (как и в механике) называют работой.

Второй способ передачи энергии осуществляется при
непосредственном обмене энергией между хаотически движущимися частицами
взаимодействующих тел. Если, например, привести в соприкосновение два тела с
разными температурами, то частицы более нагретого тела будут передавать часть
своей энергии частицам более холодного тела. В результате внутренняя энергия
первого тела уменьшается, а второго — увеличивается.

Давайте
вспомним, что скалярная физическая величина, равная изменению внутренней
энергии тела в процессе теплопередачи без совершения механической работы,
называется количеством теплоты.

Количество
теплоты, полученное телом при его нагревании (или отданное им при охлаждении)
зависит от трёх факторов: рода вещества, из которого изготовлено тело, массы
тела и разности температур тела в конечном и начальном состояниях.

В записанной
формуле с — это удельная теплоёмкость вещества. Она равна
количеству теплоты, которое нужно сообщить телу массой 1 кг для его
нагревания на 1 ^оС:

Из
определения следует, что единицей удельной теплоёмкости является Джоуль,
делённый на килограмм, градус Цельсия:

Именно
удельную теплоёмкость вещества нам и предстоит с вами искать в сегодняшней
работе. Но анализ оборудования нам подсказывает, что для успешного выполнения
данной работы нам необходимо вспомнить ещё и уравнение теплового баланса:
при теплообмене между телами, образующими теплоизолированную систему, суммарное
количество теплоты, полученное ими, равняется нулю:

В записанной
формуле количество теплоты считается положительным, если тело получает энергию
(нагревается), и отрицательным — если тело энергию отдаёт (то есть остывает.

Теперь можно
приступить к самой работе. Итак, для начала нарисуем рисунок нашей
экспериментальной установки (если этого будет требовать условие). Для начала мы
нарисуем стакан с водой — наш калориметр. Внутрь калориметра вставим термометр,
на котором укажем начальную температуру воды. Рядом нарисуем ещё один
калориметр с водой и термометром. Однако теперь внутри калориметра дорисуем
цилиндр. На термометре укажем конечную температуру воды.

Далее нам с
вами необходимо записать формулы, которыми будем пользоваться при выполнении
работы. Во-первых, мы с вами запишем формулы для определения количества
теплоты, которое выделяется при остывании цилиндра, и количества теплоты,
которое получает вода:

В записанных
формулах:

с_м — удельная теплоёмкость металла, из которого
изготовлен цилиндр (искомая величина);

m_м — масса цилиндра, которую можно
определить с помощью весов;

t₁ — температура горячей воды и, соответственно,
начальная температура цилиндра;

с_в — это удельная теплоёмкость воды (табличная величина):

m_в — масса воды;

t₂ — начальная температура холодной воды, измеренная с
помощью термометра;

t — конечная температура воды и
цилиндра, измеренная с помощью термометра.

Как было
указано ранее, в процессе теплообмена сумма количества теплоты, полученное
водой и количества теплоты, которое отдал металлический цилиндр, должна
равняться нулю:

Решаем
полученное уравнение относительно искомой величины — удельной теплоёмкости
цилиндра:

Так же мы с вами
должны записать формулу, по которой можно определить массу воды, зная её
плотность (это табличное значение) и объём:

Тогда наша
расчётная формула примет тот окончательный вид:

Результаты
прямых измерений мы с вами, для удобства, будем заносить в таблицу: объём воды,
начальная температура воды, масса цилиндра, начальная температура цилиндра и
общая температура воды и цилиндра.

Теперь
приступим непосредственно к работе. Итак, для начала налейте из графина в
калориметр примерно 150 мл воды комнатной температуры. Измерьте и запишите в
таблицу объём и температуру этой воды.

Подойдите с
калориметром к столу экспертов и, получив из чайника с термостатом цилиндр на
нитке, сразу же погрузите его в калориметр. Не забудьте посмотреть или спросить
температуру воды в чайнике — это будет начальная температура цилиндра.

На рабочем
месте опустите в калориметр с погруженным телом термометр и, перемешивая воду,
наблюдайте за повышением её температуры. Когда температура воды в калориметре
перестанет расти, запишите в таблицу значение окончательно установившейся
температуры.

Достаньте
цилиндр из калориметра и, промокнув его фильтровальной бумагой, определите на
весах его массу и запишите в таблицу.

Прямые
измерения мы с вами завершили. Теперь значения всех найденных величин
подставляем в нашу расчётную формулу.

По таблице
(или в начале листочка с заданиями) определяем, что цилиндр изготовлен из
стали.

Тогда в выводе
мы можем написать, что удельная теплоёмкость металлического цилиндра равна
500 Дж/(кг ∙ ℃). Цилиндр изготовлен
из стали.

Посмотреть
видео по этапам выполнить работу.

https://youtu.be/eO_9Uxju7ec

Работу
пишем на двойном листочке в клеточку.

Подписываем
в правом верхнем углу Фамилия Имя

Одиннадцатое
ноября

Лабораторная
работа № 2

«Измерение
удельной теплоемкости твердого тела»

Цель: научится определять удельную теплоемкость
твердого тела путем сравнения его с теплоемкостью воды.

Оборудование: калориметр,
металлический цилиндр на нити, рычажные весы, набор гирь, термометр, стакан с
холодной водой, сосуд с горячей водой.

Ход
работы

1.    
Определяем массу металлического цилиндра с помощью весов.

2.    
Поместим металлический цилиндр в стакан с горячей водой и
измерим термометром ее температуру. Она будет равняться температуре цилиндра,
т. к. через определенное время температуры воды и цилиндра сравняются.

3.    
Затем нальем в калориметр холодную воду и измерим ее
температуру.

4.    
После этого поместим привязанный на нитке цилиндр в калориметр с
холодной водой и, помешивая в нем воду термометром, измерим установившуюся в
результате теплообмена температуру.

5.    
Полученные результаты занесем в таблицу.

№	Масса воды в калориметре , кг	Начальная температура воды , С	Масса цилиндра , кг	Начальная температура цилиндра , С	Общая температура воды и цилиндра t, С
1.	0,150	23	0,168	79	28
2.

5. Произведем
расчеты:

Соответственно получаем следующие уравнения. Для нагрева воды
необходимо количество теплоты:

 

При остывании металлического цилиндра выделится количество
теплоты:Так как в процессе теплообмена количество
теплоты, полученное водой, равно количеству теплоты, которое отдал
металлический цилиндр:

Следовательно, удельная теплоемкость материала цилиндра:

Полученную
удельную теплоёмкость сравниваем с табличными данными:

Из таблицы видим,
что цилиндр может быть изготовлен из таких материалов: меди, цинка или латуни.

6. Выполняем по
эталону опыт № 2.

Вывод: Я научился(-ась) определять удельную теплоемкость твердого
тела путем сравнения его с теплоемкостью воды.

1. Цель лабораторной работы, объект исследования, приборы и материалы

Тема се­го­дняш­не­го за­ня­тия по­свя­ще­на тому, каким об­ра­зом можно опре­де­лить удель­ную теп­ло­ем­кость ве­ще­ства опыт­ным путем, т. е. на прак­ти­ке. Кон­крет­но, мы рас­смот­рим опре­де­ле­ние теп­ло­ем­ко­сти на при­ме­ре твер­до­го тела – ме­тал­ли­че­ско­го (ла­тун­но­го) ци­лин­дра.

Цель ра­бо­ты:опре­де­лить удель­ную теп­ло­ем­кость ме­тал­ли­че­ско­го ци­лин­дра.

Объ­ект ис­сле­до­ва­ния:ла­тун­ный ци­линдр, под­ве­шен­ный на нити.

При­бо­ры и ма­те­ри­а­лы: ме­тал­ли­че­ский ци­линдр на нити (рис. 1), ста­кан с го­ря­чей и ста­кан с хо­лод­ной водой (рис. 2), два тер­мо­мет­ра (рис. 3), весы (рис. 4), ка­ло­ри­метр (рис. 5).

Рис. 2. Ста­кан с водой

Рис. 3. Тер­мо­метр

Рис. 4. Весы

Рис. 5. Ка­ло­ри­метр

2. Ход работы

Ход ра­бо­ты:

1. По­ме­стим ме­тал­ли­че­ский ци­линдр в ста­кан с го­ря­чей водой и из­ме­рим тер­мо­мет­ром ее тем­пе­ра­ту­ру, она будет рав­нять­ся тем­пе­ра­ту­ре ци­лин­дра, т. к. через опре­де­лен­ное время тем­пе­ра­ту­ра воды и ци­лин­дра срав­ня­ют­ся.

2. Затем на­ли­ва­ем в ка­ло­ри­метр хо­лод­ную воду и из­ме­ря­ем ее тем­пе­ра­ту­ру.

3. После этого по­ме­ща­ем при­вя­зан­ный на нитке ци­линдр в ка­ло­ри­метр с хо­лод­ной водой и, по­ме­ши­вая в нем воду тер­мо­мет­ром, из­ме­ря­ем уста­но­вив­шу­ю­ся в ре­зуль­та­те теп­ло­об­ме­на тем­пе­ра­ту­ру.

3. Обработка данных и вычисление результата

Об­ра­бот­ка дан­ных и вы­чис­ле­ние ре­зуль­та­та:

Из­ме­рен­ная уста­но­вив­ша­я­ся ко­неч­ная тем­пе­ра­ту­ра в ка­ло­ри­мет­ре и осталь­ные дан­ные поз­во­лят нам рас­счи­тать удель­ную теп­ло­ем­кость ме­тал­ла, из ко­то­ро­го из­го­тов­лен ци­линдр. Вы­чис­лять ис­ко­мую ве­ли­чи­ну мы будем ис­хо­дя из того, что, осты­вая, ци­линдр от­да­ет ровно такое же ко­ли­че­ство теп­ло­ты, что и по­лу­ча­ет вода при на­гре­ва­нии, про­ис­хо­дит так на­зы­ва­е­мый теп­ло­об­мен.

Со­от­вет­ствен­но по­лу­ча­ем сле­ду­ю­щие урав­не­ния. Для на­гре­ва воды ко­ли­че­ство теп­ло­ты:

, где:

 удель­ная теп­ло­ем­кость воды (таб­лич­ная ве­ли­чи­на), ;

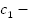
 масса воды, ко­то­рую можно опре­де­лить с по­мо­щью весов, кг;

 ко­неч­ная тем­пе­ра­ту­ра воды и ци­лин­дра, из­ме­рен­ная с по­мо­щью тер­мо­мет­ра, ^o;

 на­чаль­ная тем­пе­ра­ту­ра хо­лод­ной воды, из­ме­рен­ная с по­мо­щью тер­мо­мет­ра, ^o.

Для осты­ва­ния ме­тал­ли­че­ско­го ци­лин­дра ко­ли­че­ство теп­ло­ты:

, где:

 удель­ная теп­ло­ем­кость ме­тал­ла, из ко­то­ро­го из­го­тов­лен ци­линдр (ис­ко­мая ве­ли­чи­на), ;

 масса ци­лин­дра, ко­то­рую можно опре­де­лить с по­мо­щью весов, кг;

 тем­пе­ра­ту­ра го­ря­чей воды и, со­от­вет­ствен­но, на­чаль­ная тем­пе­ра­ту­ра ци­лин­дра, из­ме­рен­ная с по­мо­щью тер­мо­мет­ра, ^o;

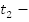
 ко­неч­ная тем­пе­ра­ту­ра воды и ци­лин­дра, из­ме­рен­ная с по­мо­щью тер­мо­мет­ра, ^o.

За­ме­ча­ние. В обеих фор­му­лах мы вы­чи­та­ем из боль­шей тем­пе­ра­ту­ры мень­шую для опре­де­ле­ния по­ло­жи­тель­но­го зна­че­ния ко­ли­че­ства теп­ло­ты.

Как было ука­за­но ранее, из-за про­цес­са теп­ло­об­ме­на между хо­лод­ной водой и ме­тал­ли­че­ским ци­лин­дром их ко­ли­че­ства теп­ло­ты равны:

.

Сле­до­ва­тель­но, удель­ная теп­ло­ем­кость ма­те­ри­а­ла ци­лин­дра:

По­лу­чен­ные ре­зуль­та­ты в любой ла­бо­ра­тор­ной ра­бо­те удоб­но за­пи­сы­вать в таб­ли­цу, при­чем, про­во­дить для по­лу­че­ния усред­нен­но­го мак­си­маль­но точно при­бли­жен­но­го ре­зуль­та­та несколь­ко из­ме­ре­ний и вы­чис­ле­ний. В нашем слу­чае таб­ли­ца может вы­гля­деть при­мер­но сле­ду­ю­щим об­ра­зом:

Вывод:вы­чис­лен­ное зна­че­ние удель­ной теп­ло­ем­ко­сти ма­те­ри­а­ла ци­лин­дра .

Се­год­ня мы рас­смот­ре­ли ме­то­ди­ку про­ве­де­ния ла­бо­ра­тор­ной ра­бо­ты по из­ме­ре­нию удель­ной теп­ло­ем­ко­сти твер­до­го тела. На сле­ду­ю­щем уроке мы по­го­во­рим о вы­де­ле­нии энер­гии при сго­ра­нии топ­ли­ва.

Задание: измерить теплоемкость стаканов и удельные теплоемкости латунного и дюралевого цилиндров

Оборудование и принадлежности: установка для проведения измерений.

ОПИСАНИЕ УСТАНОВКИ

Внешний вид установки показан на рисунке 1. На передней панели размещен экран 1, клавиатура управления 2 и датчик напряжения и силы тока 3. На задней панели расположен выключатель. Под теплоизолирующей крышкой 4 расположены два стакана с цилиндрами (рис. 2): первый 5 с латунным цилиндром, второй 6 с дюралевым цилиндром. В основании каждого стакана установлен цифровой термометр для измерения температуры стакана (нагревателя) (THt1 и THt2). В верхнем основании цилиндров установлены такие же термометры для измерения температуры цилиндров (TVl1 и TVl2). Установка готова к работе (на экране высвечивается надпись «ENABLE»), если температура первого стакана превышает температуру воздуха (TAir) внутри прибора не более чем на 2 °С, в противном случае необходимо подождать, пока вентиляторы не охладят стакан 1. Поэтому, если предполагается работа с двумя стаканами, надо начинать со стакана 2. Управление прибором осуществляется с клавиатуры (рис. 3).

Последовательным нажатием клавиши «ВЫБОР» осуществляется выбор стакана 1 или стакана 2. Последовательным нажатием левой и правой клавиш во втором ряду сверху можно изменять максимальную температуру нагревателя (от 50 °С до 90 °С). Точно так же левая и правая клавиши в третьем ряду сверху позволяют выбрать мощность нагревателя (от 60% до 100%). При нажатии клавиши «ВВОД» начнется нагрев выбранного стакана с последующим его охлаждением. Средняя клавиша первого ряда сверху – просмотр нагрева, а средняя клавиша второго ряда сверху – просмотр охлаждения выбранного стакана.

При подключенном принтере клавиша «ПЕЧАТЬ» позволяет распечатать графики, выведенные на экран. Клавиша «СБРОС» активирована до нажатия клавиши «ВВОД». То есть, процесс нагрева или охлаждения можно остановить только выключением прибора.

При нагревании на датчике 3 установки через каждые 4 с выводятся значения напряжения и силы тока нагревателя, что позволяет определить мощность и количество теплоты, выделившейся на нагревателе. Установка запоминает значения температуры стакана и цилиндра через каждые 4 с, строит графики зависимости температур стакана и цилиндра от времени. Эту информация отображается на экране.

В процессе остывания установка запоминает значения температуры стакана и цилиндра через каждые 2 с и строит графики зависимости температур стакана и цилиндра от времени. Эта информация также отображается на экране.

Нагреватель вмонтирован в дно стакана. Термометр стакана расположен рядом с нагревателем, его показания равны температуре нагревателя. Когда цилиндр вставлен в стакан, то температура нижнего основания цилиндра также равна температуре нагревателя, которую определяет термометр стакана.

Мощность нагревателя вычисляется по формуле

P = I(U – 0,33I), (1)

Где I и U – сила тока и напряжение, показываемые датчиком 3.

ЭЛЕМЕНТЫ ТЕОРИИ

Общие сведения. Теплоемкостью тела называется физическая величина, равная отношению бесконечно малого количества теплоты, полученного телом, к соответствующему приращению его температуры

. (2)

Из этого определения следует, что теплоемкость тела равна количеству теплоты, которое необходимо сообщить телу для изменения его температуры на 1 K.

Теплоемкость зависит от массы тела и условий, в которых телу сообщается теплота и изменяется его температура. Например, теплоемкость газов при постоянном объеме значительно отличается от их теплоемкости при постоянном давлении.

Теплоемкость единицы массы тела называется Удельной теплоемкостью тела

. (3)

Количество теплоты, отдаваемое в единицу времени нагретым телом (мощность тепловых потерь), прямо пропорционально разности температур между телом и окружающей средой:

Ps = A0(T –T0), (4)

Где A0 – коэффициент теплового рассеяния. Пусть тело теплоемкости C, находящееся в воздухе температуры T0, получает теплоту от нагревателя мощности P. Запишем уравнение теплового баланса для бесконечно малого промежутка времени DT:

PdT = Cdt + A0(T – T0)DT, (5)

Решение этого уравнения имеет вид:

. (6)

Если система теплоизолирована, т. е. коэффициент теплового рассеяния A0 = 0, то из (5) следует, что

. (7)

Пусть в теплоизолированной системе происходит теплообмен между двумя телами, начальные температуры которых равны T01 и T02 (T01 > T02).

соответственно теплоемкости и C1, C2 и. Уравнение теплового баланса для бесконечно малого промежутка времени DT можно записать в виде:

A(t1 – t2)dT = — Cdt1, (8)

A(t1 – t2)dT = cmdt2, (9)

Где A – неизвестный коэффициент теплоотдачи первого тела, C – его теплоемкость, C и M – удельная теплоемкость и масса второго тела, T1 и T2– температуры тел в данный момент времени. Из (8) и (9) получаем уравнение

(C +Cm)A(T1 – T2)DT = —CmCd(T1 – T2), (10)

Решение которого имеет вид

, (11)

Где

(12)

Время релаксации, то есть время, в течение которого разность температур уменьшается в Е раз. Время релаксации находим из соотношения (11)

. (13)

Температуры тел

, (14)

, (15)

Где Tr – конечная, или равновесная температура тел.

Теория метода. Для измерения теплоемкости С стакана и удельной теплоемкости С цилиндра массой M сначала нагреваем стакан, цилиндр вынут из стакана и не нагревается. Затем цилиндр вставляем в стакан и закрываем теплоизолирующей крышкой. Между цилиндром и стаканом происходит теплообмен, пока их температуры не будут одинаковы.

При нагревании стакана количество теплоты, которое выделяет нагреватель, идет на нагревание стакана и частично рассеивается в воздухе. Особенности конструкции установки приводят к тому, что температура воздуха, окружающего стакан, будет повышаться. Поэтому изменение температуры стакана не будет в точности описываться уравнением (6).

Зависимость температуры стакана от времени будем аппроксимировать квадратичной параболической функцией

T = A0 + A1T + A2T2. (16)

Ограничившись первыми тремя членами разложения экспоненты (6) в ряд, получим

. (17)

Сравнивая (17) с (16), получим выражения для определения теплоемкости стакана и коэффициента тепловых потерь:

(18)

(19)

Определив значения температуры стакана T для трех моментов времени нагревания стакана T (в начале, середине и конце выбранного участка графика зависимости температуры от времени), получим три уравнения для определения коэффициентов A0, A1, A2.

Для более точного определения коэффициентов A0, A1, A2 необходимо применить Метод наименьших квадратов. Пусть в эксперименте получен ряд значений температуры Ti для соответствующих моментов времени TI, I = 1, 2, …N. Коэффициенты A0, A1, A2 нужно определить так, чтобы выражение

(20)

Было минимальным. Для этого необходимо выполнение условий

, (21)

, (22)

. (23)

Введем обозначения:

, , , , , ,

, , . (24)

Тогда

Ti = A0 + A1TI + A2 Zi, (25)

И из соотношений (21 – 23) получаем уравнения

A0 + <T>a1 + <z>a2 = <t>, (26)

N<T>a0 + S2a1 + T1a2 = S1, (27)

S2a0 + T1a1 + T2a2 = V1. (28)

Для определения A0, A1, A2.

Для определения удельной теплоемкости цилиндра используем процесс релаксации (остывания) стакана с цилиндром. Стакан с цилиндром находятся в термостате. Пренебрегая тепловыми потерями, запишем уравнение теплового баланса для небольшого промежутка времени (оно следует также из формул (8) и (9)):

CmDT2 = —CDT1, (29)

Где DT1 и DT2 – изменения температуры стакана и цилиндра за один и тот же промежуток времени. Отсюда находим удельную теплоемкость цилиндра

. (30)

По формуле (13) можно определить время релаксации стакана с цилиндром, а из (12) – коэффициент A:

(31)

УПРАЖНЕНИЯ

1. Включить установку.

2. Когда на экране появится надпись «ENABLE», нажать клавишу «ВЫБОР» и выбрать стакан 2.

3. Выбрать конечную температуру стакана и мощность нагревателя, после чего нажать клавишу «ВВОД».

4. Записать значения напряжения и силы тока.

5. После окончания процесса нагревания, следуя указаниям установки, вставить цилиндр в стакан и закрыть крышку.

6. После окончания измерений со стаканом 2 выполнить пункты 2 – 5 со стаканом 1.

7. После окончания измерений снять результаты измерений с помощью средних клавиш первого и второго ряда клавиатуры (рис. 3) (или распечатать результаты, если подключен принтер).

8. Определить коэффициенты A0, A1, A2 уравнения (16) (по формулам (26) – (28) метода наименьших квадратов или методом трех точек графика T(T)). Из уравнений (18) и (19) вычислить теплоемкость и коэффициент тепловых потерь стаканов, из (30) – удельную теплоемкость цилиндров, из (13) и (31) – время релаксации и коэффициент теплоотдачи.