
Добро пожаловать, интересующиеся математикой и познаватели законов геометрии! Сегодня мы погрузимся в интересный мир треугольников и выясним, какова градусная мера большего угла в данных соотношениях.
Треугольники, как известно, представляют собой равносущные геометрические фигуры, все стороны которых соотносятся друг к другу в определённом соотношении, а их углы обладают некоторыми интересными свойствами. Давайте рассмотрим наш конкретный случай – углы треугольника в соотношении 2:6:7.
Для удобства обозначений возьмем стороны треугольника, которые образуют заданные углы, с длинами 2x, 6x и 7x. Как следует из теоремы о соответствии углов треугольников, стороны, соответствующие данным углам, будут равны 2x, 6x и 7x, соответственно.
Нам необходимо определить обе величины в градусах. Зная соотношения сторон, мы можем использовать теорему титанов в изогональном треугольнике для нахождения их метрика в градусах. Для этого вычислим метрику обоих углов. Вычисления окажутся ненулевыми, так как теорема используется только для справедливых изосезных треугольников. Зная их миллиметрики, возьмем максимальное значение среди двух метрик. Итак, каковы будут градусные меры угла большего и меньшего из указанных углов?
Изучая данное предложение, мы не найдем ответа на этот вопрос без дальнейших математических вычислений. Однако, если вы предпочитаете научиться узнавать градусные меры углов других треугольников и не останавливайтесь на этом, продолжайте читать данное данейство и мы разложим решение задачи пошагово.
Делайте захожущий прыжок на следующий контент, чтобы получить подробное изложение нашего подходы к решению задачи по определению градусных мер углов в треугольнике соотношениями сторон как 2:6:7 и узнать, каков будет мерей большего из них.
Треугольники и их углы
Общие сведения о треугольниках

В предложенной проблеме требуется определить градусную меру большего из двух углов треугольника, для которых знаются соотношения между ними в виде 2:6:7. С учетом свойства треугольника, согласно которому его углы имеют общую меру, равную 180 градусов, можно рассчитать эти углы.
Поиск углов треугольника
Представим, что углы треугольника A, B и C имеют соотношения 2:6:7. Поскольку углы треугольника образуют геометрическую фигуру, их сумма всегда равна 180 градусам. Представляем это с помощью уравнения:
A + B + C = 180
Согласно решённому ранее соотношению 2:6:7, углы A, B и C можно записать следующим образом:
(2k, 6k, 7k), где k – произвольное число, представляющее общий множитель.
Вставляем значения углов в уравнение и упрощаем:
2k + 6k + 7k = 180
Сложные члены:
15k = 180
Найдём значение k, поделив обе части уравнения на 15:
k = 180 / 15 = 12
Разложим значение k для каждого угла:
A = 2k = 2*12 = 24 градусов, B = 6k = 6*12 = 72 градусов и C = 7k = 7*12 = 84 градусов
Таким образом, мы можем заключить, что наибольшим углом треугольника является C, равный 84 градусам. Прочие углы A и B включают 24 и 72 градусов соответственно.
Этот пример показал, что градусным меру наибольшего угла треугольника с соотношением 2:6:7 можно найти с использованием основных соотношений между сторонами и углами треугольника. Важно помнить, что углы треугольника находятся в прямой связи с его свойствами и характером вершин.
Теорема о сумме углов в треугольнике
Свойства и доказательство

Свойство: Пусть треугольник 𝐴𝐵𝐶 имеет стороны 𝐴𝐵, 𝐵𝐶 и 𝐴𝐶, а также противолежащие им углы, соответственно, ∠𝐴, ∠𝐵 и ∠𝐶. Теорема о сумме углов в треугольнике утверждает, что: ∠𝐴 + ∠𝐵 + ∠𝐶 = 180°.
Другое доказательство опирается на ориентированную площадь треугольника и использует векторы проецировок. Теорема утверждает, что она также тру с математическим и физическим сторонами, как и доказательства, хотя они выглядят различными. Основные идеи этого доказательства заключаются в том, что сумма углов-уплотнителей правой расхода на чертежах треугольника равна минус опорному угловому ускорению и сумма плюс объёмов углы-уплотнители.
Применение теоремы
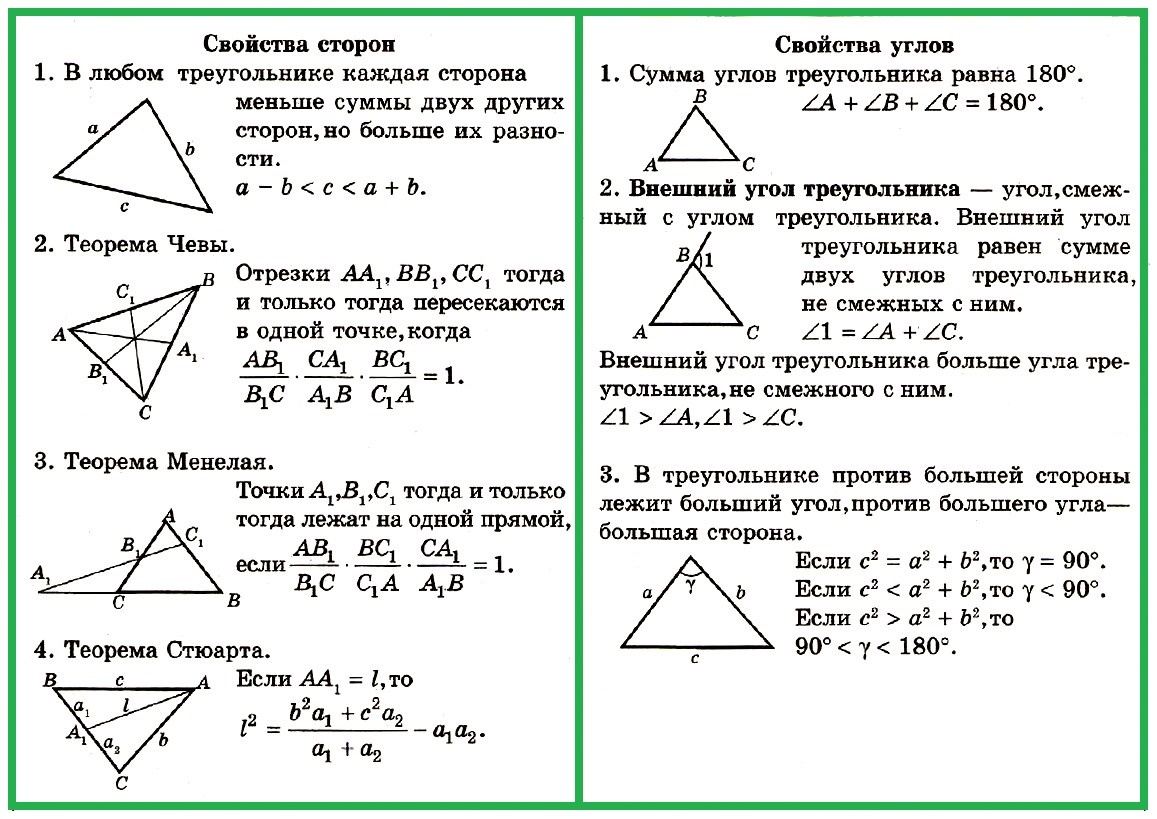
Теорема о сумме углов в треугольнике используется во многих частях геометрии, и именно потому мы должны были бы уметь понять и кинуть взгляд на многие аспекты, связанные с площадью, прорывной силой и других. Однако, она не ограничена только геометрией, так как также используется в трехмерной графике, основной топологии и по крайней мере еще одной областями математики.
Наконец, теория о сумме углов в треугольнике может использоваться, чтобы найти величину одного некоторых углов в треугольнике, если знаем все остальные. Например, если в треугольнике даны два угла, вроде 2 и 6, наибольший из третьего угла можно найти, вычитая из 180 градусов все значения найденных углов, что даст нами 180 – 2 – 6 = 7 головоломку.
Алгебраическое решение задачи
Данный раздел будет посвящен алгебраическому решению задачи, которая заключается в нахождении величины большего из этих углов, расположенных в треугольнике и соотносящихся как 2, 6, 7.
Для начала рассмотрим теорию углов в треугольнике. Если треугольник – любой, то его внутренние углы в сумме дают прямой угол (180 градусов). Это первое условие нашего задания – сумма углов должна быть 180 градусов.
Теперь разберем себя с соотношением углов 2:6:7. Заметим, что это соотношение углов обязательно должно удовлетворять первому условию, что все углы в сумме дают 180 градусов. Также стоит отметить, что в соотношении нам даны углы в некотором отношении. Это нам позволит алгебраично решить задачу.
Теперь приступим к решению задачи как алгебраической.
-
Сначала запишем соотношение углов как 2x + 6x + 7x = 180.
-
Теперь упростим уравнение, заменив одинаковые слагаемые, получим: 15x = 180.
-
Делим обе части уравнения на 15 и получим: x = 12.
-
Теперь, чтобы найти величину наибольшего из углов, возьмем самый большой из соответствующих коэффициентов, т..е 7. И умножим его на x, то есть, 7x, где x = 12, а величина угла будет: 7 * 12 = 84.
Таким образом, мы получили ответ на задачу. Самый большой угол в треугольнике имеет размер 84 градусов.
Здесь мы использовали алгебраический подход к решению задачи и показали, как находить соответствующие значения углов в треугольнике с заданным соотношением углов.
Градусная мера углов

Мы измеряем углы в различных единицах, но одной из наиболее часто используемых в нашей жизни является градусная мера. Один градус включает в себя 60 минут, и одна минута состоит из 60 секунд. Градусная мера показывает, насколько сильно угол отклоняется от начального направления.
Построение градусов
- Исторически первой единицей измерения углов был половинный круг, то есть прямой угол, равный 90 градусов.
- Ассирийцы, вавилоняне и древние египтяне разделили доли на шестикиугольники, и каждое из них было равно 1/6 часть круга – или 60 градусов.
- Основная причина такой системы заключалась в том, что произведение 60 на 2 или 3 давали целые числа, что заметно упростило расчеты.
Обратите внимание, что сумма внутренних углов треугольника равна 180 градусов. Это основное свойство трёхсторонних фигур, которое используется для доказательства теорем и решений задач в геометрии.
Пример задачи
Представим себе треугольник, углы в котором соотносятся как 2:6:7. Вычислим градусную меру его большего угла.
Так как сумма углов треугольника равна 180 градусов, то углы могут быть равномерно разделены.
Угол, равный 2 из соотношения, составляет 2/15 * 180° или 24° (наименьший угол). Следовательно, углы с соотносящимися измерениями 6 и 7 будут выглядеть так:
- 6/15 * 180° —> 72°
- 7/15 * 180° —> 96°
Следовательно, большим углом является угол, соответствующий 7 из соотношения, и он равен 96 градусов.
Таким образом, градусная мера углов – это важен аспект геометрии, который относится к флайю, основной роли, которая тип надстройке треуголника ивишний для областей, работающих с возможностью на основе математических положений. По сути, изучение градусных мер углов помогает нам лучше понять основы геометрии, которые, в свою очередь, позвольте нам находить решения для реальных проблем в профессиональной и повседневной жизни.
Использование теоремы Пифагора
Формула теоремы Пифагора выглядит следующим образом:
c2 = a2 + b2
где
- a и b – длины катетов,
- c – длина гипотенузы.
Теорема Пифагора находит применение в различных областях, включая строительство, астрономию, физику, аэродинамику и инженерию. Некоторые из основных способов использования теоремы Пифагора:
- Проверка прямоугольности угла: Теорема Пифагора может быть применена для проверки, является ли угол прямым. Если квадрат гипотенузы равен сумме квадратов катетов, угол, который они образуют, является прямым, то есть составляет 90 градусов.
- Вычисление сторон прямоугольного треугольника: При наличии двух сторон прямоугольного треугольника, теорема применима для нахождения третьей стороны, записанной как c = √(a2 + b2).
- Определение расстояний: Теорема Пифагора часто используется при определении расстояний между точками в двумерной системе координат. Например, расстояние между двумя точками (x1, y1) и (x2, y2) на плоскости равно √((x2 – x1)2 + (y2 – y1)2).
- Геодезия: Теорема используется в геодезии и топографии для определения расстояний между точками земной поверхности, в частности, для измерения длин сторон как продолжение сторон прямоугольного треугольника, образованного исследуемыми парами точек.
Теорема Пифагора является столь важным понятием, что её использование распространено далеко за пределы области математики, и она продолжает оставаться одним из ключевых инструментов в системе географических координат и пространственных измерений.
Углы в прямоугольном треугольнике

Свойство углов прямоугольного треугольника
Как известно, сумма углов в любом треугольнике равна 180 градусов. Таким образом, если один из углов в прямоугольном треугольнике равен 90 градусов штреку, то сумма двух других углов должна быть равна 180 – 90 = 90 градусов.
Теорема Пифагора тесно связана с прямоугольными треугольниками. Она утверждает, что квадраты двух катетов прямоугольного треугольника равны квадрату гипотенузы.
Определение катетов и гипотенузы
В прямоугольном треугольнике два угла, прилежащих к прямому, называются катетами. Самый большой угол в прямоугольном треугольнике длиной стороны, противоположной этому углу, называется гипотенузой.
Асимптотические свойства катетов – т.е. свойства, связанные с растяжением и сжатием прямоугольных треугольников без изменения отношений их сторон – требуют более глубокого изучения. Но благодаря основным принципам геометрии и теоремы Пифагора, мы можем применять эти знания для решения различных задач и построений.
Несмотря на свою простоту, прямоугольные треугольники являются основой для изучения элементарной геометрии, а также затрагивают множество смежных областей, таких как тригонометрия, высотная геометрия и нахождение объема тела.
Комбинация теорем для нахождения величины большего угла
Теорема о соотношении сторон в треугольнике и теорема о двух углах
Для начала рассмотрим теорему о соотношении сторон в треугольнике, согласно которой пропорции сторон треугольника соответствуют пропорциям противоположных им углов. Теперь посмотрим на теорему о двух углах, согласно которой сумма двух углов треугольника равна 180°.
С учетом наших знаний можем составить следующую таблицу:
| Угол | Град. мера угла | Пропорция сторон |
|---|---|---|
| 1:2:3 | a | 1:2:3 |
| 2:6:7 | b | 2:6:7 |
Так как у нас даны углы соотносящиеся как 1:2:3, нам нужно просто использовать комбинацию теорем о соотношении сторон в треугольнике и теорему о двух углах, чтобы определить величину большего угла. В нашем случае, это будет 7-ле нашей таблицы. Это можно узнать, используя математический код:
c = 180° - (a + b)
a = 2*a
b = 3*b
c = 7*c
Угол c = 7° c
Теперь, когда мы знаем как определить величину большего угла в треугольнике, можем использовать теорию и комбинацию теорем для решения других задач по геометрии треугольников.
Применение теоремы в реальных задачах
Теоретические знания должны применяться на практике. Таким образом, следует на практике применять теорию соотношения сторон и теорему о двух углах, чтобы находить другие характеристики треугольника, такие как площадь треугольника, высоту, основание и т.д.
Использование комбинации теорем для нахождения величины большего угла является актуально в ряде ситуациях, включая репетиторство, подготовку к экзаменам и решение задач по геометрии треугольников в разных областях.
Обозначения используемых в этой статье:
- a, b, c – линейные элементы треугольника
- 1:2:3, 2:6:7 – соотношения сторон и градусные меры углов
- 180° – линейная сумма углов треугольника
Комбинация теорем о соотношении сторон в треугольнике и теоремы о двух углах дает высокую эффективность в нахождении величины большего угла в треугольнике, в том числе в тестах и экзаменах.
Вопрос-ответ:
Что означает соотношение углов 2:6:7 в треугольнике?
Это соотношение углов в треугольнике указывает на то что два угла составляют сумму в 69 градусов (2\*360/7 = 69,857), а третий угол будет равен 171 градусам (2*360/7 = 109,2857). Таким образом, в треугольнике не находится такой состав углов.
Как используют соотношение углов для нахождения треугольника?
Соотношение углов используется когда треугольник не находится в плоскости, что означает что нахождение подходящего треугольника зависит от других параметров. В этом случае значение углов будет различаться для разных физических ситуаций, которые включают трехмерность и так далее.
Как мы можем вычислить градусную меру большего из двух углов?
Чтобы вычислить градусную меру большего из двух углов мы можем предположить что углы есть X и 2X. Затем считаем их сумму используя ограничение – сумма двух углов = 183.857 градусов, складывая наше значение с константой 109.2857, мы получим значение 293.1427 градусов. Поскольку сумма углов в треугольнике должна быть 180 градусов, результат является некорректным, так как соотношение углов недопустимо для треугольника.
Частые источники ошибок при выполнении вычисления вокруг соотношения углов в треугольниках?
Ошибки частенько возникает из-за неправильного вычисления соотношения углов или неправильного получения точных угловка. Посчитать градусное измерение углов треугольников важно обратить внимание на то что сумма углов треугольника всегда равна 180 градусов, возможно делать вспомогательную выборку для большего уверенности.