Угловое расстояние это как найти

Угловое расстояние это как найти

В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла, концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера.

Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.

Использование[править | править код]

Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).

Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.

Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.

Измерение[править | править код]

Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).

Вычисление[править | править код]

Чтобы рассчитать угловое расстояние θ в угловых секундах для
двойной звёздные системы, экзопланеты, объекта Солнечной системы и других астрономических объектов, используется размер большой полуоси, выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках, согласно формуле для малых углов — {displaystyle tan({frac {a}{D}})}:

{displaystyle theta approx {dfrac {a}{D}}}

Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), {displaystyle alpha in [0,2pi ]} и склонением (dec), {displaystyle delta in [-pi /2,pi /2]} угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:

{displaystyle theta =cos ^{-1}left[sin(delta _{1})sin(delta _{2})+cos(delta _{1})cos(delta _{2})cos(alpha _{1}-alpha _{2})right]}

См. также[править | править код]

  • Тысячная
  • Град, минута, секунда
  • Часовой угол
  • Центральный угол
  • Угловой размер
  • Угловое смещение
  • Ортодромия

Литература[править | править код]

  • Климишин И. А. Астрономия наших дней. — Рипол Классик, 1980. — С. 99. — 561 с.
  • Weisstein, Eric W. Angular Distance (англ.). — MathWorld.
Источник

From Wikipedia, the free encyclopedia

Angular distance or angular separation, also known as apparent distance or apparent separation, denoted theta , is the angle between the two sightlines, or between two point objects as viewed from an observer.

Angular distance appears in mathematics (in particular geometry and trigonometry) and all natural sciences (e.g.,kinematics astronomy and geophysics). In the classical mechanics of rotating objects, it appears alongside angular velocity, angular acceleration, angular momentum, moment of inertia and torque.

Use[edit]

The term angular distance (or separation) is technically synonymous with angle itself, but is meant to suggest the linear distance between objects (for instance, a couple of stars observed from Earth).

Measurement[edit]

Since the angular distance (or separation) is conceptually identical to an angle, it is measured in the same units, such as degrees or radians, using instruments such as goniometers or optical instruments specially designed to point in well-defined directions and record the corresponding angles (such as telescopes).

Equation[edit]

General case[edit]

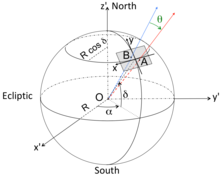
Angular separation theta between points A and B as seen from O

To derive the equation that describes the angular separation of two points located on the surface of a sphere as seen from the center of the sphere, we use the example of two astronomical objects A and B observed from the Earth. The objects A and B are defined by their celestial coordinates, namely their right ascensions (RA), {displaystyle (alpha _{A},alpha _{B})in [0,2pi ]}; and declinations (dec), {displaystyle (delta _{A},delta _{B})in [-pi /2,pi /2]}. Let O indicate the observer on Earth, assumed to be located at the center of the celestial sphere. The dot product of the vectors {displaystyle mathbf {OA} } and {displaystyle mathbf {OB} } is equal to:

{displaystyle mathbf {OA} cdot mathbf {OB} =R^{2}cos theta }

which is equivalent to:

{displaystyle mathbf {n_{A}} .mathbf {n_{B}} =cos theta }

In the (x,y,z) frame, the two unitary vectors are decomposed into:

{displaystyle mathbf {n_{A}} ={begin{pmatrix}cos delta _{A}cos alpha _{A}\cos delta _{A}sin alpha _{A}\sin delta _{A}end{pmatrix}}mathrm {qquad andqquad } mathbf {n_{B}} ={begin{pmatrix}cos delta _{B}cos alpha _{B}\cos delta _{B}sin alpha _{B}\sin delta _{B}end{pmatrix}}.}

Therefore,

{displaystyle mathbf {n_{A}} mathbf {n_{B}} =cos delta _{A}cos alpha _{A}cos delta _{B}cos alpha _{B}+cos delta _{A}sin alpha _{A}cos delta _{B}sin alpha _{B}+sin delta _{A}sin delta _{B}equiv cos theta }

then:

{displaystyle theta =cos ^{-1}left[sin delta _{A}sin delta _{B}+cos delta _{A}cos delta _{B}cos(alpha _{A}-alpha _{B})right]}

Small angular distance approximation[edit]

The above expression is valid for any position of A and B on the sphere. In astronomy, it often happens that the considered objects are really close in the sky: stars in a telescope field of view, binary stars, the satellites of the giant planets of the solar system, etc. In the case where {displaystyle theta ll 1} radian, implying {displaystyle alpha _{A}-alpha _{B}ll 1} and {displaystyle delta _{A}-delta _{B}ll 1}, we can develop the above expression and simplify it. In the small-angle approximation, at second order, the above expression becomes:

{displaystyle cos theta approx 1-{frac {theta ^{2}}{2}}approx sin delta _{A}sin delta _{B}+cos delta _{A}cos delta _{B}left[1-{frac {(alpha _{A}-alpha _{B})^{2}}{2}}right]}

meaning

{displaystyle 1-{frac {theta ^{2}}{2}}approx cos(delta _{A}-delta _{B})-cos delta _{A}cos delta _{B}{frac {(alpha _{A}-alpha _{B})^{2}}{2}}}

hence

{displaystyle 1-{frac {theta ^{2}}{2}}approx 1-{frac {(delta _{A}-delta _{B})^{2}}{2}}-cos delta _{A}cos delta _{B}{frac {(alpha _{A}-alpha _{B})^{2}}{2}}}.

Given that {displaystyle delta _{A}-delta _{B}ll 1} and {displaystyle alpha _{A}-alpha _{B}ll 1}, at a second-order development it turns that {displaystyle cos delta _{A}cos delta _{B}{frac {(alpha _{A}-alpha _{B})^{2}}{2}}approx cos ^{2}delta _{A}{frac {(alpha _{A}-alpha _{B})^{2}}{2}}}, so that

{displaystyle theta approx {sqrt {left[(alpha _{A}-alpha _{B})cos delta _{A}right]^{2}+(delta _{A}-delta _{B})^{2}}}}

Small angular distance: planar approximation[edit]

Planar approximation of angular distance on sky

If we consider a detector imaging a small sky field (dimension much less than one radian) with the y-axis pointing up, parallel to the meridian of right ascension alpha , and the x-axis along the parallel of declination delta , the angular separation can be written as:

{displaystyle theta approx {sqrt {delta x^{2}+delta y^{2}}}}

where {displaystyle delta x=(alpha _{A}-alpha _{B})cos delta _{A}} and {displaystyle delta y=delta _{A}-delta _{B}}.

Note that the y-axis is equal to the declination, whereas the x-axis is the right ascension modulated by {displaystyle cos delta _{A}} because the section of a sphere of radius R at declination (latitude) delta is {displaystyle R'=Rcos delta _{A}} (see Figure).

See also[edit]

  • Milliradian
  • Gradian
  • Hour angle
  • Central angle
  • Angle of rotation
  • Angular diameter
  • Angular displacement
  • Great-circle distance
  • Cosine similarity § Angular distance and similarity

References[edit]

  • CASTOR, author(s) unknown. “The Spherical Trigonometry vs. Vector Analysis”.
  • Weisstein, Eric W. “Angular Distance”. MathWorld.
Источник

Содержание

  1. Как найти угловое расстояние в астрономии: формула
  2. Что такое угловое расстояние?
  3. Формула для расчета углового расстояния
  4. Пример расчета углового расстояния
  5. Выводы
  6. Как найти угловое расстояние в астрономии: формула и применение
  7. Что такое угловое расстояние?
  8. Как найти угловое расстояние?
  9. Применение углового расстояния
  10. Вывод
  11. Как найти угловое расстояние астрономия формула
  12. Формула для нахождения углового расстояния
  13. Пример использования формулы углового расстояния
  14. Заключение

Как найти угловое расстояние в астрономии: формула

В астрономии угловое расстояние используется для измерения углов между небесными телами. Это понятие может показаться сложным для новичков в науке, но на самом деле оно является основополагающим для понимания многих астрономических процессов.

Что такое угловое расстояние?

Угловое расстояние — это угол, отмеряемый между двумя линиями зрения из наблюдаемой точки наблюдения. В астрономии это часто используется для измерения углов между небесными телами. На основе углового расстояния можно рассчитать дистанцию между объектами на небесной сфере.

Угловое расстояние может быть выражено в различных единицах измерения, таких как градусы, минуты и секунды дуги, радианы и т.д. В астрономии чаще всего используют градусы.

Формула для расчета углового расстояния

Формула для расчета углового расстояния в астрономии выглядит следующим образом:

Угол = arccos(sin(δ1)sin(δ2) + cos(δ1)cos(δ2)cos(α1-α2))

где:

  • δ1, δ2 — сферические координаты широты небесных тел
  • α1, α2 — сферические координаты долготы небесных тел

Данная формула может быть использована для расчета углового расстояния между любыми двумя небесными телами в небесной сфере.

Пример расчета углового расстояния

Рассмотрим пример расчета углового расстояния между двумя звездами с известными координатами:

  • Звезда 1: α = 5 ч 34 мин, δ = -5 град
  • Звезда 2: α = 5 ч 32 мин, δ = -4 град 30 мин

Сначала необходимо перевести сферические координаты в радианы:

  • Звезда 1: α = 5.567 рад, δ = -0.087 рад
  • Звезда 2: α = 5.527 рад, δ = -0.079 рад

После чего применяем формулу:

Угол = arccos(sin(-0.087)sin(-0.079) + cos(-0.087)cos(-0.079)cos(5.567-5.527)) ≈ 1.156 град

Таким образом, угловое расстояние между этими звездами составляет 1.156 град.

Выводы

Угловое расстояние — это важное понятие в астрономии для измерения углов между небесными телами и расчета дистанций на небесной сфере. Формула для расчета углового расстояния может быть использована для любых двух небесных тел с известными сферическими координатами. Понимание этого понятия является необходимым для дальнейшего изучения астрономии и понимания ее процессов.

Как найти угловое расстояние в астрономии: формула и применение

Астрономия — это наука, которая изучает объекты, находящиеся за пределами нашей планеты, в том числе звезды, планеты, галактики и другие космические объекты. В астрономии угловое расстояние является важным показателем для определения расстояний и движений объектов в космосе. В этой статье мы рассмотрим, как найти угловое расстояние астрономии формула и как ее применить для решения различных задач.

Что такое угловое расстояние?

Угловое расстояние — это угол между двумя объектами на небосводе, измеряемый в градусах, минутах и секундах дуги. В астрономии угловое расстояние используется для измерения расстояний между звездами, планетами, галактиками и другими космическими объектами.

Как найти угловое расстояние?

Для нахождения углового расстояния необходимо знать координаты объектов на небосводе. Координаты можно выразить в градусах, минутах и секундах дуги или в радианах.

Существует несколько способов нахождения углового расстояния. Один из них использует формулу косинуса.

cos(d) = sin(δ1) x sin(δ2) + cos(δ1) x cos(δ2) x cos(α1-α2)

где d — угловое расстояние, δ1 и δ2 — склонения объектов, α1 и α2 — прям ascensions объектов.

С помощью этой формулы можно вычислить угловое расстояние между любыми двумя объектами на небосводе.

Применение углового расстояния

Угловое расстояние имеет множество применений в астрономии. Например, с его помощью можно измерять расстояния между звездами и планетами, определять скорости и направления их движения, исследовать структуру галактик и многое другое.

Кроме того, угловое расстояние является важным параметром в навигации космических аппаратов. Оно помогает определять положение аппаратов на орбите и контролировать их движение.

Вывод

Угловое расстояние является важным показателем в астрономии, который используется для решения различных задач, связанных с изучением космических объектов и навигацией космических аппаратов. Для нахождения углового расстояния можно использовать формулу косинуса, которая позволяет рассчитать расстояние между любыми двумя объектами на небосводе.

  • Ключевые слова: астрономия, угловое расстояние, формула, применение.
  • Связанные темы: космос, звезды, планеты, галактики, навигация космических аппаратов.

Как найти угловое расстояние астрономия формула

В астрономии угловое расстояние — это угол между двумя точками на небесной сфере. Несмотря на то, что это понятие может показаться довольно абстрактным, оно очень важно для астрономов.

Формула для нахождения углового расстояния

Для нахождения углового расстояния между двумя небесными объектами используется следующая формула:

cos(d) = sin(δ1)sin(δ2) + cos(δ1)cos(δ2)cos(α1 — α2)

Здесь δ1 и δ2 — это прямые восхождения двух объектов, α1 и α2 — их наклонения, а d — искомый угол между ними.

Чтобы решить эту формулу, нужно знать координаты двух небесных объектов. Эти координаты могут быть найдены с помощью астрономической программы или каталога звезд, таких как SIMBAD.

Пример использования формулы углового расстояния

Давайте рассмотрим пример, чтобы увидеть, как использовать формулу для нахождения углового расстояния между двумя небесными объектами.

Предположим, что мы хотим найти угловое расстояние между звездой Сириус и планетой Марс. Мы можем использовать значения их координат для решения нашей формулы.

Для Сириуса:

  • Прямое восхождение (δ) = 101,287155 градусов
  • Наклонение (α) = -16,716115 градусов

Для Марса:

  • Прямое восхождение (δ) = 331,403594 градусов
  • Наклонение (α) = 1,849726 градусов

Теперь, зная эти значения, мы можем подставить их в нашу формулу для нахождения углового расстояния:

cos(d) = sin(16,716115)sin(1,849726) + cos(16,716115)cos(1,849726)cos(331,403594 — 101,287155)

cos(d) = 0,194937

Теперь, чтобы найти угловое расстояние (d), нам нужно взять обратный косинус от 0,194937:

d = cos-1(0,194937)

d = 78,682°

Таким образом, угол между звездой Сириус и планетой Марс составляет 78,682°.

Заключение

Угловое расстояние — это важное понятие в астрономии, используемое для измерения угла между двумя точками на небесной сфере. Формула для нахождения углового расстояния, которую мы рассмотрели в этой статье, позволяет решать эту задачу с высокой точностью. Зная координаты двух небесных объектов, вы можете легко рассчитать угловое расстояние между ними при помощи этой формулы.

Источник

В презентации кратко описаны способы определения углового расстояния между астрономическими объектами – как теоретически обоснованные и общепринятые, так и “народные”.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Слайд 1

Способы определения углового расстояния между астрономическими объектами. Выполнил воспитанник 11 А : Захаров Алексей Евгеньевич Преподаватель: Богданенко Елена Николаевна ГБОУ РО «НШИ с ПЛП» Таганрог, 2020

Слайд 2

Угловое расстояние Угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов.

Слайд 3

Определение угловых размеров на небе с помощью руки Для того чтобы научиться искать созвездия на ночном небе, для начала, достаточно знать древнейший астеризм “Большой Ковш” – его семь звезд, самых ярких в созвездии Большая Медведица, являются направляющими (путеводными) для поиска звезд в других созвездиях. На примере астеризма Ковш созвездия Большая Медведица показаны угловые расстояния между звёздами, а также схематически вытянутая рука и расстояние между пальцами. Например, «ширина» мизинца равна 1°, кулак — 10°, «коза» с большим пальцем — 20°.

Слайд 4

Вариант с 3 — 4 — 6° выглядит очень любопытно. Во-первых, позволяет определить расстояние между объектами, которые лежат не на одной линии, а во-вторых, косточки указательного пальца так же могут выступать в качестве линейки. Ещё один вариант определения углового размера.

Слайд 5

Как найти созвездие Малая Медведица Поиск созвездия Малой Медведицы обычно все начинают с поиска Полярной Звезды , чтобы найти Полярную Звезду нужно мысленно провести линию между звездами края Ковша от Мерак к Дубхе и продолжить до первой яркой звезды – это и будет Полярная Звезда, указывающая направление на Север! Полярная Звезда является важнейшей навигационной звездой, а Мерак и Дубхе , помогающие ее найти, еще называют Указателями.

Слайд 6

Как найти созвездие Кассиопея Всесезонный способ определения местоположения Кассиопеи, заключается в “нацеливании” луча, через уже известные звезды. Самый лучший “выстрел” получится если продолжить линию от Алиот (ε UMa ) за Полярную Звезду (α UMa ) при этом получится точное попадание в Гамма Кассиопеи Нави (γ Cas ), к тому же приглядевшись, Вы обнаружите, что Большой Ковш и астеризм Трон Кассиопеи расположены центрально-симметрично относительно Полярной Звезды.

Слайд 7

Расчет углового расстояния между двумя астрономическими объектами Во второй экваториальной системе координат положение объектов определяется двумя угловыми параметрами, называемыми прямое восхождение α и склонение δ. β – это угловое расстояние между двумя небесными объектами, α 1 и δ 1 , прямое восхождение и склонение, характеризующие положение Объекта 1 на небесной сфере, соответственно, положение Объекта 2 характеризуется α 2 и δ 2 . Склонение определяется величиной угла от линии небесного экватора до объекта в плоскости перпендикулярной экватору. Прямое восхождение определяется величиной угла между точкой весеннего равноденствия и точкой отсчета склонения. Важно запомнить, что прямое восхождение отсчитывается от точки весеннего равноденствия в направлении противоположном движению часовой стрелки (в точке весеннего равноденствия Солнце вступает в знак Овна) и его величина выражается не градусах, а в часах .

Слайд 8

Расчет углового расстояния между двумя астрономическими объектами, положение которых определено во второй экваториальной системе координат На рисунке величина α 1 примерно составляет 1 час, а α 2 достигает величины почти в 18 часов и соответствующая дуга охватывает три четверти длины линии небесного экватора. Формула расчета углового расстояния выводится с помощью тригонометрических преобразований угловых параметров треугольников соединяющих точки, соответствующие положению объектов на небесной сфере, центр этой сферы и точки отсчета склонений объектов : β = arccos ( sin (δ 1 )* sin (δ 2 )+ cos (δ 1 )* cos (δ 2 )* cos (α 1 – α 2 )) ,

Слайд 9

Список используемых источников: 1) https://ru.wikipedia.org/wiki/%D0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D0%B5 2) https://2i.by/opredelenie-razmerov/ 3) http://www.abc2home.ru/znaki_zodiaka/sozvezdiya/kak_nayti_sozvezdie.html#gruppa_bolshaya_medvedica 4) http://www.abc2home.ru/blog/uglovoye_rasstoyanie_mezhdu_zvyozdami.html

Слайд 10

Спасибо за внимание !

Источник

В математике (в частности, геометрия и тригонометрия ) и все естественные науки (например, астрономия и геофизика ), угловое расстояние (также известное как угловое разделение, видимое расстояние или видимое разделение ) между двумя точечными объектами, если смотреть с места, отличного от любого из этих объектов, составляет угол длины между двумя направлениями, исходящими от наблюдателя и указывающими на эти два объекта.

Угловое расстояние проявляется в классической механике вращающихся объектов наряду с угловой скоростью, угловым ускорением, угловым моментом, момент инерции и крутящий момент.

Содержание

  • 1 Использование
  • 2 Измерение
  • 3 Уравнение
  • 4 См. Также
  • 5 Справочные материалы

Использование

Термин угловое расстояние (или разделение) технически является синонимом самого угла, но предназначен для обозначения (часто обширного, неизвестного или несущественного) линейного расстояния между этими объектами (например, звезды, наблюдаемые с Земли ).

Измерение

Поскольку угловое расстояние (или разделение) концептуально идентично углу, оно измеряется в тех же единицах, например, градусов или радианы с использованием таких инструментов, как гониометры или оптических инструментов, специально разработанных для указания в четко определенных направлениях и записи соответствующих углов (например, телескопов ).

Уравнение

Для вычисления углового расстояния θ { displaystyle theta} theta в угловых секундах для двойной звезды систем, внесолнечных планет, объектов солнечной системы и других астрономических объектов, мы используем орбитальное расстояние (полу- большая ось ), a { displaystyle a}a , в AU, деленное на расстояние до звезды D { displaystyle D}D в парсеках, в соответствии с приближением малого угла для tan ⁡ (a D) { displaystyle tan left ({ frac {a} {D}} справа)}{ displaystyle tan left ({ frac {a} {D}} right)} :

θ ≈ a D { displaystyle theta приблизительно { dfrac {a} {D}}} theta приблизительно { dfrac aD}

Даны два угловых положения, каждое из которых определяется как прямое восхождение (RA), α ∈ [0, 2 π] { Displaystyle альфа в [0,2 pi]}{ displaystyle alpha in [0, 2 pi]} ; и склонение (уб), δ ∈ [- π / 2, π / 2] { displaystyle delta in [- pi / 2, pi / 2]}{ displaystyle delta in [- pi / 2, pi / 2]} , угловое расстояние между двумя точками можно рассчитать как,

θ = cos – 1 ⁡ [sin ⁡ (δ 1) sin ⁡ (δ 2) + cos ⁡ (δ 1) cos ⁡ (δ 2) соз ⁡ (α 1 – α 2)] { displaystyle theta = cos ^ {- 1} left [ sin ( delta _ {1}) sin ( delta _ {2}) + cos ( delta _ {1}) cos ( delta _ {2}) cos ( alpha _ {1} – alpha _ {2}) right]}{ displaystyle theta = cos ^ {- 1} left [ sin ( delta _ {1}) sin ( delta _ {2}) + cos ( delta _ {1}) cos ( delta _ {2}) cos ( alpha _ {1} - alpha _ {2}) right]}

См. также

  • Миллирадиан
  • Градиан
  • Часовой угол
  • Центральный угол
  • Угловой диаметр
  • Угловое смещение
  • Расстояние по большому кругу
  • Косинусное сходство # Угловое расстояние и подобие

Литература

  • КАСТОР, автор ( с) неизвестно. «Сферическая тригонометрия и векторный анализ».
  • Вайсштейн, Эрик У. «Угловое расстояние». MathWorld.
Источник

Добавить комментарий