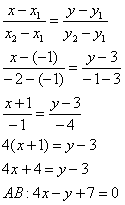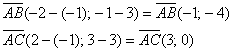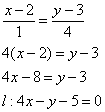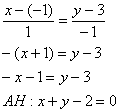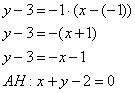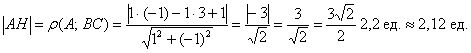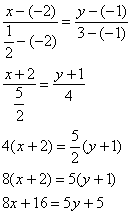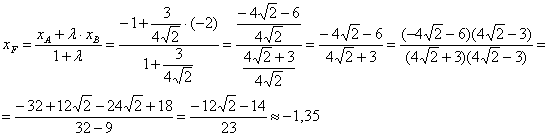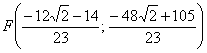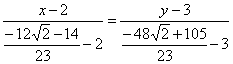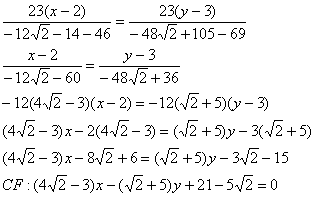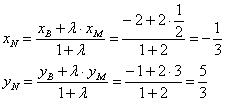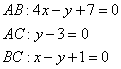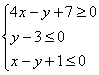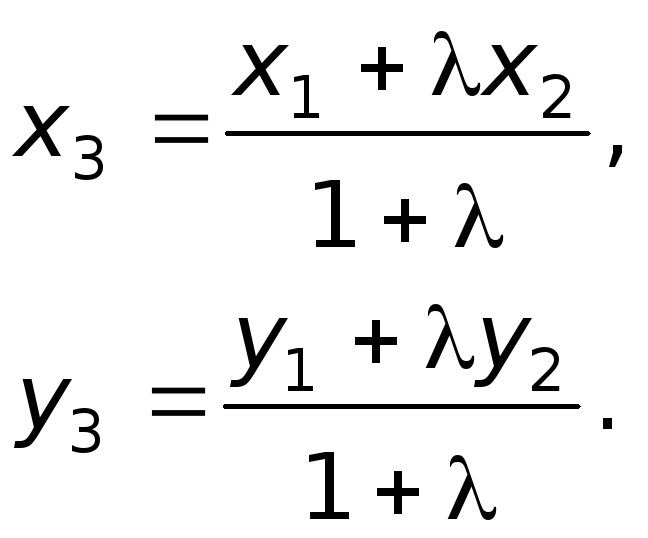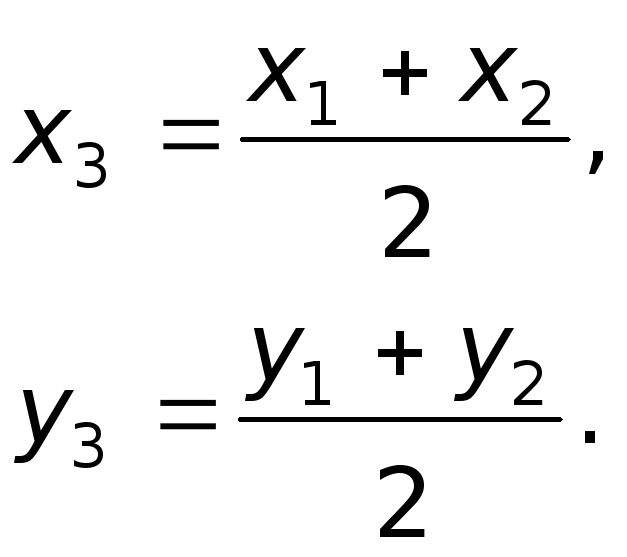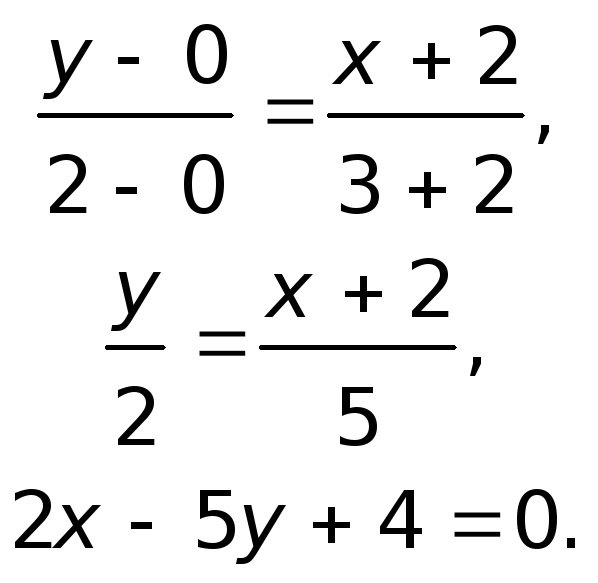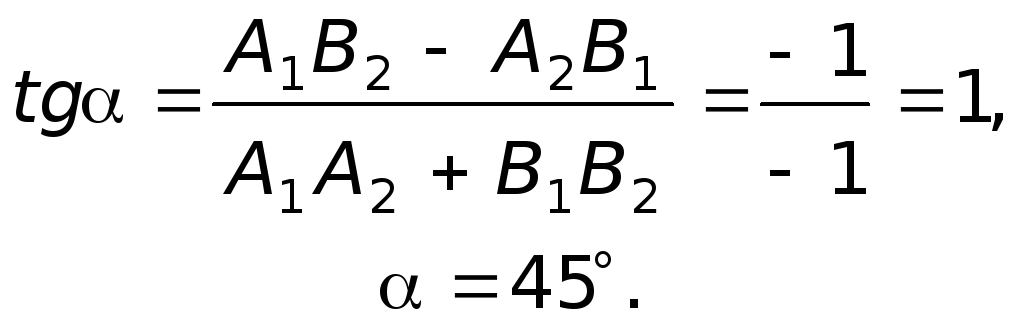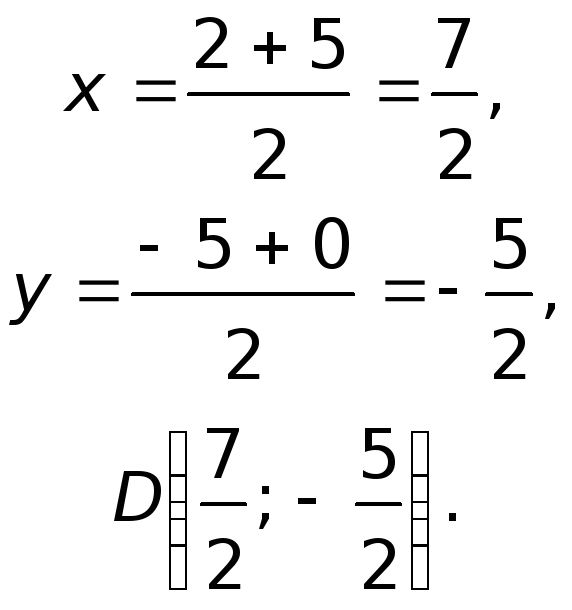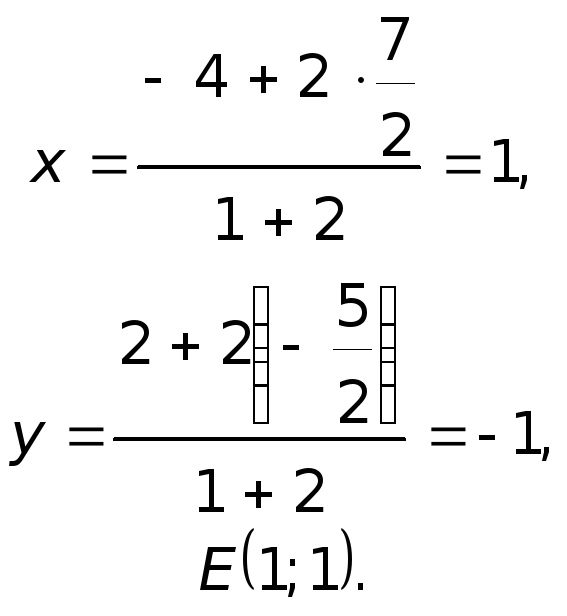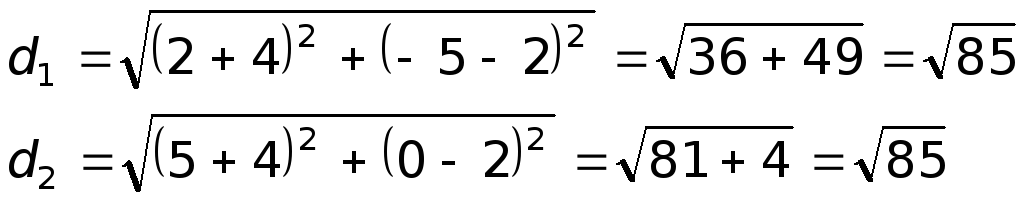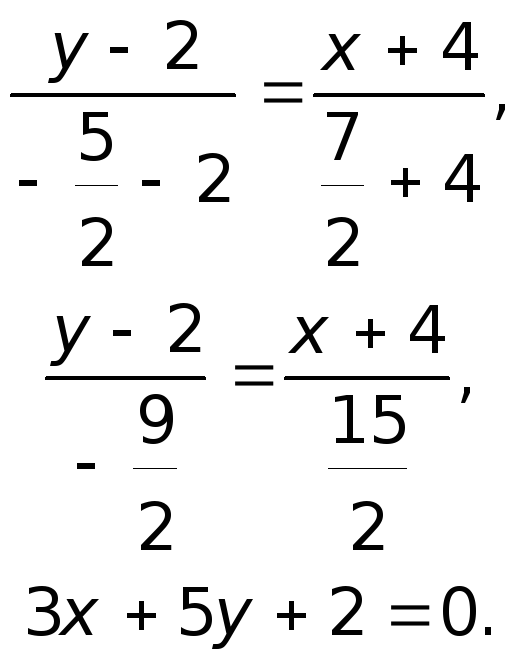Угловой коэффициент стороны треугольника как его найти - Сайт, где вы сможете решить свои вопросы

Тема: Как вычеслить угловой коэффициент стороны треугольника ? Уравнение стороны нашел (Прочитано 9466 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Уравнение стороны треугольника : 3x-4y+8=0.
помогите пожалуйста с угловым коэффициентом , какего вычеслить ( то что он вычесляется по формуле: у= кх+в я знаю но не получается у меня со знаками путаюсь )

выразите из вашего уравнения y

Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….

Уравнение стороны треугольника : 3x-4y+8=0.
помогите пожалуйста с угловым коэффициентом , какего вычеслить ( то что он вычесляется по формуле: у= кх+в я знаю но не получается у меня со знаками путаюсь )

Есл имеется общее уравнение прямой ( Ax+By+C=0 ) (как у вас), то угловой коэффициент равен ( k=-frac{A}{B} ) либо

выразите из вашего уравнения y

т.е. сведите его к виду

то что он вычесляется по формуле: у= кх+в я знаю

А коэффициент “С” куда пропадет ?
ребят помогите решением пожалуйста . для наглядности

выразите из вашего уравнения y

А коэффициент “С” куда пропадет ?

никуда не пропадет, просто он никак не влияет на угловой коэффициент прямой

x+y+3=0 => y=-x-3 => k=-1

Источник

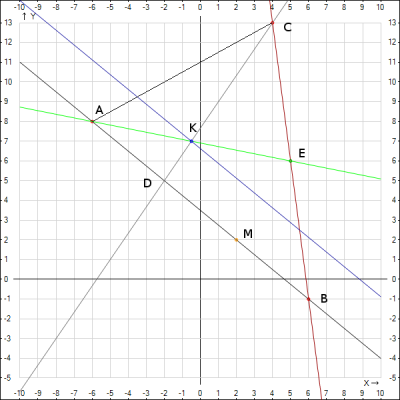
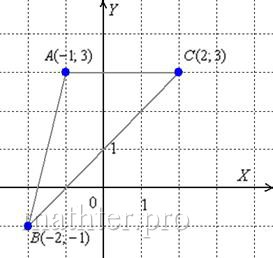
1. Уравнение сторон АВ и ВС и их угловые коэффициенты.
В задании даны координаты точек, через которые проходят эти прямые, поэтому воспользуемся уравнением прямой, проходящей через две заданные точки $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$ подставляем и получаем уравнения
уравнение прямой AB $$frac{x+6}{6+6}=frac{y-8}{-1-8} => y = -frac{3}{4}x + frac{7}{2}$$ угловой коэффициент прямой AB равен (k_{AB} = -frac{3}{4})
уравнение прямой BC $$frac{x-4}{6-4}=frac{y-13}{-1-13} => y = -7x + 41$$ угловой коэффициент прямой BC равен (k_{BC} = -7)

2. Угол В в радианах с точностью до двух знаков
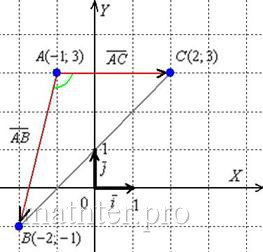
Угол B – угол между прямыми AB и BC, который рассчитывается по формуле $$tgphi=|frac{k_2-k_1}{1+k_2*k_1}|$$подставляем значения угловых коэффициентов этих прямых и получаем $$tgphi=|frac{-7+frac{3}{4}}{1+7*frac{3}{4}}| = 1 => phi = frac{pi}{4} approx 0.79$$
3.Длину стороны АВ
Длина стороны AB рассчитывается как расстояние между точками и равна (d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2}) => $$d_{AB} = sqrt{(6+6)^2+(-1-8)^2} = 15$$
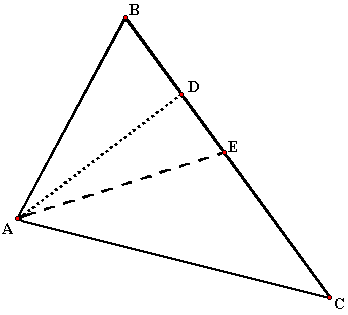
4.Уравнение высоты CD и ее длину.
Уравнение высоты будем находить по формуле прямой проходящей через заданную точку С(4;13) в заданном направлении – перпендикулярно прямой AB по формуле (y-y_0=k(x-x_0)). Найдем угловой коэффициент высоты (k_{CD}) воспользовавшись свойством перпендикулярных прямых (k_1=-frac{1}{k_2}) получим $$k_{CD}= -frac{1}{k_{AB}} = -frac{1}{-frac{3}{4}} = frac{4}{3}$$ Подставляем в уравнение прямой, получаем $$y – 13 = frac{4}{3}(x-4) => y = frac{4}{3}x+frac{23}{3}$$ Длину высоты будем искать как расстояние от точки С(4;13) до прямой AB по формуле $$d = frac{Ax_0+By_0+C}{sqrt{A^2+B^2}}$$ в числителе уравнение прямой AB, приведем его к этому виду (y = -frac{3}{4}x + frac{7}{2} => 4y+3x-14 = 0) , подставляем полученное уравнение и координаты точки в формулу $$d = frac{4*13+3*4-14 }{sqrt{4^2+3^2}} = frac{50}{5} =10$$

5. Уравнение медианы АЕ и координаты точки К пересечение этой медианы с высотой CD.
Уравнение медианы будем искать как уравнение прямой, проходящей через две заданные точки А(-6;8) и E , где точка E – середина между точками B и C и ее координаты находятся по формуле (E(frac{x_2+x_1}{2};frac{y_2+y_1}{2})) подставляем координаты точек (E(frac{6+4}{2};frac{-1+13}{2})) => (E(5; 6)), тогда уравнение медианы AE буде следующее $$frac{x+6}{5+6}=frac{y-8}{6-8} => y = -frac{2}{11}x + frac{76}{11}$$Найдем координаты точки пересечения высот и медианы, т.е. найдем их общую точку Для этого составим систему уравнение $$begin{cases}y = -frac{2}{11}x + frac{76}{11}\y = frac{4}{3}x+frac{23}{3}end{cases}=>begin{cases}11y = -2x +76\3y = 4x+23end{cases}=>$$$$begin{cases}22y = -4x +152\3y = 4x+23end{cases}=> begin{cases}25y =175\3y = 4x+23end{cases}=> $$$$begin{cases}y =7\ x=-frac{1}{2}end{cases}$$ Координаты точки пересечения (K(-frac{1}{2};7))

6.Уравнение прямой что проходит через точку К параллельно к стороне АВ.
Если прямая параллельны, то их угловые коэффициенты равны, т.е. (k_{AB}=k_{K} = -frac{3}{4}) , также известны координаты точки (K(-frac{1}{2};7)), т.е. для нахождения уравнения прямой применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении (y – y_0=k(x-x_0)), подставляем данные и получаем $$y – 7= -frac{3}{4}(x-frac{1}{2}) => y = -frac{3}{4}x + frac{53}{8}$$

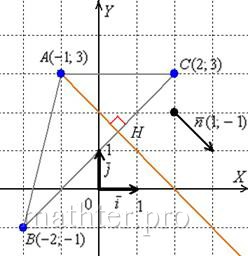
8. Координаты точки М которая симметрична точке А относительно прямой CD.
Точка M лежит на прямой AB, т.к. CD – высота к этой стороне. Найдем точку пересечения CD и AB для этого решим систему уравнений $$begin{cases}y = frac{4}{3}x+frac{23}{3}\y = -frac{3}{4}x + frac{7}{2}end{cases} =>begin{cases}3y = 4x+23\4y =-3x + 14end{cases} => $$$$begin{cases}12y = 16x+92\12y =-9x + 42end{cases} =>
begin{cases}0= 25x+50\12y =-9x + 42end{cases} => $$$$begin{cases}x=-2\y=5 end{cases}$$ Координаты точки D(-2;5). По условию AD=DK, это расстояние между точками находится по формуле Пифагора (d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2}), где AD и DK – гипотенузы равных прямоугольных треугольников, а (Δx =x_2-x_1) и (Δy=y_2-y_1) – катеты этих треугольников, т.е. найдем катеты найдем и координаты точки M. (Δx=x_D-x_A = -2+6=4), а (Δy=y_D-y_A = 5-8=-3), тогда координаты точки M будут равны (x_M-x_D = Δx => x_D +Δx =-2+4=2 ), а (y_M-y_D = Δy => y_D +Δy =5-3=2 ), получили, что координаты точки (M(2;2))

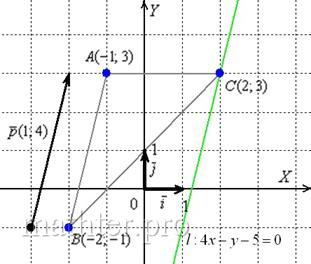
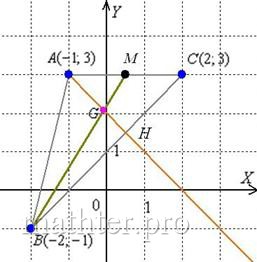
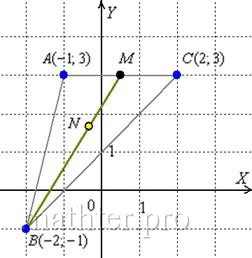
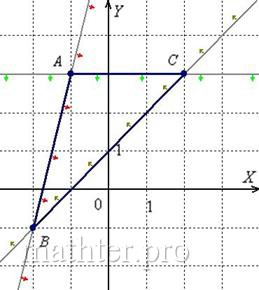
9. Нанесем точки и прямые на декартовую систему координат

Источник

Загрузить PDF

Угловой коэффициент характеризует угол наклона прямой к оси абсцисс (угловой коэффициент численно равен тангенсу этого угла). Угловой коэффициент присутствует в уравнении прямой и используется в математическом анализе кривых, где всегда равен производной функции. Для облегчения понимания углового коэффициента представьте, что он влияет на скорость изменения функции, то есть чем больше значение углового коэффициента, тем больше значение функции (при одном и том же значении независимой переменной).

1

Используйте угловой коэффициент для нахождения угла наклона прямой к оси абсцисс и направления этой прямой. Вычислить угловой коэффициент довольно легко, если вам дано уравнение прямой. Запомните, что в любом уравнении прямой:
2

Для нахождения углового коэффициента необходимо найти значение k (коэффициент при «х»). Если данное вам уравнение имеет вид , то для нахождения углового коэффициента вам нужно просто посмотреть на число, стоящее перед «х». Обратите внимание, что k (угловой коэффициент) всегда находится при независимой переменной (в данном случае «х»). Если вы запутались, просмотрите следующие примеры:
3

Если данное вам уравнение имеет вид, отличный от , обособьте зависимую переменную. В большинстве случаев зависимая переменная обозначается как «у», а для ее обособления можно выполнять операции сложения, вычитания, умножения и другие. Помните, что любая математическая операция должна быть выполнена на обеих сторонах уравнения (чтобы не менять его исходного значения). Вам необходимо привести любое данное вам уравнение к виду . Рассмотрим пример:

Реклама

1
Для вычисления углового коэффициента воспользуйтесь графиком и двумя точками. Если вам дан просто график функции (без уравнения), вы все еще можете найти угловой коэффициент. Для этого вам понадобятся координаты любых двух точек, лежащих на этом графике; координаты подставляются в формулу: ${frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Чтобы избежать ошибок при вычислении углового коэффициента, запомните следующее:
- Если график возрастает, то угловой коэффициент имеет положительное значение.
- Если график убывает, то угловой коэффициент имеет отрицательное значение.
- Чем больше значение углового коэффициента, тем круче график (и наоборот).
- Угловой коэффициент прямой, параллельной оси абсцисс, равен 0.
- Угловой коэффициент прямой, параллельной оси ординат, не существует (он бесконечен).^[4]
2
Найдите координаты двух точек. На графике отметьте любые две точки и найдите их координаты (х,у). Например, на графике лежат точки А(2,4) и В(6,6).^[5]
- В паре координат первое число соответствует «х», а второе – «у».
- Каждому значению «х» соответствует определенное значение «у».
3
Приравняйте x₁, y₁, x₂, y₂ к соответствующим значениям. В нашем примере с точками А(2,4) и В(6,6):
- x₁: 2
- y₁: 4
- x₂: 6
- y₂: 6^[6]
4

Подставьте найденные значения в формулу для вычисления углового коэффициента. Чтобы найти угловой коэффициент, используются координаты двух точек и следующая формула: ${frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Подставьте в нее координаты двух точек.
5

Объяснение сути формулы. Угловой коэффициент равен отношению изменения координаты «у» (двух точек) к изменению координаты «х» (двух точек). Изменение координаты – это разность между значениями соответствующей координаты первой и второй точек.
6

Другой вид формулы для вычисления углового коэффициента. Стандартная формула для вычисления углового коэффициента: k = ${frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Но она может иметь следующий вид: k = Δy/Δx, где Δ – это греческая буква «дельта», обозначающая в математике разность. То есть, Δx = x_2 – x_1, а Δy = y_2 – y_1.^[8]

Реклама

1
Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.
- Прочитайте статью Как брать производную.
- Как брать простейшие производные, например, производную показательного уравнения, описано этой статье. Вычисления, представленные в следующих шагах, будут основаны на описанных в ней методах.
2

Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции. В задачах не всегда предлагается найти угловой коэффициент или производную функции. Например, вас могут попросить найти скорость изменения функции в точке А(х,у). Также вас могут попросить найти угловой коэффициент касательной в точке А(х,у). В обоих случаях необходимо брать производную функции.
3
Возьмите производную данной вам функции. Здесь строить график не нужно – вам понадобится только уравнение функции. В нашем примере возьмите производную функции $f(x)=2x^{2}+6x$ . Берите производную согласно методам, изложенным в упомянутой выше статье:
- Производная:
4

В найденную производную подставьте координаты данной вам точки, чтобы вычислить угловой коэффициент. Производная функции равна угловому коэффициенту в определенной точке. Другими словами, f'(х) – это угловой коэффициент функции в любой точке (x,f(x)). В нашем примере:
5
Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.
- Касательная будет иметь тот же угловой коэффициент, что и график функции в определенной точке. Для того, чтобы провести касательную в данной точке, двигайтесь вправо/влево по оси Х (в нашем примере на 22 значения вправо), а затем вверх на единицу по оси Y. Отметьте точку, а затем соедините ее с данной вам точкой. В нашем примере соедините точки с координатами (4,2) и (26,3).
Реклама

Об этой статье

Эту страницу просматривали 143 640 раз.

Была ли эта статья полезной?

Источник

2.9. Типовая задача с треугольником

Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в

сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не

будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны.

Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется

найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё:

Задача 95

Даны вершины треугольника . Требуется:

1) составить уравнения сторон и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить прямой , проходящей через точку параллельно прямой ;
5) составить уравнение высоты и найти её длину;
6) вычислить площадь треугольника ;
7) составить уравнение медианы ;
8) найти точку пересечения .
и для особо опасных энтузиастов:
9) найти уравнение биссектрисы ;
10) найти центр тяжести треугольника;
11) составить систему линейных неравенств, определяющих треугольник.

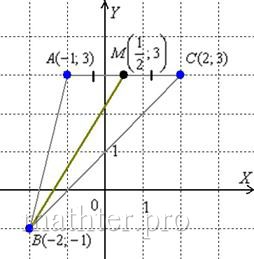
С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и

самопроверки всегда строим чертёж на черновике, не устану это рекомендовать:

Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1

см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой.

Вперёд без страха и сомнений:

1) Составим уравнения сторон и найдём их угловые

коэффициенты.
Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум

точкам.

Составим уравнение стороны по точкам :

Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение.

Теперь

найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

Таким образом, угловой коэффициент:

Самостоятельно разбираемся со сторонами и сверяемся, что

получилось:

2) Найдём длину стороны . Используем соответствующую формулу для точек :

Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка 🙂

3) Найдём . Это Задача 31, повторим:

Используем формулу .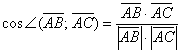
Найдём векторы:

Таким образом:
, и сам угол:
, ну что же, похоже на правду, желающие могут приложить транспортир, у кого

он есть.

Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла

между прямыми, так как они всегда дают острый угол.

4) Составим уравнение прямой , проходящей через точку параллельно прямой . Это стандартная задача, и мы ленимся отработать её вновь!

Из общего уравнения прямой вытащим направляющий вектор .

Составим уравнение прямой по точке и направляющему вектору :

5) Составим уравнение высоты и найдём её длину.
Первую часть задания мы тоже решали:

Из уравнения стороны снимаем вектор нормали . Уравнение высоты

составим по точке и направляющему вектору :

Обратите внимание, что координаты точки нам не известны.

Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: . В данном случае , тогда: . Уравнение высоты составим по точке и угловому коэффициенту :

Длину высоты можно найти двумя способами.

Существует окольный путь:

а) находим – точку

пересечения высоты и стороны ;

б) находим длину отрезка по двум

известным точкам.

Но зачем? – ведь есть удобная формула расстояния от точки до прямой :

6) Вычислим площадь треугольника. Используем «школьную» формулу:

7) Уравнение медианы составим в два шага:

а) Найдём точку – середину стороны . Используем формулы координат середины отрезка.

Известны концы , и тогда середина:

б) Уравнение медианы составим по точкам :

– для проверки подставим координаты точек .

8) Найдём точку пересечения высоты и медианы:
в

Первое уравнение умножили на 5, складываем их почленно:
– подставим в первое уравнение:

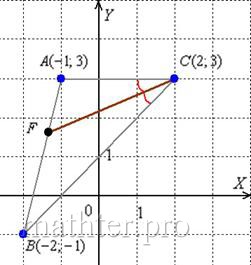
9) Биссектриса делит угол пополам:

Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:

Длины сторон уже найдены в предыдущих пунктах: .

Таким образом, . Координаты точки найдём по формулам деления отрезка в данном отношении. Да,

параметр «лямбда» получился просто сказочным, ну а кому сейчас легко? Точки известны и понеслась нелёгкая:

Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение – чтобы использовать формулу и

избавиться от иррациональности в знаменателе.

Разбираемся со второй координатой:

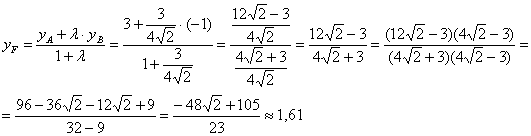
аким образом:

И предчувствие вас не обмануло, уравнение биссектрисы составим по точкам по формуле :

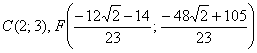
обратите внимание на технику упрощений:

Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)

10) Найдём центр тяжести треугольника.

Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца

в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то

теоретически фигура не должна свалиться.

Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.

Из пункта 7 нам уже известна одна из медиан: . Как решить задачу?

Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь

короче! Нужно только знать полезное свойство:

Точка пересечения медиан делит каждую из медиан в

отношении , считая от вершины треугольника. Поэтому справедливо

отношение
Нам известны концы отрезка – точки и .
По формулам деления отрезка в данном отношении:

Таким образом, центр тяжести треугольника:
И заключительный пункт задачи, для освоения которого нужно уметь решать недавно разобранные линейные

неравенства:

11) Составим систему линейных неравенств, определяющих треугольник.

Для удобства я перепишу найденные уравнения сторон:

Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится

вершина . Составим вспомогательный многочлен и вычислим его значение в точке : . Поскольку сторона принадлежит треугольнику, то неравенство будет нестрогим:

Внимание! Если вам не понятен этот алгоритм, то обратитесь к

Задаче 90.

Рассмотрим прямую . Треугольник расположен ниже данной прямой, поэтому

очевидно неравенство .

И, наконец, для составим многочлен , в который подставим координаты точки : .
Таким образом, получаем третье неравенство: .

Итак, треугольник определяется следующей системой линейных

неравенств:

Готово.

Какой можно сделать вывод?

Многие задачи аналитической геометрии прозрачны и просты,
главное, не допустить вычислительных ошибок.

Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них!

Главное, придерживаться методики решения и проявить маломальское упорство.

Ну что, может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =)

Но сейчас на очереди другая увлекательная тема, продолжаем изучать геометрию плоскости:

3.1. Алгебраическая линия и её порядок

2.8. Как научиться решать задачи по геометрии?

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Тема
2.2. Прямая на плоскости

Д
ве
взаимно перпендикулярные прямые, на
каждой из которых указано
положительное направление и масштаб,
образуют прямоугольную декартову
систему координат (рис: 2.6). :

Рис. 2.6

Точка

называется началом координат, ось

–
осью абсцисс, ось

-осью ординат. Положение на плоскости
любой точки

определяется двумя числами (координатами):

(рис.2.6).

Теорема 2.9 Расстояние

между точками

и

(рис.2.7) измеряется по
формуле

Рис. 2.7

Теорема 2.10 Если
точка

делит отрезок

в отношении

(
называется коэффициентом
пропорциональности), то ее координаты
находят так;

Следствие В частном случае, когда
отрезок делится пополам,
,
получим так называемые формулы половинного
деления;

Теорема 2.11 Площадь
треугольника

с известными вершинами

равна;

В декартовом базисе прямая изображается
уравнением первой степени с двумя
неизвестными

и

Рассмотрим различные формы задания
уравнения прямой на плоскости.

Теорема 2.12 В прямоугольной системе
координат

любая прямая задается уравнением первой
степени, называемым общим уравнением
прямой

где

– постоянные коэффициенты, причем
.

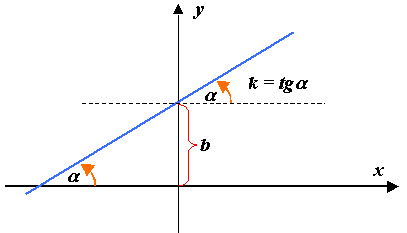
Уравнение прямой с угловым коэффициентом:

З
десь
параметры

и

имеют определенный геометрический
смысл (рис2.8).

Рис. 2.8

и называется угловым коэффициентом.

– угол, образованный прямой
с положительным направлением
.
В качестве положительного направления
измерения угла а принято направление
против хода часовой стрелки (рис.
2.8).

– отрезок, отсекаемый прямой на оси
ординат.

Выполнив несложные алгебраические
преобразования, можно от общего уравнения
прямой перейти к уравнению прямой с
угловым коэффициентом. При этом

Уравнение прямой в отрезках
выглядит так:

Здесь

и
–
отрезки, отсекаемые прямой на осях
абсцисс и ординат соответственно. Их
связь с коэффициентами общего уравнения

В этой форме можно представить уравнение
прямой, не проходящей через начало
координат, т.е. если
.

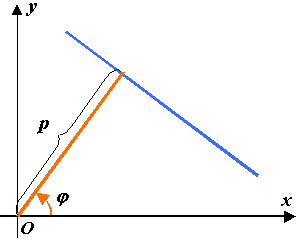
Нормальное уравнение прямой:

Геометрический смысл коэффициентов
этого уравнения:

– длина перпендикуляра,
опущенного из начала координат на
прямую;

– угол, образованный этим перпендикуляром,
с положительным направлением оси
(рис.2.9).

Рис. 2.9

Чтобы перейти к этому виду уравнения
прямой, надо умножить все члены общего
уравнения на нормирующий множитель

Знак

выбирается таким образом, чтобы

Уравнение пучка прямых описывает
множество прямых, проходящих через
точку

с известными координатами:

Уравнение прямой, проходящей через
две точки

и
:

Угол между прямыми

в зависимости от формы задания уравнений
прямых может быть найден по формуле:

или

З
десь
угол

измеряется от прямой с угловым
коэффициентом

или

до прямой с параметрами

или

(рис.2.10):

Рис. 2.10

Из этих формул легко выводятся условия
параллельности:

или

и перпендикулярности прямых:

или
.

Координаты точки пересечения
двух прямых определяются как
решение системы, составленной из
уравнений прямых.

Теорема 2.13
Расстояние

от точки

до прямой

(или
)
определяется по формулам:

или

Задача 2.5 Дано общее уравнение прямой
.

Написать: а) уравнение с угловым
коэффициентом; б) уравнение в отрезках;
в) нормальное уравнение. Построить
прямую.

Решение

а) Оставим член с

слева, а остальные перенесем в правую
часть уравнения. Затем разделим обе
части на коэффициент при
,
т.е. на -3. В результате
получим уравнение с угловым коэффициентом

Задача 2.6 Написать
уравнение прямой, проходящей через
точку

и отсекающей от координатного угла
треугольник, площадью равной
3.

Решение

О
чевидно,
что таких прямых будет 2,
а треугольники образованы во
втором и четвертом квадрантах (рис.2.11):

Рис. 2.11

Запишем уравнение пучка прямых, проходящих
через точку
:

Преобразуем его к уравнению в отрезках:

Таким образом,

Так как

и

имеют разные знаки, то площадь указанных
в условии задачи треугольников может
быть найдена по формуле

Отсюда

или

Решив квадратное уравнение, найдем

Тогда уравнения прямых будут иметь вид:

Задача 2.7 Дан
треугольник с вершинами

и
.
Написать уравнения сторон треугольника,
медианы
,
высоты
,
найти длины медианы

и высоты
,
угол при вершине
,
площадь треугольника
.

Решение

П
остроим
треугольник с указанными вершинами и
отметим все перечисленные элементы
(рис. 2.12).

Рис. 2.12

Уравнения, сторон треугольника получим,
используя уравнения прямой, проходящей
через две точки.

Уравнение

можно было записать и без таких выкладок,
учитывая, что обе точки лежат на оси
.

Для нахождения уравнения медианы

предварительно определим координаты
точки

как середины отрезка
:

Тогда уравнение медианы

будет иметь вид

Длину

определим как расстояние между точками

и
:

Запишем уравнение пучка прямых, проходящих
через вершину
:

Так как высота

перпендикулярна стороне треугольника
,
то их угловые коэффициенты связаны так:

Из уравнения

легко найти

Тогда
,
и уравнение высоты

будет

или

Длину высоты

определим как расстояние от точки

до прямой
:

Так как мы установили общие уравнения
прямых

и
,
то воспользуемся соответствующей
формулой для определения угла при
вершине

треугольника
.

Площадь треугольника

равна

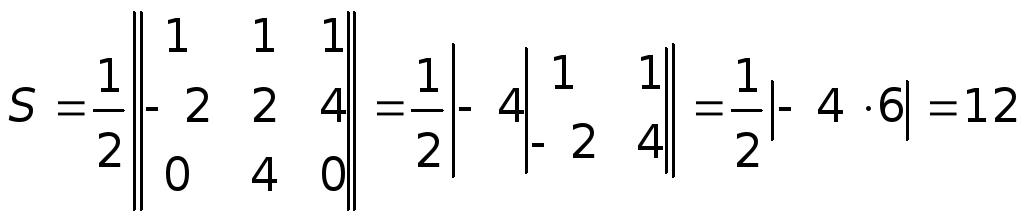
Задача 2.8 Найти
точку пересечения медиан и точку
пересечения высот треугольника, вершины
которого

и
.

Решение

С
троим
треугольник, показываем точки пересечения
его медиан и высот (рис.2.13).

Рис.2.13

Определим координаты точки

как середины отрезка
,
воспользовавшись формулами половинного
деления

Для определения координат точки
пересечения медиан

воспользуемся свойством этой точки,
согласно которому она делит медиану

в отношении
,
считая от вершины, т.е.
.
Тогда для точки