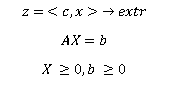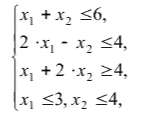Угловые точки области как найти

Найти угловые точки графика функции

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

1. Неравенства с отрицательными умножаем на (-1).
2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
4. Делаем замену переменных:

• Если , то
• Если — любой, то , где

Замечание: Будем нумеровать по номеру неравенства, в которое мы его добавили.

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m

Задача 34855 Построить множество решений системы.

Условие

Построить множество решений системы линейных алгебраических неравенств и
найти координаты угловых точек.

Решение

Граница каждой области -прямая, которая разбивает плоскость x_(1)Ox_(2) на 2 части

Строим прямую x_(1)+x_(2)=6
по двум точкам (0;6) и (6;0)

Выбираем произвольную точку из любой области, например, точку (0;0)
Подставляем в первое неравенство
0+0 ≤ 6 – верно.
Значит первое неравенство задает ту область, которая содержит точку (0;0)

Первое неравенство задает область 1 ( см. рис)

второе – область 2, .

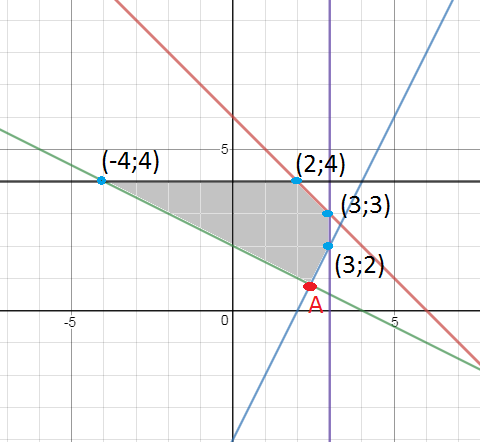
Система неравенств задает область на рис. 6

Координаты угловых точек-координаты границ, задающих неравенство.

Например, координаты точки А находим из системы:
<2x_(1)-x_(2)=4

Остальные координаты на рисунке ≤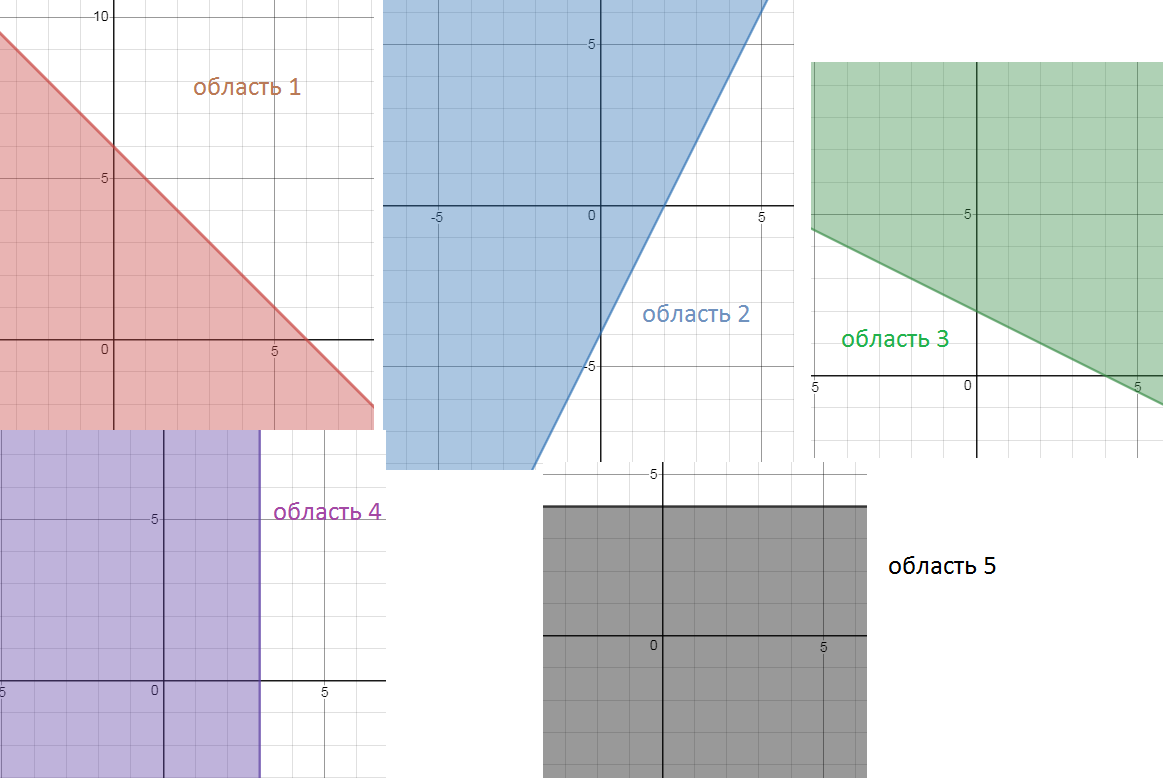

Решение систем уравнений

Содержание:

Графический метод решения систем уравнений

Вспоминаем то, что знаем

Что такое график уравнения с двумя неизвестными?

Что представляет собой график линейного уравнения с двумя неизвестными?

Решите графическим методом систему линейных уравнений:

Открываем новые знания

Решите графическим методом систему уравнений:

Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту

В курсе алгебры 7-го класса вы изучали системы линейных уравнений.

Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Начнём с графического метода

Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.

Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.

Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.

Возможно вам будут полезны данные страницы:

Примеры с решением

Пример 1:

Решим систему уравнений:

Построим графики уравнений

Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).

Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).

Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.

Ответ: (2; 5) и (-1; 2).

Пример 2:

Выясним количество решений системы уравнений:

Построим графики уравнений

Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.

Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.

Ответ: Два решения.

Решение систем уравнений методом подстановки

Вспоминаем то, что знаем

Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.

Решите систему линейных уравнений методом подстановки:

Открываем новые знания

Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?

Решите систему уравнений методом подстановки:

Как решить систему двух уравнений с двумя неизвестными методом подстановки?

Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?

Ранее вы решали системы уравнений первой степени.

Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.

Пример 3:

Пусть (х; у) — решение системы.

Выразим х из уравнения

Подставим найденное выражение в первое уравнение:

Решим полученное уравнение:

Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.

Чуть сложнее дело обстоит в следующем примере.

Пример 4:

Решим систему уравнений:

Пусть (х; у) — решение системы.

Выразим у из линейного уравнения:

Подставим найденное выражение в первое уравнение системы:

После преобразований получим:

Ответ: (-0,5; 0,5), (4; 5).

Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».

Пример 5:

Подставим во второе уравнение тогда его можно переписать в виде:

Теперь выразим х через у из первого уравнения системы:

Подставим в полученное ранее уравнение ху = 2:

Корни этого уравнения:

.

Иногда решить систему можно, используя метод алгебраического сложения.

Пример 6:

Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:

.

Корни этого уравнения:

Подставим найденные значения в первое уравнение. Рассмотрим два случая:

1)

2) , получим уравнение корней нет.

Иногда упростить решение удаётся, используя различные варианты замены неизвестных.

Пример 7:

Решим систему уравнений:

Обозначим

Второе уравнение системы примет вид:

Решим полученное уравнение. Получим, умножая обе части на 2а:

Осталось решить методом подстановки линейные системы:

Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями

Напомним, что при решении задач обычно действуют следующим образом:

1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;

2) решают полученную систему;

3) отвечают на вопрос задачи.

Пример 8:

Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.

Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — см.

Воспользуемся теоремой Пифагора:

Решим систему. Выразим из первого уравнения у:

Подставим во второе уравнение:

Корни уравнения:

Найдём

С учётом условия получим ответ: длина — 12 см, ширина — 5 см.

Пример 9:

Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.

Пусть х — первое число, у — второе число.

Тогда: — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.

Вычтем из второго уравнения первое. Получим:

Дальше будем решать методом подстановки:

Подставим в первое уравнение выражение для у:

Корни уравнения: (не подходит по смыслу задачи).

Найдём у из уравнения:

Получим ответ: 16 и 7.

Симметричные системы уравнений с двумя неизвестными

Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть не меняется. А вот уравнение не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть меняется.

Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.

ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.

Например, если в системе уравнений

переставить местами неизвестные х и у, то получим систему:

Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.

Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:

Сначала научитесь выражать через неизвестные выражения:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

[spoiler title=”источники:”]

http://reshimvse.com/zadacha.php?id=34855

http://natalibrilenova.ru/reshenie-sistem-uravnenij/

[/spoiler]

Как найти угловые точки

Поиск угловых точек или, как принято называть данное действие в общей терминологии – детектор точечных особенностей, является основным подходом, применяемым для извлечения особенностей изображения во многих системах компьютерных графических программ при переводе изображения в растровый вид.

Инструкция

На сегодняшний день существует несколько популярных способов поиска угловых точек, первым из которых является так называемый детектор Харриса, который представляет собой усовершенствованный Харрисом и Стивенсом алгоритм определения углов Моравека. Он состоит из нескольких основных этапов, которые позволяют с минимальной степенью погрешности и затрат времени произвести наиболее точную оценку угла. Здесь будут рассмотрены каждый из этапов работы по предложенному учеными алгоритму.

Суть изменения, которое внесли Харрис и Стивенс в привычный алгоритм Моравека, состоит в том, что оценка угла рассматривается непосредственно по направлению вектора угла, вместо использования сдвинутых пятен. С математической точки зрения данный метод использует способ суммы квадратов разностей. Для сохранения общности имеющейся структуры необходимо использовать условное отображение полутоновыми 2-хмерными изображениями, где само изображение задано переменной I. Выделенная область изображения на участке (U, V), рассматриваемая относительно его перехода по (x,y), где для обозначения суммы разностей этих областей применяется переменная S, определяемая по формуле:

В данной ситуации I(u+x, v+y) преобразуется при помощи рядов Тейлора. В результате чего, Ix и Iy примут вид производных от I:

Данные математические операции приведут вашу первоначальную формулу к следующему виду:

Таковое выражение можно переписать в матричном виде, где показатель «А» является структурой тензора:

Таким образом, данная формула принимает вид матрицы Харриса, в которой угловые скобки означает усреднение или суммирование (U,V). В сложившейся ситуации точечная особенность угла характеризуется значительным изменением показателя S во всех направлениях вектора, где на основании величины показателей значений производятся дополнительные вычисления:

По мнению Харриса и Стивенса, точное определение значений крайне трудозатратно, что требует введения дополнительной переменной М:

Данный тип преобразований позволяет без дополнительных затрат привести значения отрезка изображения в растровый вид при помощи поиска углов вектора.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Определение прямоугольных координат по топографической карте.

Прямоугольные
координаты определяют с помощью
координатной (километровой) сетки,
представляющей собой сеть линий,
параллельных экватору и осевому меридиану
зоны.

Для
определения прямоугольных координат
заданной точки (рис. 4) сначала нужно
найти координаты левого нижнего угла
квадрата, образованного линиями
километровой сетки, в котором расположена
точка. Т.е. X₀
и Y₀,
записанные в метрах.

Рис.
4. Определение прямоугольных координат.

Далее
необходимо из заданной точки опустить
перпендикуляры к левой и нижней линиям
километровой сетки, измерить с помощью
циркуля-измерителя длины отрезков и
перевести, используя численный масштаб,
в метры на местности. Получим приращения
прямоугольных координат ∆x
и ∆y.

Искомые
абсцисса и ординаты рассчитываются по
формулам:

X
= X₀
+ ∆x
Y
= Y₀
+ ∆y.

Полярные координаты.

Для
решения многих задач применяют полярные
координаты, когда положение заданной
точки относительной нулевой (полюса)
определяется углом
направления
между полярной осью и радиусом-вектором
и длиной
радиуса-вектора.
Единицы измерения, таким образом,
смешанные – градусы и метры.

В
качестве полярной оси может быть выбрано
любая линия: геодезический или магнитный
меридиан, произвольное направление, но
при работе с топографическими картами
чаще всего используются вертикальный
линии километровой сетки, т.е. линии,
параллельные оси Х. Угол, отсчитываемый
по часовой стрелке от северного
направления линии параллельной оси
абсцисс, проходящей через исходную
точку, до направления на искомую точку,
называется дирекционным
углом α.

Ориентирующие углы.

Кроме
дирекционного угла определить положения
заданного двумя точками направления
можно с помощью геодезического и
магнитного азимутов.

Геодезический
азимут
А_г
– угол, отсчитываемый по часовой стрелке
от северного направления геодезического
меридиана, проходящего через исходную
точку, до направления на объект.

Магнитный
азимут
А_m
– угол, отсчитываемый по часовой стрелке
от северного направления магнитного
меридиана, проходящего через исходную
точку, до направления на объект.

Угол
между меридианом точки и вертикальными
линиями прямоугольной координатной
сетки называется Гауссовым
сближением меридианов
γ.
Значение можно вычислить по формуле: γ
= (L
– L₀)
* sin
B.
Нетрудно заметить, что сближение
меридианов отсутствует на начальных
линиях отсчета: осевом меридиане и
экваторе. Значение Гауссова сближения
меридианов могут быть как положительными,
так и отрицательными, в зависимости от
положения от осевого меридиана. Хотя в
каждой точке может определено уникальное
значение Гауссова сближения меридианов,
их разброс по одному листу карты
незначителен. Поэтому для каждого листа
высчитывают среднее значение сближения
меридианов и указывают его в зарамочном
оформлении.

Угол
между северными направлениями
геодезического и магнитного меридианов
называется магнитным
склонением или
склонением магнитной стрелки D.
Магнитное склонение может быть восточным
(положительным) и западным (отрицательным),
что показывает, с какой стороны от
геодезического проходит магнитный
меридиан.

Величина
магнитного склонения на фиксированную
дату указана в зарамочном оформлении
топографической карты, там же обязательно
присутствует величина ежегодного
изменения магнитного склонения. Для
того, чтобы рассчитать действующее
значение магнитного склонения, необходимо
рассчитать поправку с учетом срока,
прошедшего от фиксированной даты и
прибавить ее к первоначальному значению.

Соотношение
дирекционного угла, геодезического и
магнитного азимутов определяют формулы:
А_г
= α + γ
и А_г
= А_m
+ D.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пример 1. Найти область решений (ОР) и область допустимых решений (ОДР) системы неравенств и определить координаты угловых точек ОДР

                

РЕШЕНИЕ. Найдем ОР первого неравенства: X₂ + 3X₂ ≥ 3.

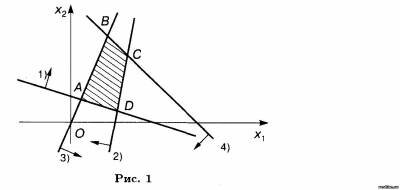
Построим граничную прямую X₁ +3X₂ – 3 = 0 (рис. 1).

Подставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решением неравенства (1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств системы.

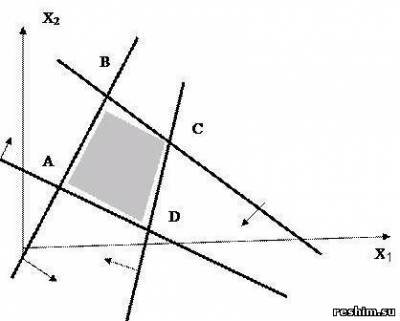
Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.
 

Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7). Точку В найдем как точку пересечения прямых

 

Из системы получим B(5/3, 10/3). Аналогично найдем координаты точек С и D: С(11/4; 9/14), D(3/10; 21/10).

Ответ: ОР и ОДР совпадают, является многоугольник ABCD.

Пример 2 Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР.

Решение.

Ответ: А(3/7, 6/7), В(5/3, 10/3), С(11/4, 9/4), D(21/10, 3/10), ОР и ОДР совпадают.

На следующем примере покажем отличие ОР и ОДР

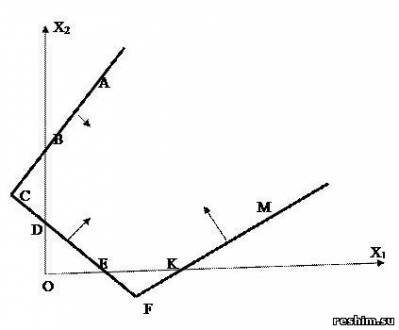
Пример 3. Найти ОР и ОДР системы неравенств

Решение.

Область решения (ОР) системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j = 1,n), называется областью неотрицательных, или допустимых, решений (ОДР).

Ответ: ACFM – ОР, ABDEKM – ОДР.

Общее решение и область допустимых значений системы неравенств могут иметь одну общую точку, рассмотрим данный случай на следующем примере.

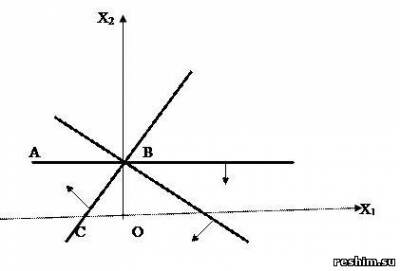
Пример 4.Найти ОР и ОДР системы неравенств

Решение.

Ответ:ABC – ОР, точка B – ОДР.

ОР и ОДР системы несовместные, смотри следующий пример.

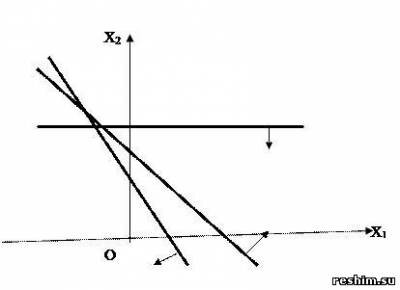
Пример 5.Найти ОР и ОДР системы неравенств

Решение.

Ответ: ОР и ОДР несовместны.

Для того, чтобы найти угловые точки: