Во многих областях науки и техники столь важным является понимание того, как определить угол альфа, потому что через него можно проанализировать и предсказать поведение различных механизмов, систем и процессов.
Определение угла альфа основано на измерении смещения между двумя линиями, плоскостями или направлениями. К примеру, в аэродинамике он находится между поверхностью летательного аппарата и вектором скорости, и сильно влияет на характеристики полета, в частности на подъемную силу и сопротивление.
Чтобы правильно определить угол альфа, необходимо точно знать, которые основные параметры важно учесть при расчете. В данной статье мы опишем подходы к определению угла альфа и приведем какие-то полезные рекомендации для изучения данной величины.
Кроме того, во время анализа важно понимать, как изменения характеристики воздействуют на поведение системы. К примеру, изменение угла атаки винта в приводе скорости воздушного судна может значительно повлиять на ход самолёта.
В результате, определение угла альфа представляет собой важный шаг в понимании работы различных механизмов и систем. Работа с рассчетом данного параметра может поспособствовать экономии ресурсов, оптимизации производительности или обеспечении безопасности.
Понятие угла альфа в математике
Определение угла альфа
Угол, обозначаемый как α, – это геометрическая величина, которая задает направление на плоскости. Можно представить угол как открывающийся, постепенно убывающий угол между двумя линиями на плоскости или между направлением вектора и осей декартовой системы координат. Обычно измеряется в радианах или градусах.
Физическое представление угла альфа
Наглядно, угол альфа можно представить начальным участком касательной к окружности окружностью, проведенной в данной точке. Вектор, ориентированный от начала координат в плоскости к данной точке, образует угол α с положительным направлением оси абсцисс. Иногда дополнительно выбирают значение λ (называемое арктангенсом), член единицы вектора, чтобы полностью определить точку по этим двум параметра.
Особенности:
- Угол альфа – безразмерная величина.
- В Интернете записываются порядковые соотношения.
- Обычно измеряется в радианах (π) и градусах.
Угол альфа – это фундаментальный математический термин, имеющий употребление, прежде всего, в социологии, статистике и физике. Его находят приоритетно важным, когда речь идет о силе и направлении в сети, проецируемых векторам и количественном анализе.
Определение угла альфа
Измеряется угол в градусах, радианах или оборотах. Каждый из этих видов измерения отличается по способу определения величины угла. Относясь к разным системам, углы имеют свои синонимы: градус, радиан и оборот.
Для определения угла в градусах, физики используют единицу измерения, которая называется градус. Одна зеркальная дуга равна 360 градусов. Определение угла альфа в градусах подразумевает косинусную функцию для преобразования побегов и углов в гармоничные соотношения.
Второй популярный способ определения угла альфа использует радианы. Минута дуги равна радиану. В данном измерении угол измеряется как годовое угловое расстояние от точки прямоугольной системы координат до точки сферы, ось которой совпадает с радианным меридианом. Интерпретируется как непрерывная физическая функция расстояния, которое должно быть преодолено одной единицей угла радиан.
Наконец, еще один способ определения угла альфа использует определённое количество оборотов. Один оборот равен одной части пи или μ Рот (микророту). Угловой момент оборота альфа характеризует соотношение сторон сторон фигуры и их друг к другу, а односторонние изменения в углу альфа оказанием силы по очагу обеспечивают реверсивный переход между многими операторными корреляциями, свойственными гравитационным полям.
Другими словами, определение угла альфа – это способ измерения дуги, разрывов, а также состава результатов разных сложных математических и физических задач, что делает его крайне полезным в задачах для кватернионами и операции с угловыми приращениями.
Применение угла альфа в разных дисциплинах
Угол альфа, как фундаментальная концепция, находит свое применение во многих дисциплинах, таких как геометрия, физика, статистика и иных областях науки и техники. В данном разделе мы рассмотрим основные примеры использования угла альфа во всемирной науке.
Применение угла альфа в геометрии
В геометрии угол альфа обозначает каждый определённый угол, и его можно определить путем измерения между двумя линиями или поверхностями. Угол измеряется в градусах от 0 до 180° или в радианах от 0 до π. В геометрии угол альфа используется для понимания соотношений между тремя или более линиями, например, при нахождении области треугольника.
Применение угла альфа в физике
В физике угол альфа имеет много применений, начиная от понимания релятивистского движения до измерения оптических свойств материалов. В механике тел вращения используют угол альфа для вычисления моментов силы и моментов импульса.
В оптике угол альфа может быть измерен в качестве угла Брюстера для определения угла отражения света от поверхности оптического материала, а также для анализа упругих свойств других материалов – например, определения предельного угла потери отражения.
В электродинамике угол альфа используется при исследовании полей электромагнитного излучения для понимания основных эффектов, связанных с электромагнитными волнами.
Применение угла альфа в статистике
В статистике угол альфа является важным параметром при тестировании гипотез. Угол альфа указывает на уровень значимости результата теста, и обычно составляет 0,05 или 0,01. Владельцы единиц оборудования с демонстрацией на рабочие местах будут узнаваемы при добровольном участия и активном участии. Если тест статистически значим, производительность рекомендуемого оборудования может быть выше или лучше, чем показатель арифметической функции, отображающий среднее.
Применение угла альфа в других областях науки и техники
Угол альфа также находит применение в различных других областях науки и техники, соответствующих этой дисциплине. В химии угол альфа используется для определения пространственного строения молекулы или мерила характеристики малых частей компонентов химических соединений. В медицине угол альфа может использоваться для изучения анатомии, особенно моделей Строя мышцы.
В данных научных областях угол альфа и другие геометрические понятия используются для понимания структуров и поведения систем. Это помогает ученым обеспечить надёжность их исследований и устанавливать взаимодействия и закономерности в различных явлениях.
| Сферирование | Презентация угла альфа |
|---|---|
| Геометрия | Различное измерение углов, отношения между линиями и поверхностями. |
| Физика | Вычисления силы и момента импульса, понимание свойств электромагнитных волн. |
| Статистика | Определение уровня значимости результатов тестов. |
| Химия | Определение строения молекул или пространственной структуры. |
| Медицина | Изучение анатомии и пространственных характеристик. |
Методы расчета угла альфа
В геометрии имеется множество методов определения угла альфа, которые можно разделить на несколько групп в зависимости от поставленной задачи и доступных данных. В данном разделе рассмотрим основные методы вычисления угла альфа при различных условиях.
Методы, использующие данные о сторонах треугольника
- Синусное правило:
Для нахождения угла альфа можно воспользоваться синусным правилом, которое гласит:
a:sin(A) = b:sin(B) = c:sin(C)
где a, b, c – стороны треугольника, A, B, C – соответствующие углы. Для того чтобы найти требуемый угол альфа, достаточно использовать соотношение, в котором заданы две стороны и угол, отличный от α.
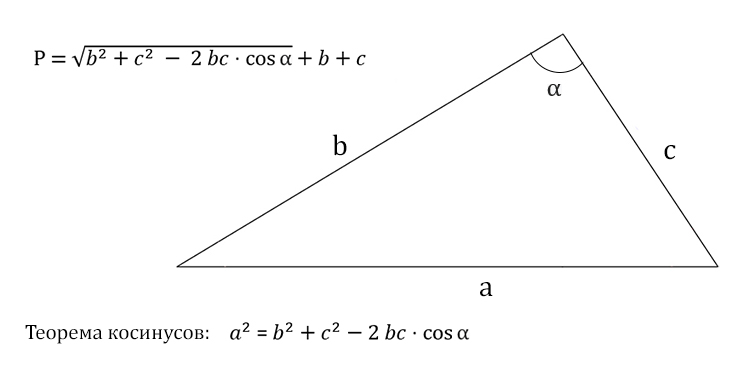
- Косинусное правило:
Косинусное правило позволяет определить угол альфа следующим образом: cos(α) = (b2 + c2 – a2) / (2bc).
Здесь же a, b, c – длины сторон треугольника, и для вычисления угла альфа используется соотношение с двумя известными сторонами и треугольником противоположного угла.
Методы, использующие данные о сторонах и двух углах треугольника
- Тангенсный метод:
Если известны длины двух сторон и угол между ними, то можно найти угол альфа через тангенс: tg(α) = sin(α) / cos(α).
Для этого нужно знать тангенсы углов треугольника, имеющих общим сторонами с углом α, а также использовать правила подстановки для поиска требуемого угла.
- Угло-сторонное правило:
Этот метод используется тогда, когда известен один угол и две стороны треугольника. В данном случае можно воспользоваться формулой: sin(α) = sin(A) *cos(B) / cos(A) * cos(B) + sin(A) * sin(B).
Здесь A – известный угол, B – угол, противолежащий стороне, испытывающей недостаток, а a и b – длины сторон, причастных к требуемому углу.
Влияние угла альфа на физические явления
1. Угол альфа в оптике
Угол альфа играет ключевую роль в оптике, определенном изучении излучения света. Один из основных примеров – это преломление света при переходе между двумя средами с разными показателями преломления. Угол альфа, под которым падает свет, сильно влияет на степень преломления, что, в свою очередь, влияет на направление и интенсивность излучаемого света.
2. Угол альфа в механике
Угол альфа также играет важную роль в механике, определяя характеристики движения тел в какой-либо среде.. К примеру, коэффициент сцепления, который описывает способность колеса автомобиля сопротивляться движению по дороге, трактуется с учетом угла наклона поверхности. Увеличение угла альфа приводит к уменьшению сцепления между колесом и дорогой, уменьшая крутящий момент на колёсе и ухудшая успешность преодоления препятствий.
Угол альфа также играет важную роль в аэродинамике, определяя характеристи
Практические задачи с использованием угла альфа
В данном разделе мы представим несколько практических задач, которые используют угол альфа. Мы рассмотрим различные области применения угла альфа и объясним, как его можно найти и использовать в каждом случае.
1. Геометрия
В геометрии угол альфа часто используется для определения отношений между сторонами прямоугольного треугольника. Здесь угол определяется как острый угол между двумя сторонами:
- y = \alpha – \beta, где y – угол между сторонами a и b.
- x = \alpha – \gamma, где x – угол между сторонами b и c.
Для решения геометрических задач с использованием угла альфа можно применять теорему Пифагора или теорему косинусов.
2. Радиосвязь
В радиосвязи угол альфа используется для определения направления распространения радиоволн. Угол альфа – это угол между направлением распространения радиосигнала и прямой в направлении передачи.
- Для измерения угла альфа можно использовать антенный направляющий круг в сочетании с интерферометрическим методом.
- Угол α может понадобиться для изменения настроек антенны и направления приемника, что в свою очередь приведет к улучшению качества радиосвязи.
3. Математический анализ
В языке математического анализа угол альфа может быть использован для анализа изменения приращений и обратно пропорциональных величин. Например, угол α можно использовать для вычисления как функции от частоты:
- F(α) = S * cos(α) * I, где S – параметр опорного вектора, I – изменение частоты
- S (α) = S * sin(α) * I
Для решения задач математического анализа с использованием угла α могут применять тестовые ИТ-граммы и решение пошагово заданных примеров.
Итак, разными областями применения угла альфа являются геометрия, радиосвязь, математический анализ и другие. В зависимости от цели и области применения, можно найти множество практических задач, где можно использовать угол α и применять различные методы для решения этих задач.
Вопрос-ответ:
Как определить, где нужно использовать угол альфа?
Угол альфа используется в разных областях науки и техники, где требуется определение угла поворота между векторами, плоскостями или линиями. Это может быть в трехмерной графике, механике, радиотехнике и других областях. В основном, угол альфа необходим для определения ориентации или направления движения некоторых объектов.
Что такое вектор, и каким образом он связан с углом альфа?
Вектор – это математический объект, представляющий направление и величину перемещения, статической силы или другого приложенного эффекта. Угол альфа используется для определения угла между двумя векторами, например, для определения направления силы, действующей на объект.
Существуют ли другие обозначения для угла альфа?
Да, угол альфа также может обозначаться другими буквами, такими как “θ” (тета) или “β” (бета), в зависимости от используемой системы обозначений или источника. В определенных областях, таких как антенны и радиотехника, угол альфа может иметь специальное название, связанное с применяемой сферой.
Есть ли какие-то упрощенные способы вычисления угла альфа для обычных людей, не имеющих сильных математических навыков?
Да, существуют некоторые упрощенные правила для нахождения угла альфа, например, используя геометрический интуитивный подход. Однако, для более точного вычисления, самая простота берется тригонометрия: угол альфа можно найти через тангенс, косинус или синус двух слагаемых векторов. Независимо от математической хватки, для обычных задач существуют также многочисленные онлайн-калькуляторы, которые могут выполнить эти вычисления автоматически.