В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.
В трехмерном пространстве имеются скрещивающиеся прямые a и b. Проведем прямые а1 и b1 параллельные скрещивающимся a и b. Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b1 являются пересекающимися прямыми.
Обозначим угол между a1 и b1 равным значению α. Построение прямых a2 и b2 параллельно скрещивающимися относительно a и b в точке М2 отличной от М1 приводит к тому, что значение угла между ними обозначим как α. То есть угол между прямыми a1 и b1 равен углу между a2 и b2. В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М1 и М2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.
Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат Охуz. Имеется задача, в которой необходимой найти угол α, образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M, что дает понять, через нее проходят прямые a1 и b1, которые параллельны скрещивающимся a и b. Угол α , образованными прямыми a и b, из этого определения получится равным пересекающимся a1 и b1.
Для нахождения искомого угла между a1 и b1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a1 и b1.
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a→=(ax, ay, az) и b→=(bx, by, bz).
Векторы a→ и b→ имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α=arccosa→, b→a→·b→=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2, а a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2.
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α=1-cos2 α.
Найти угол между скрещивающимися прямыми a и b, которые заданы уравнениями x2=y-40=z+1-3 и x=1+λy=1-λz=-3+4·λ, λ∈R и определяются в системе координат Охуz.
Решение
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a→=(2, 0, -3) является направляющим вектором прямой x2=y-40=z+1-3. При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b→=(1, -1, 4) является направляющим вектором для прямой вида x=1+λy=1-λz=-3+4·λ, λ∈R.
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2=arccos2·1+0·(-1)+(-3)·422+02+(-3)2·12+(-1)2+42==arccos1013·18=arccos10326
Ответ: угол между скрещивающимися прямыми равен arccos10326.
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра AD и ВС, принадлежащие пирамиде ABCD, с известными вершинами с координатами A(0, 0, -1), B(5, 7, -5), C(3, 7, -5), D(1, 3, 1).
Решение
AD→ и BC→ являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что AD→=(1-0, 3-0, 1-(-1))⇔AD→=(1, 3, 2)BC→=(3-5, 7-7, -5-(-3))⇔BC→=(-2, 0, -2)
Из формулы cos α=arccosAD→, BC→AD→·BC→ находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α=1·(-2)+3·0+2·(-2)12+32+22·(-2)2+02+(-2)2=614·8=327
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α=1-cos2α=1-3272=1927.
Ответ: sin α=1927, cos α=327.
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
Имеется прямоугольный параллелепипед ABCDA1B1C1D1 со сторонами АВ=3, АD=2 и AA1=7 единиц. Точка E делит прямую АА1 как 5:2. Определить угол между скрещивающимися прямыми ВЕ и А1С.
Решение
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат Охуz. Получаем, что начало координат является совпадающим с вершиной A, а Ох совпадает с прямой AD, Оу с AB, а Оz с АА1. Рассмотрим рисунок, приведенный ниже.
Отсюда имеем, что точка B с координатами (0, 3, 0), E – (0, 0, 5), AА – (0, 0, 7), C – (2, 3, 0). Исходя из координат, мы можем получить координаты векторов BE→ и A1C→, необходимые для дальнейшего решения задачи. Получаем, что BE→=(0, -3, 5), A1C→=(2, 3,-7).
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α=arccosBE→, A1C→BE→·A1C→=arccos0·2+(-3)·3+5·(-7)02+(-3)2+52·22+32+(-7)2==arccos4434·62=arccos22527
Ответ: arccos22527.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD). 
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
11
Авг 2013
Категория: Справочные материалы
Углы в пространстве
2013-08-11
2014-03-03
Угол между пересекающимися прямыми
Углом между пересекающимися прямыми, называется наименьший из углов, образованных при пересечении этих прямых (если при пересечении образовались четыре равных угла, то прямые перпендикулярны).
Угол между скрещивающимися прямыми
Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).
Угол между прямой и плоскостью
Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость
Угол между плоскостями
Угол между плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
Этот угол не зависит от выбора такой плоскости.
Угол между двумя параллельными плоскостями принимается равным нулю.
Автор: egeMax |
Нет комментариев
Скрещивающиеся прямые
Как определяется угол между скрещивающимися прямыми?
Ты можешь спросить, а чего тут определять? Угол, он и в Африке (то есть в пространстве) – угол!
И действительно, если прямые лежат в одной плоскости, то угол между ними ищется так же, как и на плоскости:
Наименьший из двух углов, образованных при пересечении.
Но что же делать, если прямые совсем не пересекаются?
Читай эту статью и всё узнаешь!
Скрещивающиеся прямые — коротко о главном
Если прямые лежат в разных плоскостях (т.е. не пересекаются), нужно через произвольную точку на одной прямой (например, прямая ????) провести прямую, параллельную другой прямой (например, прямую ????′, где ????′||????.
Скрещивающиеся прямые — подробнее
Как найти угол, если прямые не пересекаются?
Вот, например: прямые ( displaystyle a) и ( displaystyle b) скрещиваются. Какой угол между ними?
Чтобы это определить, делаем так: через произвольную точку одной прямой (например ( displaystyle b)), нужно провести прямую ( displaystyle {a}’||a).
И тогда угол между ( displaystyle a) и ( displaystyle b) будет равен (по определению!) углу между ( displaystyle {{a}’}) и ( displaystyle b).
Да, но как это применить в задачах? Давай посмотрим.
Решение задач на угол между скрещивающимися прямыми
В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) найти угол между ( displaystyle AC) и ( displaystyle D{{C}_{1}}).
Решаем:
Прямые ( displaystyle AC) и ( displaystyle D{{C}_{1}}) не пересекаются, но нужно как-то найти угол между ними.
Пользуемся правилом: через точку ( displaystyle {{C}_{1}}) проведем прямую ( displaystyle {{A}_{1}}{{C}_{1}}). Она будет параллельна ( displaystyle AC).
Значит, угол между ( displaystyle AC) и ( displaystyle D{{C}_{1}}) равен углу между ( displaystyle {{A}_{1}}{{C}_{1}}) и ( displaystyle D{{C}_{1}}). Осталось его найти.
Смотри: ( displaystyle {{A}_{1}}{{C}_{1}}), ( displaystyle {{A}_{1}}D) и ( displaystyle D{{C}_{1}}) – диагонали граней куба, поэтому ( displaystyle {{A}_{1}}{{C}_{1}}={{C}_{1}}D={{A}_{1}}D), то есть ( displaystyle Delta {{A}_{1}}{{C}_{1}}D) – равносторонний.
Поэтому ( displaystyle angle {{A}_{1}}{{C}_{1}}D=60{}^circ ).
Ответ: ( displaystyle 60{}^circ ).
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
Задачи на скрещивающиеся прямые и углы между ними попадаются сплошь и рядом в этом вебинаре.
ЕГЭ 8. Куб. Параллелепипед. Призма – расстояния и углы в пространстве
На этом уроке мы на примере самых простых объемных фигур научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми
Две пересекающиеся прямые образуют смежные и вертикальные углы. Вертикальные углы равны, а смежные углы дополняют друг друга до 180°.Угловая мера меньшего из них называется углом между прямыми. Угол между перпендикулярными прямыми равен 90° по определению. Угол между параллельными прямыми считаем равным нулю.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
Этот угол не зависит от того, какие взяты пересекающиеся прямые. Докажем это.
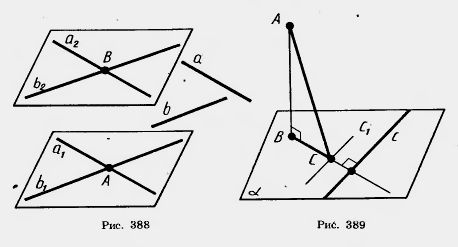
Пусть а1b1 — пересекающиеся в точке А прямые, параллельные данным скрещивающимся прямым а и b (рис. 388). Пусть а2b2 — другие прямые, параллельные данным и пересекающиеся в точке В. По теореме 16.2 прямые а1 и a2 параллельны (или совпадают) и прямые b1 и b2 параллельны (или совпадают).
Выполним параллельный перенос, при котором точка А переходит в точку В. Так как при параллельном переносе каждая прямая переходит либо в себя, либо в параллельную прямую, то указанный параллельный перенос переводит прямую а1 в прямую а2, а прямую b1 в прямую b2. Так как параллельный перенос сохраняет величину угла, то угол между прямыми а1 и b1 равен углу между прямыми a2 и b2. А это и требовалось доказать.
По данному ранее определению перпендикулярными называются прямые, пересекающиеся под прямым углом. Однако иногда скрещивающиеся прямые тоже называются перпендикулярными, если угол между ними равен 90°.
Задача (33). Докажите, что любая прямая на плоскости, перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Решение. Пусть АВ — перпендикуляр к плоскости 
, АС — наклонная и с — прямая в плоскости , перпендикулярная ВС (рис. 389). Проведем через основание С наклонной прямую c1llс.
По теореме о трех перпендикулярах c1 перпендикулярна наклонной АС. А так как угол между прямой с и наклонной АС равен углу между прямыми АС и c1, то прямая с тоже перпендикулярна наклонной АС.
Обратно: если прямая с перпендикулярна наклонной АС, то прямая с, тоже перпендикулярна ей, а значит, по теореме о трех перпендикулярах и ее проекции ВС. Так как с||c1, то с
ВС.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урокаконспект урока
конспект урока
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
