Уравнение окружности как найти игрек

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график – ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Уравнение окружности

Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид

1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).

Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).

По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.

Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.

2. Если пара чисел (x_o;y_o) удовлетворяет данному уравнению, то

А это значит, что расстояние между точками C(x_o;y_o) и A(a;b) равно R. Значит, точка C(x_o;y_o) принадлежит окружности с центром в точке A(a;b) и радиусом R.

Следовательно, данное уравнение фигуры является уравнением окружности.

[spoiler title=”источники:”]

http://www.calc.ru/Uravneniye-Okruzhnosti.html

Уравнение окружности

[/spoiler]

In geometry, a circle can be defined as the set of all points that are equidistant from a fixed point in the plane, where the fixed point is the center of the circle. The radius is defined as the distance between any point on the circumference of a circle and the center of the circle. The largest chord that passes through the center of the circle; this diameter is referred to as the circle’s diameter. 

Equation of a Circle

A circle can be defined as a closed curve traced out by a point that moves in a plane such that the distance from the given point in that plane is always constant. By using the equation of a circle, we can describe a circle in an algebraic way when the center of the circle and its radius length is known. We require an algebraic equation to represent the circle on a Cartesian plane. So, to find the position of the circle on a Cartesian plane, we require the coordinates of the center and the length of its radius.

The standard form of the equation of a circle

Let’s consider a circle with a center (h, k) and P (x, y) to be any point on the circumference of the circle for finding the standard form of the equation. From the definition of the radius of the circle, 

The radius of the given circle (r) = CP

We can find the value of CP By using the formula for the distance between two points i.e.,

CP = r = √[(x – h)² + (y – k)²]

Now, by squaring on both sides we get,

(x – h)² + (y – k)² = r²

Hence, the standard form of the equation of a circle is,

(x – h)² + (y – k)² = r²

Where (h, k) is the center of the circle and r is the length of the radius.

• Equation of the circle with the center at the origin

Let’s consider that the center of the circle lies at the origin (0, 0) and its radius is “r”. Now, the distance between the origin and any point P (x, y) on the circle is the radius of the circle, i.e.,

OP = r

By using the formula for the distance between two points, 

OP = r = √[(x – 0)² + (y – 0)²]

Now, by squaring on both sides, 

r² = x² + y²

Hence, the equation of the circle with the center at the origin is

x² + y² = r²

• Equation of the circle passing through the origin

Let’s consider that a circle with a center C (h, k) and a radius “r” is passing through the origin. The distance between the center of the circle and the origin is the radius of the circle, i.e.,

OC = r

Draw a line from the center to a point M (h, 0) on the X-axis such that CM is perpendicular to OM.

From the Pythagorean theorem;

OC² = OM² + CM²

r² = h² + k²

Hence, the equation for the circle passing through the origin is,

r² = h² + k²

• Equation of the circle with the center lying on the X-axis

Assume that the center of circle C (h, 0) is on the X-axis and its radius is “r.”

Now, the distance between the center of the circle and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points, we get

CP = r = √[(x – h)² + (y – 0)²]

Now, by squaring on both sides, we get

r² = (x – h)² +y²

Hence, the equation for the circle passing through the origin is,

(x – h)² +y² = r²

• Equation of the circle with the center lying on the Y-axis

Let’s consider that the center of circle C (0, k) lies on the Y-axis and its radius is “r”. Now, the distance between the center of the circle and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points, 

CP = r = √[(x – 0)² + (y – k)²]

Now, by squaring on both sides we get,

r² = x² +(y – k)²

Hence, the equation of the circle with the center lying on the Y-axis is,

x² +(y – k)² = r²

• Equation of the circle touching the X-axis

Let us consider that the center of circle C (h, r) is touching the X-axis and its radius is “r”. Now, the y-coordinate of the center of the circle touching the X-axis is equal to the radius “r”.

Now, the distance between the center of the circle C (h, r) and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r 

By using the formula for the distance between two points, we get

CP = r = √[(x – h)² + (y – r)²]

Now, by squaring on both sides we get,

r² = (x – h)² +(y – r)²

Hence, the equation of the circle touching the X-axis is

 (x – h)² +(y – r)² = r²

• Equation of the circle touching the Y-axis

Let’s consider that the center of circle C (r, k) is touching the Y-axis and its radius is “r”. Now, the x-coordinate of the center of the circle touching the Y-axis is equal to the radius “r”. Now, the distance between the center of the circle C (r, k) and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points,

CP = r = √[(x – r)² + (y – k)²]

Now, by squaring on both sides we get,

r² = (x – r)² +(y – k)²

Hence, the equation of the circle touching the Y-axis is

(x – r)² +(y – k)² = r²

• Equation of the circle touching both the X-axis and the Y-axis

Let’s assume that a circle with a center C (r, r) with a radius “r” is touching both the X-axis and the Y-axis. As the circle touches both the X-axis and the Y-axis, the x and y coordinates of the center become equal to the radius of the circle “r”.

Now, the distance between the center of the circle C (r, r) and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points, 

CP = r = √[(x – r)² + (y – r)²]

Now, by squaring on both sides we get

r² = (x – r)² +(y – r)²

Hence, the equation of the circle touching both the X-axis and Y-axis is

(x – r)² +(y – r)² = r²

General Equation of a Circle

The general equation of a circle is given as,

x²+ y² + 2gx + 2fy + c = 0

For all values of g, f, and c.

x² + y² + 2gx + 2fy + c = 0

By adding g² + f² on both sides we get,

x² + y² + 2gx + 2fy + c + g² + f² = g² + f²

Now, by arranging the equation we get

(x² + 2gx + g²) + (y² + 2fy + f²) = g² + f² – c

We know that, (x + g)² =(x² + 2gx + g²) and (y + f)² = (y² + 2fy + f²). So, by substituting these values in the above equation we get

(x + g)² + (y + f)² = g² + f² – c

By comparing the above equation with the standard form of the equation we get

h = -g, k = -f and r² = g² + f² – c 

Where (h, k) are the coordinates of the center of a circle and “r” is its radius.

Hence, the equation x²+ y² + 2gx + 2fy + c = 0 represents a circle having center (-g, -f) and radius r equal to r² = g² + f² – c

• The radius of a circle is real if g² + f² > c.
• The radius of a circle becomes imaginary if g² + f² < c. Hence, the circle will be having a real center and an imaginary radius.

Sample Problems

Problem 1: Find the equation of a circle with the center at the origin and having a radius of 6 units.

Solution:

Given data,

Center of the circle = (0,0) and the radius = 6 units

We know that,

The equation of a circle whose center is at the origin is,

x² + y² = a²

Where a is the radius of the circle.

So, the equation of the circle having a radius of 6 units is,

x² + y² = (6)²

x² + y² = 36

Hence, the equation of the given circle is x² + y² = 36

Problem 2: Find the radius and the center of a circle if the equation of the circle is x² + y² – 8x + 6y + 9 = 0

Solution:

Given data,

The equation of the circle is x² + y² – 8x + 6y + 9 = 0

We can see the  given equation is in the form of  x²+ y² + 2gx + 2fy + c = 0

Now by comparing the both equations,

2g = -8 ⇒ g = -4

2f = 6 ⇒ f = 3

c = 9

Center of the circle = (-g, -f) = (4, -3)

Radius of the circle (a) = √(g² + f² – c)

⇒ a = √[(-4)² + 3² – 9] = √(16 + 9 – 9)

a = √16 = 4 units

Hence, the center of the given circle is (4, -3) and its radius is 4 units.

Problem 3: Find the equation of the circle whose center is (5, 0), and radius is 7 units.

Solution:

Given data,

Center of a circle = (5, 0)

Radius of the circle = 7 units

The general equation of a circle with center (h, k) and radius “a” units is,

(x – h)² + (y – k)² = a²

Now, the equation of the given circle is,

(x – 5)² + (y – 0)² = (7)²

⇒ x² – 10x + 25 + y² = 49

⇒ x² + y² – 10x – 24 = 0

Therefore, the equation of the given circle is x² + y² – 10x – 24 = 0

Problem 4: Find the equation of the circle center passing through the Y-axis whose center is (0,-6) and radius is 10 units. 

Solution:

Given data,

Center of a circle = (0,-6)

The radius of the circle = 10 units.

We know that,

The equation of the circle with the center lying on the Y-axis is,

x² +(y – k)² = r²

x² + (y + 6)² = (10)²

x² + y² + 12y + 36 = 100

x² + y² + 12y – 64 = 0

Hence, the equation of the circle is x² + y² + 12y – 64 = 0

Problem 5: Find the equation of the circle with a radius of 6 inches that touches both the X-axis and the Y-axis.

Solution:

Given data,

The radius of the circle = 6 inches.

As the circle touches both the X-axis and the Y-axis, the x and y coordinates of the center become equal to the radius of the circle “r”.

Hence, the center of the circle = (6,6)

We have,

The equation of the circle touching both the X-axis and Y-axis is

(x – r)² +(y – r)² = r²

(x – 6)² + (y – 6)² = 6²

x² -12x + 36 + y² – 12y + 36 = 36

x² + y² -12x -12y + 36 = 0

Hence, the equation of the circle touching both the X-axis and Y-axis is x² + y² -12x -12y + 36 = 0

Problem 6: Find the equation of the circle with the center at (-7, 4) and the radius of 4 units and touch the X-axis.

Solution:

Given data,

Center of the circle = (-7, 4)

The radius of the circle = 4 units

The equation of the circle touching the X-axis is

(x – h)² +(y – r)² = r²

(x + 7)² + (y – 4)² = 4²

x² + 14x + 49 + y² – 8y + 16 = 16

x² + y² + 14x – 8y + 49 = 0

Hence, the  equation of the circle touching the X-axis is x² + y² + 14x – 8y + 49 = 0

Problem 7: Find the equation of the circle with a radius of 5 units and is touching the Y-axis at the point (0,-3).

Solution:

Given data,

The radius of the circle = 5 units.

The circle is touching the Y-axis at (0,-3)

Now, the x-coordinate of the center of the circle touching the Y-axis is equal to the radius “4 units”.

Hence, the coordinates of the center = (5, -7)

We have,

The equation of the circle touching the Y-axis is

(x – r)² + (y – k)² = r²

(x – 5)² + (y + 3)² = 5²

x² – 10x + 25 + y² + 6y + 9 = 25

x² + y² -10x + 6y + 25 = 0

Hence, the equation of the circle touching the Y-axis is x² + y² -10x + 6y + 25 = 0

Каждое уравнение с
двумя переменными  х  и  у  определяет некоторое множество пар  (х; у)  значений
переменных, которые являются решениями этого уравнения, т. е. задаёт некоторое
отношение между значениями переменной  х  и значениями
переменной  у. График отношения, заданного уравнением с двумя
переменными, или, короче, график уравнения с двумя переменными, есть, как
известно, множество точек плоскости, координаты которых служат решениями
уравнения. Мы знаем, что графиком уравнения вида  ax + by = c,
где  a ≠ 0  или  b ≠ 0,
служит прямая линия, график уравнения вида  

y = ax² +
bx + c (a ≠ 0)   

парабола, график
уравнения вида  

xy = k

гипербола.

На рисунку
изображён график уравнения 

х² + 9у²
= 81.

Кривая такого вида
называется эллипсом.

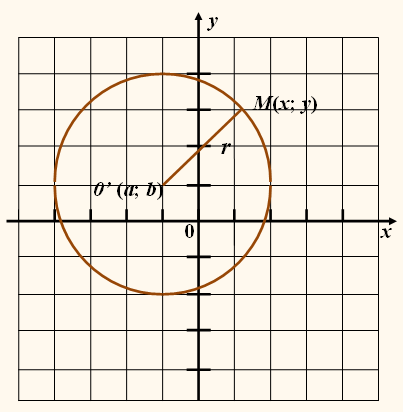
Графиком уравнения

(x – a)² +
(y – b)² =
r²

является окружность на координатной плоскости  хОу  с центром в точке  О’(a; b)  и радиусом 
r (r
> 0).

Уравнением фигуры
на плоскости  в декартовых координатах
называется уравнение с двумя переменными 
х  и  у, которые будут координатами любой точки фигуры. И наоборот:
любые два числа, которые будут решением этого уравнения, будут координатами некоторой
точки фигуры.

Составим уравнение окружности
с центром в точке  А₀(а; b)  и радиусом  R.

Возьмём произвольную
точку  А(х; у)  на окружности. Расстояние от неё до
центра  А₀  равно  R. Квадрат расстояния от точки  А  до  А₀  равен:

(х – a)²
+ (у – b)².

Таким образом, координаты  х, у  каждой точки  А  окружности будут корнями уравнения:

(х – a)²
+ (у – b)² = R².

Наоборот: любая
точка  А, координаты которой будут решениями уравнения, принадлежат окружности, так как расстояние
от неё до точки  А₀  равно  R. Отсюда вытекает, что это уравнение будет уравнением окружности
с центром  А₀  и радиусом 
R.

Обратите внимание, что
когда центром окружности будет начало координат, то уравнение окружности имеет
вид:

х² + у² = R².

ПРИМЕР:

Какая геометрическая фигура задано уравнением ?

х² + у²
+ ах + bу + с = 0.

РЕШЕНИЕ:

видим, что искомая фигура – окружность с центром

ПРИМЕР:

Построить график уравнения:

х² + у²
= 16.

Перепишем уравнение в виде

(х – 0)² + (у – 0)² = 4².

Графиком этого уравнения является окружность с центром в
точке  О(0;
0)  и
радиусом  4.

ПРИМЕР:

Построить график уравнения:

(х – 1)² + (у – 2)² = 9.

Перепишем уравнение в виде

(х – 1)² + (у – 2)² = 3².

Графиком этого уравнения является окружность с центром в
точке  (1;
2)  и
радиусом  3.

ПРИМЕР:

Построить график уравнения:

х² + у²
+ 4х = 0.

Перепишем уравнение в виде

х² +
4х + 4 + у² = 4,

(х + 2)² + у²
= 4,

(х – (–2))² + (у – 0)² = 2²,

Графиком этого уравнения является окружность с центром в
точке  (–2;
0)  и
радиусом  2.

От графиков функций
необходимо отличать графики уравнений.

ПРИМЕР:

На координатной плоскости изображена окружность радиусом  r = 5  с центром в начале координат. Уравнение этой окружности:

х² + у²
= 25.

Можно сказать и так: графиком уравнения 

х² + у²
= 25 

будет окружность, изображённая на рисунку.

А можно график уравнения 

х² + у²
= 25 

считать графиком некоторой функции ? Нет. Если переменные  х  и  у  связаны соотношением 

х² + у²
= 25,

то одному значению 
х = 3  соответствует два
разных значения переменной  у:  4  и  –4.
А соотношение между переменными  х  и  у  только тогда считается функцией, когда каждому
значению  х  из области определения соответствует одно
значение  у.
График уравнения только тогда будет графиком некоторой функции, если каждая
прямая, параллельная оси  у, пересекает
его не больше чем в одной точке.

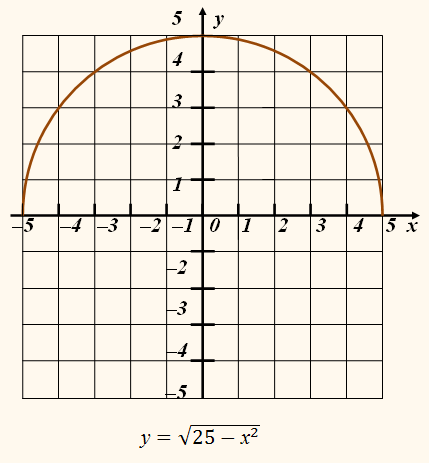
ПРИМЕР:

Изображённые на рисунке полуокружности – графики функций

Их объединение – вся окружность – график не функции, а уравнения  

у² = 25 – х², или 

у² +
х² = 25.

Задания к уроку 27

Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.

Сегодня на уроке мы
попробуем по геометрическим свойствам линии найти ее уравнение.

В качестве линии
рассмотрим окружность радиуса  с
центром в точке .

Пусть центр
окружности имеет координаты . Возьмем на
окружности произвольную точку . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC² = r².
Заменим MC² квадрат на выражение  и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами  имеет вид: .

Задача. Записать
уравнение окружности с радиусом  и центром в начале
координат.

Решение.

Начало координат
имеет координаты (0;0). Подставим их в уравнение окружности и получим, что
уравнение окружности с радиусом r и
центром в начале координат имеет вид

 

.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего,
определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь
давайте определим величину радиуса окружности.

Поскольку в правой
части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо
извлечь квадратный корень из 4. Получим 2.

 Значит наша
формула задает окружность с центром в точке с координатами пять три и радиусом
равным двум.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего
определимся с координатами центра окружности.

Это будут числа -4
и 2. Теперь давайте определим величину радиуса окружности.

Задача. Начертить
окружность, заданную уравнением .

Решение. Уравнениями
такого типа описываются окружности с центром в начале координат. Теперь давайте
определим величину радиуса окружности. Поскольку в правой части формулы стоит
квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень
из 9.

Значит наша формула
задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.

Теперь давайте
попробуем решить задачу обратную данным.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).

Нетрудно заметить,
что радиус окружности равен 4.

Запишем уравнение
окружности и подставим найденные значения.

 

 

 

Ответ: .

Решим еще одну
задачу.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

 – центр окружности

 – радиус окружности

Ответ:.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

 – центр окружности

 – радиус окружности

 

 

 

Ответ:.

Решая задачи, мы с
вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот
порядок.

Для того, что
бы составить уравнение окружности и построить ее надо:

1. Найти координаты
центра окружности.

2. Найти длину
радиуса этой окружности.

3. Записать уравнение
окружности.

4. Подставить
полученные значения в уравнение окружности.

5. Построить
окружность, если это требуется для решения задачи.

Рассмотрим еще одну
задачу.

Написать уравнение
окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм
имеет координаты шесть три.

Задача. Написать
уравнение окружности с диаметром , если , .

Решение.

Найдем координаты
центра окружности. Центр окружности является серединой диаметра. Воспользуемся
формулами для нахождения координат середины отрезка.

Получим, что центр
окружности имеет координаты .

Теперь определим
радиус окружности. Для этого найдем расстояние от центра окружности до концов
диаметра.

 

 

Запишем общее
уравнение окружности и подставим в него найденные значения. Тогда получим, что
уравнение данной окружности имеет вид:

Ответ: .

Подведем итоги
урока.

На сегодняшнем
уроке мы познакомились с формулой, которая задает окружность с центром в точке С
(x₀; y₀)
и радиусом r.

Также мы
познакомились с формулой, которая задает окружность с центром в начале
координат и радиусом r.

Мы рассмотрели
задачи на составление уравнения окружности по рисунку и на построение
окружности по заданному уравнению.