Урок как найти общий знаменатель дроби

Математика

5 класс

Урок № 51

Приведение дробей к общему знаменателю

Перечень рассматриваемых вопросов:

• основное свойство дроби;
• общий знаменатель дробей;
• дополнительный множитель;
• НОК двух чисел;
• наименьший общий знаменатель.

Тезаурус

Общий знаменатель – это число всегда положительное, на которое делятся знаменатели данных дробей.

Наименьший общий знаменатель – это наименьшее положительное число, кратное знаменателям данных дробей.

Дополнительный множитель – это число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель.

Обязательная литература:

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Вы уже знаете, что дробь в математике – это число, состоящее из одной или нескольких частей единиц, и умеете определять и называть часть целого.

Вопрос: какая часть яблока на картинке?

Ответ:

Вопрос: какая часть пиццы осталась на тарелке?

Ответ: .

Или, например, круг разделили на восемь частей. Четыре части закрасили в другой цвет: значит, закрашено части круга.

Но, если посмотреть внимательнее, четыре доли круга, разделённого на восемь частей, – это ровно половина. Значит, дробь равна дроби .

Вспомним основное свойство дроби.

Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.

Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю.

Для этого найдём число, которое делится на 8 и 3, – например, число 24.

Дополнительный множитель обычно пишут слева над числителем:

Приведём дроби к знаменателю 24. Для этого умножим числитель и знаменатель дроби на дополнительный множитель 3.

Теперь умножим числитель и знаменатель дроби на дополнительный множитель 8.

Дробииприведены к общему знаменателю.

Далее приведём дроби и к наименьшему общему знаменателю.

Так как наименьшее общее кратное (НОК) чисел 36 и 54 равно 108, то наименьший общий знаменатель этих дробей также равен 108.

Соответственно, чтобы привести дробь к знаменателю 108, необходимо и числитель, и знаменатель дроби умножить на 3:

Чтобы привести дробь к тому же знаменателю, умножаем и числитель, и знаменатель этой дроби на 2:

Таким образом, алгоритм приведения дробей к наименьшему

1. деление на простые множители знаменателей дробей;
2. поиск наименьшего общего кратного(НОК)для знаменателей этих дробей;
3. приведение дроби к общему знаменателю, то есть умножение и числителя, и знаменателя дроби на множитель.

Итак, сегодня мы научились находить наименьший общий знаменатель дробей двумя способами:

• первый способ – перемножить знаменатели этих дробей;
• второй способ – найти наименьшее общее кратное этих дробей.

Тренировочные задания

№ 1. Для дроби выберите из представленных равную ей дробь со знаменателем 6; 15; 102:

Чтобы привести дробь к знаменателю 6, нужно числитель и знаменатель дроби умножить на дополнительный множитель 2:

Чтобы привести дробь к знаменателю 15, нужно числитель и знаменатель дроби умножить на дополнительный множитель 5:

Чтобы привести дробь к знаменателю 102, нужно числитель и знаменатель дроби умножить на дополнительный множитель 34:

Следовательно, правильный ответ:

№ 2. Какое число является наименьшим общим знаменателем дробей и ?

12

24

96

35

Чтобы найти наименьший общий знаменатель дробей и , нужно:

1. разложить на простые множители знаменатели дробей: 8 = 2 ∙ 2 ∙ 2 и 12 = 2 ∙ 2 ∙ 3;
2. найти НОК (8, 12) = 24.

Следовательно, правильный ответ: 24.

В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.

Что такое приведение дроби к общему знаменателю?

Обыкновенные дроби состоят из числителя – верхней части, и знаменателя – нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 1114, 1714, 914 имеют одинаковый знаменатель 14. Другими словами, они приведены к общему знаменателю.

Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.

Очевидно, что дроби 45 и 34 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 45 на 4, а числитель и знаменатель дроби 34  умножим на 5. Вместо дробей 45 и 34 получим соответственно 1620 и 1520.

Приведение дробей к общему знаменателю – это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.

Общий знаменатель: определение, примеры

Что такое общий знаменатель?

Общий знаменатель дробей – это любое положительное число, которое является общим кратным всех данных дробей.

Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.

Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.

Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 16 и 35. Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5. Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.

Рассмотрим пример.

Наименьший общий знаменатель

Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.

Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:

Как привести дроби к наименьшему общему знаменателю

Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.

Рассмотрим применение этого правила на конкретном примере.

Приведение нескольких дробей к наименьшему общему знаменателю

По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.

Приведем еще один пример.

Как привести дробь к наименьшему общему знаменателю (пример)

ПРИВЕДЕНИЕ
ДРОБЕЙ К ОБШЕМУ ЗНАМЕНАТЕЛЮ (3 ч)

Информация
для учителя

Обратить внимание учеников на
разный смысл выражений: «общий знаменатель дробей», «наименьший общий
знаменатель дробей (НОЗ)».

Чтобы привести дробь к новому
знаменателю, надо:

1)      разделить
новый знаменатель на знаменатель данной дроби, в результате получится число,
которое является дополнительным множителем;

2)      умножить
числитель и знаменатель данной дроби на дополнительный множитель. Чтобы найти
наименьший общий знаменатель дробей, надо:

3)      выяснить,
не делится ли знаменатель одной дроби на знаменатель другой дроби. Если да, то
больший знаменатель и будет НОЗ этих дробей;

4)      выяснить,
не являются ли знаменатели данных дробей взаимно простыми числами. Если да, то
произведение этих знаменателей и будет НОЗ этих дробей;

5)      если
не выполняется ни 1, ни 2 пункт, то надо найти наименьшее общее кратное этих
знаменателей. Это число и будет НОЗ этих дробей.

Чтобы привести дроби к наименьшему
общему знаменателю, надо:

1)      найти
НОК знаменателей этих дробей. Оно и будет НОЗ;

2)      найти
дополнительный множитель для каждой дроби;

3)      умножить
числитель и знаменатель каждой дроби на ее дополнительный множитель.

Урок
26. Приведение дробей к общему знаменателю

Цели: ввести понятие дополнительного
множителя; отрабатывать умения приводить дроби к новому знаменателю и находить
дополнительный множитель; закрепить знание основного свойства дроби и умение
сокращать дроби; развивать математическую речь.

Ход урока

I.        
Организационный момент

II.           
Актуализация знаний
учащихся

1.      Ознакомить учащихся с результатами
самостоятельной работы.

2.      Решить задания, в которых
допущено наибольшее количество ошибок.

III.           
Устный счет

1.      Найдите наибольший общий
делитель и наименьшее общее кратное чисел: 9 и 12; 12 и 16; 15 и 25; 3 и 4; 6 и 18; 4 и 15; 12 и 5; 6 и 20; 3 и 7.

2.      Чему равен наибольший общий
делитель двух чисел, если наименьшее общее кратное этих чисел равно их произведению?
(1, так как числа взаимно простые.)

3.     
Восстановите
запись:

4.   Объясните, почему несократимы
дроби

5.      На столе лежало 4 яблока, одно
разрезали пополам. Сколько стало яблок? (4.)

6.      Из двух пунктов, находящихся на
расстоянии 144 км, навстречу друг другу выехали машина и велосипедист. Скорость
машины 60 км/ч, скорость велосипедиста 12 км/ч. Через какое время они
встретятся? (2
ч.)

IV.           
Индивидуальная
работа

1 карточка

1.   Сократите дроби:

2.    Сократите:
;

2 карточка (для сильных учащихся)

1.   Сократите дроби:

2.    Сократите:
;

V.         
Сообщение
темы урока

–       
Сегодня на
уроке мы узнаем, что такое дополнительный множитель дробей, и будем приводить
дроби к новому знаменателю.

VI.           
Изучение
нового материала

1.      Подготовительная работа.

№
286 стр. 47 (устно).

(Ответ:
2, 6, 3, 8, 4.)

–       
Умножьте
числитель и знаменатель дроби на 6:

–       
Какая дробь получилась в результате умножения? (В результате
получается дробь, равная данной, числитель и знаменатель которой кратны
прежней.)

2.      Работа над новой темой.

–     Дана дробь . Умножьте числитель и знаменатель дроби на 2.

–   Какая дробь получилась?

–  Что можно сказать о дробях  и ? (

–       
В таком
случае говорят, что дробь – привели к новому знаменателю 8.

–       
К какому новому знаменателю можно привести данную дробь? (Дробь
можно привести к любому знаменателю, кратному знаменателю данной дроби.)

Определение. Число, на которое надо умножить
знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.

VII.           
Закрепление
изученного материала

1.      № 275 стр. 45 (у доски и в
тетрадях с подробным комментированием).

Что
нужно сначала найти, чтобы привести дроби к новому знаменателю? (Дополнительный множитель.)

Решение:

–       
Изменилась
ли дробь после ее приведения к новому знаменателю? (Мы получили дробь, равную
данной.)

–     Что можете сказать о дробях ? (Это различные записи одного и того же числа.)

2.      № 276 стр. 45 (с
комментированием у доски и в тетрадях).

Решение:

–       
Что интересного заметили? (Числитель новой дроби равен
количеству минут.)

VIII.           
Физкультминутка

IX.           
Работа над задачей

№
292 стр. 47 (после подробного разбора самостоятельно можно предложить решить
любым способом).

–       
Прочитайте
задачу.

–       
Что
известно? Что надо узнать?

–       
Что можно
узнать 1 действием? (Скорость сближения.)

–       
Как найти расстояние,
зная скорость и время? (Скорость умножить на время.)

–       
Можно ли
вторым действием найти расстояние? (Нет.)

–       
Почему? (Скорость и время выражаются разными единицами
измерения.)

–       
В чем надо
выразить 15 мин? (В секундах.)

–       
Сколько
секунд в 1 мин? (60 с.)

–       
Сколько
секунд в 15 мин? (15умножить на 60.)

Решение:

 (км/с) — скорость сближения.

 (с) – до встречи.

 (км)

–       
Как
по-другому можно решить задачу?

–       
Что можно сделать сначала? (Перевести минуты в
секунды.)

–       
Что можно найти потом? (Расстояния, которые пролетят комета
и космический корабль за это время.)

–       
Что узнаем последним действием? (Все расстояние, которое
будет между ними до встречи.)

Решение:

 — до встречи.

 – пролетит комета.

 — пролетит космический корабль.

(Ответ: 72 000 км.)

X.          
Повторение изученного
материала

1.      № 288 стр. 47 (один ученик
решает на обратной стороне доски, остальные — в тетрадях).

–       
Что значит
сократить дробь?

–       
Какая дробь
получается в результате сокращения? (Несократимая, равная данной дроби.)

Решение:

–    
Что интересного заметили? (При
сокращении последних двух дробей
получилась дробь .)

–       
Что можете
сказать о дробях, которые надо было сокращать? (Последние две дроби равны.)

XI.          
Самостоятельная
работа (можно выставить оценки)

Вариант
I

1.      № 253 стр. 40 (записать
промежуточные ответы).

2.      № 294 (1) стр. 47.

3.      № 295 (1,2) стр. 47.

Вариант
II (для
более подготовленных учеников)

1.      № 284 стр. 46 (записать
промежуточные ответы).

2.      № 294 (2) стр. 47.

3.      № 295 (3, 4) стр. 47

XII.           
Подведение
итогов урока

–       
К какому новому знаменателю можно привести данную дробь? (Дробь
можно привести к любому знаменателю, кратному знаменателю данной дроби.)

–    
Можно ли привести дробь  к знаменателю 35? К
знаменателю 25?

–       
Какое число
называют дополнительным множителем?

–       
Как найти
дополнительный множитель?

Домашнее задание

№ 297 (а, б), 300 (а – в), 301, 303 (а) стр. 48.

Цель урока: закрепить основное свойство дроби, научить учащихся применять это свойство на практике приведения к общему знаменателю дробей, показать связь между приведением дробей к общему знаменателю и НОКом знаменателей дробей.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний

Учитель фронтально опрашивает учащихся о основном свойстве дроби. Вспоминают понятие НОКа и способы нахождения НОКа двух чисел:

Поможет нам разобраться с этой темой основное свойство дроби, которое, напомню, звучит следующим образом:

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Так, например, по основному свойству дробь 2/3 можно привести к знаменателю 6, умножив и числитель, и знаменатель на 2. Эту дробь можно привести и к знаменателю 9, и 12, и к любому другому числу, кратному 3.

Напомним, что дроби можно приводить только к тем знаменателям, которые кратны исходным.

Ученики по очереди называют числа, к которым можно привести знаменатель дроби ¾.

Дробь ¾ можно привести к знаменателю 4, 8, 12 и к любому другому числу, кратному 4.

Учитель обращает внимание учеников, что можно обе дроби привести к знаменателю 12.

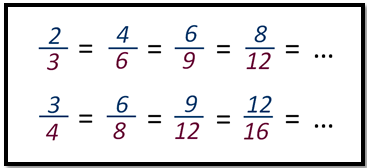
III. Изучение нового материала

Говорят, можно 2/3 и ¾ можно привести к общему знаменателю.

То есть если у нас есть две дроби с разными знаменателями, мы можем сделать так, чтобы знаменатели стали одинаковыми.

Приведение к общему знаменателю понадобится для сложения и вычитания обыкновенных дробей. Кроме того, сравнивать дроби с одинаковыми знаменателями очень просто.

Приведем к общему знаменателю дроби 11/12 и 17/18.

Сначала нам нужно найти такое число, которое делится на каждый из знаменателей.

Учащиеся называют свои варианты чисел.

Таких чисел очень много: 36, 72, 108 и так далее.

Затем приводим к этому числу знаменатели обеих дробей.

То есть дроби можно привести к одинаковому знаменателю 36, 72, 108, 144 и так далее. Удобнее всего выбирать наименьший из возможных общих знаменателей, так как объем вычислений в этом случае будет минимальным.

Например,

11/12=33/36. Чтобы привести 11/12 к знаменателю 36, умножим числитель и знаменатель на 3.

Кстати, число, на которое мы умножаем числитель и знаменатель, называется «дополнительным множителем».

11/12=132/144. Чтобы привести 11/12 к знаменателю 144, умножим числитель и знаменатель на 12. А это немного сложнее, чем умножать на 3.

17/18=34/36. Чтобы привести 17/18 к знаменателю 36, умножим числитель и знаменатель на 2.

17/18=136/144. Чтобы привести 17/18 к знаменателю 144, умножим числитель и знаменатель на 8. Задумались? Поэтому не усложняйте сами себе задачу. Выбирайте наименьший общий знаменатель.

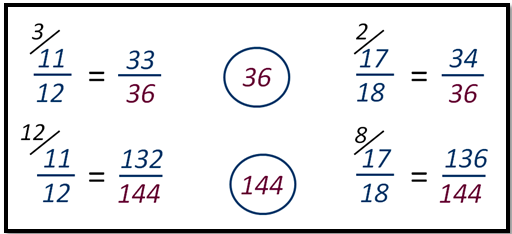
Ученики делают вывод о рациональности приведения дробей к наименьшему общему знаменателю.

Для чисел 12 и 18 число 36 будет наименьшим общим кратным.

IV.Закрепление и практическое применение знаний

В математике существует много способов нахождения общего кратного чисел, а значит общего знаменателя для дробей.

Поэтому, если перед вами стоит задача приведения дробей к общему знаменателю, не торопитесь. Правильно выбранный способ может сократить ваше решение.

Приведем 7/12 и 5/48 к общему знаменателю. Вначале внимательно посмотрите на знаменатели дробей. Возможно, один из них делится на другой.

Ученики делают вывод, то знаменатель 48 делится на 12.

В этом случае дробь с большим знаменателем вообще не надо ни на что умножать. 48 и будет общим знаменателем обеих дробей. А число, полученное в результате деления 48 на 12, будет дополнительным множителем для дроби с меньшим знаменателем.

5/48=5/48

7/12=28/48

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он только в случае, когда один знаменатель делится на другой.

Существует способ, который работает для любых дробей. Суть способа заключается в нахождении наименьшего общего кратного знаменателей. Этот способ используется чаще всего.

Приведем к общему знаменателю дроби 7/410 и 5/861.

Для начала найдём НОК чисел 410 и 861.

Разложим эти числа на простые множители. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь быстро раскладывать на простые множители. Главное — помнить признаки делимости и иметь под рукой таблицу простых чисел.

Теперь записываем все множители одного из чисел, например числа 861. Потом добавляем к ним недостающие множители из разложения другого числа. В этом примере в разложении числа 410 три множителя: 2, 5 и 41. Множитель 41 уже есть в записи, а множителей 2 и 5 нет. Эти недостающие множители мы и добавим к выписанным множителям числа 861.

Наименьшее общее кратное чисел 410 и 861 равно 8610.

Теперь найдем дополнительный множитель для дроби со знаменателем 410. Для этого 8610 делим на 410. Получим 21.

Теперь найдем дополнительный множитель для дроби со знаменателем 861. Для этого 8610 делим на 861. Получим 10.

Последний этап — умножение дробей на дополнительные множители.

Если вам сложно раскладывать числа на множители, находить наименьший общий знаменатель, то следующий способ для вас.

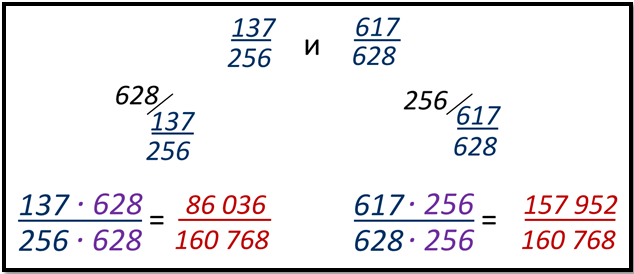
Приведём к общему знаменателю 3/10 и 5/6.

Для этого умножаем первую дробь на знаменатель второй дроби.

3/10=18/60

А вторую — на знаменатель первой.

5/6=50/60

В результате знаменатели обеих дробей стали равными произведению исходных знаменателей.

Этот способ простой для понимания. Но приготовьтесь много считать, если используете этот способ для дробей с большими числами в числителе и знаменателе.

Учитель вместе с учениками проговаривают все возможные способы приведения, все достоинства и недостатки.

№ 275, 278, 283.

V. Подведение итогов урока. Рефлексия

Повторим главное:

Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.

Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.

VI. Домашнее задание

§2, п. 10, № 299, 300.