Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.
Формула площади квадрата.
Площадь квадрата обозначается буквой – S.
Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.
Обычно сторону обозначают буквой – “a”
Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.
Либо может встречаться вот такая формулировка площади квадрата:
Площадь квадрата равна произведению стороны квадрата на себя.

S = a²
Где S – площадь квадрата,
a – длина одной из сторон.
Пример подсчета площади квадрата
Как вычислить площадь квадрата?
Для того, чтобы найти площадь квадрата – нужно знать длину стороны квадрата.
Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!
Пусть это будет 10см.
Условие задачи :
Сколько будет площадь квадрата со стороной 10см.
Решение задачи – найти площадь квадрата:
Как вы помните из правила высчитывания площади квадрата – нужно сторону квадрата умножить на себя или возвести во вторую степень.
S = a²
Умножаем сторону квадрата 10, на себя, на 10 :
10 * 10 = 100см2
Ответ :
Площадь квадрата со стороной 10см, будет равна 100см2
100см2
Как найти площадь квадрата если известен периметр!?
Условие задачи : найдите площадь квадрата, если известен периметр = 32см.
Решение задачи – найти площадь квадрата:
Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:
P = 4a

Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.
И далее по формуле площади квадрата узнаем его площадь :
S = a² = 4² = 16см²
Ответ задачи :
Квадрат, у которого периметр 32 см, площадь равна 16см²
Как найти площадь квадрата если известна диагональ!?
Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.
Решение задачи – найти площадь квадрата:
Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :
a² + a² = d²
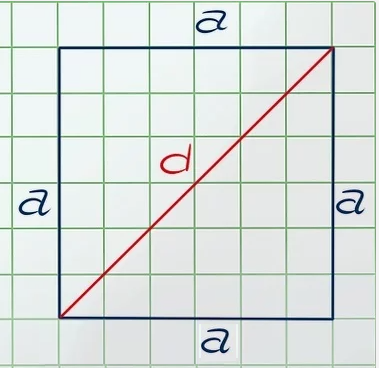
Немного нужно преобразовать :
a² + a² = d² -> 2a² = d² -> a² = d²/2
А если S = a², то S = d²/2
И далее нам нужно подставить нашу диагональ :
S = 8²/2 = 64/2 = 32см².
Ответ :
Если диагональ квадрата равна – 8см, То площадь квадрата равна – 32см².
Какая единица измерения площади квадрата!?
После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : “площадь квадрата почему см2“.
Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?
Мы можем рассказать… о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?
Единица измерения площади квадрата
Единица измерения площади квадрата – может быть, любая мера длины в квадрате.
Если мера длины сантиметр, то площадь будет сантиметр в квадрате – см².
Если мера длины метр, то площадь будет метр в квадрате – м².
Если мера длины километр, то площадь будет километр в квадрате – км². и т.д…
Почему единица измерения площади квадрата пишется с двойкой
Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!
Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?
Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения… то мы увидим откуда берется двойка…
Давайте покажем на примере…
Пусть надо найти площадь квадрата со стороной 12 см.
Так и записываем в формулу :
S = 12см * 12см
Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :
12*12(см*см) = 12²см² = 144см²
Как найти площадь квадрата зная радиус вписанной окружности!?
Задача :
Как найти площадь квадрата зная радиус вписанной окружности!?
Это очень простая задача!
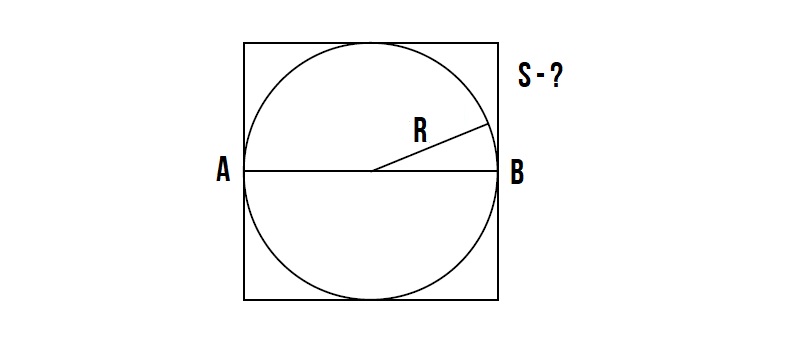
Диаметр вписанной окружности равна стороне квадрата.
Диаметр окружности равен 2R.
Значит сторона квадрата равна 2R.
Далее вспоминаем формулу площади квадрата – S = a², где a – сторона квадрата, которая равна = 2R.
Значит площадь квадрата равна S = (2R)²
Как найти площадь квадрата зная радиус описанной окружности!?
Задача :
Как найти площадь квадрата зная радиус описанной окружности!?
Данная задача такая же простая, как и выше описанная!
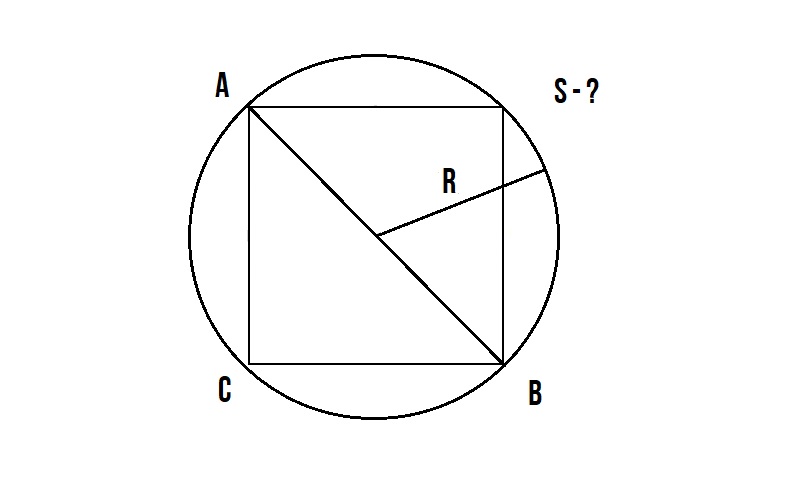
У нас известен радиус окружности описанной вокруг квадрата.
Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.
По диагонали квадрата мы уже один раз высчитывали площадь здесь -> S = d²/2
Далее подставляем S = (2R)²/2
Найти площадь квадрата онлайн
Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :
Сторона квадрата – заполнить значением стороны квадрата.
И нажать кнопку посчитать.
-

1
Write it down. Let’s say you’re working with a square with a side length of 3 centimeter (1.2 in). Write it down.
-

2
Understand the formula for the area of a square(Area=side^2). To calculate the area of any rectangle, you need to multiply its length by width. But since all squares have equal length sides, you can just multiply the distance by itself. If the length of a side of a square is 3 centimeter (1.2 in), then you just have to square 3 centimeter (1.2 in) to find the area of a square. 3 centimeter (1.2 in) x 3 centimeter (1.2 in) = 9 cm2.[1]
Advertisement
-

3
Be sure to state your answer in square units. Then you’re done.[2]
- Squaring the side of a square is the same thing as multiplying the square’s height times its base.
Advertisement
-

1
Take the measurement of the length of the diagonal of the square.
-

2
Understand the formula for the area using a known diagonal. Area = (diagonal^2)/2.[3]
-

3
Multiply the length of this diagonal’s measurement by itself. Square the length of the diagonal. Let’s say you’re working with a square with a diagonal that is 5 centimeter (2.0 in) long. Now, square this number. 5 centimeter (2.0 in) x 5 centimeter (2.0 in) = 25 cm2.
-

4
Divide the current number by 2. Continuing the calculation, 25 cm2 is divided by 2. This gives 12.5 cm2. You’re done.
Advertisement
-

1
Multiply the perimeter by 1/4 to find the length of a side. This is the same as dividing the perimeter by 4. Since there are four sides to a square and each side is of equal length, you can find the length of a square just by dividing the perimeter by 4. Let’s say the perimeter of the square you’re working with is 20 centimeter (7.9 in). Just multiply 20 centimeter (7.9 in) by 1/4: 20 centimeter (7.9 in) x 1/4 = 5 centimeter (2.0 in). You know that the length of a side of the square is 5 centimeter (2.0 in).[4]
-

2
Multiply the length of the side by itself. Square the length of the side. Now that you know that the length of a side is 5 centimeter (2.0 in), you can square it to get the area of the square. Area = (5 cm)2 = 25 centimeter (9.8 in).2[5]
Advertisement
Add New Question
-
Question
If the area of the square is 9 cm, what is the volume of the cube?

Take the square root of 9 and cube it. The answer will be expressed in cm³.
-
Question
What is the formula to calculate the area of an isosceles triangle that has a base and equal sides?

Multiply the length of the base of the triangle by 0.5, and then multiply the length from the base to the highest point of the triangle. A = 0.5 x b x h.
-
Question
A square is 1 cm by 1 cm; what is the area?

Multiply 1 cm by 1 cm: the area is 1 square cm.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
References
About This Article
Article SummaryX
To find the area of a square, use the formula a = side^2, where side is the length of one of the sides of the square. If you only know the perimeter of the square, you can find the area by dividing the perimeter by 4, which will give you the length of each side, and then plugging the side into the formula a = side^2. If you want to learn how to find the area of a square if you only know the length of a diagonal, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 247,873 times.
Reader Success Stories
-

“This article really helped me in my assignment. I answered all of it and got a high score.”
Did this article help you?
Загрузить PDF
Загрузить PDF
Вычислить площадь квадрата очень просто, если вам известна длина стороны, периметр или длина диагонали. Вот, как это можно сделать.
-

1
Запишите длину стороны. Предположим, у вас есть квадрат с длиной стороны 3 см. Запишите это значение.
-

2
Возведите длину стороны в квадрат. Это все, что от вас требуется. Если длина сторон квадрата равна 3 см, то для вычисления площади квадрата нужно просто возвести ее в квадрат: 3 см x 3 см = 9 см2.
-

3
Не забудьте записать ответ в квадратных единицах.
- Возвести сторону в квадрат — это то же самое, что умножить высоту на ширину, так как у квадрата высота и ширина равны.
Реклама
-

1
Измерьте или найдите в условиях длину диагонали квадрата.
-

2
Запомните, как рассчитывается площадь квадрата на основании длины диагонали. Длину диагонали нужно возвести в квадрат и затем разделить на 2: S = (диагональ^2)/2.
-

3
Возведите в квадрат длину диагонали. Предположим, у вас есть квадрат с диагональю 5 см. Возведите ее в квадрат: 5 см x 5 см = 25 см2.
-

4
Теперь разделите результат на 2. 25 см2/2 = 12,5 см2. Площадь нашего квадрата составляет 12,5 см2.
Реклама
-

1
Умножьте периметр на 1/4, чтобы узнать длину стороны. Это то же самое, что разделить его на 4. Поскольку у квадрата четыре стороны равной длины, длину стороны можно узнать, просто разделив периметр на 4. Предположим, вам дан квадрат с периметром 20 см. Умножьте 20 на 1/4: 20 см x 1/4 = 5 см. Теперь мы знаем, что длина стороны составляет 5 см.
-

2
Возведите длину стороны в квадрат. Теперь, когда мы знаем, что длина стороны равна пяти сантиметрам, ее можно возвести в квадрат и получить площадь: (5 см)2 = 25 см2.
Реклама
Об этой статье
Эту страницу просматривали 216 902 раза.
Была ли эта статья полезной?
- Главная
- Справочник
- Как найти площадь квадрата
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь квадрата
Поможем сделать домашку Online
Первое занятие бесплатно
Перейти
Решение задачи по геометрии
Выполнение 1-3 дня
от 150 ₽
Заказать
Подробнее
Контрольные по геометрии
Выполнение 1–4 дня
от 310 ₽
Заказать
Подробнее
Контрольные по математике
Выполнение 1–4 дня
от 260 ₽
Заказать
Подробнее
Содержание:
- Формула
- Примеры вычисления площади квадрата
Формула
Чтобы найти площадь квадрата (рис. 1), надо длину его стороны возвести в квадрат, то есть
$$S=a^2$$
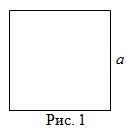
Напомним, что квадратом называется правильный четырехугольник, у которого все стороны и все углы равны.
Примеры вычисления площади квадрата
Пример
Задание. Найти площадь квадрата со стороной 3 см.
Решение. Площадь квадрата равна квадрату его стороны, то есть
$S=3^2=9$(см2)
Ответ. $S=3^2=9$ (см2)
Все формулы площади
Калькулятор площади квадрата

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Узнать стоимость
Пример
Задание. Найти площадь квадрата, диагональ которого равна 2 м.
Решение. Известно, что сторона
$a$ квадрата связана с его диагональю $d$ соотношением:
$$d=a sqrt{2}$$
тогда отсюда находим, что
$a=frac{d}{sqrt{2}}=frac{2}{sqrt{2}}=sqrt{2}$(м)
А тогда искомая площадь
$S=(sqrt{2})^{2}=2$ (м2)
Ответ. $S=2$ (м2)
Читать дальше: как найти площадь прямоугольника.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Поможем выполнить
любую работу
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Контрольные, курсовые, дипломные
Узнать подробнее
Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Краткая теория
- Формулы
- Теоремы
- Свойства
- Таблицы
Теоретический материал
- Формулы и свойства логарифмов
- Таблица интегралов
- Тригонометрические формулы
- Таблица степеней
- Формулы и свойства степеней
- Формулы площади
- Таблица Лапласа
- Формулы объема
Все еще сложно?
Наши эксперты помогут разобраться
Все услуги
Дипломные работы
Выполнение 2-3 недели
от 7000 ₽
Курсовые работы
Выполнение 5-7 дней
от 1500 ₽
Контрольные работы
Выполнение 1–4 дня
от 260 ₽
Написание рефератов
Выполнение 2-5 дней
от 650 ₽
Решение задач
Выполнение 1–3 дня
от 90 ₽
Написание диссертаций
Выполнение 2-3 месяца
от 19 000 ₽
Как найти площадь эллипса
Как найти площадь треугольника
Как найти площадь прямоугольного треугольника
Как найти площадь
Не получается написать работу самому?
Доверь это кандидату наук!
Я даю согласие на обработку своих персональных данных в соответствии с Политикой
конфиденциальности и принимаю условия Договора публичной оферты
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
Прикрепить файл
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
