Узлы электрической цепи как найти – Сайт, где вы сможете решить свои вопросы

Электротехника это точная наука и, как любая наука, не может обойтись без формул. Они нашли отображение в нескольких фундаментальных законах или правилах, один из которых первый закон Кирхгофа.

Он используется при расчётах силы тока в проводах и различных участках электропроводки.

Теория: что такое узел, ветвь, контур

Электрические цепи состоят из ветвей, узлов и контуров.

Ветвь электросхемы

Это основной элемент цепи, на всём протяжении которого протекает один и тот же ток. В простейшем случае это отрезок провода, ветвью так же является электроприбор, включённый в розетку и подходящий к этой розетке кабель.

ветвь электрической цепи

Каждая из ветвей, в свою очередь, может разделяться в узлах на несколько новых ветвей. Ветви могут соединяться между собой параллельно, в узлах, и последовательно. В последнем случае они образуют новую ветвь бОльших размеров.

Узел цепи

Место соединения ветвей в электросхеме называются узлом. Закон Кирхгофа для электрической цепи описывает распределение тока в различных ветвях, подключённых к одному узлу.

что такое узел электрической цепи

первый закон Кирхгофа – узел электрической цепи

Применительно к электропроводке узлом является подключение нескольких проводов к одному автомату или к одной клемме, а так же блок розеток или двойная розетка.

Что такое контур

Все электрические сети включают в себя источник тока. В электрическом фонарике это батарейка и весь контур прослеживаются визуально, а в системе электроснабжения жилого дома им является трансформаторная подстанция, которая может находиться за несколько километров.

контур электрической цепи

В таких сетях мощность источника тока многократно превышает мощность квартирной проводки, поэтому при проектировании электропроводки параметры трансформатора не учитываются и расчёт производится только для цепи, включающей в себя несколько узлов.

Определение

Первый закон Кирхгофа для электрической цепи основан на законе сохранения заряда или на законе сохранения энергии. Согласно этим законам количество “электричества”, приходящее в узел, должно быть равно уходящему из него.

Поэтому у этого правила есть две формулировки:

№1. Алгебраическая сумма токов в узле равна нулю. Это алгебраическая сумма, в которой положительное значение “+” имеет ток направленный в точку узла, а отрицательное значение “-“, это ток отходящий от узла. Такая формула применяется при расчётах сложных схем.
№2. Сумма токов, втекающих в узле равна сумме токов вытекающих из узла. Это арифметическая сумма, без учёта знака величины.

формула по первому закону Кирхгофа

Важно! В сетях переменного тока, особенно высокой частоты, имеются потери, связанные с ёмкостью линии. Величину этих потерь невозможно измерить прямыми методами, что приводит к кажущемуся нарушению первого правила Кирхгофа.

Формула первого правила Кирхгофа

Как и любой другой закон электротехники 1 закон Кирхгофа выражается формулой, имеющей два варианта написания. Для примера можно взять узел с двумя входящими проводами и токами в них I1 и I2 и тремя отходящими I3, I4 и I5:

Алгебраическая сумма. Получается преобразованием предыдущей формулы Σk-Σm=0 или I1+I2-I3-I4-I5=0. Это выражение применяется при сложных расчётах электронных схем.
Арифметическая сумма. Σk=Σm или I1+I2=I3+I4+I5. Здесь k – подходящие линии, а m – отходящие. Такая формула используется при определении сечения токопроводящих жил для однофазной электропроводки или однолинейной схемы систем электроснабжения, а так же необходимой мощности блоков питания.

схема первого закона Кирхгофа – уравнение

Такие уравнения составляются для каждого узла сети, причём нижестоящий узел является ветвью для вышестоящего. Это видно при составлении однолинейной схемы.

Информация! Ток в подходящих проводах считается положительным, а в отходящих отрицательным.

Для трёхфазной сети

Чаще всего трёхфазные сети переменного тока выполняются по схеме с рабочей нейтралью. При этом место соединения фазных проводов с нолём является узлом и подчиняется первому правилу Кирхгофа, однако эта формула имеет более сложный вид.

Дело в том, что в сетях переменного тока кроме активного протекает реактивный, индуктивный или ёмкостной ток. В результате ток в проводах разных фаз сдвинут не на 120°, а на другую величину.

Для расчётов в таких сетях вычерчивается векторная диаграмма и при вычислении величины тока в нейтрали складывается не величина тока, а соответствующий вектор ↑In=↑Ia+↑Ib+↑Ic.

Из-за сложности такого расчета, как правило, он не выполняется, а вместо него производится максимально равномерное распределение нагрузки по фазам, а сечение нейтрального проводника не выбирается, а используется предлагаемое производителями кабельно-проводниковой продукции.

Расчеты электрической цепи с помощью первого закона Кирхгофа

Первый закон Кирхгофа используется для расчёта силы тока и сечения проводов электропроводки и мощности блоков питания.

Расчёт электропроводки

Электропроводка и линии электроснабжения имеют форму дерева – кабель с бОльшим сечением и силой тока делится в узле на несколько ветвей с меньшим сечением и силой тока. При этом Iвх=ΣIвых.

закон Кирхгофа для электрической цепи

Например, при подключении к линии электроприборов с номинальным током 5 А, 4 А и 2 А ток в подходящем кабеле составит Iвх=5+4+2=11А.

Расчёт блока питания

Большинство электроприборов подключаются непосредственно к сети переменного тока 220 В, но есть аппараты, которым необходимо пониженное напряжение. Такие устройства присоединяются к блокам питания.

Например, имеются два источника постоянного напряжения 12 В с силой тока 1,5 А и 2,5 А. Необходимо узнать, какую светодиодную ленту можно подключить к этим устройствам, если их включить параллельно.

Этот расчёт производится по формуле Iвых=ΣIвх=1,5А+2,5А=4А. Следовательно, ток потребления этой ленты может быть не более 4 А или 48 Вт.

Вывод

Первый закон Кирхгофа определяет связь между силой тока в подходящих и отходящих проводах одного узла. Электрический ток это направленное движение заряженных частиц и, согласно закону сохранения массы и энергии, сколько этих элементов подходит, столько же и должно отходить.

Этот закон используется при расчёте сечения токопроводящих жил и мощности источника питания.

первое правило Кирхгофа

Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал. Спасибо за лайк 👍!

#закон Кирхгофа #правило Кирхгофа #электрика

Источник

ads

Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.

Простым языком электрическая схема это упрощенное изображение электрической цепи.

Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.

Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.

В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.

Безымянный - копия (2) - копия

Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.

Ветви присоединённые к одной паре узлов называются параллельными.

Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.

Узел – место соединения трёх и Безымянный - копия (3) - копия более ветвей.

Узел A
Узел B
Узел C
Узел D

Точки К и Е не являются узлами.

Источник

Содержание

Что такое электрическая схема, ветвь, узел, контур.
Методы расчета сложных электрических цепей
Методы расчета сложных электрических цепей
Метод непосредственного применения законов Кирхгофа
Метод контурных токов
Метод узловых потенциалов

Что такое электрическая схема, ветвь, узел, контур.

Простым языком электрическая схема это упрощенное изображение электрической цепи.

Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.

Ветви присоединённые к одной паре узлов называются параллельными.

Узел – место соединения трёх и более ветвей.

Точки К и Е не являются узлами.

Источник

Методы расчета сложных электрических цепей

Сложной электрической цепью называют разветвленную цепь с несколькими источниками электрической энергии. Применение методов эквивалентных преобразований в таких цепях, как правило, не эффективно, так как не позволяют упростить ее до одноконтурной цепи или цепи с двумя узлами. Для расчета таких цепей используют более общие методы.

Метод непосредственного применения законов Кирхгофа

Метод заключается в составлении системы уравнений с применением первого и второго законов Кирхгофа для заданной электрической цени, решение которой позволяет определить токи всех ветвей цепию.

Реализация этою метода, как и любого другого метода расчета сложной электрической цени, начинается с предварительного анализа ее схемы с целью определения числа узлов 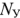, числа ветвей 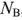, числа независимых контуров 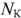, числа ветвей 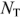с источниками токов, выяснения возможности упрощения схемы.

Прежде всего определяют число неизвестных токов, которое равно 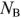— 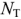. Для каждой ветви задают положительное направление тока.

Далее по первому закону Кирхгофа составляют 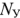— 1 независимых уравнений.

Затем по второму закону составляют 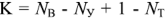уравнений. При этом выбирают независимые контуры, не содержащие источников тока.

Общее число составленных по первому и второму законам Кирхгофа должно быть равно числу 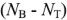неизвестных токов.

Рассмотрим применение законов Кирхгофа для определения токов в ветвях цепи, схема которой приведена на рис. 1.25. Пусть ЭДС идеальных источников напряжения 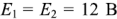, сопротивления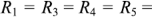 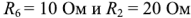. Требуется определить все токи схемы с помощью метода непосредственного применения законов Кирхгофа.

Схема содержит 6 ветвей с неизвестными токами и четыре узла. Па схеме узлы обозначены арабскими цифрами, показаны принятые направления токов и направления обхода контуров А, Б и В.

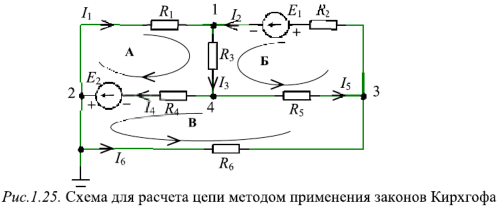
Составим систему из 6 уравнений. Уравнения по первому закону Кирхгофа запишем для узлов 1, 2, 3, уравнения по второму закону Кирхгофа запишем для контуров А, Б, В:

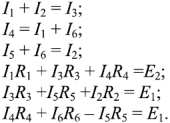
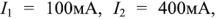
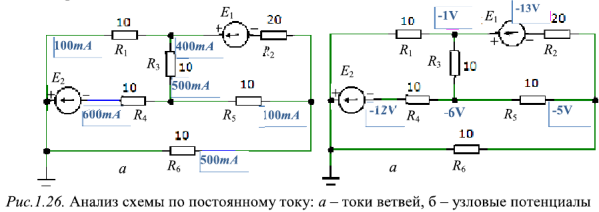
Решив эту систему уравнений, получим 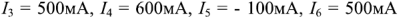. Отрицательное значение тока 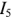, указывает на то, что выбранное при составлении уравнений направление этого тока не соответствует действительности. Правильное направление — от узла 3 к узлу 4.

Для проверки вычислений с помощью программы схемотехнического моделирования Micro Сар выполнен анализ по постоянному току схемы, изображенной на рис. 1.25. Изображенные на рис. 1.26,а значения токов ветвей (в мА) подтверждают правильность выполненных расчетов. Изображенные на рис. 1.26,б узловые потенциалы схемы (в В) позволяют определить направление токов ветвей.

Метод контурных токов

Метод контурных токов наиболее часто применяется на практике для расчета сложных цепей, так как он позволяет находить все неизвестные величины при числе уравнений, меньшем числа неизвестных величин.

По этому методу в каждом независимом контуре схемы вместо действительных токов в ветвях вводят условный контурный ток. Действительный ток в любой ветви, принадлежащей только одному контуру, численно равен контурному току. Действительный ток в любой ветви, принадлежащей нескольким контурам равен алгебраической сумме контурных токов, проходящих через эту ветвь.

Уравнения для расчета контурных токов составляются по второму закону Кирхгофа. При этом учитываются напряжения на всех пассивных элементах контура от собственного контурного тока и в смежных элементах -от контурных токов соседних контуров. Направление контурного тока в независимом контуре выбирают произвольно. Направление обхода контура обычно выбирают совпадающим с направлением собственного контурного тока.

Падение напряжения при прохождении тока смежного контура в элементе принимают положительным, если направление тока в смежном контуре совпадает с направлением обхода, Если направление тока смежного контура не совпадает с направлением обхода, падение напряжения считают отрицательным. Значение ЭДС берется со знаком плюс, если направление обхода контура совпадает с положительным направлением ЭДС, и со знаком минус — если не совпадает.

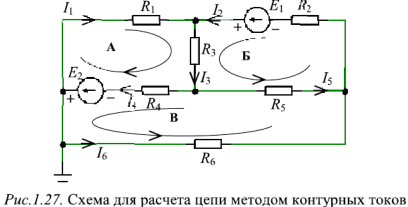
Метод контурных токов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.27. Схема имеет три независимых контура: А, Б, В. Через сопротивления каждого контура проходит свой контурный ток 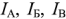. Направления обхода каждого контура совпадает с направлением контурного тока этого контура. ЭДС идеальных источников напряжения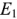 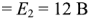, сопротивления 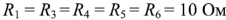и .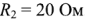

Уравнения, составленные по второму закону Кирхгофа, для контуров А, Б и В:

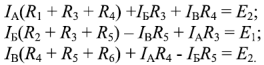
Подставив в эту систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим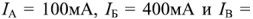

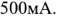
Действительные токи ветвей схемы:

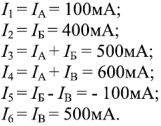
Полученные значения полностью совпадают с результатами ранее проделанного расчета этой же цени по методу непосредственного применения Законов Кирхгофа.

Метод узловых потенциалов

Потенциал любой точки электрической цепи определяется напряжением между данной точкой и точкой цепи с потенциалом равным нулю.

Метод узловых потенциалов заключается в том, что вначале полагают равным нулю потенциал некоторого базисного узла и для оставшихся ( 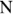-1) узлов составляют уравнения по первому закону Кирхгофа: алгебраическая сумма токов всех ветвей, подключенных к рассматриваемому узлу равна нулю. При этом токи ветвей, соединяющих узлы, определяются с помощью обобщенного закона Ома. Решив полученную систему уравнений, определяют потенциалы узлов.

Далее, применив обобщенный закон Ома для ветвей, определяют искомые токи.

Метод узловых потенциалов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.28 (я). В этой схеме ЭДС идеальных источников напряжения 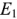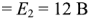, сопротивления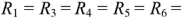 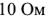и .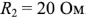

Схема имеет четыре узла. Примем потенциал узла 3 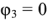. Составляем уравнения по методу узловых потенциалов. Сумма токов узла 1 приравнивается нулю. Ток каждой ветви, подключенной к узлу 1, записывается в соответствии с обобщенным законом Ома

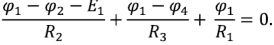
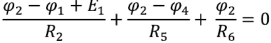
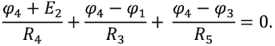
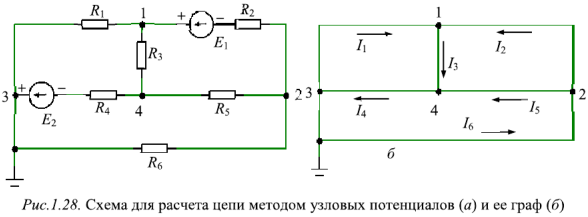
Подставив в полученную систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим 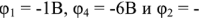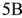. Полученные результаты совпадают с данными (рис. 1.26,6^, полученными при выполнении с помощью программы Micro-Сар анализа по постоянному току схемы, изображенной на рис. 1.28,а.

Применив обобщенный закон Ома для каждой ветви схемы, получим искомые токи:

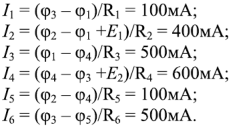
Полученные значения токов совпадают с результатами расчета этой цепи методом непосредственного применения законов Кирхофа и методом контурных токов.

Направления найденных токов указаны на графе цепи на рис. 1.28,6. Графом цепи называют такое изображение схемы электрической цепи, в котором все ветви заменены линиями, источники напряжения закорочены, а источники тока разомкнуты. Все ветви и все узлы сохраняются.

Метод узловых потенциалов имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа.

Метод двух узлов является частным вариантом метод узловых потенциалов. Он применяется в тех случаях, когда анализируемая схема содержит только два узла (для определенности узлы 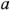и 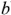) и большое число параллельных ветвей, содержащих и не содержащих источники ЭДС. Согласно методу двух узлов межузловое напряжение

где 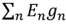— алгебраическая сумма произведений ЭДС ветвей (ЭДС считаются положительными, если они направлены к узлу 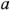, и отрицательными, если от узла 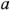к узлу 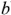) на проводимости этих ветвей; 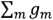— сумма проводимости всех ветвей, соединяющих узлы 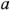и .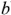

Эта теория взята со страницы помощи с заданиями по электротехнике:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Источник

8. Топологические элементы схемы: ветви, узлы, контуры.

Электрическая
схемапредставляет собой графическое
изображение электрической цепи. Она
показывает как осуществляется соединение
элементов рассматриваемой электрической
цепи.

«Электрическими»
элементами схемы служат активные и
пассивные элементы цепи.

«Геометрическими»
элементами схемы являются ветви и узлы.

Ветвь
– участок схемы, расположенный между
двумя узлами и образованный одним или
несколькими последовательно соединенными
электрическими элементами цепи (рис.
11).

Рис. 11. Изображение
ветвей электрической схемы.

Под последовательным
соединением
элементов цепи понимается такое их
соединение, при котором через все эти
элементы проходит один и тот же ток.

Узел
– место соединения трех или большего
числа ветвей. Место соединения двух
ветвей рассматривается как устранимый
узел.

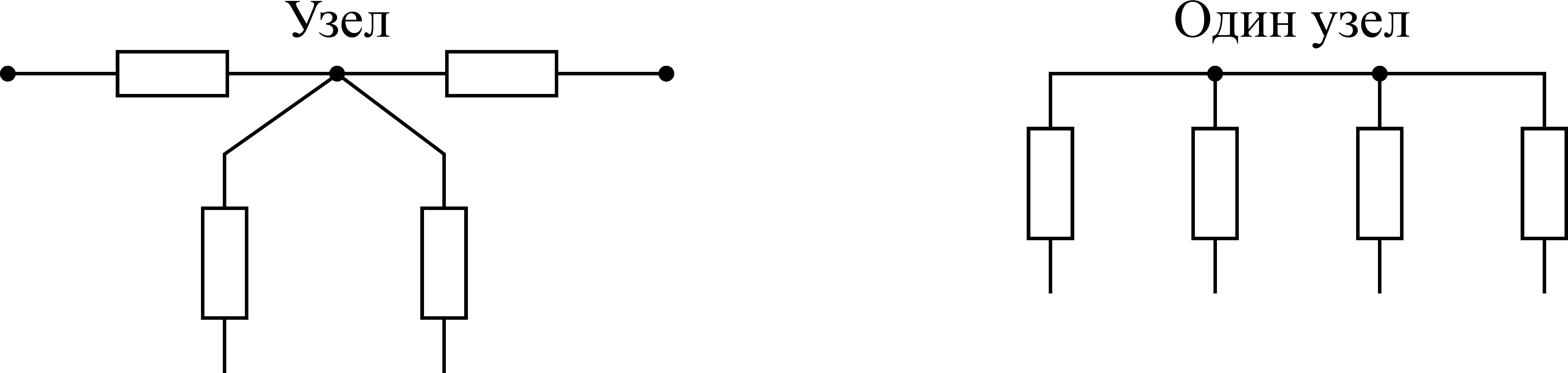
Рис. 12. Изображение
узла электрической схемы.

Ветви присоединенные
к одной паре узлов называются параллельными
(рис. 13).

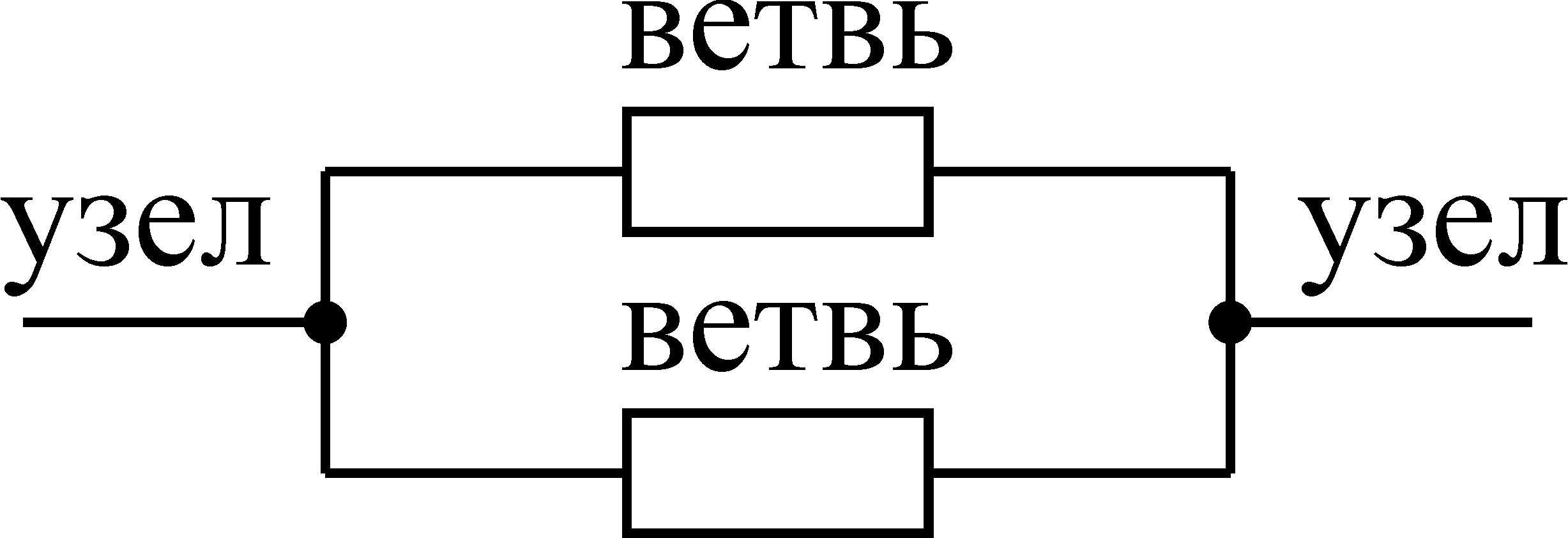
Рис. 13. Параллельное
соединение двух ветвей.

На рис. 14 изображена
электрическая схема пять ветвей и три
узла.

Стрелкой на рис.
указано направление обхода одного из
контуров.

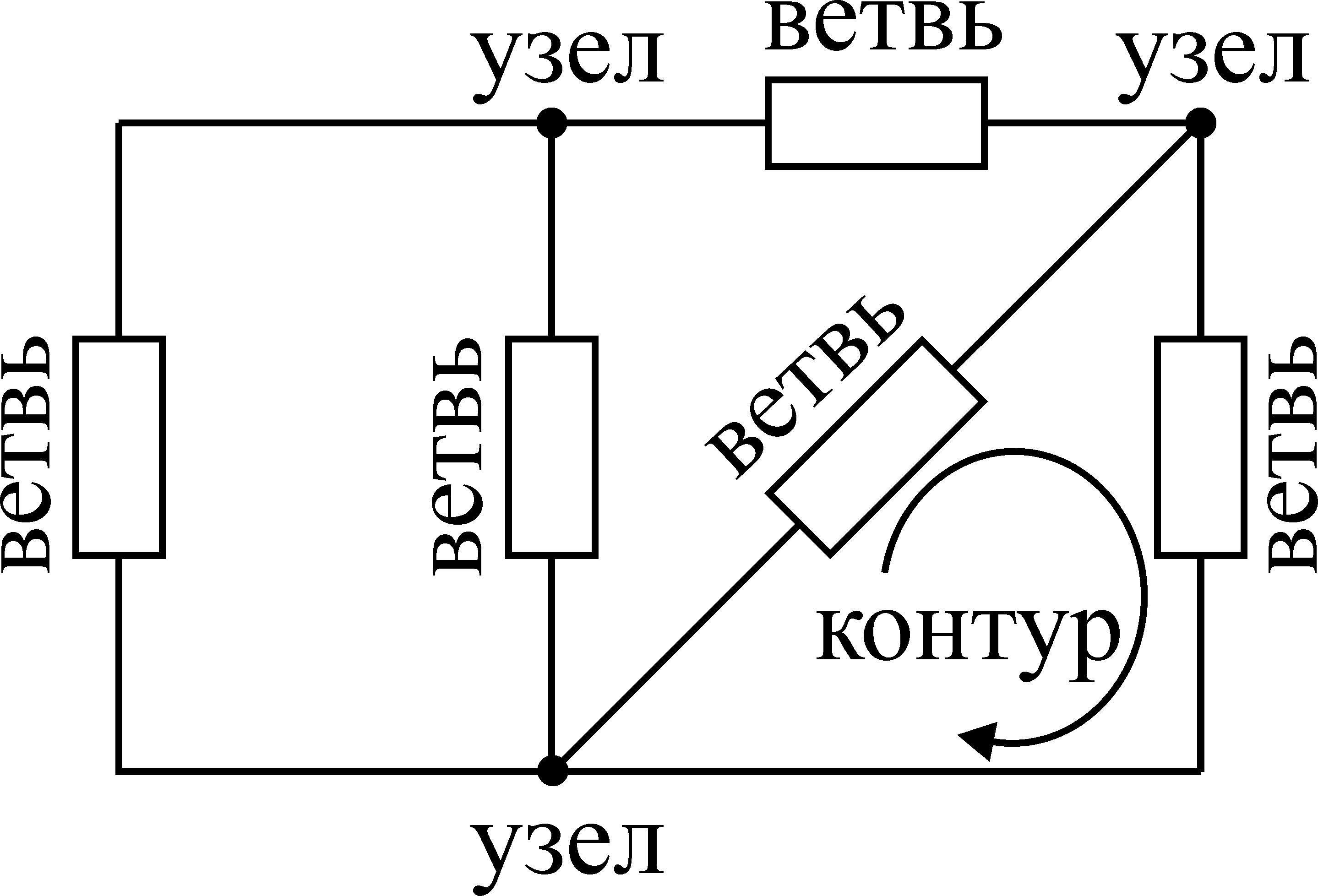
Рис. 14. Схема
электрической цепи.

Под контуром
понимается любой замкнутый путь,
проходящий по нескольким ветвям.

В зависимости от
числа контуров, имеющихся в схеме,
различают многоконтурные и одноконтурные
схемы.

Одноконтурная
замкнутая схема показана на рис. 15.

Одноконтурная
схема является простейшей.

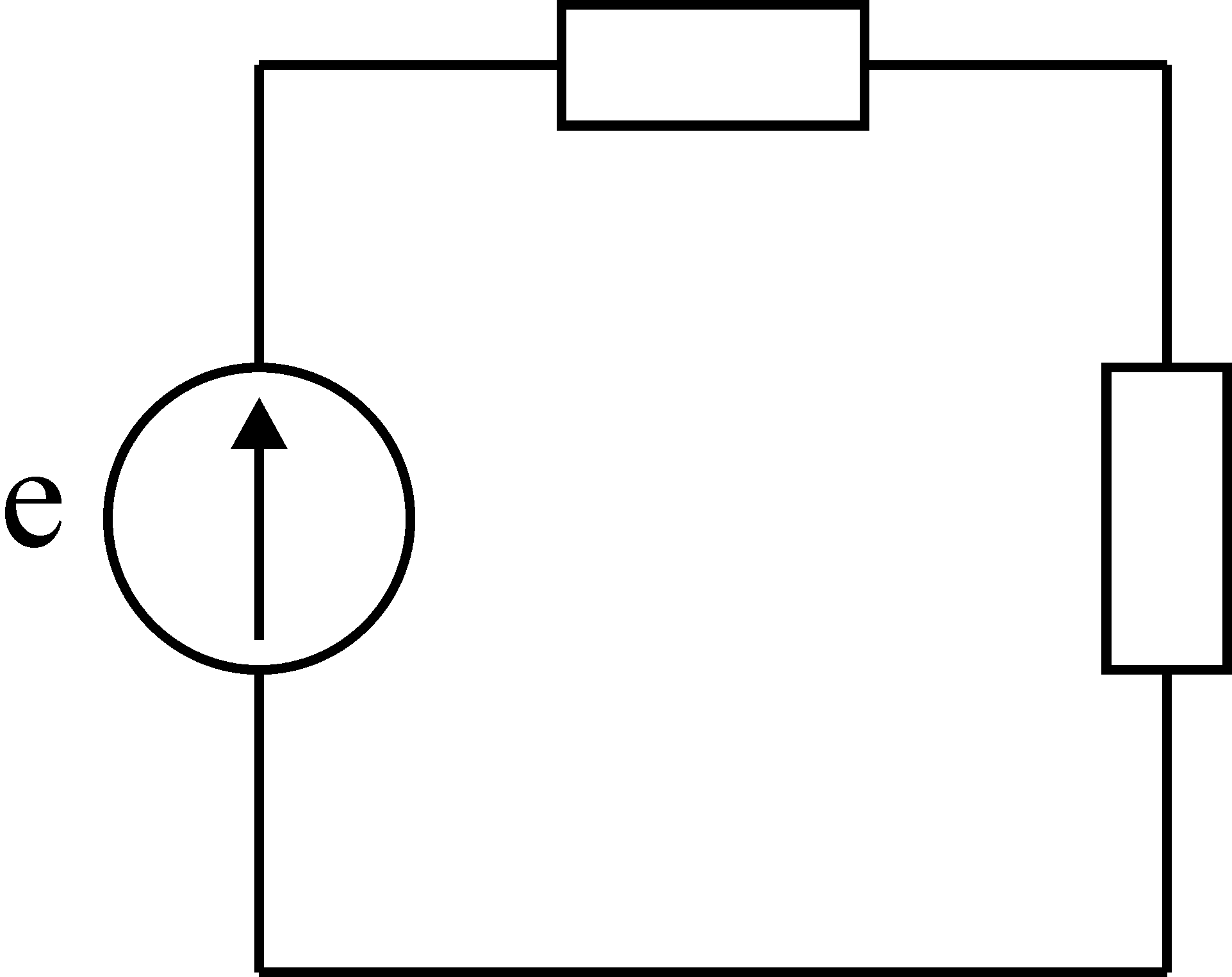
Рис. 15. Одноконтурная
схема.

9. Распределение потенциала вдоль участка ветви. Потенциальная диаграмма.

Рассмотрим участок
электрической цепи (рис. 16)

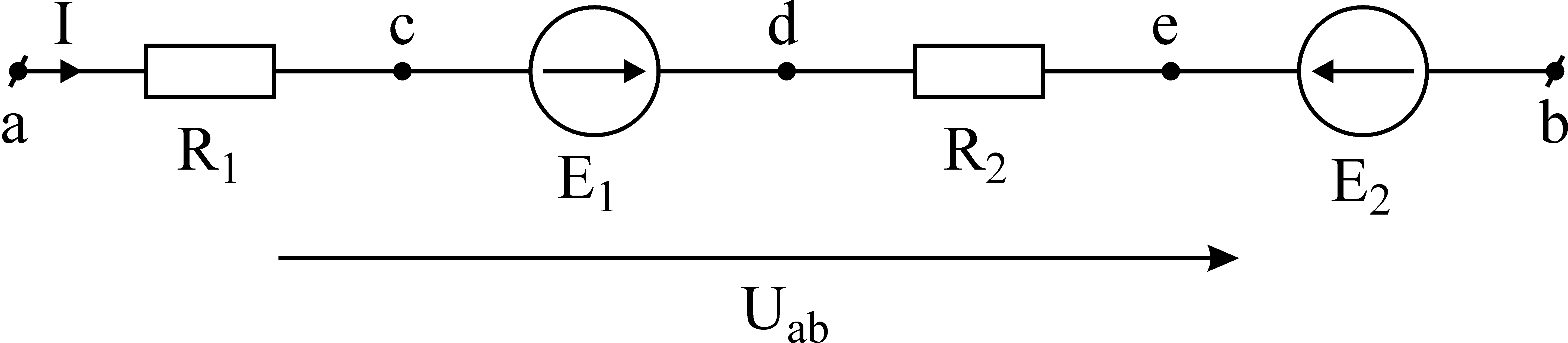
Рис. 16.

Участок ветви,
содержащий один или несколько источников
энергии, является активным.

Положительные
направления тока и напряжения указаны
стрелкой.

Определим потенциалы
точек c,
d,
e,
b,
предположив, что известен потенциал
точки a-_a.

Для правильного
выбора знаков следует
помнить,
что:

ток в сопротивлении
всегда направлен от более высокого
потенциала к более низкому, т.е. потенциал
падает по направлению тока.
э.д.с., направленная
от точки «с» к точке «d»,
повышает потенциал последней на величину
E.
напряжение U=Uac
положительно, когда потенциал точки а
выше, чем потенциал точки с.

При обозначении
напряжения (разности потенциалов) на
схемах посредством стрелки она ставится
в направлении от точки высшего потенциала
к точке низшего потенциала.

На рис. 16 ток
протекает от точки «а» к точке «с»,
значит потенциал _с
будет меньше _aна величину
падения напряжения на сопротивлении
R₁,
которое по закону Ома равно IR₁:

_{с =}_a– IR₁

На участке cd
э.д.с. E₁
действует в сторону повышения потенциала,
следовательно:

_d=
_с₊E_1

=_a–
IR₁₊E₁

Потенциал точки
«e»
меньше потенциала точки «d»
на величину падения напряжения на
сопротивлении R₂:

_e=
_d–
IR_{2

=}_a–
IR₁₊E₁–
IR₂

На участке e
в э.д.с. E₂действует
таким образом, что потенциал точки «b»
меньше потенциала точки «e»
на величину E₂:

_b=
_e–E_2

=_a–
IR₁₊E₁–
IR₂–E₂
= _a
– I(R₁+R₂)
+ E₁-E₂
(15)

Чтобы наглядно
оценить распределение потенциала вдоль
участка цепи, полезно построить
потенциальную диаграмму, которая
представляет график изменения потенциала
вдоль участка цепи или замкнутого
контура.

По оси абсцисс
графика откладываются потенциалы точек,
а по оси ординат – сопротивления
отдельных участков цепи. Для участка
цепи рис. 16 распределение потенциала
построено на рис. 17.

Рис. 16. Потенциальная
диаграмма участка цепи.

Потенциальная
диаграмма рис. 16 построена, начиная с
точки a,
которая условно принята за начало
отсчета. Потенциал _aпринят
равным нулю.

Точка цепи, потенциал
которой условно принимается равным
нулю, называется базисной.

Если в условии
задачи не оговорено, какая точка является
базисной, то можно потенциал любой точки
условно приравнивать к нулю. Тогда
потенциалы всех остальных точек будут
определяться относительно выбранного
базиса.

Соседние файлы в папке Конспект 2

Источник

Введём понятие узла. Узел – точка цепи, в которой сходится не менее трёх проводников.

Тогда разветвлённой цепью назовём цепь, имеющую один или более узлов.

Для расчёта таких цепей используются два правила Кирхгофа.

Первое правило Кирхгофа

Рис. 1. Первое правило Кирхгофа

Первое правило Кирхгофа: сумма токов, входящих в узел, равна сумме токов, выходящих из узла (рис. 1). A — узел в цепи постоянного тока. Путь в цепи протекают токи $displaystyle {{I}_{4}}$ — $displaystyle {{I}_{4}}$ . Тогда, исходя из первого правила Кирхгофа:

$displaystyle {{I}_{1}}+{{I}_{4}}={{I}_{2}}+{{I}_{3}}$

Или, обобщая:

$displaystyle sumlimits_{i}{{{I}_{i}}}=sumlimits_{j}{{{I}_{j}}}$ (1)

Второе правило Кирхгофа (цепь)

Рис. 2. Второе правило Кирхгофа (цепь)

Второе правило Кирхгофа касается такого понятия как контур. Назовём контуром замкнутый участок цепи, содержащий любые элементы цепи. Для визуализации правила введём произвольную цепь с узлами (рис. 2). Пусть наша цепь содержит резисторы $displaystyle {{R}_{3}}$ — $displaystyle C$ , конденсатор ёмкостью $displaystyle {{varepsilon }_{1}}$ и два источника ЭДС $displaystyle {{varepsilon }_{2}}$ , $displaystyle {{r}_{1}}$ с собственными внутренними сопротивлениями $displaystyle {{r}_{2}}$ и $displaystyle {{r}_{2}}$ соответственно.

Второе правило Кирхгофа (Контур)

Рис. 3. Второе правило Кирхгофа (Контур)

По нашей схеме нарисуем контуры (рис. 3). В цепе можно выделить 3 контура обхода: для определённости, красный, синий и зелёный.

Расставим токи для каждого из элементов, обладающих сопротивлением (рис. 4). Направление силы тока выбираем случайным образом.

Второе правило Кирхгофа (Сила тока)

Рис. 4. Второе правило Кирхгофа (Сила тока)

Тогда второе правило Кирхгофа — сумма падений напряжений на каждом из элементов контура равно сумме ЭДС в этом контуре.

Учитывая закон Ома для участка цепи:

displaystyle U=IR (2)

Тогда второе правило Кирхгофа формульно:

$displaystyle sumlimits_{i}{{{I}_{i}}{{R}_{i}}=sumlimits_{j}{{{varepsilon }_{j}}}}$ (3)

Тогда составим второе правило Кирхгофа для контуров на рис. 3 при нескольких условиях:

ток считать положительным при совпадении направления обхода и отрицательным при несовпадении;
ЭДС считать положительным при направлении обхода совпадающим с генерацией тока в источнике (от плюса к минусу) и отрицательным в обратном случае.

Итак, зелёный контур:

$displaystyle {{I}_{5}}{{r}_{1}}+{{I}_{3}}{{R}_{3}}-{{I}_{2}}{{R}_{2}}={{varepsilon }_{1}}$ (4)

Для синего контура:

$displaystyle -{{I}_{1}}{{R}_{1}}+{{I}_{4}}{{r}_{2}}-{{U}_{c}}-{{I}_{2}}{{R}_{2}}={{varepsilon }_{2}}$ (5)

Для красного контура:

$displaystyle {{I}_{1}}{{R}_{1}}+{{I}_{5}}{{r}_{1}}+{{I}_{3}}{{R}_{3}}+{{U}_{c}}-{{I}_{4}}{{r}_{2}}={{varepsilon }_{1}}-{{varepsilon }_{2}}$ (6)

Вывод: правила Кирхгофа (1) и (3) можно использовать для любого вида цепей, однако наибольшую пользу они приносят в случае разветвлённых цепей, в которых есть узлы. При использовании правил необходимо опираться на следующие идеи:

ищем узлы и расписываем первое правило Кирхгофа (1) для каждого из них (часть уравнений может получится одинаковым);
по количеству получившихся уравнений и неизвестных узнаём количество добавочных уравнений;
определяем контур (или несколько), который будем использовать во втором правиле Кирхгофа (3);
задаём направление обхода в контуре (произвольно);
обозначаем токи на каждом из элементов, имеющих сопротивление (направление тока выбираем произвольно);
записываем второе правило Кирхгофа для контура (условия выше).

Источник

Теория: что такое узел, ветвь, контур

Ветвь электросхемы

Узел цепи

Что такое контур

Определение

Формула первого правила Кирхгофа

Для трёхфазной сети

Расчеты электрической цепи с помощью первого закона Кирхгофа

Расчёт электропроводки

Расчёт блока питания

Вывод

Что такое электрическая схема, ветвь, узел, контур.

Методы расчета сложных электрических цепей

Методы расчета сложных электрических цепей

Метод непосредственного применения законов Кирхгофа

Метод контурных токов

Метод узловых потенциалов

8. Топологические элементы схемы: ветви, узлы, контуры.

9. Распределение потенциала вдоль участка ветви. Потенциальная диаграмма.

Вам также может понравиться

Как можно найти электронный билет

Как найти канал на твиче который смотрел

Как составить платежный календарь на месяц

Добавить комментарий Отменить ответ