В четырехугольник вписана окружность как найти площадь

В четырехугольник вписана окружность как найти площадь

Площади четырехугольников

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
ha – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
ha – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник Рисунок Формула площади Обозначения
Прямоугольник S = ab
Параллелограмм
Квадрат S = a 2
S = 4r 2
Ромб
Трапеция
S = m h
Дельтоид S = ab sin φ
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

,

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник
Параллелограмм
Квадрат
S = a 2

где
a – сторона квадрата
S = 4r 2
Ромб
Трапеция
Дельтоид

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник
Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

,

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

Окружность, вписанная в четырехугольник

Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.

На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.

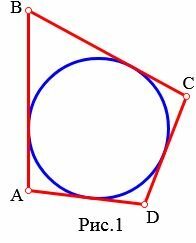
Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.

Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).

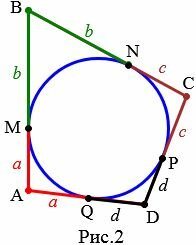
Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то

( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d )

( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, ) (1)
( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. ) (2)

Из равенств (1) и (2), следует:

( small AB+CD=AD+BC. )

Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.

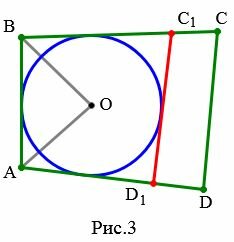
Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.

Пусть эта окружность не касается стороны CD. Тогда возможны два случая.

Случай 1. Сторона CD не имеет общих точек с построенной окружностью.

Проведем касательную C1D1 к окружности, параллельно стороне CD четырехугольника.

Тогда окружность с центром O вписан в четырехугольник ABC1D1. Следовательно, по теореме 1, имеем:

( small AB+C_1D_1=AD_1+BC_1. ) (3)

Но по условию данной теоремы:

( small AB+CD=AD+BC. ) (4)

Вычтем из равенства (4) равенство (3):

( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 )

( small CD-C_1D_1=DD_1+CC_1 )

( small CD=DD_1+CC_1+C_1D_1)

Получили, что в четырехугольнике CC1D1D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).

Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.

Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).

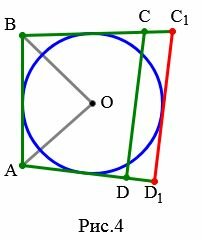
Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.

Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

  • Треугольник
  • Выпуклый, правильный многоугольник
  • Квадрат
  • Равнобедренная трапеция
  • Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

  1. В любой треугольник может быть вписана окружность, причем только один раз.
  2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
  3. Вписанная окружность касается всех сторон треугольника.
  4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

  • Центр окружности вписанной в треугольник равноудален от всех сторон.
  • Точка касания — это точка, в которой соприкасается
    окружность и любая из сторон треугольника.
  • От центра вписанной окружности можно провести
    перпендикуляры к любой точке касания.
  • Вписанная в треугольник окружность делит стороны
    треугольника на 3 пары равных отрезков.
  • Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
    Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

    с — расстояние между центрами вписанной и описанной окружностей треугольника.
    R — радиус описанной около треугольника.
    r — радиус вписанной окружности треугольника.

    В четырехугольник

    1. Не во всякий четырехугольник можно вписать окружность.
    2. Если у четырехугольника суммы длин его противолежащих
      сторон равны, то окружность, может быть, вписана (Теорема Пито).
    3. Центр вписанной окружности и середины двух
      диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
    4. Точка пересечения биссектрис — это центр вписанной окружности.
    5. Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон четырехугольника.
    6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

    [ S = frac<1><2>(a+b+c+d)cdot r = pr ]

    p — полупериметр четырехугольника.
    r — радиус вписанной окружности четырехугольника.

  • Точка касания вписанной окружности, которая лежит на любой из сторон,
    равноудалены от этой конца и начала этой стороны, то есть от его вершин.

    • Примеры вписанной окружности

    Примеры описанного четырехугольника:
    равнобедренная трапеция, ромб, квадрат.

    Примеры описанного треугольника:
    равносторонний    , равнобедренный,
    прямоугольный треугольники.

    Верные и неверные утверждения

    1. Радиус вписанной окружности в треугольник и радиус вписанной
      в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
    2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
    3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
    4. В любой ромб можно вписать окружность. Верное утверждение.
    5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
    6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
    7. Угол вписанный в окружность равен соответствующему центральному
      углу опирающемуся на ту же дугу. Неверное утверждение.
    8. Радиус вписанной окружности в прямоугольный треугольник равен
      половине разности суммы катетов и гипотенузы. Верное утверждение.
    9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
    10. Вписанная окружность в треугольник имеет в общем
      три общие точки со всеми сторонами треугольника. Верное утверждение.

    Окружность вписанная в угол

    Окружность вписанная в угол — это окружность, которая
    лежит внутри этого угла и касается его сторон.

    Центр окружности, которая вписана в угол,
    расположен на биссектрисе этого угла.

    К центру окружности вписанной в угол, можно провести,
    в общей сложности два перпендикуляра со смежных сторон.

    Длина диаметра, радиуса, хорды, дуги вписанной окружности
    измеряется в км, м, см, мм и других единицах измерения.

    [spoiler title=”источники:”]

    http://matworld.ru/geometry/okruzhnost-vpisannaya-v-chetyrekhugolnik.php

    http://colibrus.ru/vpisannaya-okruzhnost/

    [/spoiler]

    Источник

    Как найти площадь четырехугольника

    Как найти площадь четырехугольника

    При решении планиметрических заданий курса геометрии нередко встречается фигура с 4-мя сторонами. Да, речь идет о четырехугольнике. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
    Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.

    1

    Как найти площадь четырехугольника

    Многоугольник произвольный

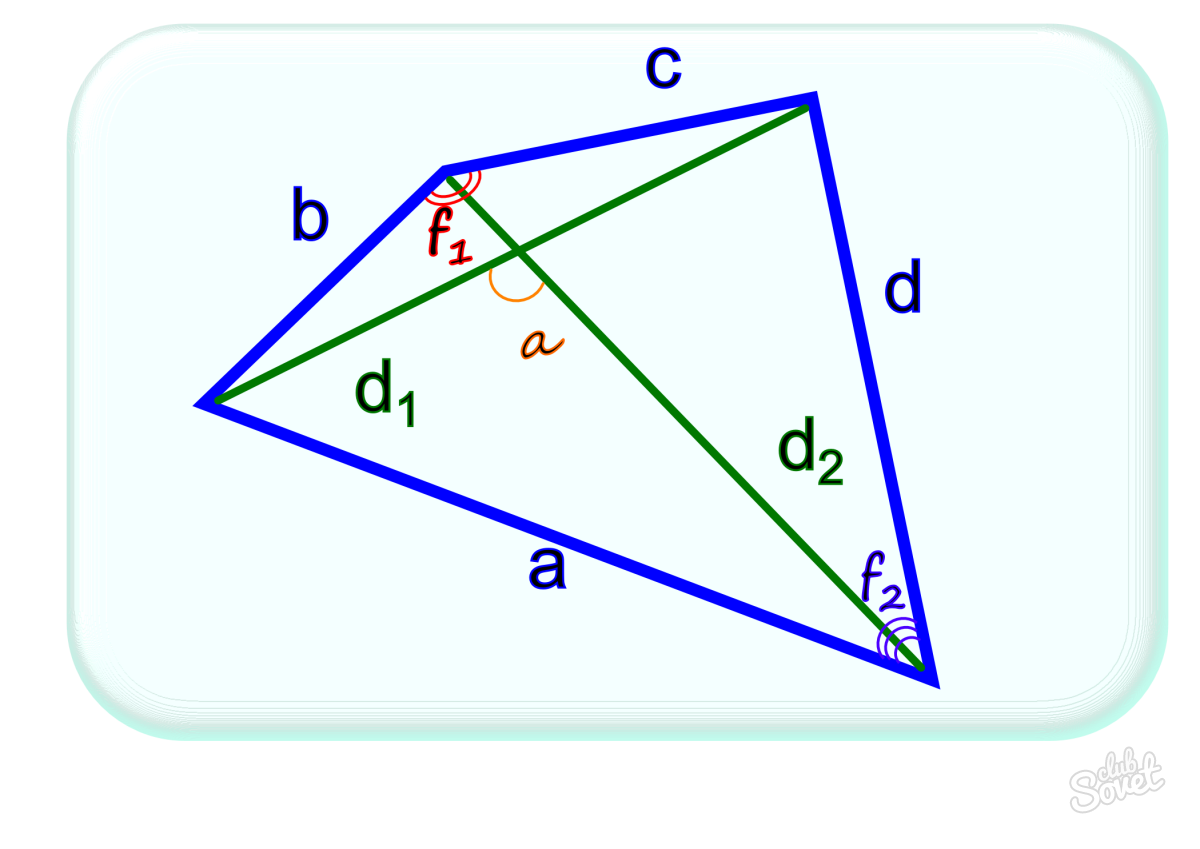
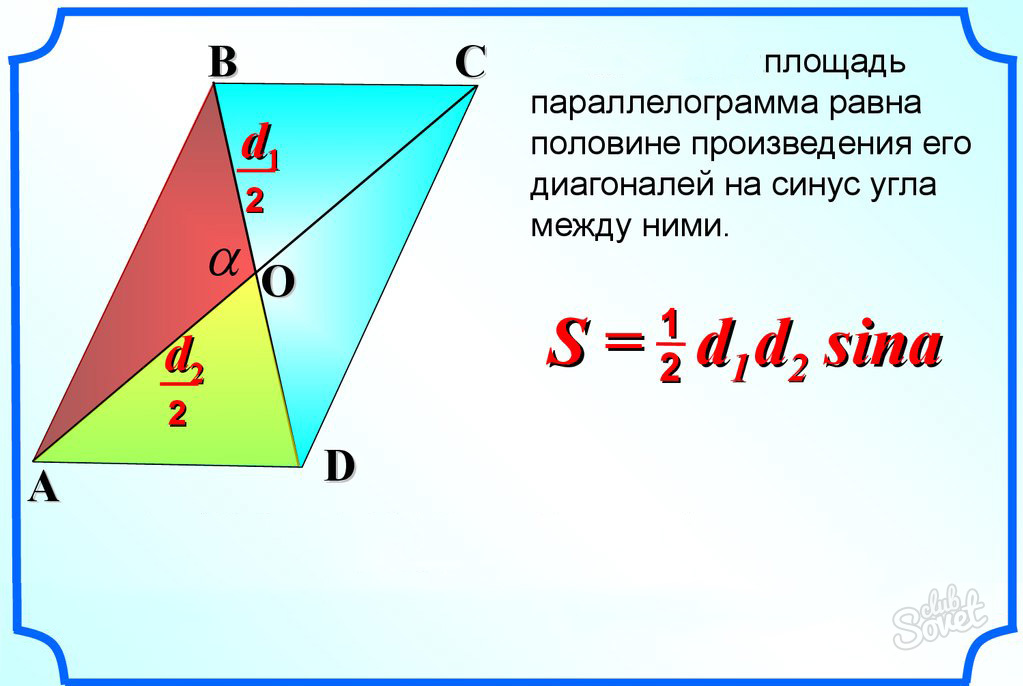
    Для нахождения его площади вам потребуются диагонали фигуры, а также угол, полученный как результат их пересечения.

    • S = (d1*d2*sinα)/2,
    • d1, d2 – диагонали,
    • α – угол, полученный путем их пересечения.

    Четуг

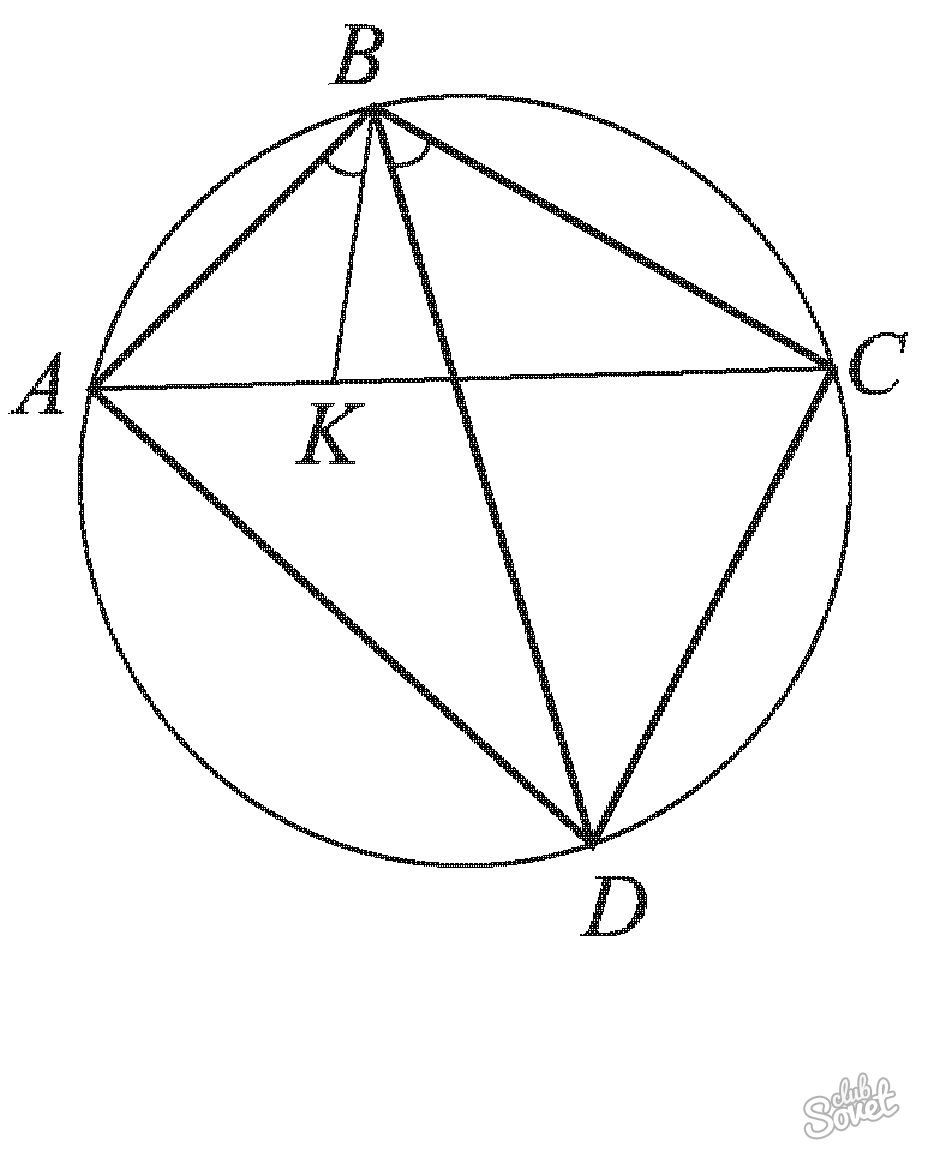
    Многоугольник в окружности

    Если заданный четырехугольник помещен в окружность, известна длина сторон фигуры, то в определении площади многоугольника поможет соотношение:

    S = √(p – m)(p – k)(p – l)(p – e), p = (m + k + l + e)/2.
    m, k, l, e – его стороны.

    2

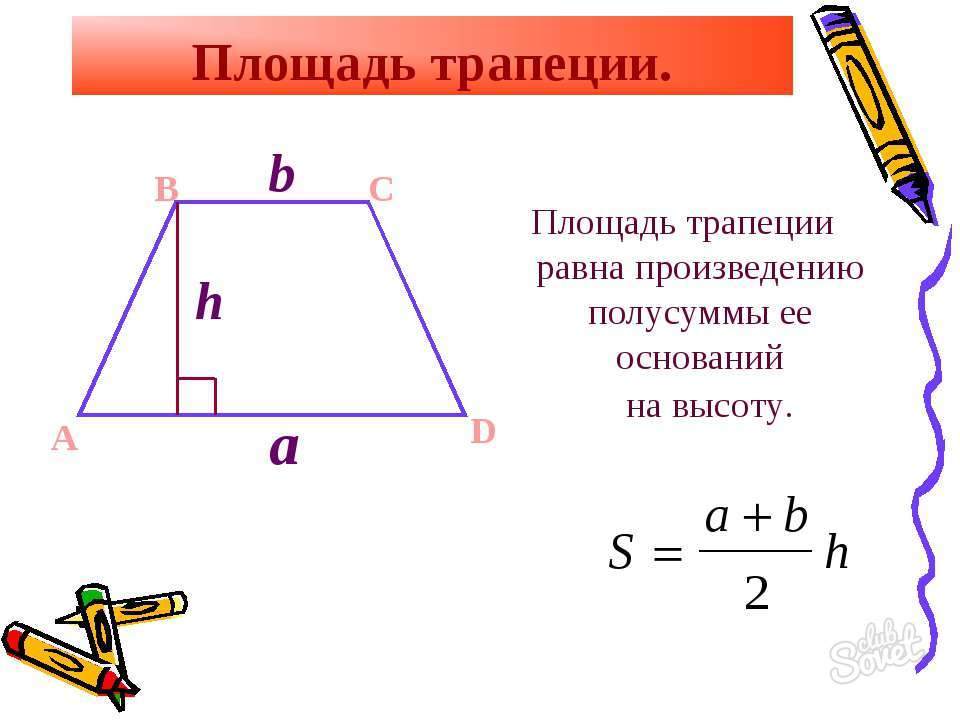
    Как найти площадь четырехугольника – трапеции

    Данную фигуру отличает наличие параллельных 2-ух сторон. Чтобы определить площадь такого многоугольника воспользуйтесь такими параметрами:

    • Если известны величины параллельных сторон и перпендикуляра-высоты, проведенной к ним, площадь вычисляется с помощью выражения S = ((a + b)*h)/2,
      a и b – основания,
      h – перпендикуляр-высота.
    • Исходя из определения линии средины (k = (a + b)/2)), предыдущая формула приобретет следующий вид: S = k*h,
      k – линия средины.
      Известные диагонали трапеции и градусная мера угла, образованная в результате их пересечения, также помогут определить площадь фигуры: S = (d1*d2*sinβ)/2,
      d1, d2 – диагонали,
      β – угол, полученный путем их пересечения.
    • Заданы 4 стороны: S = ((m + l)√k2 – ((m – l)2 + k2– d2)2/(4(m – l)2))/2,
      m, l – стороны параллельные,
      k, d – стороны боковые.

    3

    Как найти площадь четырехугольника – дельтоида

    Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:

    • Известны стороны фигуры и угол, образованный сторонами разной длины:
      S = m*l*sinϕ,
      m, l – стороны дельтоида,
      ϕ – угол между ними.
    • Известны стороны фигуры и углы, образованные сторонами равной длины:
      S = m2*sinα/2 + l2*sinβ/2,
      m, l – стороны дельтоида,
      α, β – углы между равными сторонами.
    • Наличие известных диагоналей также позволяет определить площадь фигуры:
      S = d1*d2/2,
      d1, d2 – диагонали дельтоида.
    • Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
      m, l – стороны дельтоида,
      r – радиус в случае вписанной окружности.

    4

    Как найти площадь четырехугольника – параллелограмма

    Если выпуклый многоугольник имеет 2 пары непересекающихся сторон, то перед вами – параллелограмм.

    Общее выражение

    Для определения площади данного вида фигуры потребуются:

    • Сторона четырехугольника и высота, на нее опущенная: S = k*h(k),
      k – сторона фигуры,
      h(k) – высота к ней.
    • Длина двух сторон, имеющих одну вершину, и градусная мера угла при данной вершине:
      S = l*k*sinϕ,
      k, l – стороны многоугольника,
      ϕ – угол между ними.
    • Диагонали фигуры и угол, полученный как результат их пересечения: S = d1*d2*sinβ/2,
      d1, d2 – диагонали,
      β – угол – результат их пересечения.

    Ромб

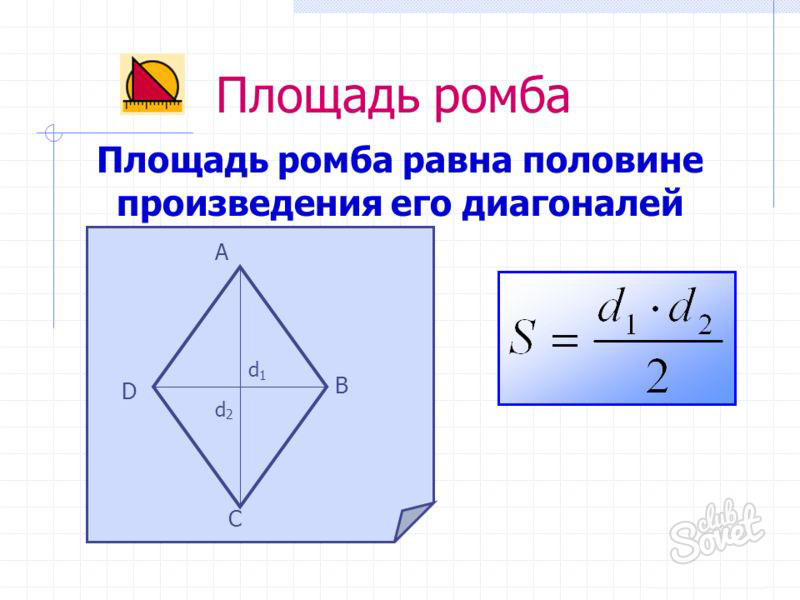
    Данный четырехугольник – частный случай параллелограмма, имеющий 4 равные стороны. Поэтому выражения, справедливые для параллелограмма, верны и для него. Тогда

    • S = k*h(k),
      k – сторона фигуры, h(k) – высота к ней.
    • S = k2*sinϕ,
      k – сторона четырехугольника, ϕ – угол между сторонами.
    • S = d1*d2/2 (т.к. диагонали фигуры при пересечении образую прямой угол, а sin90° = 1),
      d1, d2 – диагонали многоугольника.

    Прямоугольник

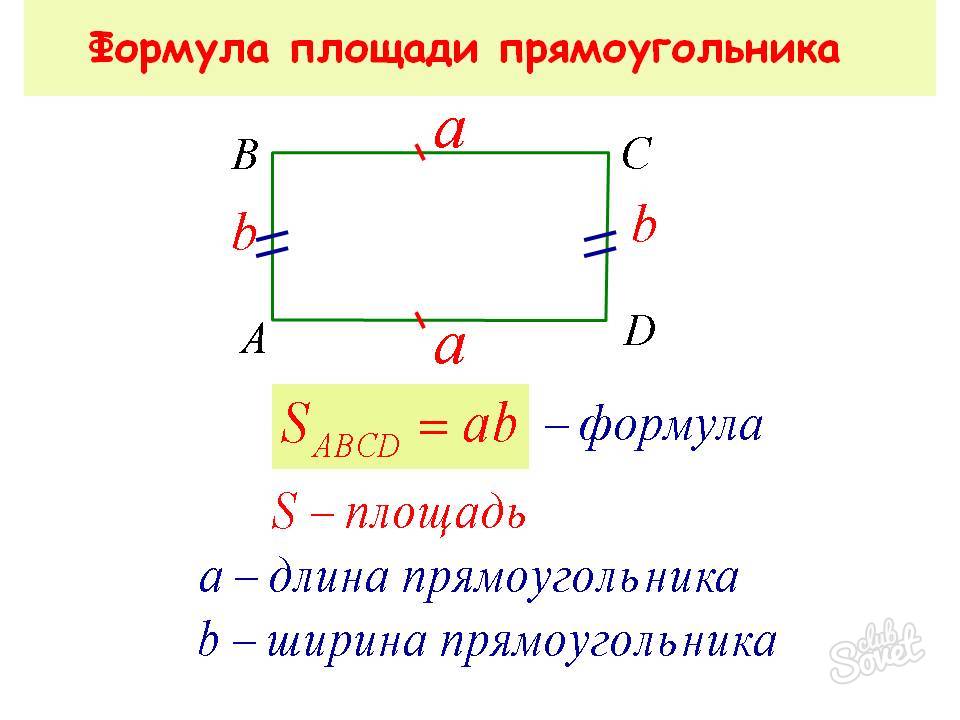
    Такой многоугольник имеет 2 пары равных сторон, а градусная мера его углов – 90°. Для нахождения его площади справедливы следующие выражения:

    • S = k*l,
      k, l – стороны фигуры.
    • S = d2*sinβ/2,
      d – диагонали четырехугольника, β – угол – результат их пересечения.
    • S = 2R2*sinβ,
      R – радиус в случае описанной окружности.

    Квадрат

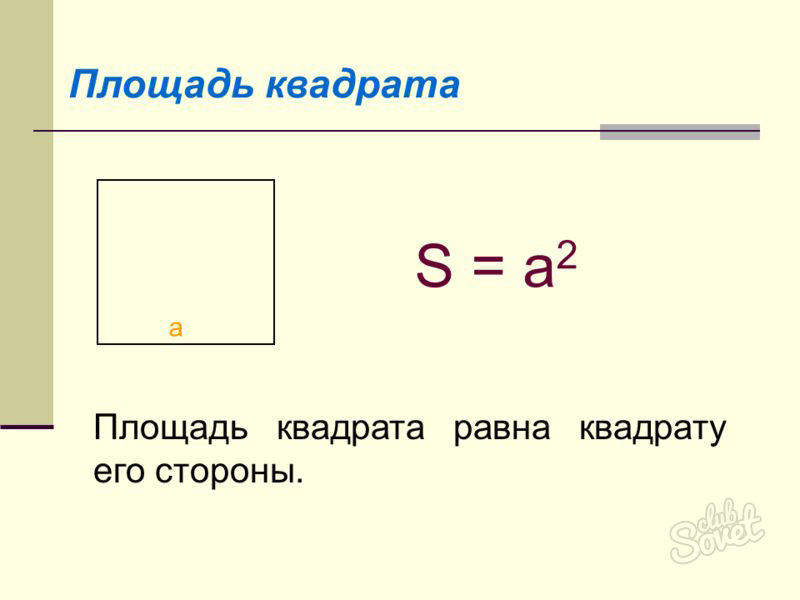
    В данном случае у соотношения, полученные на предыдущем этапе, приобретут следующий вид (т.к. стороны такого вида прямоугольника равны):

    • S = k2, k – сторона фигуры.
    • S = d2/2, d – диагональ квадрата.
    • S = 2R2, R – радиус в случае описанной окружности.
    • S = 4r4, r – радиус в случае вписанной окружности.

    Источник

    Определение.

    Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.

    Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?

    Теорема 1.

    В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.

    vpisannaya-v-chetyrekhugolnik-okruzhnostВ четырехугольник ABCD можно вписать окружность, если

    AB+CD=BC+AD.

    И обратно, если суммы противоположных сторон четырехугольника равны:

    AB+CD=BC+AD,

    то в четырехугольник ABCD можно вписать окружность.

    Теорема 2.

    Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.

    centr-vpisannoj-v-chetyrekhugolnik-okruzhnostiO — точка пересечения биссектрис четырехугольника ABCD.

    AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,

    то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.

    3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.

    tochki-kasaniya-vpisannoj-v-chetyrekhugolnik-okruzhnostiAM=AN,

    BM=BK,

    CK=CF,

    DF=DN

    (как отрезки касательных, проведенных из одной точки).

    4.

    radius-vpisannoj-v-chetyrekhugolnik-okruzhnosti

        [OM bot AB,]

        [OK bot BC,]

        [OF bot CD,]

        [ON bot AD]

    (как радиусы, проведенные в точки касания).

    5. Площадь четырехугольника связана с радиусом вписанной в него  окружности формулой

        [S = p cdot r,]

    где p — полупериметр четырехугольника.

    Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.

    Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и

        [{S_{ABCD}} = (AD + BC) cdot r,]

    или

        [{S_{ABCD}} = (AB + CD) cdot r.]

    Соответственно, радиус вписанной в четырехугольник окружности равен

        [r = frac{S}{p}]

    Для описанного четырехугольника ABCD

        [r = frac{{{S_{ABCD}}}}{{AD + BC}}]

    или

        [r = frac{{{S_{ABCD}}}}{{AB + CD}}.]

    Источник

    Как рассчитать площадь четырехугольника

    На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.

    Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.

    Через диагонали и угол между ними

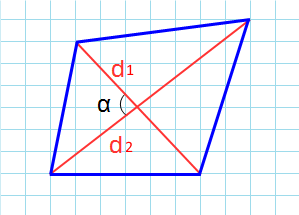
    Площадь четырехугольника через диагонали

    Формула для нахождения площади четырехугольников через диагонали и угол между ними:

    d1, d2 – диагонали; α – угол между диагоналями.

    Через стороны и противолежащие углы

    Площадь четырехугольника через стороны и противолежащие углы

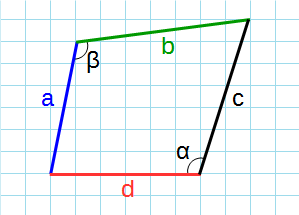
    Формула для нахождения площади четырехугольников через стороны и противолежащие углы:

    p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.

    Площадь вписанного четырехугольника в окружность

    Площадь вписанного четырехугольника в окружность

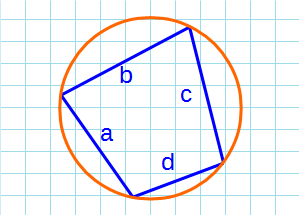
    Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:

    p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника.

    Площадь описанного четырехугольника около окружности через радиус

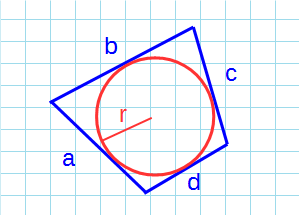
    Площадь описанного четырехугольника около окружности

    Формула для нахождения площади описанного четырехугольника около окружности через радиус:

    p – полупериметр четырехугольника; r – радиус вписанной окружности; a, b, c, d – стороны четырехугольника.

    Площадь описанного четырехугольника около окружности через стороны и противолежащие углы

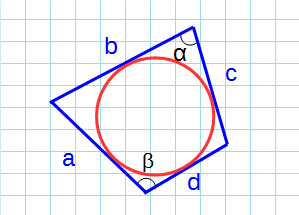
    Площадь описанного четырехугольника около окружности

    Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:

    p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.

    Источник

    Формулы площадей фигур

    формулы площадей фигур

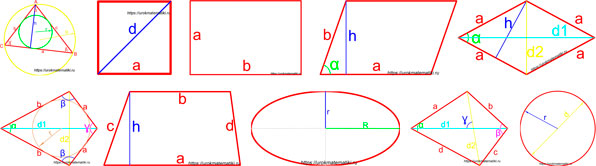
    Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

    • формулы площади треугольника
    • формулы площади квадрата
    • формула площади прямоугольника
    • формулы площади параллелограмма
    • формулы площади ромба
    • формулы площади трапеции
    • формулы площади дельтоида
    • формулы площади произвольного выпуклого четырехугольника
    • формулы площади круга
    • формула площади эллипса

    Формулы площади треугольника

    формулы площади треугольника

    Формула площади треугольника по стороне и высоте

    формула площади треугольника по стороне и высоте

    Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

    S = 12 a · h

    ,

    где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

    Формула площади треугольника по трем сторонам

    формула площади треугольника по трем сторонам

    Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.

    S = pp-ap-bp-c

    ,

    где p — полупериметр треугольника: p = a + b + c2
    a, b, c — стороны треугольника.

    Формула площади треугольника по двум сторонам и углу между ними

    формула площади треугольника по двум сторонам и углу между ними

    Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

    S = 12 a · b · sinγ

    ,

    где a, b — стороны треугольника,
    γ — угол между сторонами a и b.

    Формула площади треугольника по трем сторонам и радиусу описанной окружности

    формула площади треугольника по трем сторонам и радиусу описанной окружности

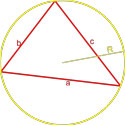
    S = a · b · c4R

    ,

    a, b, c — стороны треугольника,
    R – радиус описанной окружности.

    Формула площади треугольника по трем сторонам и радиусу вписанной окружности

    формула площади треугольника по трем сторонам и радиусу вписанной окружности

    Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

    S = p · r

    ,

    где S — площадь треугольника,
    r – радиус вписанной окружности,
    p — полупериметр треугольника: p = a + b + c2

    Формулы площади квадрата

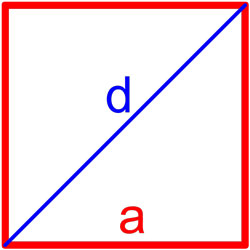
    формулы площади квадрата

    Формула площади квадрата по длине стороны

    формула площади квадрата по длине стороны

    Площадь квадрата равна квадрату длины его стороны.

    S = a2

    ,

    где S — площадь квадрата,
    a — длина стороны квадрата.

    Формула площади квадрата по длине диагонали

    формула площади квадрата по длине диагонали

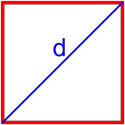
    Площадь квадрата равна половине квадрата длины его диагонали.

    S = d22

    ,

    где S — площадь квадрата,
    d — длина диагонали квадрата.

    Формула площади прямоугольника

    формула площади прямоугольника

    Площадь прямоугольника равна произведению длин двух его смежных сторон.

    S = a · b

    ,

    где S — площадь прямоугольника,
    a, b — длины сторон прямоугольника.

    Формулы площади параллелограмма

    Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

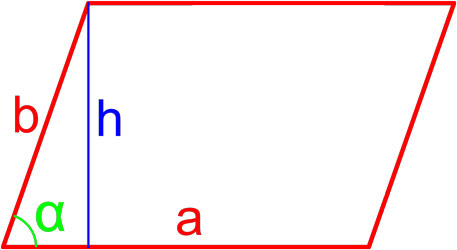
    формулы площади параллелограмма

    Формула площади параллелограмма по длине стороны и высоте

    формула площади параллелограмма по длине стороны и высоте

    Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

    S = a · h

    ,

    где S — площадь параллелограмма,
    a, h — длины сторон параллелограмма.

    Формула площади параллелограмма по двум сторонам и углу между ними

    формула площади параллелограмма по двум сторонам и углу между ними

    Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

    S = a · b · sinα

    ,

    где S — площадь параллелограмма,
    a, b — длины сторон параллелограмма,
    α – угол между сторонами параллелограмма.

    Формула площади параллелограмма по двум диагоналям и углу между ними

    формула площади параллелограмма по двум диагоналям и углу между ними

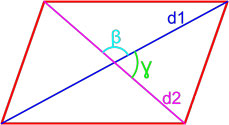
    Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

    S =
    d1 · d2
    · sinβ2 = d1 · d2
    · sinγ2

    ,

    где S — площадь параллелограмма,
    d1, d2 — длины диагоналей параллелограмма,
    β, γ – угол между диагоналями параллелограмма.

    Формулы площади ромба

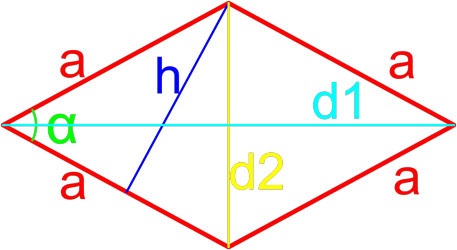
    формулы площади ромба

    Формула площади ромба по длине стороны и высоте

    формула площади ромба по длине стороны и высоте

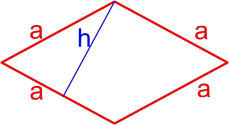
    Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

    S = a · h

    ,

    где S — площадь ромба,
    a — длина стороны ромба,
    h — длина высоты ромба.

    Формула площади ромба по длине стороны и углу

    формула площади ромба по длине стороны и углу

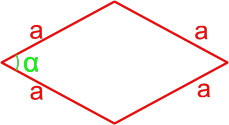
    Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

    S = a2 · sinα

    ,

    где S — площадь ромба,
    a — длина стороны ромба,
    α — угол между сторонами ромба.

    Формула площади ромба по длинам его диагоналей

    формула площади ромба по длинам его диагоналей

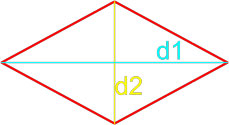
    Площадь ромба равна половине произведению длин его диагоналей.

    S = d1 · d22

    ,

    где S — площадь ромба,
    d1, d2 — длины диагоналей ромба.

    Формулы площади трапеции

    Трапеция — это четырёхугольник, у которого две (a, b) стороны параллельны (основания), а две другие (c, d) стороны не параллельны (боковые стороны).

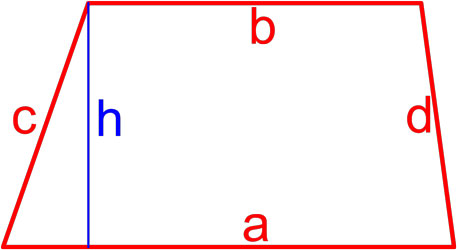
    формулы площади трапеции

    Формула Герона для трапеции

    формула Герона для трапеции

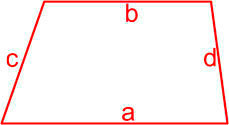
    S = a + b|a – b| p-ap-bp-a-cp-a-d

    ,

    где S — площадь трапеции,
    a, b — длины основ трапеции,
    c, d — длины боковых сторон трапеции,
    p=a+b+c+d2 — полупериметр трапеции.

    Формула площади трапеции по длине основ и высоте

    формула площади трапеции по длине основ и высоте

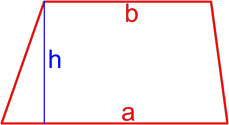
    Площадь трапеции равна произведению полусуммы её оснований на высоту.

    S = a + b · h2

    ,

    где S — площадь трапеции,
    a, b — длины основ трапеции,
    h — высота трапеции.

    Формулы площади дельтоида

    Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

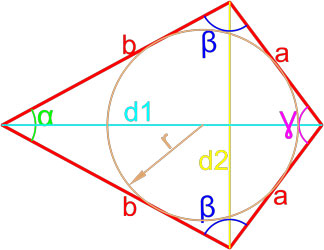
    формулы площади дельтоида

    Формула площади дельтоида по двум неравным сторонам и углу между ними

    формула площади дельтоида по двум неравным сторонам и углу между ними

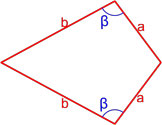
    Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

    S = a·b sinβ

    ,

    где S — площадь дельтоида,
    a, b — длины неравных сторон дельтоида,
    β — угол между неравными сторонами дельтоида.

    Формула площади дельтоида по равным сторонам и углу между ними

    формула площади дельтоида по равным сторонам и углу между ними

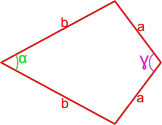
    Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

    S = a2 sinγ + b2 sinα2

    ,

    где S — площадь дельтоида,
    a, b — длины сторон дельтоида,
    α — угол между равными сторонами b,
    γ — угол между равными сторонами a.

    Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

    формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

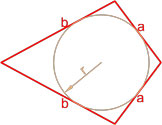
    Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

    S = a+b r

    ,

    где S — площадь дельтоида,
    a, b — длины неравных сторон дельтоида,
    r — радиус вписанной окружности.

    Формула площади дельтоида по двум диагоналям

    формула площади дельтоида по двум диагоналям

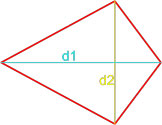
    Площадь дельтоида равна половине произведения длин двух диагоналей.

    S = d1 · d22

    ,

    где S — площадь дельтоида,
    d1, d2 — диагонали дельтоида.

    Формулы площади произвольного выпуклого четырехугольника

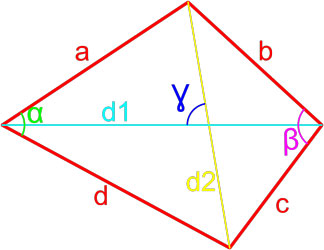
    формулы площади выпуклого четырехугольника

    Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

    формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

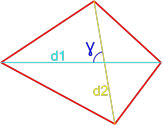
    Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.

    S = d1 · d2 · sinγ2

    ,

    где S — площадь четырехугольника,
    d1, d2 — диагонали четырехугольника,
    γ — любой из четырёх углов между диагоналями.

    Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

    формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

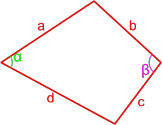
    S = p-ap-bp-cp-d – a·b·c·d ·cos2θ

    ,

    где S — площадь четырехугольника,
    a, b, c, d — длины сторон четырехугольника,
    p=a+b+c+d2 — полупериметр четырехугольника,
    θ = α + β2 — полусумма двух противоположных углов четырехугольника.

    Формула площади вписанного четырехугольника (формула Брахмагупты)

    формула площади вписанного четырехугольника (формула Брахмагупты)

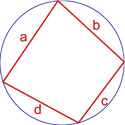
    Если вокруг четырехугольника можно описать окружность, то его площадь равна

    S = p-ap-bp-cp-d

    ,

    где S — площадь четырехугольника,
    a, b, c, d — длины сторон четырехугольника,
    p=a+b+c+d2 — полупериметр четырехугольника.

    Формула площади четырехугольника с вписанной окружностью

    формула площади четырехугольника с вписанной окружностью

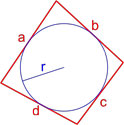
    Если в четырехугольник можно вписать окружность, то его площадь равна:

    S = p· r

    ,

    где S — площадь четырехугольника,
    r — радиус вписанной окружности,
    p=a+b+c+d2 — полупериметр четырехугольника.

    Формула площади четырехугольника с вписанной и описанной окружностями

    формула площади четырехугольника с вписанной и описанной окружностями

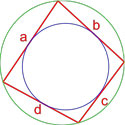
    Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:

    S = a·b·c·d

    ,

    где S — площадь четырехугольника,
    a, b, c, d — длины сторон четырехугольника.

    Формулы площади круга

    формулы площади круга

    Формула площади круга через радиус

    Площадь круга равна произведению квадрата радиуса на число пи.

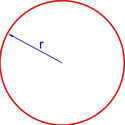
    формула площади круга через радиус

    S = πr2

    ,

    где S — площадь круга,
    r — радиус круга.

    Формула площади круга через диаметр

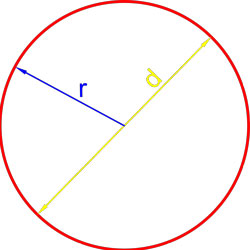
    формула площади круга через диаметр

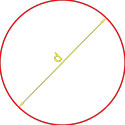
    Площадь круга равна четверти произведения квадрата диаметра на число пи.

    S = πd24

    ,

    где S — площадь круга,
    d — диаметр круга.

    Площадь сегмента круга

    площадь сегмента круга

    Площадь кругового сегмента через угол в градусах.

    S = R22 · π · α°180° – sinα

    ,

    где S — площадь сегмента круга,
    R — радиус круга,
    α° — угол в градусах.

    Площадь кругового сегмента через угол в радианах.

    S = R22 · αрад. – sinα

    ,

    где S — площадь сегмента круга,
    R — радиус круга,
    α° — угол в радианах.

    Формула площади эллипса

    формула площади эллипса

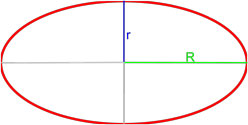
    Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

    S = π · a · b

    ,

    где S — площадь эллипса,
    a — длина большей полуоси эллипса,
    b — длина меньшей полуоси эллипса.

    • Коротко о важном
    • Таблицы
    • Формулы
    • Формулы по геометрии
    • Теория по математике
    Источник

    Добавить комментарий