Вариация функционала
Для
дифференцируемой функции (2.18) дифференциал
dy
– это главная, линейная относительно
dx,
часть приращения функции: 1-е слагаемое
формулы (2.18):
-

(2.27)
Для
варьируемого функционала аналогом
дифференциала функции будет вариация.
Определение
21. Вариацией
dJ(y)
функционала J(y)
на функции y(x)
называется главная, линейная относительно
dy,
часть его приращения на этой функции
ΔJ.
Согласно
(2.25) вариация будет линейным относительно
dy
функционалом. Конечно, вариация будет
также зависеть и от той функции y(x),
на которой она вычисляется. Применяя
вывод 1′, мы можем сказать:
Вывод
7. Если
![]() dJ(y)
dJ(y)
в Ck,
то она существует и в Ck+1.
Как
же вычислить вариацию функционала?
Здесь возможны различные способы. Мы
рассмотрим 2 способа, которые будем
применять дальше при исследовании
функционалов на экстремум.
1
способ вычисления вариации функционала.
Даём бесконечно малое приращение dy
функции y(x)
– аргументу нашего функционала. Вычисляем
приращение ΔJ,
вызванное этой вариацией. Раскладываем
его в ряд Тейлора с удержанием только
линейных членов.
Этот
способ мы будем использовать в следующих
главах при выводе дифференциальных
уравнений Эйлера. А сейчас рассмотрим
2-й способ, который нам пригодится при
выводе необходимого условия экстремума.
2
способ вычисления вариации функционала.
Пусть y0(x)
– та функция, на которой нам нужно
вычислить вариацию функционала dJ.
Рассмотрим класс функций вида
-

(2.28)
где
a – бесконечно малая величина, а h(x)
– фиксированная функция. Этот класс
является более узким, чем исходный
класс функций: в нём все ординаты
меняются пропорционально одному
числовому параметру a. На рис.2.7 показана
исходная функция y0(x),
несколько функций из класса (2.28) и
функция, не принадлежащая классу (2.28).
|
|
|
Рис. |
Мы
знаем, что, если существует dJ
на каком-либо классе функций, то она
существует и на более узком классе.
Поэтому по способу 2 мы будем вычислять
вариацию функционала на классе функций
(2.28). Так как в функциях (2.28) y0(x)
и h(x)
– фиксированные, то функционал на
функциях вида (2.28) становится фактически
функцией одной переменной a:
-

(2.29)
причём
V(0)
соответствует функционалу на исходной
функции y0(x).
Найдём приращение функционала:
-
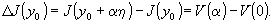
(2.30)
Так
как функционал – варьируемый, то по
(2.25) имеем:
-

(2.31)
или,
с учётом линейности (2.23):
-

(2.32)
Нам
нужно выделить в этом выражении линейный
функционал L(y0,h),
это и будет интересующая нас вариация
функционала. Для этого разделим обе
части (2.32) на a и перейдём к пределу при
a→0. В правой части 1-е слагаемое даст
интересующую нас величину L(y0,h).
Второе слагаемое стремится к нулю.
Действительно, первый множитель |a|/a
ограничен по модулю, третий множитель
||h|| – это норма фиксированной функции
– также постоянная величина, а вот второй
множитель b – это бесконечно малая
величина, она стремится к нулю при a→0.
Следовательно, предел правой части –
это вариация функционала dJ.
Найдём предел левой части. В силу (2.30):
-

(2.33)
Таким
образом, вычисление вариации функционала
по 2-му правилу сводится к вычислению
производной по a от J(y0+ah)
при a=0:
-

(2.34)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вариационное исчисление и Вариационные алгоритмы
Время на прочтение
5 мин
Количество просмотров 7.3K

В этой статье будут рассмотрены основные задачи в вариационном исчислении. Также применение вариационных алгоритмов в машинном обучении. Поэтому, если вы готовы погрузится в одну из очень интересных тем математики и вы любитель машинного обучения, продолжайте читать.
В конце статьи будет объяснение теории вероятностных глубоких нейросетей, в котором применяется . вариационный вывод
Вариационное исчисление –это область математического анализа, которая использует вариации, представляющие собой небольшие изменения функций и функционалов, для нахождения максимумов и минимумов функционалов: отображений из набора функций в действительные числа. Функционалы часто выражаются как определенные интегралы, включающие функции и их производные.
Это определение из википедии можно переформулировать так – мы изучаем изменения функций или функционалов, ищем экстремумы… Не одной ли мне кажется, что эта часть мат анализа имеет достаточные сходства с математикой таких моделей, как нейронные сети. После рассмотрения теории Вариационного исчисления будет описание ответа на этот вопрос (спойлер я думаю, вы уже знаете)
Примеры задач вариационного исчисления
Предлагаю рассмотреть/повторить пару основных уравнений и понятий. Я буду писать математические определения, и описывать их более простым языком.
Одним из самых важных определений в этой области является функционал. Пусть существует множество функций, удовлетворяющих некоторым условиям. Закон или правило, по которому каждой функции из данного множества ставится в соответствие вполне определенное числовое значение, называется функционалом, определенным на данном множестве функций
Если дана функция
то через
обозначается приращение независимой переменной x.
А если взять множество функций и рассматривать их, как интегралы, то получится функционал
А в функционале I[y(x)] приращение аргумента y(x) называется вариацией функции y(x) и обозначается через
Чем ближе кривая y_1(x) к кривой y(x) , тем меньше δy
Такое понятие, как приращение функционала I[y(x)] дается в виде
Вариация функционала — обобщение понятия дифференциала функции одной переменной, главная линейная часть приращения функционала вдоль определенного направления. Понятие используется в теории экстремальных задач для получения необходимых и достаточных условий экстремума. Именно такой смысл вкладывается в этот термин, начиная с работы 1762 года Ж. Лагранжа
Экстремумы
Напоминаю, что нахождение экстремумов функции (минимумов или максимумов) сводится к поиску точки, в которых производная функции является нулю. Экстремумы функционалов можно получить, найдя функции, у которых функциональная производная равна нулю. Что приводит к решению уравнения Эйлера – Лагранжа
Если значения функционала I[y(x)] на всех кривых, достаточно близких к кривой y = y_0(x) , меньше, чем I[y_0(x)] , то говорят, что функционал I[y(x)] достигает своего максимума на кривой y = y_0(x)
Под функционалом нужно понимать интеграл. Другими словами, кривая y_0(x) является максимумом для функционала I[y(x)] если все остальные значения функционала меньше, чем значение функционала от этой кривой(y_0(x)).
В этом случае имеет место неравенство
Если только на такой кривой, приращение функционала является нулём, то говорят, что на этой кривой функционал достигает абсолютного максимума.
Такая же история и с минимумом, кривая y_0(x) является минимумом для функционала I[y(x)], если все остальные значения функционала больше, чем значение функционала от этой кривой(y_0(x)).
Мы просмотрели основные понятия, при работе с распределениями функций.
Вариационный алгоритм в модели машинного обучения
Когда я говорила о сходстве вариационных задач и теории нейронных сетей, я не имела ввиду, что дифференциальное исчисление каким то образом похоже на вариационное. Ведь в вариационном исчислении ищутся функции, доставляющие экстремум функционалам. Предположение заключается в сходстве задач, а не реализации.
Оказывается, вариационные алгоритмы применяются в некоторых нейро-сетевых моделях, где аналитическое решение неразрешимо.
В нейронных алгоритмах, (и не только), мы всегда ищем точку в пространстве параметров, в которых функция потерь имеет минимальное значение. Вариационное исчисление появляется в момент, когда мы преобразуем функцию потерь в другую функцию потерь,(зачастую это нижняя вариационная граница), используя методы вариационного исчисления.
Вариационные методы-это семейство методов аппроксимации трудноразрешимых интегралов, возникающих при байесовском выводе .
Например, в Вариационных автоэнкодерах, Expectation–maximization algorithm или в реализации байесовской статистики в нейросети “Bayes by Backprop”
Для того, чтобы всё было понятно, давайте возьмём пример – “Bayes by Backprop” в вероятностных нейросетях.
Вариационный вывод в алгоритме “Bayes by Backrop”

Вообще, эта архитектура нейросети очень интересна, ниже будет объяснение основных концептов и, конечно, вариационной части
Здесь нужно быть знакомым с основами вероятности и Байесовской статистикой.
Во-первых, нужно понять, что мы представляем веса, как дисперсию и среднее значение в распределении.
Здесь мы определяем аппроксимированное распределение, которое мы хотим оптимизировать, чтобы оно было максимально похоже на неизвестное истинное распределение.
В теории таких алгоритмов, под θ нужно понимать веса модели, а под D данные
В математике уже определенно уравнение для оценки расхождения между двумя распределениями – KL – divergence

естественно, нам нужно бы определить это за функцию потери и минимизировать её но…

Мы сталкиваемся с проблемой неразрешимого интеграла.
Вот на этом шагу и начинаются вычисления с Вариационным выводом…
Решением проблемы является применение максимизации следующей функции:

ВЫВОД этого решения я рекомендую Вам прочесть, ( потому как это и есть тема статьи)
Вариационные исчисления, применяемые для этой функции
Если присмотреться к KL – расхождению, можно заметить что это очень похоже на мат ожидание! (E)

Если мы переместимся к нашей оптимизационной функции и выполним немного вычислений, то получим такую разность:

В этой статье ОБЯЗАТЕЛЬНО стоит ввести термин нижней вариационной границы(Variational Lower Bound) (ELBO).
Представим, что у нас есть функция
Нижняя граница на эту функцию будет любая функция,
удовлетворяющая уравнению:
вот пример нижней границы
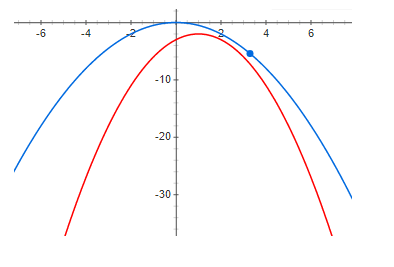
Думаю, почти все догадываются, где последней формуле стоит нижняя граница

*Обращаем внимание на минус*
Таким образом, максимизируя ELBO, мы оптимизируем модель!

Я считаю, что более углублённое описание концептов вариационного исчисление также требует отдельной статьи. Поэтому, возможно, где-то здесь в будущем появится ссылка на 2 часть этого всего).
Использованная литература
Вариационное исчисление: примеры и задачи
Вариационное исчисление для чайников
Древнейшей из задач на максимум и минимум является задача отыскания среди плоских замкнутных кривых заданной длины такую, которая охватывает наибольшую площадь (5 в до н.э.) – и это классическая изопериметрическая задача вариационного исчисления. Началось же классическое вариационное исчисление с задачи о кривой наискорейшего спуска (брахистохроне) в 1696 г. с публикации Иоганна Бернулли.
Общие принципы и методы решения задач вариационного исчисления были введены в 18 веке Эйлером и Лангранжем, они же установили тесную связь между ВИ и естествознанием. Далее на протяжении более чем двух столетий они разрабатывались, были найдены помимо необходимых условий первого порядка (уравнений Эйлера-Лагранжа) необходимые и достаточные услвоия второго порядка для сильных и слабых экстремумов.
На этой странице мы рассмотрим примеры с подробным решением следующих типов: простейшая задача вариационного исчисления, задача Больца, изопериметрическая задача, задача со старшими производными. А также научимся находить вариацию и допустимые экстремали функционала. Все это относится к классическому вариационному исчислению.
Смежные задачи вы можете найти в соответствующих разделах: Нелинейное программирование, Многокритериальная оптимизация, Математическое программирование и т.д.
Полезная страница? Сохрани или расскажи друзьям
Вариационное исчисление: задачи с решениями
Задача 1. Решить классическую задачу вариационного исчисления:
$$
int_0^1 dot{x}^2 dt to extr, quad x(0)=1, x(1)=0.
$$
Задача 2. Решить задачу Больца
$$
int_0^1 dot{x}^2 dt +alpha x^2(1) to extr, quad x(0)=1.
$$
Задача 3. Решить изопериметрическую задачу
$$
int_0^1 dot{x}^2 dt to extr, int_0^1 x^2 dt =3, quad x(0)=1, x(1)=6.
$$
Задача 4. Решить задачу со старшими производными
$$
int_0^pi (ddot{x}^2+4x^2) dt to extr, quad x(0) = dot x(0)=0, , dot x(pi)=sh(pi).
$$
Задача 5. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям
$$
J(y)=int_0^1 (e^y +xy’)dx, quad y(0)=0, y(1)=1.
$$
Задача 6. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям
$$
J(y)=int_0^1 e^{-x}cdot y” ^2 dx, quad y(0)=0, y'(0)=1, y(1)=e, y'(1)=2e.
$$
Задача 7. Для указанной вариационной задачи записать уравнение Эйлера и найти экстремаль, удовлетворяющую условиям $y(0) = 19, y(1)=30$
$$int_0^1 (1+y’^2)dx.$$
Задача 8. Найти вариацию функционала
$$int_0^1 (x+y’)ln sin y’ dx.$$
Задача 9. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям
$$
J(y)=int_0^{pi/4} (4ysin x +y’^2-y^2)dx, quad y(0)=0, y(pi/4)=0.
$$
Консультации и помощь
Нужно выполнить контрольную работу или задачи по вариационному исчислению и смежным предметам? Нет проблем! Стоимость консультации по решению – от 150 рублей, подробное оформление согласно требованиям методички в Word.
Решение задач вариационного исчисления на заказ
Полезные ссылки
- Вариационное исчисление: задачи, алгоритмы, примеры Крайне удобная для решения задач методичка: для каждого типа задач есть теория, краткий алгоритм и пример решения нескольких задач. Рекомендуем.
- Вариационное исчисление и основы теории управления Краткое учебное пособие с примерами задач по ВИ
- Эльсгольц Л.Э. Вариационное исчисление Классический учебник, теория изложена на простом уровне, множество разобранных примеров по каждому разделу.
- Изопериметрическая задача: теория и примеры решения

