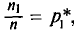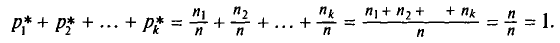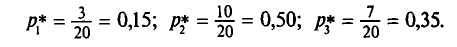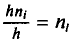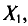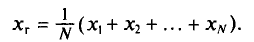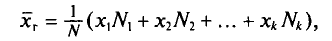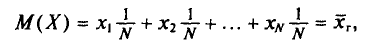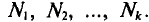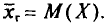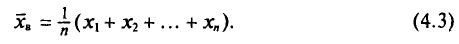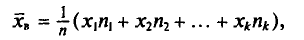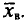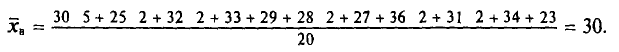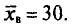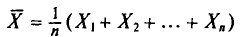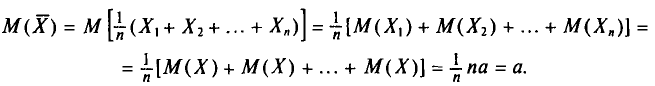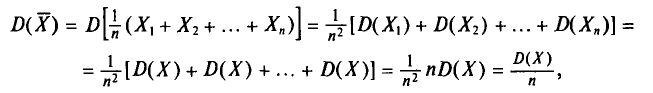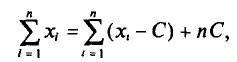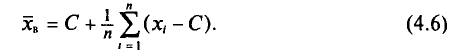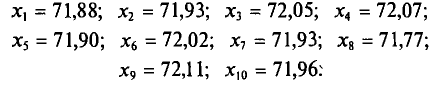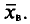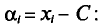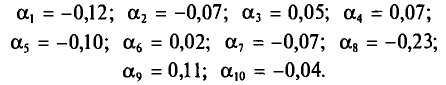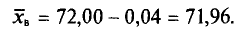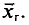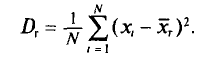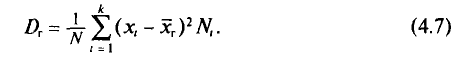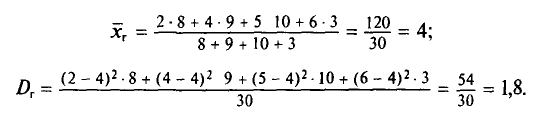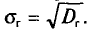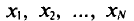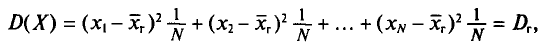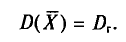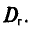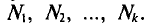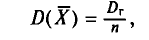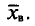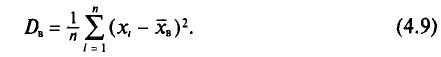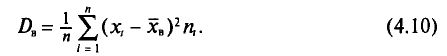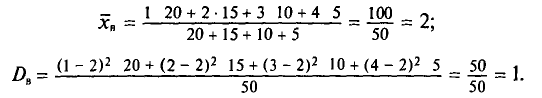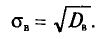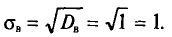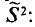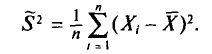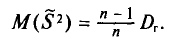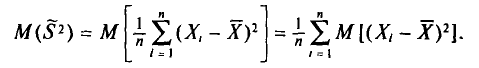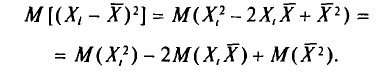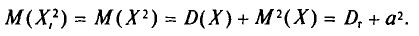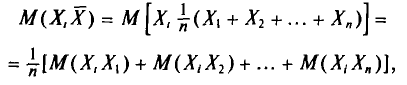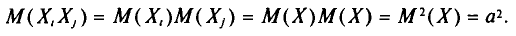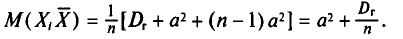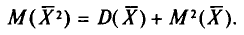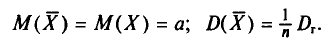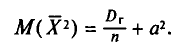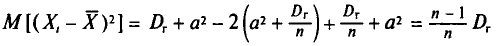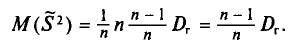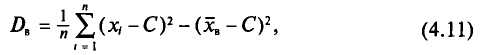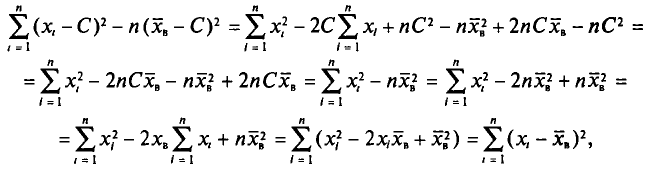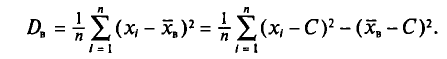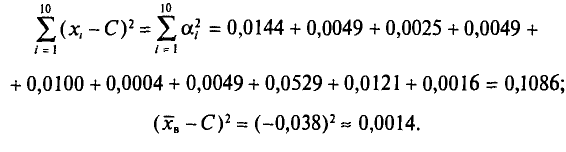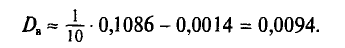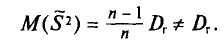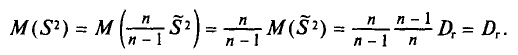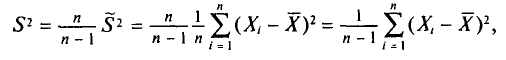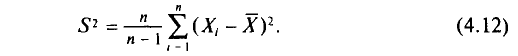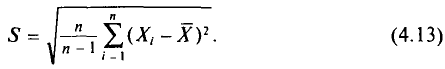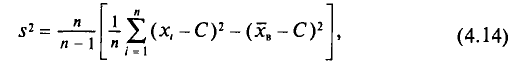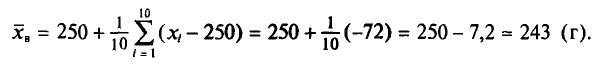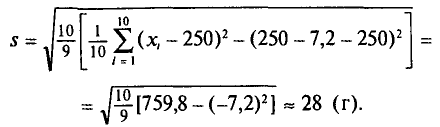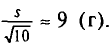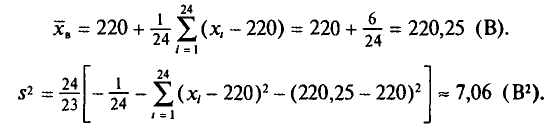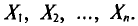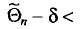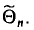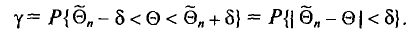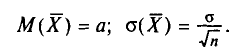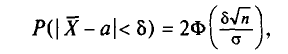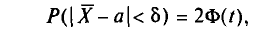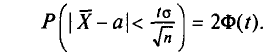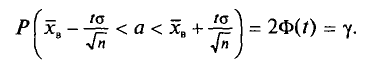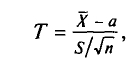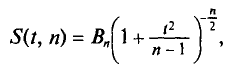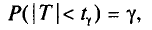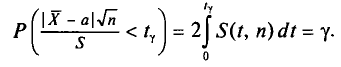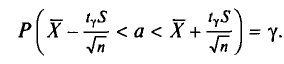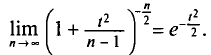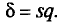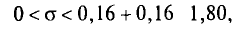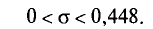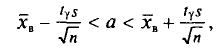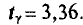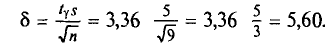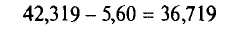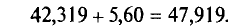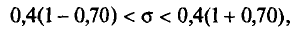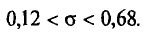Приступим к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки.
Пусть требуется изучить множество однородных объектов (это множество называют статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить соответствие детали стандартам, а количественным — контролируемый размер детали.
Лучше всего осуществить сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным причинам это сделать невозможно. Препятствовать сплошному обследованию может большое число объектов, их недоступность и т. п. Если, например, нужно знать среднюю глубину воронки при взрыве снаряда из опытной партии, то, проводя сплошное обследование, мы должны будем уничтожить всю партию.
Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.
Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки.
Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 —объем генеральной совокупности, а 10 —объем выборки.
Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной выборками незначительна
Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или, как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор осуществляется случайно. Например, для того чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики (массу, качество и пр.). Если вся выборка будет взята с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.
Статистическое распределение выборки. Полигон. Гистограмма
Пусть из генеральной совокупности извлечена выборка, причем 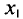
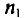
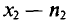
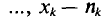
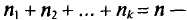
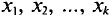
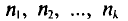
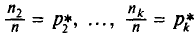
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.
Пример:
Перейдем от частот к относительным частотам в следующем распределении выборки объема n = 20:
Найдем относительные частоты:
Поэтому получаем следующее распределение:
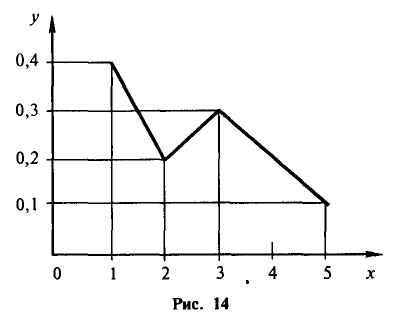
Для графического изображения статистического распределения используются полигоны и гистограммы.
Для построения полигона в декартовых координатах на оси Ох откладывают значения вариант 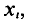
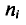
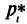
Пример:
Рис. 14 представляет собой полигон следующего распределения:
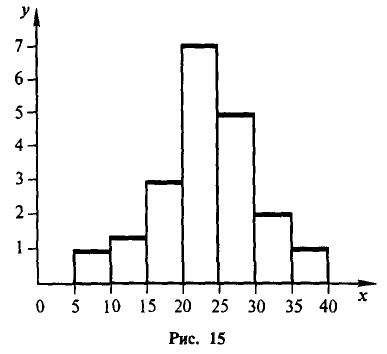
Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов шириной h и находят для каждого частичного интервала 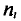
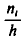
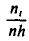
(или 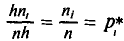
Пример:
Рис. 15 показывает гистограмму непрерывного распределения объема n =100, заданного следующей таблицей:
Оценки параметров генеральной совокупности по ее выборке
Выборка как набор случайных величин
Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится известным значение х признака X этого объекта. Таким образом, мы можем рассматривать извлечение объекта из генеральной совокупности как испытание, X—как случайную величину, а х —как одно из возможных значений X.
Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного определения) параметров, которыми описывается это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.
Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например значения количественного признака 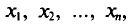
Опытные значения признака X можно рассматривать и как значения разных случайных величин 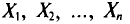
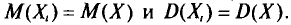
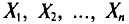
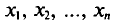
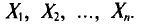
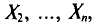
Генеральная и выборочная средние. Методы их расчета
Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X.
Определение:
Генеральной средней 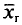
Если все значения 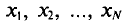
Если же значения признака 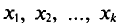
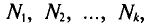

или
Как уже отмечалось (п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X.
Пусть все значения 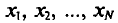
т. е.
Такой же итог следует, если значения 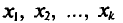
В случае непрерывного распределения признака X по определению полагают
Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n.
Определение:
Выборочной средней 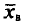
Если все значения 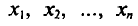
Если же значения признака 
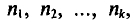

или
Пример:
Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28^27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю
Согласно формуле (4.4), имеем:
Итак,
Далее, не уменьшая общности рассуждений, будем считать значения 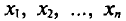
Разумеется, выборочная средняя для различных выборок того же объема n из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение і-го по счету объекта есть наблюдение случайной величины 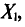
есть тоже случайная величина.
Таким образом, всевозможные получающиеся выборочные средние есть возможные значения случайной величины 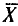
Найдем 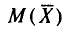
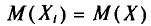
С учетом свойств математического ожидания (см. гл. II) получаем:
Итак, 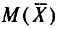
Теперь найдем 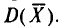
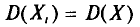
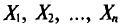
T. e.
Наконец, отметим, что если варианты 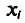
Так как
то формулу (4.3) можно преобразовать к виду
За константу С (так называемый ложный нуль) берут некоторое среднее значение между наименьшим и наибольшим значениями х, (і- 1, 2, …, n).
Пример:
Имеется выборка:
Требуется найти
Возьмем С =72,00 и вычислим разности
Их сумма: 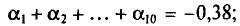
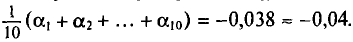
Генеральная и выборочная дисперсии
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.
Определение:
Генеральной дисперсией D, называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней
Если все значения 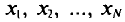
Если же значения признака 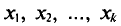
частоты 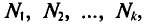

Пример:
Генеральная совокупность задана таблицей распределения:
Найдем генеральную дисперсию.
Согласно формулам (4.1) и (4.7), имеем:
Генеральным средним квадратическим отклонением (стандартом) называется
Пусть все значения 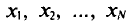
Найдем дисперсию признака X, рассматриваемого как случайная величина:
Так как 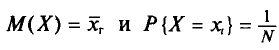
т. е.
Таким образом, дисперсия D(X) равна
Такой же итог можно получить, если значения 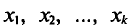
В случае непрерывного распределения признака X по определению полагают
С учетом формулы (4.8) формула (4.5) (п. 2) перепишется в виде
откуда 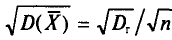
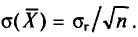
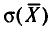
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 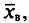
Определение:
Выборочной дисперсией 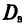
Если все значения 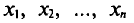
Если же значения признака 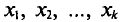
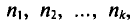
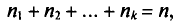
Пример:
Пусть выборочная совокупность задана таблицей распределения:
Найдем выборочную дисперсию. Согласно формулам (4.4) и (4.10), имеем:
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии:
В условиях примера 2 получаем, что
Далее, не уменьшая общности рассуждений, будем считать значения 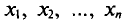
Выборочную дисперсию, рассматриваемую нами как случайная величина, будем обозначать
Теорема:
Математическое ожидание выборочной дисперсии равно 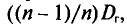
Доказательство:
С учетом свойств математического ожидания (см. гл. II) получаем
Вычислим одно слагаемое 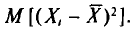
Вычислим по отдельности эти математические ожидания.
Согласно свойству I дисперсии (см. гл. И) и формулам (4.2), (4.8) имеем
Далее, с учетом свойства 4 математического ожидания (см. гл. II)
но слагаемое этой суммы, у которого второй индекс равен і, т.е. 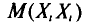
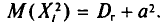
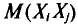
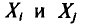
Так как имеется n-1 таких слагаемых, то
В силу свойства 1 дисперсии (см. гл. П) получаем
Нами уже найден (см. пп. 2 и 3):
Поэтому
Таким образом,
и не зависит от индекса суммирования і. Поэтому
Что и требовалось доказать.
В заключение этого пункта отметим, что если варианты 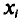
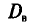
где С—ложный нуль.
Действительно, с учетом формулы (4.3) имеем
откуда
Пример:
Для выборки, указанной в примере 2 из п. 2, найдем 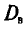
Наконец, согласно формуле (4.11)
Оценки параметров распределения
Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при 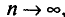
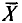
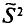
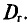
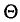
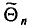
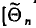
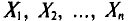
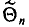
Несмещенной называют оценку 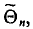
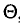
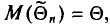
Пример:
Оценка 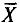
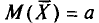
Пример:
Оценка 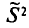
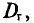
Пример:
Наряду с выборочной дисперсией 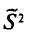
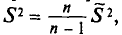
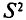
Таким образом, оценка 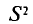
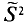
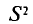
T. e.
Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения.
Состоятельной называют такую оценку 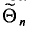
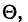
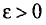
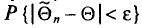
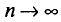
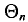
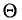
Очевидно, такому требованию должна удовлетворять всякая оценка, пригодная для практического использования.
Заметим, что несмещенная оценка 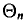
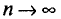
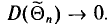
Пример:
Как было установлено (см. п. 3), 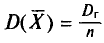
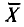
Можно показать, что несмещенная оценка 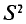
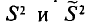
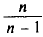
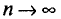
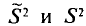
Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
Левые части формул (4.12), (4.13), в которых случайные величины 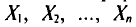
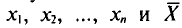
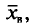
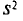
Отметим, что если варианты 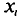
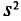
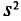
где С—ложный нуль.
Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.
Ясно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценка, обладающая таким свойством, называется эффективной.
Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.
Пример:
С плодового дерева случайным образом отобрано 10 плодов. Их массы 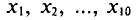
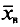
Следовательно,
Отсюда
Итак, оценка генеральной средней массы плода равна 243 г со средней квадратической ошибкой 9 г.
Оценка генерального среднего квадратического отклонения массы плода равна 28 г.
Пример:
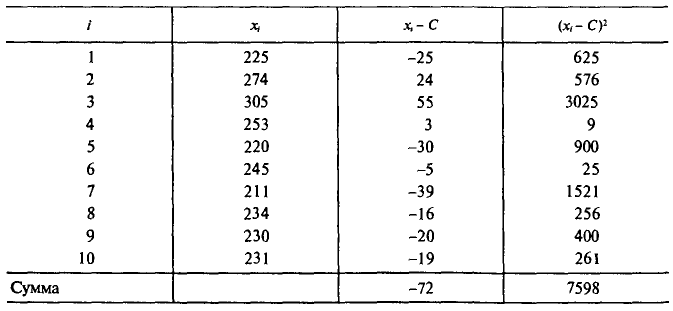
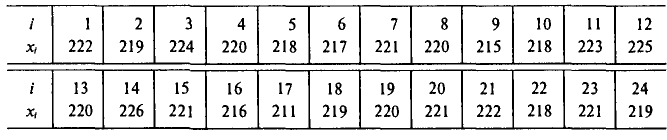
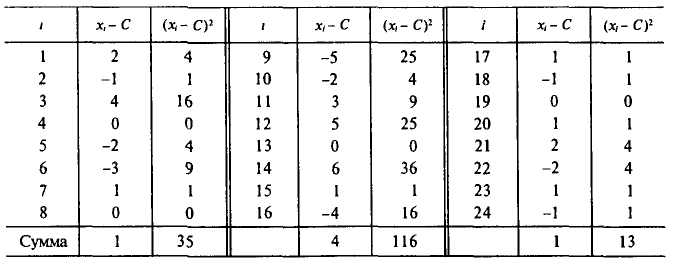
Через каждый час измерялось напряжение в электросети. Результаты измерений (в вольтах) представлены в следующей таблице:
Найти оценки для математического ожидания и дисперсии результатов измерений. Оценки для математического ожидания и дисперсии найдем по формулам (6) и (14), положив С=220. Все необходимые вычисления приведены в нижеследующей таблице:
Следовательно,
Доверительные интервалы для параметров нормального распределения
Пусть 

Если известно, что оценка 


Если же о распределении имеется какая-либо информация, то можно сделать больше.
Здесь речь будет идти об оценке параметров а и 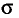
Пусть 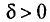
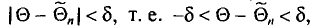
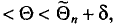
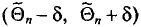


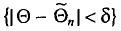
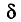
Определение:
Надежностью (доверительной вероятностью) оценки 

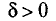

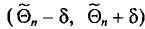

Заметим, что после того, как по данным выборки вычислена оценка 
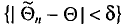
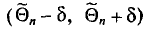




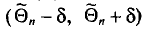

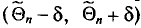


Иными словами, 
Ясно, что, чем меньше число 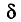

Определение:
Доверительным интервалом называется найденный по данным выборки интервал 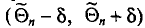


Надежность 
Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр 




Доверительный интервал для математического ожидания при известном
Доверительный интервал для математического ожидания при известном
В некоторых случаях среднее квадратическое отклонение о ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения осуществляются одним и тем же прибором при одних и тех же условиях.
Итак, пусть случайная величина X распределена нормально с параметрами а и 


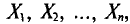

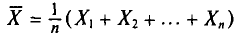
Потребуем, чтобы выполнялось соотношение 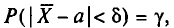

или
где
Найдя из равенства (4.15) 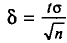
Так как Р задана и равна 
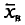
Смысл полученного соотношения таков: с надежностью у можно утверждать, что доверительный интервал 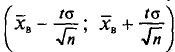
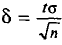
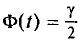
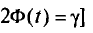
Как уже упоминалось, надежность 
Пример:
Признак X распределен в генеральной совокупности нормально с известным 

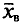
Для 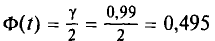
t=2,58. Следовательно, 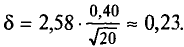
Доверительный интервал для математического ожидания при неизвестном
Доверительный интервал для математического ожидания при неизвестном 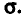
Пусть случайная величина X имеет нормальное распределение с неизвестными нам параметрами а и 
где n —объем выборки; 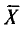

Плотность вероятности распределения Стьюдента дается формулой
где коэффициент 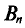
Потребуем, чтобы выполнялось соотношение
где 
Так как S(t, n) — четная функция от t, то, пользуясь формулой
(2.15) (см. § 2.5), получим
Отсюда
Следовательно, приходим к утверждению: с надежностью 
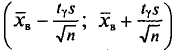
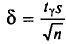
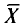
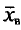
В приложении 4 приведена таблица значений 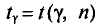
Заметим, что при 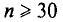
(см. § 2.7, п. 2). Это связано с тем, что
Пример. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 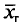

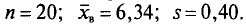

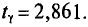
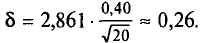
= 6,08 и 6,34 + 0,26 = 6,60. Итак, доверительный интервал (6,08; 6,60) покрывает 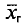
Доверительный интервал для среднего квадратического отклонения
Для нахождения доверительного интервала для среднего квадратического отклонения 
С надежностью 
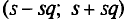

В приложении 5 приведена таблица значений 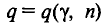

Пример:
Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 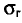

Для надежности 
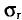
Пример:
На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратическое отклонение — 20 кг.
Определим: 1) доверительный интервал для математического ожидания а с надежностью 0,95; 2) доверительный интервал для среднего квадратического отклонения с той же надежностью.
При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.
Решение:
1) Согласно условиям задачи, 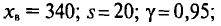
Пользуясь распределением Стьюдента, для надежности у=0,95 и n = 20 находим в таблице приложения 4 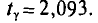
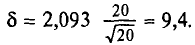
= 330,6 и 340 + 9,4 = 349,4. Итак, доверительный интервал (330,6; 349,4) покрывает а с надежностью 0,95.
Можно считать, что в данном случае истинная масса измерена 9 4 достаточно точно (отклонение порядка 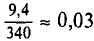
2) Для надежности у =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 20 * 0,37 = 7,4. Границы доверительного интервала 20 — 7,4 = 12,6 и 20 + 7,4 = 27,4. Таким образом, 12,6 < 

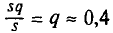
Примечание. Выше предполагалось, что q<1. Если q> 1, то, учитывая, что 

Пример:
Признак X генеральной совокупности распределен нормально. По выборке объема n = 10 найдено «исправленное» среднее квадратическое отклонение s = 0,16. Найдем доверительный интервал для 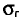
Для надежности у = 0,999 и n= 10 по таблице приложения 5 находим q=1,80.
Следовательно, искомый доверительный интервал таков’
или
Оценка истинного значения измеряемой величины
Пусть проводится n независимых равноточных измерений* некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины 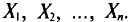
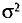

Пример:
По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений 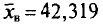
Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном 
покрывающего а с заданной надежностью у=0,99.
Пользуясь таблицей приложения 4 по у=0,99 и n = 9, находим
Найдем точность оценки:
Границы доверительного интервала
и
Итак, с надежностью у=0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719<а< 47,919.
Оценка точности измерений
В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения 

Пример:
По 16 независимым равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s=0,4. Найдем точность измерений с надежностью у = 0,99.
Как отмечено выше, точность измерений характеризуется средним квадратическим отклонением о случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала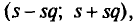

или
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_г=sqrt{D_г}]
Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
«Дисперсия: генеральная, выборочная, исправленная» 👇
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_в=sqrt{D_в}]
Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
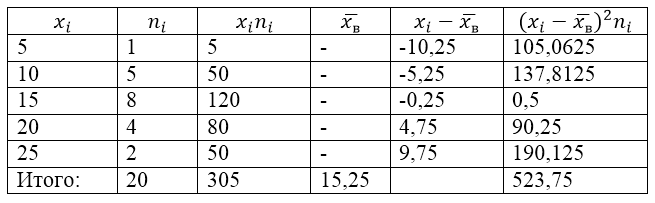
Для решения этой задачи для начала сделаем расчетную таблицу:
Рисунок 2.
Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
То есть
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Найдем выборочную дисперсию по формуле:
[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]
Выборочное среднее квадратическое отклонение:
[{sigma }_в=sqrt{D_в}approx 5,12]
Исправленная дисперсия:
[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]
Исправленное среднее квадратическое отклонение:
[S=sqrt{S^2}approx 5,25]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
Среднее абсолютное отклонение позволяет решить проблему, заключающуюся в том, что сумма отклонений от среднего равна нулю. Для этого при расчете среднего используется абсолютное значение отклонений.
Второй подход к расчету отклонений состоит в их возведении в квадрат.
Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии:
- Дисперсия определяется как среднее квадратов отклонений от среднего значения.
- Стандартное отклонение – это положительный квадратный корень дисперсии.
Далее обсуждается расчет и использования дисперсии и стандартного отклонения.
Дисперсия генеральной совокупности.
Если нам известен каждый элемент генеральной совокупности, мы можем вычислить дисперсию генеральной совокупности или просто дисперсию (англ. ‘population variance’).
Она обозначается символом (sigma^2)[сигма] и представляет собой среднее арифметическое квадратов отклонений от среднего значения.
Формула дисперсии генеральной совокупности.
( Large
sigma^2 = { dsum_{i=1}^{N} ( X_i – mu )^2 over N } ) (Формула 11)
где
- (mu) [мю] – это среднее генеральной совокупности, а
- (N) – размер генеральной совокупности.
Зная среднее значение μ, мы можем использовать Формулу 11 для вычисления суммы квадратов отклонений от среднего с учетом всех (N) элементов в генеральной совокупности, а затем для определения среднего квадратов отклонений путем деления этой суммы на (N).
Независимо от того, является ли отклонение от среднего положительным или отрицательным, возведение в квадрат этой разности дает положительное число.
Таким образом, дисперсия решает проблему отрицательных отклонений от среднего значения, устраняя их посредством операции возведения в квадрат этих отклонений.
Рассмотрим пример.
Прибыль в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год составляла 0.9%, 1.6% и 3.5% соответственно. Мы рассчитали среднюю прибыль в процентах от выручки как 2.0%.
Следовательно, дисперсия прибыли в процентах от выручки составляет:
(1/3)[(0.9 – 2.0)2 + (1.6 – 2.0)2 + (3.5 – 2.0)2]
= (1/3)(-1.12 + -0.42 + 1.52)
= (1/3)(1.21 + 0.16 + 2.25) = (1/3)(3.62) = 1.21
Стандартное отклонение генеральной совокупности.
Поскольку дисперсия измеряется в квадратах, нам нужен способ вернуться к исходным единицам. Мы можем решить эту проблему, используя стандартное отклонение, т.е. квадратный корень из дисперсии.
Стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в той же единице измерения, что и наблюдения.
Формула стандартного отклонения генеральной совокупности.
Стандартное отклонение генеральной совокупности (или просто стандартное отклонение, а также среднеквадратическое отклонение, от англ. ‘population standard deviation’), определяемое как положительный квадратный корень из дисперсии генеральной совокупности, составляет:
( Large dst
sigma = sqrt{sum_{i=1}^{N} ( X_i – mu )^2 over N} ) (Формула 12)
где
- (mu) [мю] – это среднее генеральной совокупности, а
- (N) – размер генеральной совокупности.
Используя пример прибыли в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год, в соответствии с Формулой 12, мы вычислим дисперсию 1.21, а затем возьмем квадратный корень: ( sqrt{1.21} ) = 1.10.
Как дисперсия, так и стандартное отклонение являются примерами параметров распределения. В последующих чтениях мы введем понятие дисперсии и стандартного отклонения как меры риска.
Занимаясь инвестициями, мы часто не знаем среднего значения интересующей совокупности, обычно потому, что мы не можем практически идентифицировать или провести измерения для каждого элемента генеральной совокупности.
Поэтому мы рассчитываем среднее значение по генеральной совокупности и среднее выборки, взятой из совокупности, и вычисляем выборочную дисперсию или стандартное отклонение выборки, используя формулы, немного отличающиеся от Формул 11 и 12.
Мы обсудим эти вычисления далее.
Однако в инвестициях у нас иногда есть определенная группа, которую мы можем считать генеральной совокупностью. Для четко определенных групп наблюдений мы используем Формулы 11 и 12, как в следующем примере.
Пример расчета стандартного отклонения для генеральной совокупности.
В Таблице 20 представлен годовой оборот портфеля из 12 фондов акций США, которые вошли в список Forbes Magazine Honor Roll 2013 года.
Журнал Forbes ежегодно выбирает американские взаимные фонды, отвечающие определенным критериям для своего почетного списка Honor Roll.
Критериями являются:
- сохранение капитала (эффективность на медвежьем рынке),
- непрерывность управления (у фонда должен управлять менеджер непрерывно, в течение не менее 6 лет), диверсификация портфелей,
- доступность (дисквалификация фондов, которые закрыты для новых инвесторов), и
- долгосрочные показатели эффективности после уплаты налогов.
Оборачиваемость или оборот портфеля, показатель торговой активности, является меньшим значением из стоимости продаж или покупок за год, деленным на среднюю чистую стоимость активов за год. Количество и состав списка Forbes Honor Roll меняются из года в год.
|
Фонд |
Годовой оборот портфеля (%) |
|---|---|
|
Bruce Fund (BRUFX) |
10 |
|
CGM Focus Fund (CGMFX) |
360 |
|
Hotchkis And Wiley Small Cap Value A Fund (HWSAX) |
37 |
|
Aegis Value Fund (AVALX) |
20 |
|
Delafield Fund (DEFIX) |
49 |
|
Homestead Small Company Stock Fund (HSCSX) |
1 |
|
Robeco Boston Partners Small Cap Value II Fund (BPSCX) |
32 |
|
Hotchkis And Wiley Mid Cap Value A Fund (HWMAX) |
72 |
|
T Rowe Price Small Cap Value Fund (PRSVX) |
9 |
|
Guggenheim Mid Cap Value Fund Class A (SEVAX) |
19 |
|
Wells Fargo Advantage Small Cap Value Fund (SSMVX) |
16 |
|
Stratton Small-Cap Value Fund (STSCX) |
11 |
Источник: Forbes (2013).
Основываясь на данных из таблицы 20, сделайте следующее:
- Рассчитайте среднее по совокупности для оборота портфеля за период, используя данные для 12 фондов из Honor Roll.
- Рассчитайте дисперсию и стандартное отклонение совокупности для оборота портфеля.
- Объясните использование формул в этом примере.
Решение для части 1:
(mu) = (10 + 360 + 37 + 20 + 49 + 1 + 32 + 72 + 9 + 19 + 16 + 11)/12
= 636 /12 = 53%.
Решение для части 2:
Установив, что (mu) = 53%, мы можем вычислить дисперсию
( sigma^2 = { sum_{i=1}^{N} ( X_i – mu )^2 over N } ), сначала рассчитав числитель, а затем разделив результат на (N) = 12.
Числитель (сумма квадратов отклонений от среднего) равен:
(10 – 53)2 + (360 – 53)2 + (37 – 53)2 + (20 – 53)2 +
(49 – 53)2 + (1 – 53)2 + (32 – 53)2 + (72 – 53)2 +
(9 – 53)2 + (19 – 53)2 + (16 – 53)2 + (11 – 53)2 = 107,190
Таким образом,
( sigma^2 ) = 107,190/12 = 8,932.50.
Для расчета стандартного отклонения находим квадратный корень:
( sigma = sqrt{ 8,932.50 } ) = 94.51%.
Единицей измерения дисперсии является процент в квадрате, поэтому единицей измерения стандартного отклонения также является процент.
Решение для части 3:
Если генеральная совокупность четко определена как фонды Forbes Honor Roll за один конкретный год (2013 г.), и если под оборотом портфеля понимается конкретный одногодичный период, о котором отчитывается Forbes, то применение формул генеральной совокупности для дисперсии и стандартного отклонения уместно.
Результаты 8,932.50 и 94.51 представляют собой, соответственно, перекрестную дисперсию и стандартное отклонение годового оборота портфеля для фондов Forbes Honor Roll за 2013 год.
Фактически, мы не могли должным образом использовать фонды Honor Roll для оценки дисперсии оборота портфеля (например) любой другой по-разному определенной генеральной совокупности, потому что фонды Honor Roll не являются случайной выборкой из какой-либо большей генеральной совокупности взаимных фондов США.
Выборочная дисперсия.
Во многих случаях в управлении инвестициями подгруппа или выборка из генеральной совокупности – это все, что мы можем наблюдать. Когда мы имеем дело с выборками, сводные показатели называются статистикой.
Статистика, которая измеряет дисперсию по выборке, называется выборочной дисперсией или дисперсией выборки (англ. ‘sample variance’).
В приведенном ниже обсуждении обратите внимание на использование латинских букв вместо греческих для обозначения объема выборки.
Формула выборочной дисперсии.
( Large
s^2 = { dsum_{i=1}^{n} ( X_i – overline X )^2 over n-1 } ) (Формула 13)
где
- ( overline X ) – среднее значение выборки, а
- (n) – количество наблюдений в выборке.
Формула 13 предписывает нам предпринять следующие шаги для вычисления выборочной дисперсии:
- Рассчитать выборочное среднее значение, ( overline X ).
- Рассчитать квадратичное отклонение каждого наблюдения от среднего значения по выборке, ( ( X_i – overline X )^2 )
- Найти сумму квадратов отклонений от среднего: ( sum_{i=1}^{n} ( X_i – overline X )^2 ).
- Разделить сумму квадратов отклонений от среднего на ( (n – 1)).
Мы проиллюстрируем расчет выборочной дисперсии и выборочного стандартного отклонения на примере ниже.
Отличие выборочной дисперсии от дисперсии генеральной совокупности.
Мы используем обозначение ( s^2 ) для выборочной дисперсии, чтобы отличить ее от дисперсии генеральной совокупности ( sigma^2 ).
Формула для выборочной дисперсии почти такая же, как и для дисперсии генеральной совокупности, за исключением использования среднего значения выборки ( overline X ) вместо среднего значения генеральной совокупности μ и другого делителя.
В случае дисперсии генеральной совокупности мы делим числитель на размер совокупности (N). Однако для дисперсии выборки мы делим ее на размер выборки минус 1 или (n – 1). Используя (n – 1) (а не (n)) в качестве делителя мы улучшаем статистические свойства выборочной дисперсии.
В статистических терминах выборочная дисперсия, определенная в Формуле 13, является несмещенной оценкой (англ. ‘unbiased estimator ‘) дисперсии генеральной совокупности ( sigma^2 ).
Мы обсудим эту концепцию далее в чтении о выборке.
Величина (n – 1) также называется числом степеней свободы (англ. ‘number of degrees of freedom’) при оценке дисперсии генеральной совокупности.
Чтобы оценить дисперсию ( s^2 ), мы должны сначала вычислить среднее. После того как мы вычислили среднее значение выборки, существует только (n – 1) независимых отклонений от него.
Стандартное отклонение выборки.
Для стандартного отклонения генеральной совокупности мы аналогичным образом можем вычислить стандартное отклонение выборки, взяв квадратный корень из положительной дисперсии выборки.
Формула стандартного отклонения выборки.
Стандартное отклонение выборки (выборочное стандартное отклонение, выборочное среднеквадратическое отклонение, англ. ‘sample standard deviation’), обозначается символом (s) и рассчитывается следующим образом:
( Large dst
s = sqrt{ sum_{i=1}^{n} ( X_i – overline X )^2 over n-1 } ) (Формула 14)
где
- ( overline X ) – среднее значение выборки, а
- (n) – количество наблюдений в выборке.
Чтобы рассчитать стандартное отклонение выборки, мы сначала вычисляем дисперсию выборки, используя приведенные выше шаги. Затем мы берем квадратный корень из выборочной дисперсии.
Пример, приведенный ниже, иллюстрирует расчет выборочной дисперсии и стандартного отклонения выборки для двух взаимных фондов, представленных ранее.
Пример расчета выборочной дисперсии и стандартного отклонения выборки.
После расчета геометрических и арифметических средних доходностей двух взаимных фондов в Примере (1) мы вычислили две меры дисперсии для этих фондов, размах и среднее абсолютное отклонение доходности (см. Пример расчета размаха и среднего абсолютного отклонения для оценки риска).
Теперь мы вычислим выборочную дисперсию и стандартное отклонение выборки для доходности тех же двух фондов.
|
Год |
Фонд Selected |
Фонд T. Rowe Price |
|---|---|---|
|
2008 |
-39.44% |
-35.75% |
|
2009 |
31.64 |
25.62 |
|
2010 |
12.53 |
15.15 |
|
2011 |
-4.35 |
-0.72 |
|
2012 |
12.82 |
17.25 |
Источник: performance.morningstar.com.
На основании приведенных выше данных сделайте следующее:
- Рассчитайте выборочную дисперсию доходности для (A) SLASX и (B) PRFDX.
- Рассчитайте выборочное стандартное отклонение доходности для (A) SLASX и (B) PRFDX.
- Сравните дисперсию доходности, измеренную стандартным отклонением доходности и средним абсолютным отклонением доходности для каждого из двух фондов.
Решение для части 1:
Чтобы вычислить выборочную дисперсию, мы используем Формулу 13 (значения отклонений приведены в процентах).
А. SLASX:
1. Среднее значение выборки:
( overline R ) = (-39.44 + 31.64 + 12.53 – 4.35 +12.82)/ 5 =
13.20/5 = 2.64%.
2. Квадратичные отклонения от среднего значения:
(-39.44 – 2.64)2 = (-42.08)2 = 1,770.73
(31.64 – 2.64)2 = (29.00)2 = 841.00
(12.53 – 2.64)2 = (9.89)2 = 97.81
(-4.35 – 2.64)2 = (-6.99)2 = 48.86
(12.82 – 2.64)2 = (10.18)2 = 103.63
3. Сумма квадратов отклонений от среднего составляет:
1,770.73 + 841.00 + 97.81 + 48.86 + 103.63 = 2,862.03.
4. Разделим сумму квадратов отклонений от среднего на (n – 1):
2,862.03 / (5 – 1) = 2,862.03 / 4 = 715.51
B. PRFDX:
1. Среднее значение выборки:
( overline R ) = (-35.75 + 25.62 + 15.15 – 0.72 + 17.25)/5 = 21.55/5 = 4.31%.
2. Квадратичные отклонения от среднего значения:
(-35.75 – 4.31)2 = (-40.06)2 = 1,604.80
(25.62 – 4.31)2 = (21.31)2 = 454.12
(15.15 – 4.31)2 = (10.84)2 = 117.51
(-0.72 – 4.31)2 = (-5.03)2 = 25.30
(17.25 – 4.31)2 = (12.94)2 = 167.44
3. Сумма квадратов отклонений от среднего составляет:
1,604.80 + 454.12 + 117.51 + 25.30 + 167.44 = 2,369.17.
4. Разделим сумму квадратов отклонений от среднего на ((n – 1)):
2,369.17/4 = 592.29
Решение для части 2:
Чтобы найти стандартное отклонение, мы берем положительный квадратный корень из дисперсии.
A. Для SLASX, s = ( sqrt {715.51} ) = 26.7%.
B. Для PRFDX, s = ( sqrt {592.29} ) = 24.3%.
Решение для части 3:
Таблица 21 суммирует результаты части 2 для стандартного отклонения и включает результаты для MAD из Примера расчета размаха и среднего абсолютного отклонения для оценки риска.
|
Фонд |
Стандартное |
Среднее |
|---|---|---|
|
SLASX |
26.7 |
19.6 |
|
PRFDX |
24.3 |
18.0 |
Обратите внимание, что среднее абсолютное отклонение меньше стандартного отклонения. Среднее абсолютное отклонение всегда будет меньше или равно стандартному отклонению, потому что стандартное отклонение придает больший вес большим отклонениям, чем маленьким (помните, что отклонения возводятся в квадрат).
Поскольку стандартное отклонение является мерой дисперсии относительно среднего арифметического, мы обычно представляем среднее арифметическое и стандартное отклонение вместе при анализе данных.
Когда мы имеем дело с данными, которые представляют собой временной ряд процентных изменений, представление геометрического среднего, представляющего собой сложную ставку скорости роста, также очень полезно.
В Таблице 22 представлены исторические геометрические и арифметические средние доходности, а также историческое стандартное отклонение доходности для годовой и месячной доходности S&P 500.
Мы представляем эту статистику для номинальной (без поправки на инфляцию) доходности, чтобы мы могли наблюдать первоначальные величины доходности.
|
Ставка доходности |
Геометрическое |
Среднее |
Стандартное отклонение |
|---|---|---|---|
|
S&P 500 (Годовая) |
9.84 |
11.82 |
20.18 |
|
S&P 500 (Месячная) |
0.79 |
0.94 |
5.50 |
Источник: Ibbotson.
Дисперсия выборки и дисперсия населения: в чем разница?
17 авг. 2022 г.
читать 2 мин
Дисперсия — это способ измерения разброса значений в наборе данных.
Формула для расчета дисперсии населения :
σ 2 = Σ (xi – μ) 2 / N
куда:
- Σ : символ, означающий «сумма».
- μ : Среднее значение населения
- x i : i -й элемент из совокупности
- N : Численность населения
Формула для расчета выборочной дисперсии :
s 2 = Σ (x i – x ) 2 / (n-1)
куда:
- x : выборочное среднее
- x i : i -й элемент из выборки
- n : размер выборки
Обратите внимание, что между двумя формулами есть только одна крошечная разница:
Когда мы вычисляем дисперсию населения, мы делим на N (размер населения).
Когда мы вычисляем выборочную дисперсию, мы делим на n-1 (размер выборки — 1).
При расчете выборочной дисперсии мы применяем так называемую поправку Бесселя, которая представляет собой действие деления на n-1.
Не вдаваясь в математические детали, можно показать, что деление на n-1 дает объективную оценку дисперсии генеральной совокупности, которая в любом случае представляет собой значение, которое нас обычно интересует.
Когда рассчитывать дисперсию выборки по сравнению с дисперсией генеральной совокупности
Если вы не уверены, следует ли вам рассчитывать дисперсию выборки или дисперсию генеральной совокупности, помните об этом эмпирическом правиле:
Вы должны рассчитать выборочную дисперсию , когда набор данных, с которым вы работаете, представляет собой выборку, взятую из большей интересующей совокупности.
Вы должны вычислить дисперсию совокупности , когда набор данных, с которым вы работаете, представляет всю совокупность, то есть каждое значение, которое вас интересует.
В следующих примерах показаны различные сценарии расчета выборочной дисперсии по сравнению с дисперсией генеральной совокупности.
Пример: расчет выборочной дисперсии
Предположим, ботаник хочет рассчитать разницу в высоте определенного вида растений. Поскольку в одном регионе растут тысячи отдельных растений, она решает взять простую случайную выборку из 20 растений и измерить высоту каждого из них.
В этом сценарии ботаник должен вычислить дисперсию выборки , потому что он заинтересован в дисперсии всей популяции растений, но просто использует эту выборку для оценки истинной дисперсии популяции.
Пример: расчет дисперсии населения
Предположим, учитель хочет рассчитать дисперсию экзаменационных баллов для 20 учеников в ее классе.
В этом сценарии учитель должен вычислить дисперсию генеральной совокупности , поскольку набор данных, с которым она работает (20 баллов за экзамен), представляет всю интересующую ее совокупность.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать выборочную дисперсию и дисперсию генеральной совокупности в различных статистических программах:
Как рассчитать выборку и дисперсию населения в Excel
Как рассчитать выборку и дисперсию населения в R
Как рассчитать выборку и дисперсию населения в Python