В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx – Ax; By – Ay} |
| Для трехмерных задач | AB = {Bx – Ax; By – Ay; Bz – Az} |
| Для n-мерных векторов | AB = {B1 – A1; B2 – A2; … Bn – An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Длина вектора
Как найти?
Длина вектора $ overline{a}$ обозначается как $ |overline{a}| $. Как найти длину вектора по его координатам? Для этого существует две формулы в зависимости от расположения вектора: на плоскости $ overline{a}=(a_x;a_y) $ или в пространстве $ overline{a} = (a_x; a_y; a_z) $.
Формула длины вектора на плоскости:
$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2} $$
Формула длины вектора в пространстве:
$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2 + a_z ^2 } $$
Если даны координаты точек начала и конца вектора $ A(a_x; a_y) $ и $ B(b_x; b_y) $, то найти длину можно по формулам:
$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y) ^2} $$
$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y)^2+ (a_z-b_z)^2} $$
Примеры решений
| Пример 1 |
| Найти длину вектора по его координатам $ overline{a} = (4;-3) $ |
| Решение |
|
Разберем вектор. Первая координата $ a_x = 4 $, а вторая координата $ a_y=-3 $. Так как даны две координаты, то делаем вывод, что задача плоская. Необходимо применить первую формулу. Подставляем в неё значения из условия задачи: $$|overline{a}| = sqrt{4^2+(-3)^2} = sqrt{16+9} = sqrt{25} = 5 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Длина вектора $|overline{a}| = 5 $ |
| Пример 2 |
| Найти длину вектора по координатам $ overline{a}=(4;2;4) $ |
| Решение |
|
Сразу замечаем, что дана пространственная задача. А именно $ a_x=4, a_y=2, a_z=4 $. Для нахождения длины вектора используем вторую формулу. Подставляем неизвестные в неё: $|overline{a}|=sqrt{4^2+2^2+4^2}=sqrt{36}=6 $ |
| Ответ |
| Длина вектора $|overline{a}|=6 $ |
| Пример 3 |
| Найти длину вектора, если известны координаты его начала и конца. $ A=(2;1), B=(-1;3) $ |
| Решение |
|
Задача дана плоская судя по наличию только двух координат у векторов. Но даны на этот раз начало и конец вектора. Поэтому сначала находим координаты вектора $ overline{AB} $, а только потом его длину по формуле координат: $ overline{AB}=(b_x-a_x;b_y-a_y)=(-1-2;3-1)=(-3;2) $ Теперь когда координаты вектора $ overline{AB} $ стали известны можно использовать привычную формулу: $|overline{AB}|=sqrt{(-3)^2+2^2}=sqrt{9+4}=sqrt{13} $ |
| Ответ |
| $|overline{AB}|=sqrt{13} $ |
В статье мы ответили на вопрос:”Как найти длину вектора?” с помощью формул. А также рассмотрели практические примеры решения задач на плоскости и в пространстве. Следует заметить, что существуют аналогичные формулы для пространств больше, чем трёхмерные.
Онлайн калькулятор для нахождения координат вектора на плоскости по двум или по трём точкам в пространстве.
Чтобы узнать координаты вектора в плоскости (i,j) или найти координаты вектора в пространстве (i,j,k), необходимо произвести ряд однотипных вычислений на основе координат точек его начала и конца.
Предположим, нам дана точка начала вектора A с координатами (1;2) и точка конца вектора с координатами B(3;5). Для того чтобы рассчитать координаты самого вектора необходимо отнять координату начала от координаты конца вдоль каждой оси.
[ bar{i}=x_{2}-x_{1}=3-1=2 ]
[ bar{j}=y_{2}-y_{1}=5-2=3 ]
Таким образом, координатами вектора становятся (2;3), причем порядок расположения координат строго соблюдается. Аналогично происходит, если отталкиваться от координат в пространстве (x,y,z).
[ A(0;3;1) ]
[ B(2;2;1) ]
[ bar{i}=x_{2}-x_{1}=2-0=2 ]
[ bar{j}=y_{2}-y_{1}=2-3=-1 ]
[ bar{k}=z_{2}-z_{1}=1-1=0 ]
Координаты вектора: [ = (2,-1,0) ]
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Длина вектора – основные формулы
Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
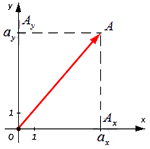
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.
От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.
Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.
Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.
Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.
Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e
Ответ: a→=49+e.
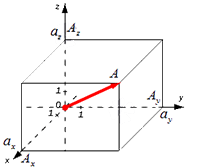
Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.
Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.
Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ – орты прямоугольной системы координат.
Решение
Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.
Ответ:a→=52.
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2
А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле
AB→=(bx-ax)2+(by-ay)2+(bz-az)2
Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.
Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-
Ответ: AB→=20-23.
Определить, при каких значениях длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .
Решение
Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2
Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:
26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2 λ1=-2, λ2=2, λ3=0.
Ответ: λ1=-2, λ2=2, λ3=0.
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.
Решение
Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.
Ответ:BC→=37.
Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Задача 63489 Найдите координаты вектора (2АВ +ВС),…
Условие
Найдите координаты вектора (2АВ +ВС), если А(4;0;2) , В(0;0;1) , С(3;5;–2)
математика 10-11 класс
1626
Решение
★
vector{AB}=(0-4;0-0;1-2)=(-4;0;-1)
vector{BС}=(3-0;5-0;-2-1)=(3;5;-3)
Умножение вектора на число 2 – умножение каждой координаты на число
2*vector{AB}=(-8;0;-2)
Сложение двух векторов выполняются [i]покоординатно[/i], т.е складываем первые координаты, складываем вторые координаты и складываем третьи координаты :
2*vector{AB}+vector{BС}=(-8;0;-2)+(3;5;-3)=(-8+3;0+5;-2+(-3))=[b](-5;5;-5)[/b]