Вектор мат ожидания как найти

Материал из MachineLearning.

Перейти к: навигация, поиск

Математическое ожидание — мера среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через (например, от англ. Expected value или нем. Erwartungswert), в русской (возможно, от англ. Mean value).

Определение

Пусть задано вероятностное пространство и определённая на нём случайная величина . Тогда, если существует интеграл Лебега от по пространству , то он называется математическим ожиданием, или средним значением, и обозначается или .

Основные формулы для математического ожидания

• Если  — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:

.

Математическое ожидание дискретного распределения

• Если  — дискретная случайная величина, имеющая распределение

,

то прямо из определения интеграла Лебега следует, что

.

Математическое ожидание целочисленной величины

• Если  — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей

то её математическое ожидание может быть выражено через производящую функцию последовательности

как значение первой производной в единице: . Если математическое ожидание бесконечно, то и мы будем писать

Теперь возьмём производящую функцию последовательности «хвостов» распределения

Эта производящая функция связана с определённой ранее функцией свойством: при .
Из этого по теореме о среднем (формуле конечных приращений) следует, что математическое ожидание равно просто значению этой функции в единице:

Математическое ожидание абсолютно непрерывного распределения

• Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью , равно

.

Математическое ожидание случайного вектора

Пусть  — случайный вектор. Тогда по определению

,

то есть математическое ожидание вектора определяется покомпонентно.

Математическое ожидание преобразования случайной величины

Пусть  — борелевская функция, такая что случайная величина имеет конечное математическое ожидание. Тогда для него справедлива формула:

,

если имеет дискретное распределение;

,

если имеет абсолютно непрерывное распределение.

Если распределение случайной величины общего вида, то

.

В специальном случае, когда , Математическое ожидание называется -тым моментом случайной величины.

Простейшие свойства математического ожидания

• Математическое ожидание числа есть само число.

 — константа;

• Математическое ожидание линейно, то есть

,

где  — случайные величины с конечным математическим ожиданием, а  — произвольные константы;

;

• Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если почти наверное, то

.

• Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий

.

Дополнительные свойства математического ожидания

• Неравенство Маркова.

Пусть случайная величина определена на вероятностном пространстве , и её математическое ожидание конечно. Тогда

,

где .

• Теорема Леви о монотонной сходимости.

Пусть  — монотонная последовательность неотрицательных почти наверное интегрируемых случайных величин. Тогда

.

• Теорема Лебега о мажорируемой сходимости.

Пусть есть сходящаяся почти наверное последовательность случайных величин: почти наверное. Пусть в дополнение существует интегрируемая случайная величина , такая что почти наверное. Тогда случайные величины интегрируемы и

.

• Тождество Вальда.

Пусть — независимые одинаково распределенные случайные величины. — также является случайной величиной имеющей дискретное распределение и принимающая положительные целые значения. Далее, и должны иметь конечное математическое ожидание и должно быть независимым от . Тогда

.

• Лемма Фату.

Пусть есть неотрицательная последовательность интегрируемых случайных величин . Тогда выполняется следующее неравенство для нижних пределов:

.

Примеры

• Пусть случайная величина имеет дискретное равномерное распределение, то есть Тогда её математическое ожидание

равно среднему арифметическому всех принимаемых значений.

.

• Пусть случайная величина имеет стандартное распределение Коши. Тогда

,

то есть математическое ожидание не определено.

Литература

• В.Феллер Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition. — 2-е изд. — М.: Мир, 1964. — С. 270—272.

Как найти математическое ожидание?

Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание – это первый начальный момент заданной СВ.

Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины – срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).

Формула среднего случайной величины

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$: $$ M(X)=sum_^. $$ Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$

Пример нахождения математического ожидания

Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.

Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом: $$ x_i quad -1 quad 2 quad 5 quad 10 quad 20 \ p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1 $$

Используем формулу для м.о. дискретной случайной величины: $$ M(X)=sum_^. $$ Получаем: $$ M(X)=sum_^ =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8. $$ Вот в этом примере 2 описано также нахождение дисперсии Х.

Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.

Используем для нахождения мат. ожидания формулу: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$ Подставляем из условия плотность вероятности и вычисляем значение интеграла: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx = int_<0>^ <1>12(x^2-x^3) cdot x dx = int_<0>^ <1>12(x^3-x^4) dx = \ =left.(3x^4-frac<12><5>x^5) right|_0^1=3-frac<12> <5>= frac<3><5>=0.6. $$

Вычисление математического ожидания онлайн

Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку “Вычислить”.
• Калькулятор покажет вычисленное математическое ожидание $M(X)$.

Видео. Полезные ссылки

Видеоролики: что такое среднее (математическое ожидание)

Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по терверу. Для закрепления материала – еще примеры решений по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

3.3 Математические ожидания и ковариации векторов и матриц

3.3. Математические ожидания и ковариации векторов и матриц

При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.

В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:

у= и e=.

Значения i-й переменной у_i (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной e_i случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.

При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.

Математическое ожидание вектора у размеров пх1 случайных переменных y₁, y₂, . у_п определяется как вектор их ожидаемых значений:

Е(у)=Е===y, (3.3.1)

Рекомендуемые файлы

где E(у_i)=y_i получается в виде E(у_i)=, используя функцию f_i(у_i) плотности вероятности безусловного распределения переменной у_i.

Если х и у – векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:

Пусть у_ij (i=1, 2, . m; j=1, 2, . п) набор случайных переменных с ожидаемыми значениями E(у_ij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(y_ij) размеров mхп следующим образом:

Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов

По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:

E(Y)==. (3.3.3)

Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.

Теорема 3.3.1. Если матрицы А=(а_ij) размеров lхm, B=(b_ij) размеров nхp, С=(c_ij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то

Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]

Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у – векторы случайных переменных размеров пх1, то

Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр – все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то

Ковариации и дисперсии

Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.

Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов

Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация

Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1

=E

=Е

=.

=. (3.3.4)

E[(y–y)(y–y) T ]=. (3.3.5)

Дисперсии s₁₁, s₂₂, . s_пп переменных y₁, y₂, . у_п и их ковариации s_ij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:

S=D(у)= (3.3.6)

В матрице S i-я строка содержит дисперсию переменной у_i и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением s_ij, используем для дисперсий s_ii=s_i 2 , где i =1, 2, . n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(у_i, у_j)=s_ij для двух переменных.

Матрица S дисперсий и ковариаций симметричная, так как s_ij=s_ji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.

Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1

=E

=E

=.

=.

Как следует из определения 3.3.3,

что после подобного сделанному в (3.2.4) преобразованию приводится к выражению

Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).

Пример 3.3.1. Если а – какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то

Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма у Т Ау>0. В дальнейшем будет использоваться часто следующая теорема.

Теорема 3.3.3. Если у – вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что а Т у=b для любого у, то D(у)=S – положительно определенная матрица.

Доказательство этой теоремы дано в [Себер (1980) стр.22].

Обобщенная дисперсия и нормированный вектор

Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:

Обобщенная дисперсия =det(S). (3.3.9)

В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=Y T (I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y₁, y₂, …, y_k], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:

Обобщенная выборочная дисперсия =det(S). (3.3.10)

Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора , чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y₁, y₂. у_п вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].

Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде

Использование матрицы S –1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S –1 =S –1/2 S –1/2 . Отсюда

где z=S –1/2 (у–y) – вектор нормированных случайных переменных. Математическое ожидание вектора z получается

и его дисперсия

Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S –1/2 (у–y) имеет нормальное распределение N(0, I).

Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у–) Т S –1 (у–) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у–) Т S –1 (у–)=а 2 , центрированный вектором и базирующийся на S –1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у–) Т S –1 (у–) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)] 1/2 . Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.

Математическое ожидание

Математическое ожидание — это ожидаемый результат от какого-то действия.

Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.

Случайная величина может быть двух типов:

1. Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
2. Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.

Математическое ожидание дискретной случайной величины рассчитывается этой формулой:

Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет “1” — 1/6, “2” — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).

Для непрерывной случайной величины используется эта формула:

В этом случае рассчитывается интеграл в заданном интервале.

Примеры вычисления математического ожидания

• если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
• если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.

Пример 1

Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:

xi	−1	1	2	3	4
pi	0,1	0,2	0,3	0,1	0,3

Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2

Пример 2

Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.

Используется формула для непрерывной случайной величины:

Пример 3

Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:

xi	1	2	3	4	5
pi	0,3	0,3	0,1	0,1	0,2

Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6

Пример 4

Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.

Используется формула для непрерывной случайной величины:

[spoiler title=”источники:”]

http://studizba.com/lectures/47-matematika/680-statisticheskie-metody-eksperimentalnyh-issledovaniy/13066-33-matematicheskie-ozhidaniya-i-kovariacii-vektorov-i-matric.html

http://www.uznaychtotakoe.ru/matematicheskoe-ozhidanie/

[/spoiler]

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 октября 2021 года; проверки требуют 7 правок.

Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины^[1]. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения (более строгие определения см. ниже). Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.

Обозначается через ^[2] (например, от англ. Expected value или нем. Erwartungswert);
в русскоязычной литературе также встречается обозначение (возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение .

Для случайной величины, принимающей значения только 0 или 1 математическое ожидание равно p — вероятности «единицы». Математическое ожидание суммы таких случайных величин равно np, где n — количество таких случайных величин. При этом вероятности появления определенного кол-ва единиц рассчитываются по биномиальному распределению. Поэтому в литературе, скорее всего, легче найти запись, что мат. ожидание биномиального распределения равно np^[3].

Некоторые случайные величины не имеют математического ожидания, например, случайные величины, имеющие распределение Коши.

На практике математическое ожидание обычно оценивается как среднее арифметическое наблюдаемых значений случайной величины (выборочное среднее, среднее по выборке). Доказано, что при соблюдении определенных слабых условий (в частности, если выборка является случайной, то есть наблюдения являются независимыми) выборочное среднее стремится к истинному значению математического ожидания случайной величины при стремлении объема выборки (количества наблюдений, испытаний, измерений) к бесконечности.

Определение[править | править код]

Общее определение через интеграл Лебега[править | править код]

Пусть задано вероятностное пространство и определённая на нём случайная величина . То есть, по определению,  — измеримая функция. Если существует интеграл Лебега от по пространству , то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается или .

Определение через функцию распределения случайной величины[править | править код]

Если  — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:

, .

Определение для абсолютно непрерывной случайной величины (через плотность распределения)[править | править код]

Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью , равно

.

Определение для дискретной случайной величины[править | править код]

Если  — дискретная случайная величина, имеющая распределение

, ,

то прямо из определения интеграла Лебега следует, что

.

Математическое ожидание целочисленной величины[править | править код]

• Если  — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей

, , ,

то её математическое ожидание может быть выражено через производящую функцию последовательности

как значение первой производной в единице: . Если математическое ожидание бесконечно, то и мы будем писать

Теперь возьмём производящую функцию последовательности «хвостов» распределения

,

Эта производящая функция связана с определённой ранее функцией свойством: при . Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:

Математическое ожидание случайного вектора[править | править код]

Пусть  — случайный вектор. Тогда по определению

,

то есть математическое ожидание вектора определяется покомпонентно.

Математическое ожидание преобразования случайной величины[править | править код]

Пусть  — борелевская функция, такая что случайная величина имеет конечное математическое ожидание. Тогда для него справедлива формула

если имеет дискретное распределение;

если имеет абсолютно непрерывное распределение.

Если распределение случайной величины общего вида, то

В специальном случае, когда , математическое ожидание называется -м моментом случайной величины.

Свойства математического ожидания[править | править код]

• Математическое ожидание числа (не случайной, фиксированной величины, константы) есть само число.

 — константа;

• Математическое ожидание линейно^[4], то есть

,

где  — случайные величины с конечным математическим ожиданием, а  — произвольные константы;

В частности, математическое ожидание суммы (разности) случайных величин равно сумме (соответственно — разности) их математических ожиданий.

.

• Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если почти наверняка, то

.

• Математическое ожидание произведения двух независимых или некоррелированных^[5] случайных величин равно произведению их математических ожиданий

.

Неравенства, связанные с математическим ожиданием[править | править код]

Неравенство Маркова — для неотрицательной случайной величины определённой на вероятностном пространстве с конечным математическим ожиданием выполняется неравенство:

, где .

Неравенство Йенсена для математического ожидания выпуклой функции от случайной величины. Пусть  — вероятностное пространство,  — определённая на нём случайная величина,  — выпуклая борелевская функция, такие, что , то

.

Теоремы, связанные с математическим ожиданием[править | править код]

.

.

Примеры[править | править код]

• Пусть случайная величина имеет дискретное равномерное распределение, то есть Тогда её математическое ожидание

равно среднему арифметическому всех принимаемых значений.

.

• Пусть случайная величина имеет стандартное распределение Коши. Тогда

,

то есть математическое ожидание не определено.

См. также[править | править код]

• Дисперсия случайной величины
• Моменты случайной величины
• Условное математическое ожидание

Примечания[править | править код]

Литература[править | править код]

• Феллер В. Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition / Перевод с англ. Р. Л. Добрушина, А. А. Юшкевича, С. А. Молчанова Под ред. Е. Б. Дынкина с предисловием А. Н. Колмогорова. — 2-е изд. — М.: Мир, 1964. — С. 270—272.

Ссылки[править | править код]

• Математическое ожидание и его свойства на http://www.toehelp.ru

Савельев Ф. Г.

Гр. 2351

Вариант 19.

Дано:

1. Вычисление вектора мат. Ожиданий и
   ковариационных характеристик С.В.

Сначала найдём неизвестную константу.
Для этого вычислим плотность распределения
одной из компонент случайного вектора
с учётом неизвестной константы C
и приравняем её к единице.

.

Найдём вектор математических ожиданий

Имеем:
.

Плотность распределения
:

Плотность распределения
:

Отсюда,
–
вектор мат. ожиданий.

Ковариационную матрицу мы можем найти
двумя способами

1-ый способ. Ковариационная матрица
– это матрица, обратная матрице
квадратичной формы.

Матрица квадратичной формы:
;

Матрица ковариации:
.

2-ой способ. Найдем первый и четвертый
элемент матрицы ковариации – это
дисперсии компонент случайного вектора
x и y
соответственно.

,

Остается найти второй и третий члены
матрицы. Они, как известно, равны между
собой и вычисляются по формуле:
.

Найдем
.

Тогда второй и третий элементы будут
равны:
.

Имеем матрицу ковариации:
,
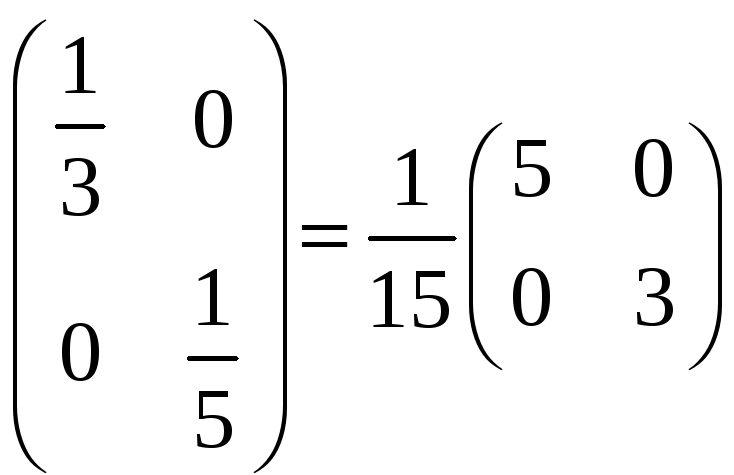что полностью совпало с вычисленным
первым способом.

1. Найти ортогональное преобразование,
   переводящее соответствующий центрированный
   случайный вектор в вектор с независимыми
   компонентами.
   

Преобразование будет называться
ортогональным, если его матрица будет
ортогональна т. е.

Тогда само преобразование можно описать
формулой

– матрица

– вектор при этом матрица

должна быть ортогональной.

Однако нам в задании уже дана плотность
с независимыми компонентами, следовательно
для перевода данного случайного вектора
в центрированный вектор необходим лишь
сдвиг. Опишем общий вид данного
преобразования.

Матрица

– матрица перехода от стандартного
базиса к базису собственных векторов
нашей матрицы квадратичной формы.

Матрица квадратичной формы

уже диагональная и собственные числа
равны, соответственно,

Матрица перехода будет

– единичная матрица. Эта матрица
ортогональна, следовательно, ортогонально
и преобразование. Для центрирования
данного случайного вектора необходимо
просто отнять столбец математических
ожиданий данных компонент.

Произведём первую замену. Вместе
,

подставляем новые координаты

Тогда квадратичная форма будет следующей

Якобиан такой замены будет равен 1

Следовательно, после такой замены,
плотность случайного вектора принимает
вид

Данный вектор центрирован (математическое
ожидание обоих компонент равно 0), имеет
независимые друг от друга компоненты
и получен ортогональным преобразованием.

Из такого вектора легко получить
стандартный нормальный вектор. Достаточно
сделать ещё одну замену. Вместо
,

ставим

На диагонали всегда будут находиться
члены вида
.
Якобиан такой замены также можно очень
просто посчитать

И умножив плотность распределения

т. е. компонент предыдущей замены получим

плотность распределения стандартного
и центрированного вектора.

4. Вычислить характеристики совместного
распределения с.в.
и
записать его плотность.

Математические ожидания мы находим,
используя свойство его линейности.

Пусть
,
тогда
,

.

Находим новые дисперсии, используя
свойства линейности для независимых
компонент.

Для заданного случайного вектора
компоненты уже независимы, следовательно,
мы можем найти дисперсию так:

Из ранее найденного имеем:

Тогда можно вычислить
.

Аналогично, имеем для дисперсии Y:

.

Вычислим матрицу ковариации

,

Надо вычислить ковариации новых компонент
вектора.

.

для наших независимых компонент равно
0.

Отсюда, матрица ковариации в явном виде:

.

Записываем плотность нового случайного
вектора

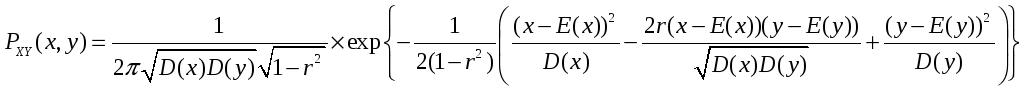
где
.

Подставив все значения, получим:

.

Для проверки распределения составим
матрицу квадратичной формы,

Возведем ее в (-1)-ую степень,
получили матрицу ковариации, что
показывает верность наших расчетов.

Содержание:

1. Случайные векторы
2. Свойства функции распределения случайного вектора
3. Двумерные дискретные случайные векторы
4. Двумерные абсолютно непрерывные случайные векторы
5. Сходимость случайных величин

Случайные векторы

Рассматриваем случайное явление и вероятностное пространство, которое отвечает этому случайному явлению. Пусть  – случайные величины, связанные с этим случайным явлением. Совместное распределение этих случайных величин будем называть случайным вектором и обозначать
Определение. Функцией распределения случайного вектора  называется функция n переменных

Свойства функции распределения случайного вектора

1. Функция распределения непрерывна слева и монотонно неубывающая по всем аргументам.
2. 
3. 
4. 
5. Функция распределения компоненты  является границей функции распределения случайного вектора для всех 
Определение. Случайный вектор  называется дискретным, если он приобретает конечное или счетное количество значений.
Очевидно, что каждая компонента этого случайного вектора является дискретной случайной величиной.
Дискретный случайный вектор определяется значениями, которые он приобретает, и вероятностями, с которыми приобретаются эти значения.
Далее будем считать, что компонента ξ₁ приобретает значения  компонента ξ₁ –  компонента ξ_n –  а

Определение. Случайный вектор  называется абсолютно непрерывным, если существует n-мерная действительная функция  которую мы будем называть плотностью абсолютно непрерывного случайного вектора  такая, для которой выполняется равенство

Определение. Компоненты случайного вектора  называются независимыми, если  выполняется равенство


Если случайный вектор является дискретным, то условие независимости конкретизируется так:


Для абсолютно непрерывного случайного вектора условие независимости является таким:

Пусть  – некоторая функция. Математическое ожидание случайной величины  равно


Если случайный вектор является дискретным и

если вектор ξ – абсолютно непрерывный.
Определение. Ковариантной матрицей случайного вектора  называют числовую матрицу К размера  вида

где

и если  то величина  называется ковариацией.
Понятно, что на диагоналях стоят дисперсии соответствующих компонент.
Легко видеть, что

Доказательство.




Коэффициентом корреляции компонент  является число

корреляционной матрицей является матрица

Детальнее свойства случайных векторов рассмотрим для двумерного случая.

Двумерные дискретные случайные векторы

Рассматриваем двумерный случайный вектор  Предположим, что компонента ξ приобретает значения компонента η приобретает значения  и  Распределение двумерного дискретного вектора удобно представлять в виде таблицы:

Очевидно, что 
где 
Пример. Дано распределение двумерного случайного вектора 

Найти
Решение. Поскольку

то 




Пример. Дано распределение двумерного случайного вектора 

Найти 
Решение. Очевидно, что



Распределение компонент находится так:

Далее определяем  
Пример. Дано распределение двумерного случайного вектора 

Найти распределение компонент.
Решение. 






Для контроля целесообразно сделать проверку. Известно, что  Убедимся, что это действительно так.

Следовательно, распределение компоненты ξ является таким:

Переходим к компоненте η:








Проверка: 
Следовательно, распределение компоненты η является таким:

Заметим, что распределение компонент можно находить значительно проще.
Запишем еще раз распределение вектора, добавив одну строку снизу и один столбец справа. Далее находим суммы элементов по строкам и записываем эти суммы в последний столбец, а также находим суммы элементов по столбцах и значения найденных сумм записываем в нижнюю строку. Полученные суммы являются значениями вероятностей. Например, сумма верхней строки является вероятностью сумма второй строки является вероятностью соответственно сумма третьей строки – Для того, чтобы найти  нужно найти сумму элементов второго столбца и т. д.

Определение. Условным распределением компоненты ξ при условии, что  называют совокупность значений

Аналогично, условным распределением компоненты η при условии, что называют совокупность значений

Условным математическим ожиданием компоненты ξ при условии, что  называют число

Аналогично, условным математическим ожиданием компоненты η при условии, что называют число

Пример. Дано распределение дискретного случайного вектора 

Найти условное распределение компоненты ξ при условии, что условное распределение компоненты η при условии, что  условное математическое ожидание компоненты ξ при условии, что условное математическое ожидание компоненты η при условии, что 
Решение. 
Значение вероятности  находим как сумму элементов второго справа столбца.

Далее



Следовательно, условное распределение компоненты ξ при условии, что  будет таким:

Сразу находим условное математическое ожидание компоненты ξ при условии, что 


Переходим к нахождения условного распределения компоненты η при условии, что 


Запишем это условное распределение в виде таблицы

Далее найдем условное математическое ожидание.


Условие независимости для двумерного дискретного случайного вектора является такой:

для произвольных 
Пример. Дано распределение двумерного случайного вектора 

Проверить, являются ли независимыми компоненты этого вектора.
Решение.   

Очевидно, условие  не выполняется. ■
Функция распределения для двумерного случайного вектора находится так. По определению имеем

Очевидно, что функция распределения является кусочно-постоянной на отрезках  Поэтому ее можно представить в виде таблицы, которая содержит на одну строку больше чем таблица распределения этого случайного вектора и на один столбец больше чем таблица распределения этого случайного вектора.
Поскольку случайный вектор  не содержит значений меньших, чем и , то элементы в крайнем левом столбце и верхней строке будут нулевыми. Далее алгоритм заполнения таблицы будет таким: в строке и столбце будет записана сумма вероятностей, которые отвечают
Пример. Дано распределение двумерного случайного вектора .

Найти функцию распределения.
Решение. Поскольку наименьшим значением среди  является 2, а среди является — 1, то вероятность того, что случайный вектор будет приобретать меньшие значения, равно 0. Поэтому слева и сверху мы проставляем нули.
Осталось заполнить 4 строки и 3 столбца. Обозначим значения незаполненных клеточек через  Очевидно, что


Пусть – некоторая кусочно-непрерывная функция. Математическое ожидание случайной функции находится так:

В частности ковариация находится по формуле

де



Коэффициент корреляции

Пример. Найти ковариацию и коэффициент корреляции случайного вектора 

Решение. Сначала найдем распределение компонент.


Далее находим   





И, наконец, находим


Переходим к коэффициенту корреляции.






Запишем ковариационную и корреляционную матрицы

Заметим, что если компоненты случайного вектора является независимыми, то ковариация, а следовательно, и коэффициент корреляции равняются нулю. Наоборот не всегда правильно.
Пример случайного вектора, у которого ковариация равна нулю и коэффициенты зависимы.

Сначала покажем, что ковариация равно нулю.





Далее проверяем компоненты на независимость


Следовательно,  а поэтому компоненты являются зависимыми. ■
Заметим, что если ковариация является ненулевой, то компоненты зависимы.

Двумерные абсолютно непрерывные случайные векторы

Рассматриваем двумерный абсолютно непрерывный вектор  с плотностью Плотность компонент находят так:

Пример. Плотность двумерного случайного вектора равна

где область D ограничена линиями    Найти плотность компонент.
Решение. Сначала изобразим область D.







Вероятность попадания в область  находится из формулы

Очевидно, что 
Пример. Дана плотность абсолютно непрерывного случайного вектора 

Найти      если область D ограничена линиями   
Решение. Сначала найдем неизвестную константу Для этого графически изобразим область D









Сначала найдем  Снова графически изобразим область






Далее находим вероятность  Изобразим графически область







Переходим к нахождению вероятности  Как и в предыдущих случаях сначала изображаем графически область интегрирования






И, наконец находим вероятность Изображаем графически область интегрирования

Как видно из рисунка, сначала нужно найти точку пересечения прямых  









Условие независимости компонент проверяется так:

Пример. Дана плотность случайного вектора 

где область D ограничена линиями     Найти и проверить, являются ли компоненты независимыми.
Решение. Прежде всего изобразим область D.







Следовательно,

Проверяем независимость компонент. Для этого находим их плотности



Следовательно,

Переходим к нахождению плотности η




Находим произведение  в области D и проверяем, равно ли оно


В области D имеем
Следовательно, условие независимости не выполняется. ■
Пример. Известно, что компоненты случайного вектора является независимыми. Их плотности равняются:
 
Найти совместную плотность случайного вектора .
Решение. Из условия независимости 
Поэтому

где область D ограничена линиями    
Функция распределения находится по определению

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти функцию распределения, если область D ограничена линиями    
Решение. Прежде всего находим неизвестную константу.





По определению имеем

Аналитический вид функции распределения зависит от того, где находится точка
В частности:
1. Пусть  или 
 
Тогда, как видно из рисунка

2.

Тогда





3. Далее рассмотрим точки для которых выполняются условия  

Очевидно аналитический вид функции распределения в этом случае будет таким:


4. Далее рассматриваем множество точек для которых выполняются условия  



5. Наконец, если   тогда



Условная плотность  находится по формуле

соответственно, условная плотность 

Пример. Дана плотность абсолютно непрерывного случайного вектора 

Найти неизвестную константу  условные плотности   если область D ограничена линиями   
Решение. Сначала изображаем область D и находим неизвестную постоянную.









Далее находим распределение составляющих











Следовательно, условия плотности будут такими:


Математическое ожидание от функции компонент вектора  равно

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти ковариацию, коэффициент корреляции, ковариационную матрицу, корреляционную матрицу, если область D ограничена линиями    
Решение. Сначала находим неизвестную константу 






Переходим к ковариации













Следовательно,


Далее находим дисперсии











Ковариационная матрица является такой:

Корреляционная матрица имеет вид

Сходимость случайных величин

Определение. Рассматриваем последовательность случайных величин Эта последовательность совпадает со случайной величиной ξ, если 

или

и это обозначают 
Определение. Последовательность случайных величин сходится к случайной величине ξ в среднеквадратичном, если   и

Это обозначают 
Теорема. Если  и  – непрерывная функция, то 

Закон больших чисел
Рассматриваем последовательность случайных величин  Для нее выполняется закон больших чисел (ЗБЧ) или эта последовательность удовлетворяет закон больших чисел, если

Сходимость по вероятности всегда проверять нет смысла, потому что есть теоремы, которые являются достаточными условиями для выполнения закона больших чисел.

Теорема Чебышева. Пусть дана последовательность независимых случайных величин  для которых существуют Если существует константа С такая, что   то для этой последовательности выполняется закон больших чисел.

Теорема Хинчина. Пусть дана последовательность независимых одинаково распределенных случайных величин  для которых существует математическое ожидание тогда для этой последовательности выполняется закон больших чисел.

Теорема Маркова. Пусть дана последовательность произвольных случайных величин  для которых существуют  и выполняется равенство

Тогда для этой последовательности выполняется закон больших чисел.

Теорема Бернулли. В схеме независимых испытаний Тут μ – относительная частота появления события, р – вероятность появления события в одном испытании.

Пример. Дана последовательность независимых случайных величин 

Проверить, выполняется ли для этой последовательности закон больших чисел.
Решение. Для проверки используем теорему Чебышева. Независимость дана в условии.



Очевидно, что

Поэтому для данной последовательности выполняются условия теоремы Чебышева, а следовательно, выполняется закон больших чисел. ■
Пример. Дана последовательность независимых случайных величин, которые имеют распределение Коши. Проверить, выполняется ли для этой последовательности закон больших чисел .
Решение. Поскольку для распределения Коши не существует математического ожидания, то речь не идет о выполнении закона больших чисел. ■