Вектор невязки как найти

Простой пример. Система

a+b=3
a-b=1

Вы используете какой-то приближённый метод и находите приближённое решение a=1,9 и b=1,2. Находите свободные члены, какими они были бы, если бы это решение было точным. Иными словами, находим систему уравнений, для которой полученные решения будут точными.

a+b = 1,9+1,2 = 3,1
a-b = 1,9-1,2 = 0,7

Невязки равны: 3 – 3,1 = -0,1; 1 – 0,7 = 0,3.

Теперь мы решаем то же самое уравнение, только вместо свободных членов ставим невязки

a+b=-0,1
a-b=0,3

Получаем решение a=0,1; b=-0,2. Для простоты я рассматриваю случай, когда на втором шагу алгоритма получается точное решение. Хотя этот процесс может быть бесконечным, и на каждом новом шагу мы получаем поправку к предыдущему решению.

Получаем:
a0 = 1,9; a1 = 0,1; a = a0 + a1 + … = 1,9 + 0,1 + … = 2;
b0 = 1,2; b1 = -0,2; b = b0 + b1 + … = 1,2 – 0,2 + … = 1.

Некоторые вычислительные особенности слау

Погрешности и
невязки

Для
оценки точности найденного решения
СЛАУ существует две общеупотребительной
меры погрешности:

1. вектор
   ошибок
   

где
точное решение

-найденное
решение

Мера абсолютно точная, только для того,
чтобы ею пользоваться нужно

Чтобы избежать трудностей, вводят другую
меру

1. вектор
   невязок
   

Невязка
– количественная мера несоответствия
между правыми и левыми частями системы
уравнений при подстановки в них
вычислительного решения.

Очевидно,
что равенство нулю вектора ошибок влечет
за собой равенство нулю вектора невязок.

Однако,
в общем случае из малости величины
невязок не следует малость ошибки. Т.е.
несмотря на то, что найденное решение
почти удовлетворяет уравнению, оно
может совсем не подходить в качестве
подлинного решения. Невязка полезна в
том смысле, что с ее помощью можно
осуществить контроль точности решения.
Т.к. использовать в качестве меры контроля
вектор ошибок не представляется возможным
в виду того, что неизвестно точное
решение.

Пример.
Рассмотрим систему

Предположим,
что мы провели вычисления (неважно каким
методом) и нашли решение

Если
вычислить невязки, то невязки будут
равны

Для
погрешность
10^-2, но точное решение

В
общем случае можно утверждать, что для
оценки величины невязки и погрешности
можно использовать следующие формулы:

Число
называется числом обусловленности
матрицы А и математически оно показывает,
насколько матрица системы А близка к
вырожденной или иными словами, числомера вырождения матрицы А, а именно, чем
выше,
тем ближе матрица к вырождению.

Обусловленность-
это внутреннее свойство матрицы СЛАУ.
Оно не связано с каким либо численным
методом. В общем случае, можно утверждать,
что матрица с большим числом обусловленности
дает большие ошибки при решении СЛАУ.

Математически
точно число обусловленности можно
вычислить.

Введем
число
;

Тогда
число обусловленности представляет
собой:

Тогда мы можем утверждать, что погрешность
решения:

Вычислительная
эффективность правила Крамера

Правило
Крамера широко применяется для нахождения
решения СЛУ

Если
сосчитать количество операций, которых
нам надо сделать

n	3	10	20
N	17	3.6*107	5*1019
t

Численные методы
решения СЛАУ

Все
численные методы решения СЛАУ принято
делить на два класса:

1. прямые

2. итерационные

Прямые
методы используют некоторые формулы
для вычисления неизвестных величин за
конечное число шагов вычислительного
процесса

Пример.
Метод обратной матрицы

Существенным
недостатком прямых методов является
необходимость хранения в памяти
компьютера всех n- квадратных элементов
матрицы системы, т.е прямые методы
никаким образом не учитывают разряженную
структуру матрицы в системы.

Кроме
этого применения прямых методов для
решения СЛАУ с большим числом переменных
приводит к значительному накоплению
вычислительных погрешностей.

К
широко известным методам относится
метод Гаусса, метод прогонки.

Итерационные
методы ( методы последовательных
приближений)-это методы, в которых с
помощью какого- либо алгоритма строится
цепочка приближенных решений

Каждый
цикл таких вычислений называется
итерацией.

Итерационные
алгоритмы сложнее прямых методов. Объем
необходимых вычислений при их использовании
заранее трудно определить, но они не
требуеют при работе с разряженными
матрицами хранение всех ее элементов.
Более того, зачастую в них используются
вычислительные формулы, задающие эти
примеры. Итерационный процесс устроен
таким образом, что вычислительные ошибки
от итерации к итерации не накапливаются.
Поэтому итерационный метод можно
использовать как для решения хорошо
обусловленных так и плохообусловленных
СЛАУ.

Примеры:
Метод простой итерации и метод Гаусса-
Зейделя

Метод исключения
Гаусса

Хорошо
известно, что алгоритм метода Гаусса
для решения СЛАУ состоит из двух основных
шагов.

1. На
   прямом ходе путем последовательного
   исключения переменных из уравнений
   системы, матрицу системы приводят к
   треугольному виду.

решение методом исключения дает
верхнетреугольную матрицу:

1. На
   обратном ходе вычисляется точное
   решение системы

подставляем в предыдущее уравнение и
получаем:

Метод
Гаусса применим эффективно лишь в том
случае, когда матрица системы хорошо
обусловлена, имеет низкое число
обусловленности.

Точность
вычисления значительно зависит от
способа нахождения ведущего элемента,
который мы используем, для исключения
переменных на прямом ходе.

Пример.Рассмотрим систему:

Возьмем
в качестве ведущего элемента

При
решении получим:

если округлить, то примерно получим,
что неправильно!

Теперь,
возьмем в качестве ведущего элемента
коэффициент перед
из второго уравнения, т.е 1.

Тогда,
если округлить, то получим правильное
решение

Правила
для выбора ведущего элемента:

1. выбор
   по столбцам

Рассматривается первый столбец.
Предполагается, что мы хотим исключить
.
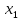
Находим в этом столбце максимальный
элемент, т.е.
Находим уравнение, где коэффициент присамый большой и переставляем это
уравнение на первое место и используем
коэффициент прив качестве ведущего элемента.

1. выбор
   по строке

Из первого уравнения находим переменную,
которую будем исключать. Ищем
и ищем соответственно,
которое соответствует этому максимальному
элементу. И ставимна первое место и исключаем его.

Эту методику можно обобщить на все
элементы

1. по
   всей матрице

Сканируем столбцы и строчки и ищем
.
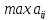
Находим,
и ставим этот элемент на первое место
.

Этот прием наиболее приемлем.

Метод прогонки

Метод
прогонки является частным случаем
метода Гаусса, который специально
предназначен для решения систем уравнений
с разряженной диагональной матрицей

1. Прямой
   ход состоит в том, что вычисляются
   коэффициенты

Сам процесс состоит в следующем.

1. Обратная
   прогонка соответствует вычислению
   переменных в обратном порядке, начиная
   с самого последнего x

зная
,
можно найти

Итерационные
методы

В общем случае схема итерационных
методов решения СЛАУ заключается в
следующем:

1. каким-
   либо посторонним способом нужно
   установить, какое- либо начальное
   решение
   

2. вычисляем
   правую часть:
   

3. находим
   невязку:
   

4. находим
   решение системы уравнений:
   ,–
   вектор поправок

5. 

6. из 5.
   пункта идем во 2.

Важным
вопросом является, когда нужно
остановиться!

В
качестве остановки используют какое-
либо векторное неравенство, которое
сравнивает решения, полученные на
предыдущей и последующей итерации.

Введем
норму:

Соседние файлы в папке ммм

• #
• #

  11.03.20169 б13Desktop__.ini

• #
• #
• #
• #
• #

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 января 2021 года; проверки требуют 4 правки.

Невязка — величина ошибки (расхождения) приближённого равенства.

Пусть требуется найти такое x, что значение функции:

Подставив приближенное значение x₀ вместо x, получаем невязку

а ошибка в этом случае равна

.

Если точное значение x неизвестно, вычисление ошибки невозможно, однако при этом может быть определена невязка.

Невязка аппроксимации функции[править | править код]

Схожее название используется в дифференциальных,
интегральных и
функциональных уравнениях.

Для аппроксимации
решения
уравнения

,

невязка может быть функцией

или по-другому максимумом нормы разности

на области , где функция

есть усреднённое решение ,
или некоторый интеграл функции разности, например,

В большинстве случаев, чем меньше невязка, тем аппроксимированное значение ближе к решению, то есть,

В этом случае начальное уравнение принималось за корректное; и невязка могла быть использована как показатель отклонения аппроксимации от точного решения.

Использование невязок[править | править код]

Если точное решение неизвестно, можно использовать аппроксимацию решения с небольшой невязкой.

Невязка фигурирует во многих разделах математики, в том числе в итерационных методах, таких как метод обобщенного минимума, в котором решение системы уравнений находится путём минимизации невязки.

В навигации невязкой называется расстояние между вычисленным по прокладке местоположением судна и фактически определённым (по светилам, маякам и т.д.) местоположением, измеряется в морских милях.

Вектор – невязка

Cтраница 3

В алгоритме метода Ньютона, согласно итерационной формуле (8.36), матрица А представляет собой матрицу Якоби решаемой системы алгебраических уравнений F ( X) 0, а вектор В – вектор невязок уравнений этой системы.
 [31]

Матрица Гх в этом случае будет представлять собой корреляционную матрицу оценки параметров по предыдущим п измерениям, и вследствие того, что имеется лишь одно новое измерение, весовая матрица W и вектор невязок dz превратятся в скаляры.
 [32]

Аналогичным образом система ( 4 – 12) превратится в систему ( 4 – 10), если предположить, что на всем интервале времени вектор Z ( t), называемый вектором невязки, тождественно равен нулю.
 [33]

Для обеспечения сходимости вычислительного процесса автором разработан метод анализа и управления сходимостью. Анализ производился по норме вектора невязок ДД а управление заключается в переключении вычислений с одного метода на другой и переопределении фундаментальных циклов по принципу минимизации длины дерева.
 [34]

На рис. 8.18 – 8.24 сравниваются результаты, полученные при различных итерационных методах для описанных семи задач. На этих рисунках IIRIU – / – норма вектора невязки, поделенная на сумму источников, а п – эквивалентное число LSOR-итераций, подсчитанное с помощью коэффициентов вычислительных затрат, приведенных в табл. 8.1. Результаты для каждой задачи подытожены ниже.
 [35]

Очевидно, что необходимо определять оптимальное число полиномов в разложении, причем оно существенно зависит от величины экспериментальной ошибки. Критерий, использованный в работах [262, 282, 332, 366] ( минимизация нормы вектора невязки), такими свойствами не обладает.
 [36]

На некоторых вычислительных машинах следует использовать процедуры точного вычисления скалярного произведения только для векторов невязок.
 [37]

В любом случае предпочтительнее использовать условие окончания итерационного процесса (8.15), ограничивающее норму вектора невязок, так как оно в известной мере определяет точность полученного решения.
 [38]

Функция line полностью дублирует возможности функций slope и intercept, но более удобна в практическом применении. Эти функции реализуют метод наименьших квадратов, в качестве критерия которого выступает скалярное произведение вектора невязок системы линейных алгебраических уравнений, образованной отдельными уравнениями прямой для каждой пары согласованных значений х л у ( см. разд.
 [39]

Значительное различие величин фазовых переменных приводит к плохой обусловленности системы алгебраических уравнений и существенно затрудняет получение их решения с необходимой точностью. С целью улучшения обусловленности уравнений и повышения сходимости итерационного процесса необходимо вводить нормирование вектора фазовых переменных и вектора невязок.
 [40]

Соотношением для получения новых значений итерируемых переменных все время остается формула (11.20), в которой происходят соответствующие модификации матриц D и X. Причем при введении в них информации о новой точке у матрицы D появляется новая строка, соответствующая вектору невязок уравнений (11.14) на данном шаге итерации, и новый столбец, соответствующий введению нового члена в (11.17), а у матрицы X заполняется только новая строка, в которой будут храниться координаты новой точки. Если в процессе такой коррекции та или иная переменная прижимается к своей границе, то это, как правило, свидетельствует о некорректном задании этой границы.
 [41]

В процедурах unsym асе solve и сх асе solve необходимо запоминать исходные матрицы А и В. Результат разложения матрицы А на две треугольные располсн жен в массиве аа, а в массиве ЪЪ – последовательности векторов невязок и поправок. Вычисление точного скалярного произведения необходимо при нахождении невязок. Если накопление скалярного произведения или вычисление с двойной точностью по какой-либо причине нецелесообразно, то вычисление скалярного произведения производят с обычной точностью, за исключением случая, когда необходимо определить невязку решения.
 [42]

В системе ПИОНЕР реализован целый набор методов оптимизации невыпуклых недифференцируемых функций. Получаемые решения, как правило, являются приближенными, причем на любом этапе счета имеется возможность получения числового значения вектора невязок ( для задач с ограничениями), предусмотрены также различные способы оценки точности вычисления целевой функции. В настоящее время система находится в процессе эксплуатации.
 [43]

Наряду с алгоритмом least squares solution в Справочнике приведены алгоритмы, которые используют ортогональные преобразования исходной матрицы А к треугольной форме, опираясь на процедуру ортогонализации Грама-Шмидта. При этом вычисляют ортогональный базис пространства, порожденного столбцами матрицы А, и каждый вектор правых частей b выражают через этот базис и вектор невязки г, ортогональный ему.
 [44]

Главная, возможно даже единственная, слабость обратной итерации-это то, что вычисленные векторы для двух близких собственных значений могут быть приемлемы ( по критерию малости их невязок) и все же не быть взаимно ортогональными. Это звучит как противоречие, поскольку точные собственные векторы должны быть ортогональны. Однако малый вектор невязки rk гарантирует точность лишь в случае изолированных собственных значений, как показывают теоремы гл.
 [45]

Страницы:  

   1

   2

   3

   4
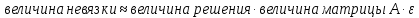
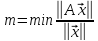
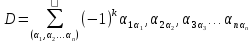
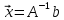
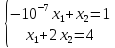
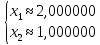