Вектор сдвига линейного многообразия как найти

Понятие линейного многообразия Способы задания линейного многообразия Свойства линейного многообразия Размерность линейного многообразия Арифметические операции над линейными многообразиями

Понятие
линейного многообразия

При
рассмотрении примеров линейных
подпространств, было указано, что в
геометрическом пространстве

векторов пространства каждая прямая и
каждая плоскость, проходящие через
начало координат, определяют линейное
подпространство. Прямым и плоскостям,
не проходящим через начало координат,
соответствует в линейной алгебре новый
математический объект – линейное
многообразие.

Пусть

– линейное пространство,

– некоторое его подпространство,
содержащее векторы
,
(9)

–
некоторый вектор из пространства

.
Все векторы считаются отложенными от
начала координат. Множество

всевозможных векторов вида

,
где вектор

есть любой вектор из множества векторов
(9) или любая их линейная комбинация,
называется линейным
многообразием
и обозначается

.
Линейное многообразие, очевидно, получено
сдвигом подпространства

на вектор

(рис. 4.5). Вектор

называется вектором
сдвига,
подпространство

–
направляющим подпространством
линейного многообразия

.

Линейное
многообразие

обращается в линейное подпространство

,
когда вектор сдвига

.

Пусть
линейное подпространство

– это совокупность всех векторов, лежащих
на прямой, которая проходит через начало
координат (рис. 4.5). Положим один из этих
векторов равным

.
И пусть вектор

.
Тогда линейное многообразие

состоит из множества векторов

,

,
концы которых лежат на прямой, полученной
сдвигом исходной прямой на вектор

.

Способы
задания линейных многообразий

Линейное
многообразие может быть задано с помощью
векторов следующим образом: задается
базис векторного подпространства

и вектор сдвига

.

Другой
способ задания – посредством системы
неоднородных линейных уравнений.
Множество решений неоднородной системы
линейных уравнений является линей­ным
многообразием. Обоснуем это утверждение.
Напомним, что общее решение системы
линейных уравнений

склады­вается из общего решения
однородной системы

и базисного (частного) решения неодно­родной
системы

.
Общее решение однородной системы есть
линейная комбинация фундамен­таль­ного
набора решений (ФНР), задающего некоторое
линейное подпространство

.
Линейная комбинация ФНР плюс базисное
решение есть общее решение системы
неоднородных линейных уравнений. Поэтому
линейное многообразие можно представить
как множество решений некоторой в общем
случае неоднородной системы линейных
уравнений

.

Свойства
линейного многообразия.

1. Вектор
   сдвига

   принадлежит линейному многообразию.

◄Линейное
подпространство содержит нулевой
вектор:

.
Поэтому в суммах векторов

содержится вектор

.►

1. Вектором
   сдвига, принадлежащим линейному
   многообразию, может быть любой вектор
   этого линейного многообразия.

◄Пусть

.
Возьмем произвольный вектор

.
Тогда существует вектор

такой, что

,
причем

.
Найдем сумму подпространства

и вектора

.

.

Получим
то же линейное многообразие

.►

1. Линейное
   многообразие

   определяется однозначно
   по известным подпространству

   и вектору сдвига

   .

◄Предположим,
что существует еще одно линейное
многообразие

,
построенное на линейном подпространстве

,
сдвинутом на вектор

.
Выберем базис

в подпространстве

.
Любой вектор

из линейного многообразия

может быть представлен в виде линейной
комбинации векторов базиса линейного
подпространства

и вектора сдвига

.

Точно
также, в виде линейной комбинации можно
представить любой вектор

из линейного многообразия

:
,

где

.
Но тогда вектор

,
а вектор

.
Векторы

и

– это произвольные векторы из линейных
многообразий

и

.
Следовательно,

=
.►

Размерность
линейного многообразия

Определение.
Размерностью
(рангом)
линейного многообразия

называется размерность линейного
подпространства

:

Если
линейное подпространство

состоит только из нулевого вектора, то

.
Такое линейное многообразие имеет
размерность

,
называется 0-мерным линейным много­образием
(ранг равен нулю) и геометрически
соответствует точке (конец единственного
вектора

).

Если
линейное подпространство


,
т.е.
состоит из векторов, лежащих на одной
прямой, то линейное многообразие

называется одномерным. Его ранг равен
единице. Геометрическая интерпре­тация
многообразия – прямая (концы всех
векторов лежат на прямой), не проходящая
через начало координат.

Линейное
многообразие, полученное из подпространства,
состоящего из векторов плоскости,
называется двумерным. Его геометрический
образ – плоскость.

В

–мерном векторном пространстве линейное
многообразие размерности

называется гиперплоскостью,
а размерности
,
где
,
– k-мерной
плоскостью.

Подобно
прямым или плоскостям линейные
многообразия могут пересекаться,
скрещиваться, быть параллельными.
Вводится также операция проектирования
одного линейного многообразия на другое.
Об этом подробнее в (9).

Операции
с линейными многообразиями и их взаимное
расположение.

1. Сумма
   двух линейных многообразий
   

   и
   

   есть линейное много­образие,
   определяемое по следующему правилу:

.

В
частном случае при

имеем

1. Пересечение
   двух линейных многообразий

   и

   есть линейное многообразие, вычисляемое
   по правилу

,

где

.

1. Умножение
   линейного многообразия
   

   на число
   

   порождает новое линейное многообразие
   
   ,
   определяемое так:

.

1. Параллельность
   двух линейных многообразий

   и

   означает, что направляющее подпространство
   одного из них содержит направляющее
   подпространство другого:

,
если

или

.

1. Скрещивание
   двух
   линейных многообразий

   и

   имеет место в том случае, если они не
   пересекаются и не параллельны.

ПРИМЕР
1. Линейное многообразие

задано системой линейных уравнений

Найти
линейное подпространство

и вектор сдвига

такие, что

.

Решение.
Составим расширенную матрицу из
коэффициентов и свободных членов системы
уравнений и преобразуем ее, используя
метод Гаусса.


.

Вернемся
к системе уравнений, взяв свободными
переменными

.

Выделим фундаментальный
набор решений (ФНР)

.

Линейно
независимые векторы

составляют ФНР, а, следовательно, базис
подпространства

.
Любой вектор

можно представить в виде

.
Вектор сдвига есть вектор

.

ПРИМЕР
2. Линейное многообразие

имеет вид

,
где

,

,

,

.

Представить линейное
многообразие в виде системы линейных
уравнений.

Решение.
Линейное многообразие

есть множество векторов вида

или в координатном виде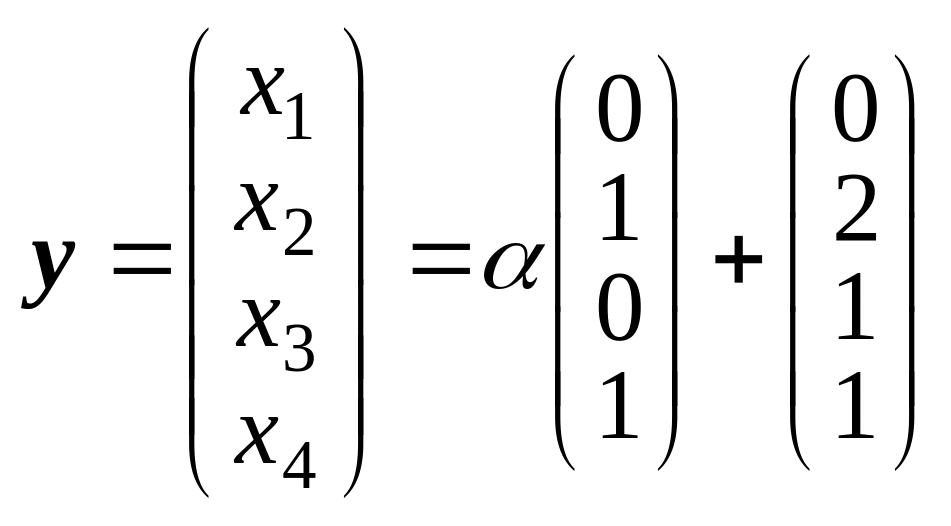
.

Перепишем
систему уравнений относительно переменной

,
выделив столбец свободных членов.

.

Представим систему
матрицей коэффициентов и воспользуемся
методом Гаусса



.

Система совместна
при условии, что ранг матрицы коэффициентов
равен рангу расширенной матрицы (теорема
Кронекера-Капелли).

Следовательно,

или

Линейное
многообразие

записано в виде системы неоднородных
линейных уравнений.

Рассмотрим
вопросы взаимного расположения линейных
многообразий. Начнем с простого примера.

ПРИМЕР
3. Пусть в трехмерном линейном векторном
пространстве заданы два двухмерных
многообразия

где

и

,
где

Найти
пересечение линейных многообразий
.

Решение.
Произвольный вектор
,
принадлежащий
как одному так и другому линейному
многообразию, может быть представлен
в виде

(10)

или

,

где

– координаты вектора


в базисах направляющих подпространств
линейных многообразий. Для удобства
перепишем матричное уравнение так

Чтобы
найти
,
составим расширенную матрицу и
преобразуем ее методом Гаусса-Жордана

,

откуда
следует
.
Подставив

в равенство (10), получим

.

Следовательно,
две двухмерные плоскости пересекаются
по прямой (
).
Такой вывод можно сделать по виду
преобразованной методом Гаусса-Жордана
расширенной матрицы. Во второй строке
2-го и 3-го столбцов матрицы стоят отличные
от нуля цифры. Значит, существует только
одна независимая переменная, например,

.
ФНР содержит одно решение (один вектор).
Этот вектор составляет базис подпространства
размерности один, являющегося пересечением
направляющих подпространств линейных
многообразий.

Возможны
другие варианты решений для двух
плоскостей в трехмерном пространстве.

Пусть
преобразованная матрица имеет вид

.

Значок

поставлен в позициях, содержащих любое
число. Если на пересечении последних
столбца и строки стоит единица, решений
нет (линейные многообразия не пересекаются

).
Кроме того, поскольку

зависят от
,
ФНР будет содержать два независимых
решения (два вектора). Они составят базис
двухмерного подпространства. При наличии
единицы в последней строке последнего
столбца двухмерные плоскости параллельны.

Если
на пересечении последних столбца и
строки стоит нуль, решения существуют
(двухмерные плоскости пересекаются по
плоскости, т.е. совпадают,
.

Замечание.
В преобразованной методом Гаусса-Жордана
матрице в некоторых позициях могут
стоять вместо единиц и нулей другие
числа. Метод исследования взаиморасположения
многообразий остается справедливым,
если выполнены два условия:

1. Ранг
   матрицы базиса направляющего
   подпространства линейного многообразия
   соответствует рангу матрицы, составленной
   из столбцов, у которых только в одной
   позиции по вертикали стоит единица.

2. Если
   все базисные векторы какого-либо
   подпространства, расположенные по
   столбцам, содержат нули в определенной
   строке, то соответствующая матрица с
   единицами только в одной позиции по
   вертикали должна содержать в этой
   строке нули.

ПРИМЕР
4. Рассмотреть все варианты взаимного
расположения трехмерного

и двумерного

многообразий в пятимерном пространстве.

Решение.
Перечислим существенно различные
варианты:

1)
,
2)

1а)
Комбинация цифр в последнем столбце
«
»
→
.
Многооб­ра­зия не имеют общих точек.

1б)
Комбинация «

»
→
.
Многообразие

включено в многообразие
.

2а)
Цифра в последнем столбце «1»
→
.
Многообразия не имеют общих точек.

2б)
Цифра в последнем столбце «0»
→

Многообразия пересекаются по прямой.

3)

,
многообразия пересекаются в точке.

4.4.
Метрические пространства

Аксиомы метрического пространства Нормы метрического пространства Геометрическая интерпретация норм

Аксиомы
метрического пространства

Векторное
пространство

называется
метрическим,
если задано некоторое правило, по
которому каждой паре векторов

ставится в соответствие некоторое число

.
Оно должно удовлетворять 3 аксиомам:

1.

для всех

и

при

.

2.

для всех

;

3.

для всех

.

Это
число

,
где

и

,
называется расстоянием
между векторами

или нормой,
а правило (функция двух векторов, формула)
– метрикой.
Метрику можно ввести по-разному. Докажем,
что векторное пространство

станет
метрическим, если для любых x
и y
из

положить

.

Покажем,
что выполняются аксиомы метрики.
Действительно, из свойств нормы вытекает,
что

1. 
   ,
   причем

   тогда
   и только тогда, когда
   
   .

2. 
   .

3. 

   
   .

Нормы
метрического пространства

Модуль
разности векторов может быть вычислен
в координатах по-разному (разные нормы).
В экономике наиболее распространены
следующие:

1. евклидова
   норма:
   .

В
частном случае расстояние между вектором

и нулевым вектором

есть норма вектора

=
.

1. октаэдрическая
   норма:
   
   .

Норма
вектора в векторном пространстве с
октаэдрической нормой есть величина

=
.

1. кубическая
   норма:
   
   .

Норма
вектора

вычисляется по формуле

=
.

Задавая
по-разному модуль разности векторов в
координатах, мы должны убедиться в том,
что аксиомы метрики не нарушены. Проверим
справедливость аксиом на примере
евклидовой нормы.

1. Очевидно
   
   ,
   причем

   при
   .

2. 
   3.
   Аксиома

   для метрики
   

   имеет вид

.

Пусть

и

.
Тогда получим неравенство

,

которое
называется неравенством
треугольника.
Докажем его.

Запишем
неравенство в координатной форме

.

Для
доказательства возведем обе части в
квадрат и раскроем скобки. После упрощения
получим неравенство в координатах,
называемое неравенством
Коши-Буняковского

.

Докажем
его справедливость. Рассмотрим очевидное
неравенство

,

г
де
параметр

.
Раскрыв скобки, приведем его к квадратному
неравенству относительно

.

.

Поскольку
неравенство выполняется при всех

,
его дискриминант не положителен (
)

,

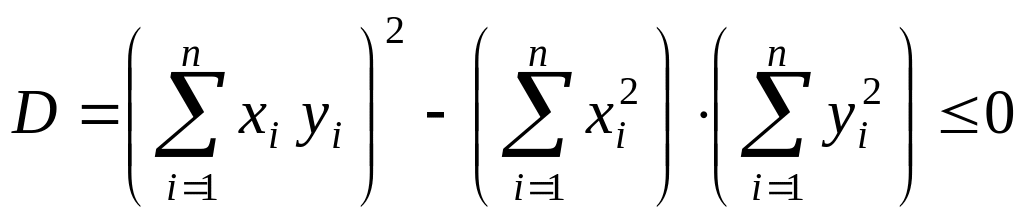
о
ткуда
получаем неравенство Коши-Буняковского.
Доказательство закончено.

Все
аксиомы проверены.

Геометрическая
интерпретация норм

Дадим
геометрическую интерпретацию каждой
нормы при

и

.

Для
евклидовой нормы величина

есть
расстояние между концами векторов

и

,
указанное пунктирной линией (рис. 4.6).
Эта величина соответствует расстоянию
между двумя точками на плоскости в нашем
физическом пространстве.

Октаэдрическая
норма устанавливает расстояние между
концами векторов

, (10)

п

оказанное
пунктирной линией на рис. 4.7. Наглядно
представить себе это расстояние можно
следующим образом. Представим себе, что
мы находимся в той части города, где
улицы пересекаются под прямыми углами
(рис. 4.8). Рас­сто­яние от А
до В
мы можем пройти, двигаясь по улицам, по
траектории АСВ
или, например, по траектории АDВ.
Но не мо­жем пройти по траектории АВ.
Для нас расстояние от точки А
до точки В
вычисляется по формуле (10).

Расстояние,
определяемое кубической нормой

,

представ­лено
на рис. 4.9 пунктирной линией. Дадим
экономи­ческую интер­пре­­та­цию
этой нормы. Если вы можете заработать

ден. единиц, но обязаны израсхо­довать

ден. единиц, или, заработав

ден. единиц, израсходуете при этом

ден. единиц, ваш потребительский выбор,
нацеленный на наибольшую выгоду, будет
таким: максимум из двух величин

или

.

ПРИМЕР.
Метрика линейного векторного пространства

задается правилом

.
На координатной плоскости изобразить
множество точек, для которых

,
если в метрическом пространстве принята
1. евклидова норма; 2. октаэдрическая
норма; 3. кубическая норма. Ограничиться
рассмотрением случая

.

Решение.
В двумерном векторном пространстве

с евклидовой нормой и

уравнение

имеет вид

или

,
с октаэдрической нормой –

,
с кубической нормой –

.
На координатной плоскости

построим
соответствующие графики (рис. 4.10)

Д
ля
понимания того, как выглядит объемное
тело, если расстояния измерять, пользуясь
разными нормами, введем понятие
математического шара в метрическом
пространстве. Математическим
шаром
с центром в точке

и радиусом

в трехмерном метрическом пространстве
назовем множество

.

В
метрическом евклидовом пространстве
это неравенство имеет вид

и
представляет собой знакомый нам
геометрический шар. Евклидова норма
при

описывает наше физическое трехмерное
пространство.

В
линейном векторном пространстве с
октаэдри­ческой нормой математический
шар

является
более сложной фигурой. Изобразим ее на
рис. 4.11, взяв центром точку

и радиусом

.
Это октаэдр (восьмигранник). Поэтому и
норма названа октаэдрической.

Математический
шар в линейном векторном пространстве
с кубической нормой

представляет
собой куб, отсюда название нормы.

Линейные многообразия: определение и примеры

Определение линейного многообразия

Пусть подпространство линейного пространства , а — некоторый вектор. Множество векторов , представимых в виде , где , называется линейным многообразием, проходящим через вектор параллельно подпространству , и обозначается

Говорят также, что линейное многообразие получено параллельным сдвигом подпространства на вектор , а подпространство называют однородной частью линейного многообразия . Размерностью линейного многообразия называют размерность его однородной части, т.е. . B n-мерном линейном пространстве (n-l)-мерное линейное многообразие называется гиперплоскостью. Обратим внимание на то, что раз мерность многообразия равна максимальному числу линейно независимых векторов не самого многообразия, а его однородной части.

---

Примеры линейных многообразий

1. Любое подпространство является линейным многообразием , где — нулевой вектор.

2. В пространстве (радиус-векторов с общим началом в точке ) рассмотрим плоскость , проходящую через точку (рис.8.3) и плоскость , проходящую через конец вектора параллельно плоскости .

Любой вектор , конец которого принадлежит плоскости , можно пред ставить в виде , где — вектор, принадлежащий плоскости . Следовательно, множество радиус-векторов, концы которых принадлежат плоскости , это линейное многообразие . Его размерность равна 2, так как (базисом являются любые два неколлинеарных вектора, принадлежащие , например, векторы и ). Заметим, что вектор в многообразии можно заменить любым радиус-вектором , конец которого принадлежит плоскости , т.е. .

---

Свойства линейных многообразий

1. Линейное многообразие, параллельное линейному подпространству , однозначно определяется любым своим вектором, другими словами, если , то .

2. Непустое пересечение линейных многообразий является линейным многообразием, другими словами, если , то , т.е. однородная часть пересечения совпадает с пересечением однородных частей многообразий, а вектор, определяющий сдвиг — это любой вектор пересечения многообразий.

3. Любое r-мерное линейное многообразие можно представить как аффинную оболочку не более, чем векторов.

В самом деле, пусть — r-мерное линейное многообразие, т.е. . Выберем базис подпространства и образуем векторов линейного многообразия . Покажем, что . Действительно, любой вектор можно представить в виде . Преобразуем это выражение, подставляя

Получили аффинную комбинацию векторов , так как сумма коэффициентов равна единице. Следовательно, .

Пусть теперь . Тогда , причем . Подставляя , получаем:

то есть . Следовательно, .

Из двух включений получаем равенство . Из доказательства следует, что

4. Аффинная оболочка непустого подмножества конечномерного пространства является линейным многообразием.

---

Взаимное расположение линейных многообразий

Линейные многообразия обобщают обычные объекты стереометрии -прямые и плоскости. Следующие признаки и определения обобщают известные стереометрические свойства, характеризующие взаимное расположение прямых и плоскостей. Геометрическая терминология естественно применяется для многообразий. Говорят, что одно линейное многообразие лежит в другом, если первое многообразие является подмножеством второго. Пересечение или объединение линейных многообразий понимается как пересечение или объединение множеств векторов. Говорят, что линейные многообразия не пересекаются, если у них нет общих векторов, т.е. пересечение этих множеств пусто.

Приведем признаки включения и равенства (совпадения) линейных многообразий:

1) линейное многообразие лежит в линейном многообразии тогда и только тогда, когда и ;

2) линейные многообразия и совпадают тогда и толь ко тогда, когда и .

Два непересекающихся линейных многообразия и называются параллельными, если одно из подпространств или лежит в другом: или (иными словами, если одна из однородных частей содержится в другой).

Два непересекающихся линейных многообразия и называются скрещивающимися, если пересечение подпространств и есть нулевой вектор: .

---

Способы описания линейных многообразий

Для линейных подпространств рассматривались два способа описания: внутренний (при помощи линейных оболочек) и внешний (при помощи однородной системы уравнений). Свойства 3, 4 определяют внутреннее описание линейных многообразий при помощи аффинных оболочек векторов. Внешнее описание линейных многообразий задается неоднородной системой линейных уравнений. Действительно, множество решений будем рассматривать как подмножество я -мерного арифметического пространства . Структура общего решения неоднородной системы:

где — частное решение неоднородной системы, — фундаментальная система решений соответствующей однородной системы — произвольные постоянные, — ранг матрицы системы. Как показано ранее, множество решений однородной системы является линейным подпространством , а именно . Следовательно, множество решений неоднородной системы является линейным многообразием в

В частности, множество решений одного уравнения с ненулевыми коэффициентами (хотя бы один коэффициент при неизвестных отличен от нуля), представляет собой гиперплоскость, т.е. линейное многообразие размерности , так как размерность его однородной части равна , поскольку . Поэтому множество решений системы линейных уравнений можно представить как пересечение гиперплоскостей. По свойству 2 пересечение линейных многообразий есть линейное многообразие.

Равенство (8.24) определяет переход от внешнего описания линейного многообразия (левая часть) к внутреннему описанию (правая часть). Рас смотрим обратный переход: от внутреннего описания к внешнему.

Пусть дано линейное многообразие . Требуется составить неоднородную систему уравнений, множество решений которой совпадало бы с заданным многообразием. Учитывая, что разность двух решений неоднородной системы является решением однородной системы, используем переход от внутреннего описания линейного подпространства к внешнему. Для нахождения неоднородной системы нужно выполнить следующие действия.

1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.

2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .

3. Из последних строк матрицы составить матрицу .

4. Записать искомую систему уравнений в форме .

---

Пример 8.14. Многообразие задано аффинной оболочкой векторов

где

Составить систему неоднородных уравнений, задающую это же многообразие.

Решение. Согласно (8.23), зададим линейное многообразие в форме .

1. Из данных столбцов составляем матрицу , а затем блочную матрицу

2. Элементарными преобразованиями над строками блочной матрицы и над ее первыми тремя столбцами приводим левый блок к простейшему виду. Прибавляем ко второй и последней строке первую, умноженную на (-1), затем меняем местами вторую и третью строки:

Прибавим ко второму и третьему столбцам первый, умноженный на (-1), а затем к третьему столбцу — второй, умноженный на (-2). При этом в левом блоке получим простейший вид матрицы (ее ранг ), а правый блок матрицы не изменится:

3. Из последних строк матрицы составляем матрицу

4. Записываем искомую систему уравнений в форме

---

Пример 8.15. Найти размерность пересечения многообразий и , если — многообразие, заданное в примере 8.14 аффинной оболочкой век торов, а многообразие — множество решений неоднородной системы

Решение. В примере 8.14 найдена система неоднородных уравнений, описывающая многообразие Составляя из систем и одну систему, получаем внешнее описание пересечения многообразий: . Найдем множество решений этой системы. Составляем матрицу системы и приводим ее к ступенчатому виду:

Система имеет единственное решение . Следовательно, пересечение многообразий состоит из одного вектора. Поскольку однороная часть пересечения представлена нулевым пространством, то .

---

Пример 8.16. Исследовать взаимное расположение многообразий и , если — многообразие, заданное в примере 8.14 аффинной оболочкой векторов, — многообразие, заданное в примере 8.15 неоднородной системой уравнений, а многообразие — проходит через вектор параллельно линейной оболочке вектора .

Решение. В примере 8.15 показано, что многообразия и пересекаются и , .

Найдем пересечения многообразия с многообразиями и . Любой вектор из имеет вид , где параметр . Подставим выражения для координат этого вектора в системы, описывающие многообразия и (система для многообразия получена в примере 8.14):

Каждая из систем несовместна. Следовательно, многообразие не пересекает многообразий и .

Найдем пересечение однородной части с однородными частями и . Однородная часть задана линейной оболочкой . Однородную часть находим по правилу (8.23):

Так как , то справедливо включение

Поскольку однородная часть многообразия содержится в однородной части многообразия , то, согласно определению, многообразия и параллельны.

Однородную часть определяем, используя структуру общего решения неоднородной системы (она была найдена при решении примера 5.5):

где — произвольные постоянные. По правилу (8.24) . Найдем пересечение подпространств и . Для этого составляем матрицу и приводим ее к ступенчатому виду

Поскольку , то размерность пересечения равна нулю: . Так как и многообразия и не пересекаются, то они скрещивающиеся.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

1

---

Подборка по базе: Рабочий лист. Формирование культурного пространства единого Росс, опыт работы по созданию и реализации проектов по созданию безопа, Общественные здания и сооружения обеспечение безбарьерности прос, Лекция 1.2.1 Цифровая грамотность педагога как основа создания е, «Особенности тушения пожаров на открытых пространствах твердых г, Создание безопасного образовательного пространства в образовател, ПР-7-Характеристика информационных систем обслуживания многозонн, «Проект по организации инклюзивного образовательного пространств, Практическая работа векторные изображения.docx, Самостоятельная работа к теме 3.6.3. Многофункциональность архит

---

Глава 4. Векторные пространства

1.Линейные векторные пространства и подпространства. Линейным вектор­ным пространством называется множество векторов, в котором определены операции умножения числа на вектор и сложения векторов вместе со своими свойствами. Размерность векторного пространства – максимальное число содержащихся в нем линейно независимых векторов.

Непустое множество линейного пространства называется линейным подпространством пространства , если для любых векторов и из выполнены условия:

где – любое действительное число.

Суммой двух подпространств и называется совокупность всех векторов пространства , которые можно представить в виде , где .

Пересечением линейных подпространств и называется совокупность векторов, которые одновременно принадлежат и . Совокупность всех векторов , ортогональных всем векторам из подпространства , называется ортогональным дополнением подпространства и обозначается .

2. Линейные многообразия. Множество всевозможных векторов вида , где вектор есть любой вектор из множества векторов называется линейным многообразием и обозначается . Линейное многообразие получено сдвигом подпространства на вектор . Вектор называется вектором сдвига, подпространство – направляющим подпространством линейного многообразия .

Свойства линейного многообразия.

1. Вектор сдвига принадлежит линейному многообразию.
2. Вектором сдвига, принадлежащим линейному многообразию, может быть любой вектор этого линейного многообразия.
3. Линейное многообразие определяется однозначно по известным подпространству и вектору сдвига .

Размерностью (рангом) линейного многообразия называется размерность линейного подпространства : .

Операции с линейными многообразиями.

1. Сумма двух линейных многообразий и есть линейное много­образие, определяемое по следующему правилу: .

1. Пересечение двух линейных многообразий и есть линейное многообразие, вычисляемое по правилу .
2. Умножение линейного многообразия на число порождает новое линейное многообразие , определяемое так: .

3. Метрические пространства. Векторное пространство называется метрическим, если задано некоторое правило, по которому каждой паре векторов ставится в соответствие некоторое число , называемое расстоянием между векторами или нормой, Оно должно удовлетворять 4 аксиомам:

1. для всех и при .

2. для всех ;

3. для

4. для всех .

Пусть и , . Модуль разности векторов может быть вычислен в координатах по-разному (разные нормы).

1. евклидова норма: .
2. октаэдрическая норма: .
3. кубическая норма: .

Формулы для вычисления расстояний в евклидовом пространстве.

Расстояние между вектором и любым вектором ,

,

где – ортогональная составляющая вектора на подпространство .

Расстояние между вектором и линейным многообразием

.

Расстояние между двумя линейными многообразиями и

.

4. Евклидовы пространства. Линейное векторное пространство называется евклидовым, если любым двум векторам и из ставится в соответствие число, обозначаемое как , причем выполняются следующие условия:

1) ; 2) ;

3) , где ; 4) , если – ненулевой вектор; , если – нулевой вектор.

Число называется скалярным произведением векторов и и определяется формулой . Длиной вектора в евклидовом пространстве называется величина . Расстоянием между векторами и является величина

Углом между ненулевыми векторами и евклидова пространства называется число , определяемое из равенства , где . Два ненулевых вектора и называются ортогональными, если .

Свойства длин векторов

1) Если вектор нулевой, то , и обратно: если , то вектор нулевой.

2) , где .

3) – неравенство Коши-Буняковского.

4) – неравенство треугольника.

Ортонормированная система векторов

Система векторов называется ортогональной, если при , и нормированной, если для всех . Если векторы системы ортогональны и нормированы, они называются ортонормированными. Если нет других указаний, векторы предполагаются разложенными по ортонормированному базису.

Теорема. Во всяком -мерном евклидовом пространстве существует ортонормированный базис.

Алгоритм последовательного построения ортонормированного базиса по заданному базису назван методом ортогонализации или процедурой Грама-Шмидта.
ПРИМЕР 1. Пусть – линейное подпространство пространства , содержащее векторы

. Вектор принадлежит . Содержится ли он в подпространстве ?

Решение. Если вектор , то он является линейной комбинацией векторов :

.

Запишем векторное равенство в развернутой матричной форме

.

Составим расширенную матрицу и приведем ее к ступенчатому виду

.

Ранги матрицы коэффициентов и расширенной матрицы не совпадают. Вектор нельзя представить в виде линейной комбинации векторов , вектор .

ПРИМЕР 2. Найти систему однородных линейных уравнений, задающую линейное подпространство, содержащее следующие векторы:

Решение.

1-й способ. Найдем ранг данной системы векторов.

.

Ранг системы равен 2, следовательно, только два вектора из четырех являются линейно независимыми, например, . Тогда линейное подпространство есть совокупность всех линейных комбинаций , где . Эту линейную комбинацию надо записать, как совокупность фундаментальных решений однородной системы уравнений, у которой переменных, из них две свободные переменные и три базисные. Следовательно, ранг системы уравнений , т. е. она должна содержать три независимых уравнения.

Для написания предварительно отдельных фундаментальных решений (линейно независимых векторов) векторы непосредственно не годятся, так как фундаментальные решения должны содержать хотя бы по одному нулю среди своих элементов. Поэтому возьмем две их линейные комбинации, например, и . Тогда общее решение некоторой однородной системы уравнений можно написать в виде:

,

а сама система уравнений будет иметь вид

или окончательно:

Конечно, задача имеет не единственное решение. Можно указать и другие системы однородных уравнений, задающие рассматриваемое подпространство.

Например, взяв линейные комбинации

и ,

получим общее решение некоторой системы линейных уравнений в виде:

.

Соответствующая система уравнений в подробном виде выглядит так:

После преобразований получим:

2-й способ. Система однородных линейных уравнений, задающая линейное подпространство, может быть найдена средствами элементарной математики. Введем произвольный вектор . Для координат вектора найдем соотношения, при которых вектор принадлежит подпространству. Разложим вектор по заданным линейно независимым векторам , как по векторам базиса подпространства, с коэффициентами .

.

В координатах векторное равенство имеет вид

,

а в виде системы уравнений

.
Выразим из системы коэффициенты α и β и подставим в остальные уравнения системы. Получим после несложных преобразований

.

Это и есть система линейных уравнений, задающая линейное подпространство.

3-й способ. Еще один способ решения задачи основан на использовании теоремы Кронекера-Капелли. Разложим вектор по заданным векторам

.

Вектор можно было бы разложить только по линейно независимым векторам, например и . Система выглядела бы проще. Однако в этом случае необходимо было бы провести предварительный анализ набора векторов по выделению из них линейно независимых векторов.

Распишем векторное равенство в координатах

Составим расширенную матрицу системы и, используя метод Гаусса, приведем матрицу к ступенчатому виду

… .

Система должна иметь решения, поскольку вектор принадлежит подпространству. Ранги матрицы коэффициентов и расширенной матрицы системы по теореме Кронекера-Капелли будут равны. Это выполняется при соблюдении условий:

Полученная система однородных линейных уравнений задает требуемое линейное подпространство.

ПРИМЕР 3. Найти линейную оболочку множества решений системы уравнений

Решение. Ранг матрицы коэффициентов системы уравнений равен 2. Выберем свободными переменными и . Тогда общее решение однородной системы уравнений имеет вид

, где .

Векторы и образуют фундаментальный набор решений однородной системы. Любое решение системы является их линейной комбинацией. Значит, линейная оболочка векторов и и есть множество решений однородной системы уравнений, т.е. , где .
ПРИМЕР 4. Найти базисы суммы и пересечения линейных подпространств, содержащих системы векторов

и .

Решение. Определим ранг каждой системы векторов:

. Ранг . . Ранг .

Для нахождения размерности суммы линейных подпространств возьмем из каждой системы векторов по два линейно независимых вектора и найдем размерность суммы этих четырех векторов

. Ранг .

Следовательно, совокупность заданных в условии векторов задает линейное подпространство размерности 3. Возьмем из первой системы векторов любые два линейно независимых вектора, например и один вектор из второй системы векторов, например . Эти векторы линейно независимы, поэтому образуют базис в 3-хмерном подпространстве.

Размерность каждой заданной системы векторов равна 2, максимальная размерность суммарной системы векторов в общем случае может быть равной 4, но оказалась равной 3, значит размерность величины 1 – это то общее, что объединяет векторы, т. е. это размерность их пересечения. Размерность пересечения двух подпространств может быть вычислена по формуле .

Найдем базис пересечения двух подпространств. Предположим что некоторый вектор принадлежит первому подпространству. Тогда справедливо разложение

.

Этот же вектор принадлежат и другому подпространству. Следовательно,

.

Приравняем правые части последних равенств

Равенство представляет линейную комбинацию из линейно независимых векторов каждой системы, зависимых в совокупности. Подберем такие значения коэффициентов, которые обращают векторное уравнение в верное равенство, для чего распишем уравнение в матричном виде и решим получающуюся однородную систему уравнений:

или .

Ее решение имеет вид: .

Пусть с=1. Найденные значения коэффициентов подставим в векторное уравнение:

.

Вектор является общим вектором для обоих подпространств. Он и может быть положен как одномерный базис подпространства, являющегося пересечением двух рассматриваемых подпространств.

ПРИМЕР 5. Найти сумму линейных многообразий и ,

где , , , , записав

в виде системы линейных уравнений.

Решение. Сумма линейных многообразий и :

.

Любой вектор , принадлежащий сумме многообразий, можно представить как

или в координатах .

Для системы уравнений с переменными и составим матрицу коэффициентов и свободных членов и проведем с ней элементарные преобразования

  

В соответствии с теоремой Кронекера-Капелли система совместна при выполнении условий

.

Полученные неоднородные линейные уравнения описывают сумму линейных многообразий в 4-хмерном пространстве. Сумма представляет собой двумерную плоскость (ранг равен 2), не проходящую через начало координат.

ПРИМЕР 6. Используя векторы , построить ортонормиро­ван­ный базис в трехмерном евклидовом пространстве.

Решение. Проверкой убеждаемся, что векторы взаимно ортогональны. Их нормировка приводит к векторам . Третий вектор должен быть ортогонален векторам . Поэтому и . Запишем эти уравнения в координатах

.

Решая систему, получим , где . Подбором коэффициента с среди бесконечного множества векторов найдем тот, длина которого равна 1. Это вектор . Легко проверить, что тройка векторов образует ортонормированный базис в трехмерном векторном пространстве.

ПРИМЕР 7. Применяя процесс ортогонализации, построить ортонормированный базис в евклидовом пространстве по заданному базису .

Решение. Нормируем вектор , в результате чего получим единичный вектор . Варьируя коэффициент , зададим новый вектор так, чтобы он был ортогонален вектору . Значение можно найти, скалярно умножив вектор на вектор и приравняв скалярное произведение нулю.

Отсюда . Следовательно, вектор имеет координаты . Он не требует нормировки, т.к. уже сам является единичным . Таким образом, ортонормированный базис имеет вид , .

ПРИМЕР 8. Линейное подпространство задано системой однородных уравнений

А) Найти базис евклидова векторного подпространства .

Б) Найти базис ортогонального дополнения .

Решение. А) Решим однородную систему уравнений, приведя матрицу коэффициентов к диагональному виду

.

Матрица коэффициентов системы уравнений с четырьмя переменными имеет ранг, равный 2. Поэтому решение будет содержать две базисные переменные и две свободные. Возьмем в качестве свободных переменные . Тогда общее решение однородной системы

будет иметь вид:

, где .

Векторы и – фундаментальные решения системы уравнений – являются линейно независимыми, поэтому задают линейное векторное подпрост­ранство размерности 2, все векторы которого есть бесконечное множество решений нашей системы.

Б) Для нахождения ортогонального дополнения к этому подпространству рассмотрим векторы , ортогональные к векторам базиса подпространства :

Соответствующая система уравнений имеет вид:

Эта система задает все векторы, ортогональные к подпространству . Ранг системы равен 2, число переменных 4, следовательно, число свободных переменных равно 2. Пусть это будут и . Тогда общее решение системы можно записать в виде:

,

где . Совокупность векторов есть линейное векторное подпространство с базисом .

Пример 8, пункт Б) может быть решен и без использования базиса векторного пространства . Путь решения состоит в следующем. Уравнения системы можно представить в виде скалярных произведений векторов на некоторые векторы

,

координаты которых составлены из коэффициентов уравнений, а именно:

Следовательно, векторы ортогональны всем векторам , то есть ортогональны подпространству и потому принадлежат подпространству . Определим среди них линейно независимые векторы:

.

Ранг матрицы равен 2. Среди векторов есть два линейно независимых вектора. Это, например и . Они и составляют базис подпространства .

Легко показать, что оба способа приводят к одному и тому же подпространству . Действительно, один из векторов двух базисов совпадает: . Другой вектор можно получить как .

ПРИМЕР 9. Найти угол между вектором и линейным подпространством , содержащим векторы .

Решение.

1-й способ. Найдем ортогональное дополнение к подпространству . Оно состоит из векторов , таких, что . Запишем эти равенства в виде системы уравнений и решим ее.

.

Решение системы имеет вид: .

Векторы и являются независимыми и составляют базис подпространства . На основе этого базиса построим ортогональный базис, т.е. проведем процесс ортогонализации полученного базиса. В качестве 1-го вектора ортогонального базиса возьмем вектор . . Тогда ортонормированный вектор . Построим вектор такой, что . Получим , или . Поэтому . Векторы и ортогональны. Легко видеть, что вектор можно было получить как . Любой вектор , ортогональный одновременно векторам и , принадлежит подпространству . Тройка векторов , и ортогональна. Пусть – углы между вектором и векторами , и соответственно. Тогда . Найдем и .

,

.

Тогда или .

Из бесконечного множества решений берем наименьший положительный угол . Это и есть угол между вектором и линейным подпространством .

2-й способ. Любой вектор пространства можно представить, причем единственным образом в виде суммы векторов из и :

, (1)

где вектор есть ортогональная проекция вектора на линейное подпространство , а вектор есть ортогональная составляющая.

Опираясь на векторы и , построим ортонормированный базис подпространства . . Используя процесс ортогонализации, получим 2-й вектор . Разложим ортогональную проекцию по ортонормированному базису подпространства : и подставим в (1).

.

Умножим обе части равенства последовательно на . Придем к соотношениям

.

Поэтому . Косинус угла между вектором и его ортогональной проекцией будет равен

.

Отсюда .

	Векторные пространства и подпространства
	Сформулировать определения линейного векторного пространства и линейного векторного подпространства.
	Сформулировать определение размерности линейного пространства. Что называется базисом линейного пространства?
	Найти размерность и базис линейных подпространств, содержащих следующие системы векторов
		3. Например
		3. Например a, c, d
		2. Например a, b
		3. Например
		3. Например
	Линейное пространство задано в виде оболочки, содержащей векторы . Принадлежит ли вектор данному пространству? Обосновать.	Да.
	Является ли множество решений уравнения линейной оболочкой векторов ?	Да
	Является ли линейным подпространством соответствующего пространства каждая их следующих совокупностей векторов:
	Все n-мерные векторы, у каждого из которых первая и последняя координаты равны между собой.	Да
	Все n-мерные векторы, у каждого из которых координаты с четными номерами равны нулю.	Да
	Все n-мерные векторы, у каждого из которых первая координата равна единице.	Нет
	Все векторы плоскости, каждый из которых лежит на одной из осей координат ОХ и ОУ?	Нет
	Все векторы плоскости, концы которых лежат на данной прямой (начало любого вектора совпадает с началом координат)?	Да, если прямая проходит через начало координат, нет в противном случае.
	Все векторы плоскости, начала и концы которых лежат на данной прямой?	Да
	Все векторы плоскости, концы которых лежат в первой четверти?	Нет
	Все векторы n-мерного векторного пространства, координаты которых – целые числа?	Нет
	Все векторы из , координаты которых удовлетворяют уравнению ?	Да
	Все векторы из , координаты которых удовлетворяют уравнению ?	Нет
	Написать в векторном виде и линейными уравнениями -мерное подпространство, проходящее через точки А, В, …., где размерность указана в условии задачи.
	, .
	, .
	.
	Найти базис подпространства, заданного уравнениями или системами уравнений
		Например,
	.	Например, .
		Например,
		Например,
		Например,
	.	Например,
	Найти размерность и какой-нибудь базис подпространства, заданного уравнением .	Размерность равна . Базис образуют, например, векторы
	Найти систему линейных уравнений, задающую линейное подпространство, содержащее следующие векторы:
		Например,
		Например,
		Например,
		Например,
	.	Векторы взяты, как фундаментальные решения некоторой системы. Тогда система имеет вид:
	.	Векторы взяты, как фундаментальные решения некоторой системы, тогда система имеет вид: .
	.	Векторы взяты, как фундаментальные решения некоторой системы, тогда система имеет вид: