Вектор состояния как найти - Сайт, где вы сможете решить свои вопросы

Вектор состояния. Амплитуда вероятности.

В рамках классической Ньютоновской механики система описывается заданием координат и импульсов всех ее составляющих. Другие свойства являются производными от основных, например, кинетическая энергия. С помощью закона Ньютона мы можем предсказать траекторию движения системы в таком фазовом пространстве. То есть изменение координат и импульсов с течением времени. Например для затухающего маятника это будет спираль.

В квантовой механике система описывается вектором соятояния, который живет в Гильбертовом пространстве. Это более абстрактный объект, чем привычный нам набор физических параметров классических систем.

В данном видео мы рассмотрим математический формализм описания векторов состояния. В последствии мы увидим как эти абстрактные векторы используются для реальных физических расчетов.

Алгебра векторов состояния идентична алгебре рассматриваемых в школьной программе векторов. Но они не имеют геометрической интерпретации в виде направленных отрезков. Несмотря на это для наглядности проведем аналогию с обычными векторами.

Вектор на плоскости можно представить направленным отрезком. Однако нам надо уйти от геометрии и характеризовать его только алгебраически. Это можно сделать задав два числа – декартовы координаты вектора. По аналогии, квантовомеханический вектор состояния, живущий в двумерном пространстве, характеризуется двумя числами – компонентами вектора. Мы запишем их в столбец.

Вектор-столбец называется кет-вектором и обозначается правой скобкой. Это просто общепринятый формализм, введенный одним из отцов-основателей квантовой механики Полом Дираком. Внутри скобок может быть что угодно. Это просто условное обозначение, поясняющее о каком векторе состояния идет речь. Аналогично обозначению обычного вектора стрелочкой над символом.

Сам вектор характеризуется набором чисел (компонентами вектора) в количестве равном размерности пространства в котором живет вектор. В нашем случае два. Эти числа в общем случае комплексные. Именно поэтому вектор состояния нельзя представить направленным отрезком. Декартовы координаты не могут быть комплексными числами.

Векторы состояния как и обычные векторы на плоскости можно складывать друг с другом и умножать на число, которое также может быть комплексным. В координатных обозначениях эти операции идентичны операциям с обычными векторами. Однако из-за замены действительных чисел комплексными, графическое представление умножения на число как увеличение длины вектора уже не работает. Как и графическое сложение по правилу параллелограмма.

В квантовой механике очень важно понятие базисных векторов. В случае обычных векторов в качестве базисных можно выбрать перпендикулярные друг другу векторы в количестве равном размерности пространства. На плоскости единичные векторы ex и ey можно выбрать в качестве базисных. Тогда любой произвольный вектор можно представить как сумму базисных, умноженных на определенные числа. В случае обычных векторов эти числа не что иное, как декартовы координаты вектора. В случае векторов состояния это компоненты вектора. В компонентных обозначениях операции сложения и умножения идентичны действиям с обычными векторами.

Следует подчеркнуть, что выбор базисных векторов отнюдь не единственен. Числовые значения компонент вектора зависят от выбранного базиса, но сам вектор (как математический объект) при смене базиса остается неизменным. В частности неизменным останется скалярное произведение векторов. Однако нам не подойдет школьная формула скалярного произведения векторов как произведения их длин на косинус угла между ними. Мы не сможем определить угол между векторами состояния, потому что они не имеют геометрического представления. Нам нужно все перевести на язык алгебры.

Векторы (как и матрицы) перемножаются по правилу «строка на столбец». Мы можем перевести столбец в строку посредством рассматриваемой в прошлом видео операции эрмитового сопряжения, обозначаемой крестиком. Тогда скалярное произведение запишется как произведение вектор-строки на вектор-столбец. Заметьте, что мы получили аналог школьной формулы для скалярного произведения как суммы произведений соответствующих декартовых координат векторов. Но поскольку компоненты векторов состояния являются комплексными числами, из-за эрмитового сопряжения у нас добавилась операция комплексного сопряжения, обозначаемая звездочкой. В случае обычных чисел комплексное сопряжение ничего не делает и мы получим привычную школьную формулу для скалярного произведения.

Эрмитово-сопряженный кет-вектор обозначается левой скобкой и называется бра-вектор. Поскольку эрмитово сопряжение помимо замен столбцов на строки включает еще и комплексное сопряжение, то в разложении вектора по базисным, мы видим комплексно-сопряженные компоненты. Скалярное произведение обозначается совмещением бра- и кет- векторов и называется в квантовой механике амплитуда вероятности по причинам, которые будут ясны в дальнейшем.

Названия предложены Дираком и являются разложением слова брэкет на две части бра- и кет-.

Скалярное произведение интересно во многих отношениях. Скалярное произведение двух векторов дает не вектор, а число (в общем случае комплексное). То есть амплитуда вероятности это комплексное число. Произведение вектора a на b равно комплексному сопряжению произведения b на a.

Заметьте, что даже если компоненты вектора состояния являются комплексными числами, то скалярное произведение вектора с самим собой — это действительное неотрицательное число. Действительно, входящие в формулу произведения комплексных чисел на свои сопряжения это действительные числа — квадраты модулей комплексного числа. Для обычных векторов скалярное произведение вектора с самим собой это квадрат длины вектора.

Еще одно интересное свойство скалярного произведения: Если скалярное произведение двух векторов равно нулю, то для обычных векторов это означает, что они перпендикулярны. В случае векторов состояния говорят, что они ортогональны. Можно, например, убедиться, что базисные векторы ex и ey ортогональны.

И наконец, компонента вектора равна скалярному произведению данного вектора с соответствующим этой компоненте базисным вектором. Для обычных векторов это свойство наглядно поскольку скалярное произведение векторов можно представить как проекцию одного вектора на направление другого. То есть коэффициенты в разложении вектора состояния по базисным векторам являются амплитудами вероятности.

ВЕ́КТОР СОСТОЯ́НИЯ

В книжной версии

Том 4. Москва, 2006, стр. 710

Скопировать библиографическую ссылку:

ВЕ́КТОР СОСТОЯ́НИЯ, физическая величина, характеризующая возможное состояние квантовой системы; одно из осн. понятий квантовой механики . В отличие от классич. механики, где движение тел описывается экспериментально измеримыми величинами – наблюдаемыми (координатами, импульсом, моментом импульса, энергией и т. д.), в квантовой механике результаты измерений той или иной величины предсказываются лишь вероятностно. Все возможные состояния данной системы образуют пространство состояний (бесконечномерное гильбертово пространство ), элементами которого и являются В. с. Как и в математике, В. с. можно складывать, получая новые возможные состояния ( суперпозиции принцип ), умножать на комплексные числа, каждой паре В. с. сопоставляется комплексное число – их скалярное произведение.

6.5. Вектора: целей, состояния, ошибки управления, их соотношение

Для осознанной постановки и решения каждой из названных ранее или обеих задач теории управления совместно (когда одна сопутствует другой или они некоторым образом взаимно проникают друг в друга) необходимы три набора информации: вектор целей, вектор состояния, вектор ошибки управления.

Вектор[1] целей управления (а равно — самоуправления, где не оговорено отличие), представляющий собой описание идеального режима функционирования (поведения) объекта (процесса).

Вектор целей управления строится по субъективному произволу как иерархически упорядоченное множество частных целей управления, которые должны быть осуществлены в случае идеального (безошибочного) управления. Порядок следования частных целей в нём — обратный порядку последовательного вынужденного отказа от каждой из них в случае невозможности осуществления полной совокупности целей. Соответственно на первом приоритете вектора целей стоит самая важная цель, на последнем — самая незначительная, отказ от которой допустим первым.

Образно говоря, вектор целей — это список, перечень того, чего желаем, с номерами, назначенными в порядке, обратном порядку вынужденного отказа от осуществления каждого из этих желаний. Если несколько целей представляются равнозначными, то они в совокупности образуют интегральную цель на соответствующем приоритете вектора целей.

Одна и та же совокупность целей, подчинённых разным иерархиям приоритетов (разным порядкам значимости для управленца), образует разные вектора целей, что ведёт и к возможному различию в управлении, в том числе и вследствие возникновения различий в построении критериев оптимальности управления и расчёте их значений.

Дефективность вектора целей может быть возможной причиной низкого качества управления (вплоть до полной потери управления). Основные типы дефектов вектора целей приведены ниже:

выпадение из вектора некоторых целей, объективно необходимых для управления процессом;
выпадением всего вектора или каких-то его фрагментов из объективной матрицы возможных состояний объекта;
наличие в нём целей, объективно и субъективно взаимно исключающих друг друга;
наличие целей, неустойчивых в процессе управления (способных исчезать в процессе управления или утрачивать актуальность);
ошибки в иерархической упорядоченности целей в составе вектора:
ошибочное задание приоритетов целей, в результате чего цели, приоритеты которых для успешного решения задачи управления должны быть ниже, обладают более высокими приоритетами, чем действительно значимые цели (один из вариантов — привязка низкоприоритетных по их существу целей к высокоприоритетным, в результате чего приоритеты каких-то целей могут быть занижены, а каких-то завышены, и на каком-то из приоритетов вектора целей образуется дефективная интегральная цель);
наличие нескольких экземпляров одних и тех же целей на разных приоритетах;
«закольцованность» иерархии значимости целей (либо её фрагментов)[2].

Вектор целей управления может изменяться в процессе управления, будучи функцией времени (в обыденном понимании этого явления) либо функцией матрицы возможностей течения процесса управления (объективной меры бытия, как составляющей триединства материи-информации-меры) и субъективно избранной алгоритмики управления процессом. В этом случае вектор целей, строго говоря, не является «вектором» в математическом понимании этого термина, поскольку представляет собой множество векторов, характеризующих разные этапы процесса управления, упорядоченное в соответствии: 1) с матрицей возможностей и 2) разветвлениями алгоритмики управления процессом. Эта тема поясняется далее в комментариях к рис. 6.13-4 (в разделе 6.13). Памятуя об этом несоответствии терминологии ДОТУ нормам математики, мы, тем не менее, распространим и на этот случай употребление термина «вектор целей управления».

В некоторых версиях теории управления по отношению к этому случаю употребляется термин «дерево целей», что подразумевает наличие преемственной последовательности целей, которая может разветвляться в процессе управления, и которые должны быть осуществлены в ходе реального управления на разных этапах процесса. Однако и вариант с «деревом целей» не отвечает требованию универсальности терминологии, поскольку, как показывает практика применения аппарата сетевого планирования, процесс управления может не только разветвляться, но и разного рода частные процессы управления могут сливаться воедино по достижении каких-то общих промежуточных для них целей. В этом случае можно было бы именовать совокупность целей термином «сеть целей», однако он интуитивно непонятен. Поэтому мы отдаём предпочтение расширительному толкованию термина «вектор целей управления», включая в него и тот случай, когда вектор целей может изменяться в процессе управления, будучи функцией времени либо функцией матрицы возможностей течения процесса управления и субъективно избранной алгоритмики управления процессом.

Вектор (текущего) состояния имеет более сложную структуру, нежели вектор целей. Первый его блок — блок контрольных параметров, который вбирает в себя информацию, характеризующую реальное поведение объекта по параметрам, входящим в вектор целей.

Каждый из контрольных параметров в этом блоке может быть представлен в виде суммы трёх составляющих: первая характеризует «полезную отдачу» замкнутой системы (процесса управления), вторая представляет собой «собственные шумы» замкнутой системы, а третья — помехи, наводимые в ней извне. Собственные шумы системы и помехи, наводимые в ней извне, так или иначе снижают качество управления и потому их можно выделить в отдельные компоненты вектора текущего состояния, что породит соответствующие им компоненты в составе вектора целей. такой подход потребует и соответствующих управленческих мер, направленных на снижение уровней собственных шумов и помех в контрольных параметрах.

Либо при другом подходе к структурированию информации собственные шумы и помехи могут быть перенесены в правую часть уравнения на схеме рис. 6.5-1 — в состав вектора ошибки управления.

Названные два вектора (целей и состояния) образуют взаимосвязанную пару, в которой каждый из этих двух векторов представляет собой упорядоченное множество информационных модулей, описывающих те или иные параметры объекта, определённо соответствующие частным целям управления. Упорядоченность информационных модулей в векторе состояния повторяет иерархию вектора целей. Образно говоря, вектор состояния это — список, как и первый, но того, что воспринимается в качестве состояния объекта управления, реально имеющего место в действительности.

В подавляющем большинстве случаев непосредственное воздействие на параметры, входящие в вектор целей управления, оказывается невозможным. Именно это обстоятельство и вызывает потребность в организации управления путём решения задачи об устойчивости в смысле предсказуемости поведения и выявления параметров, на которые возможно оказать непосредственное воздействие, следствием которого будет желательное изменение контрольных параметров, входящих в вектор целей.

Реализация такого подхода (в подавляющем большинстве случаев неизбежного) приводит к тому, что размерность вектора состояния больше, чем размерность вектора целей за счёт включения в него параметров, связанных в матрице возможных состояний с параметрами, включёнными в вектор целей. Эти дополнительные параметры можно разделить на две группы:

В первую входят параметры, которые поддаются непосредственному изменению. Из их перечня выбираются параметры, на которые в процессе управления будет оказываться управляющее воздействие. Это — непосредственно управляемые параметры, изменение которых влечёт за собой изменение параметров, включённых в вектор целей. Эти параметры образуют вектор управляющего воздействия. В ряде случаев непосредственно управляемые параметры могут входить в состав вектора целей (например, на кораблях при больших скоростях хода, чтобы предотвратить недопустимый крен в процессе поворота, а то и опрокидывание корабля, могут налагаться ограничения на угол перекладки руля, который в задачах управления маневрированием, в отличие от угла курса, скорости хода, координат, обычно не входит в перечень контрольных параметров).
Во вторую группу входят так называемые «свободные параметры», любые возможные значения которых в процессе управления признаются допустимыми (если бы на них накладывались какие-либо ограничения, то они с этими ограничениями вошли бы в вектор целей).

Поскольку восприятие субъектом состояния объекта не идеально (во-первых, в силу искажения информации, исходящей от объекта, «шумами» среды, через которую проходят информационные потоки; во-вторых, оно носит характер, обусловленный особенностями субъекта в восприятии и переработке информации), вектор состояния всегда содержит в себе некоторую ошибку в определении истинного состояния, которой соответствует некоторая объективная неопределённость для субъекта управленца. Неопределённость объективна, т.е. в принципе не может быть устранена усилиями субъекта. Другое дело, что объективная неопределённость может быть как допустимой, так и недопустимой для осуществления целей конкретного процесса управления.

Вектор ошибки управления представляет собой «разность» (в кавычках потому, что разность не обязательно привычная алгебраическая): «вектор целей» – «вектор состояния». В него могут входить как измеримые отклонения вектора состояния от вектора целей, так и оценки (как это показано на схеме рис. 6.5-1 — ниже по тексту), необходимость в которых может возникать вследствие того, что вектор текущего состояния включает в себя некоторую неопределённость. Вектор ошибки управления описывает отклонение реального процесса от предписанного вектором целей идеального режима и также несёт в себе некоторую неопределённость, унаследованную им от вектора состояния. Образно говоря, вектор ошибки управления это — перечень неудовлетворённых желаний соответственно перечню вектора целей с какими-то измерениями или оценками степени неудовлетворённости каждого из них. Оценки могут быть построены на основе соизмеримых друг с другом численно уровней, либо численно несоизмеримых уровней, но упорядоченных ступенчато дискретными целочисленными индексами предпочтительности каждого из уровней в сопоставлении его со всеми прочими уровнями.

Помимо исходного различия вектора целей и вектора состояния в момент начала управления источниками ошибок управления реально являются: 1) алгоритмика выработки управляющего воздействия системой управления, которая в принципе не может гарантировать идеального управления с нулевыми компонентами вектора ошибки, 2) собственные шумы в замкнутой системе[3], 3) помехи извне, включающие в себя воздействие среды, а также и целенаправленные попытки перехвата управления со стороны иных субъектов.

Структура и соотношение информации, входящей в перечисленные вектора, характеризующие процесс управления, показаны на схеме рис. 6.5-1, приведённой ниже.

Если эту форму не удаётся заполнить метрологически состоятельной информацией, то это — показатель того, что задача управления не может быть даже поставлена, а не то, что решена.

Рис. 6.5-1. Структурирование информации, характеризующей процесс управления

Задача управления в своём существе — достичь целей, а равно — обнулить вектор ошибки управления.

Реально вектор ошибки не может быть сделан идеально нулевым как вследствие объективных причин, так и вследствие разного рода неточностей и запаздываний в процессе управления, которые обусловлены субъективными причинами в ходе организации управления. Соответственно этому обстоятельству реальное управление может протекать в одном из трёх режимов:

Нормальное управление — в нём реально ненулевые значения компонент вектора ошибки управления оцениваются как вполне приемлемые (они могут при этом находиться в пределах погрешности измерений — в этом случае достигаются значения так называемого «технического нуля» либо могут считаться приближённо равными нулю[4]).
Допустимое управление — в нём реально ненулевые значения компонент вектора ошибки находятся в пределах, признаваемых допустимыми, но допустимое управление по своим характеристикам хуже, чем нормальное.
Аварийное управление — в нём те или иные компоненты вектора ошибки выходят за допустимые пределы, но катастрофа управления (необратимая потеря управления, повреждения, разрушение объекта управления или нанесение им ущерба элементам внешней среды) ещё не наступила. В режиме аварийного управления главной целью управления становится возвращение объекта хотя бы в режим допустимого управления.

Аварийное управление — один из тех случаев, в которых иерархическая упорядоченность компонент вектора целей и его состав могут изменяться в процессе управления, что влечёт за собой изменение и всей структуры информации в задаче управления.

Разграничение нормального и допустимого управления носит либо субъективно обусловленный характер, либо диктуется самой задачей управления.

Также надо понимать, что в силу субъективизма управленцев, формула взаимосвязи трёх названных векторов, приведённая на схеме рис. 6.5-1 («вектор целей» – «вектор состояния» = «вектор ошибки управления»), допускает обмен местами в ней «вектора целей» и «вектора ошибки управления»: т.е. возможны ситуации, в которых вектор состояния, который с точки зрения одного субъекта-управленца — ошибка управления, для другого — успешно достигнутая цель.

[1] В наиболее общем случае под термином «вектор» подразумевается — не отрезок со стрелочкой, указывающей направление, а упорядоченный перечень (т.е. с номерами) разнокачественной информации. В пределах же каждого качества должна быть определена хоть в каком-нибудь смысле мера качества. Благодаря этому сложение и вычитание векторов обладают некоторым смыслом, определяемым при построении векторного пространства параметров. Именно поэтому вектор целей — не дорожный указатель «туда», хотя смысл такого дорожного указателя и близок к понятию «вектор целей управления». Кроме того компонентами вектора целей могут быть не константы, а функции одного или более аргументов.

[2] «Закольцованность» рангов имеет место в некоторых карточных играх: самая слабая карта — шестёрка, но только она бьёт туза. Аналогично этому может иметь место «закольцованность» иерархической упорядоченности по значимости целей в их полном перечне. Если «закольцованность» — неизбежность, то возможно разделение управленческой задачи на последовательные этапы, на каждом из которых «закольцованность» разрывается и иерархия вектора целей обретает определённость.

[3] Замкнутая система — объект управления и система управления им, связанные друг с другом каналами обмена информацией.

[4] Однако при этом надо помнить, что с точки зрения вычислительной математики два ЛЮБЫХ числа приближённо равны, и потому практически вопрос только в том: можно ли в осуществляемом процессе управления ненулевые компоненты вектора ошибки считать приближённо нулевыми?

[spoiler title=”источники:”]

http://bigenc.ru/physics/text/1904091

6.5. Вектора: целей, состояния, ошибки управления, их соотношение

[/spoiler]

Источник

Седьмая часть серии видео элементарного введения в квантовую механику.

Названия предложены Дираком и являются разложением слова брэкет на две части бра- и кет-.

Источник

Существует множество специальных
приемов, позволяющих упрощать проведение
вычислений с амплитудами вероятности.
Совокупность этих приемов составляет
математический
аппарат квантовой механики. Этот
аппарат основан на использовании ряда
математических понятий, правильное
применение которых требует предварительного
анализа их содержания и смысла.

Вектор состояния

Центральное место в математическом
аппарате КМ занимает понятие “вектор
состояния”. Для его анализа используем
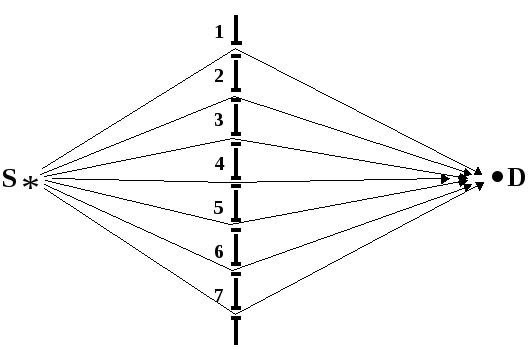
мысленный эксперимент. Приготовим
устройство, включающий источник и
детектор, между которыми расположен
экран (произвольной формы) с множеством
микроскопических отверстий.

Интересующее нас событие S→Dможет осуществиться
несколькими альтернативными способами.
Каждый из них представляет собой
последовательность двух элементарных
событий. Правило расчета глобальной
амплитуды в такой ситуации известно:

А_S_→_D
= 
D | S
 = 
D | 1
 
 1
| S 
+  D
| 2 
 2
| S 
+ . . . . =

= D|ii |S=
(D_iS_i)

Из этой формулы видно, что амплитуда
А_S_→_Dполучается в результате комбинирования
двух групп комплексных чисел:

числа типа S_i
=i|S,
каждое из которых характеризует одно
из отверстий экрана по отношению к
источнику, а именно представляет собой
амплитуду попадания частицы из источникаSв данное отверстие
с номеромi ;
числа типа D_i=D|i,
каждое из которых характеризует одно
из отверстий экрана по отношению к
детектору, а именно: представляет собой
амплитуду попадания частицы из отверстия
с номеромi в
детектор D.

Наборы чисел {S_i}
и {D_i}
можно рассматривать лишь как необходимые
компоненты для вычисления глобальной
амплитуды, но можно приписать им
определенный смысл и самим по себе,
поскольку эти два набора в определенном
отношении независимы друг от друга.

Если в рассмотренной выше экспериментальной
установке переместить источник в другую
точку пространства то изменятся все
расстояния от источника до отверстий
экрана, а, следовательно, изменятся и
все амплитуды типа S_i=i|S.
При этом, однако, все амплитуды второго
типаD_i=D|i,
останутся теми же самыми, поскольку
положение детектора относительно экрана
не изменилось. Аналогичную процедуру
можно проделать и с детектором, оставив
источник в прежнем положении. При этом
все числа типа D_i=D|iизменятся, но числаS_i=i|S,
связанные с источником, останутся
неизменными.

Отсюда следует важный вывод:

числа S_i=i|S
характеризуют состояние частиц,
приготавливаемых источником —
начальное
состояние| S
,
числа D_i=D|iхарактеризуют состояние частиц в месте
расположения детектора —
конечное
состояние D| .

Подчеркнем, что начальное и конечное
состояния частиц характеризуются не в
универсальном смысле, а лишь некоторым
конкретным способом — с точки зрения
прибора, расположенного между источником
и детектором (в данном случае — экран
с отверстиями). Достаточно очевидно,
что при использовании другого прибора
мы получим аналогичное описание обеих
состояний (начального и конечного), но
наборы чисел {S_i}
и {D_i},
будут другими.

Такое описание состояния микрообъектов
посредством набора чисел-амплитуд и
называется “вектором состояния”.
Происхождение такого названия обусловлено
аналогией между рассмотренными выше
наборами чисел-амплитуд и обычными
математическими векторами. Рассмотрим
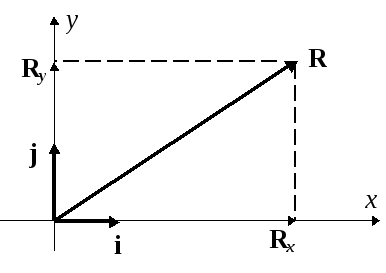
для примера вектор на плоскости. Для
его описания удобно использовать систему
координатных осей, например, декартовых:

Каждая декартова ось порождается
некоторым специальным
базисным вектором,имеющим заданное направление и единичную
длину. Для анализа произвольного вектораRнужно сначала
спроектировать его на координатные оси
и найти две проекции:R_x
и R_y,
сумма которых и дает векторR:

R=R_x+R_y

Второй этап анализа заключается в том,
что проекции вектора сравнивают по
длине с соответствующими базисными
векторами, длина которых принимается
за единицу. Это приводит к представлению
вектора в виде линейной комбинации
базисных векторов:

R=R_x+R_y= x
i + y j

Пользуясь одним и тем же набором базисных
векторов (системой координат), мы можем
проанализировать подобным образом
любой вектор. При этом все описания
будут выглядеть однотипно, отличаясь
только набором чисел (x,y), которые называются
координатамивектора в выбранном базисе (i,
j). Поэтому в рамках
заданной координатной системы не только
каждый вектор можно охарактеризовать
набором чисел-координат:R= (x, y),
и наоборот, каждый такой набор чисел
можно рассматривать как вектор (x,
y) =R.
Отсюда и вытекает интерпретация наборов
чисел-амплитуд как векторов:

вектор начального состояния | S
 = (S₁,S₂, … )
вектор конечного состояния 
D | = (D₁,D₂, … )

Рассмотренная аналогия между
математическими векторами и векторами
состояния простирается очень далеко.
Так, для математических векторов
определена специальная операция —
“скалярное умножение”. Она выполняется
следующим образом. Один из
векторов-сомножителей записывают в
виде вектора-строки, а второй — в виде
вектора-столбца, затем попарно перемножают
координаты с одинаковыми номерами, а
полученные произведения складывают:

Результатом скалярного умножения двух
векторов является единственное число
Z(скаляр), называемое
скалярным
произведениемвекторовАиВ.
Легко заметить полное сходство между
конструкцией скалярного произведения
и схемой вычисления амплитуды через
векторы начального и конечного состояний:

А_S_→_D=D|S=D|1 1|S+D|22|S+ . . . . =

= D|ii |S=
(D_iS_i)

Отсюда можно заключить:

глобальная амплитуда некоторого
события (квантового перехода) всегда
может быть представлена в виде скалярного
произведения двух векторов, изображающих
начальное и конечное состояния.

Символ, введенный выше для обозначения
амплитуды D|Sможно рассматривать как “произведение”
двух символов, изображающих отдельные
векторы-сомножители: D | S
 =D||S.
При этом очевидно, что первый сомножитель
эквивалентен вектору-строке, а второй
— вектору-столбцу. Существует общепринятое
соглашение:

векторы начальных состояний всегда
следует рассматривать как векторы-столбцы
и обозначать их правой угловой скобкой
| S(“кет-вектор”);
векторы конечных состояний всегда
следует рассматривать как векторы-строки
и обозначать их левой угловой скобкой
D| (“бра-вектор”);
cкалярное произведение
двух векторов состояния всегда должно
выглядеть как полная угловая скобкаD|S(“бра-кет” — от английскогоbracket— скобка).

Таким образом, можно сделать несколько
промежуточных выводов:

1) Любое квантово-механическое состояние
можно изобразить с помощью математического
объекта — вектора состояния.

2) Любой КМ-вектор состояния можно
проанализировать особым способом —
представить в виде линейной комбинации
некоторых базисных векторов, и описать
набором чисел-координат.

3) Любое КМ-событие можно представить в
виде перехода из одного состояния в
другое, причем амплитуда этого события
может быть вычислена как скалярное
произведение соответствующих векторов
состояния.

Соседние файлы в папке лекции (текст)

Источник

Предыдущие посты

Теперь нам не помешает перекинуть мостик между этими рассуждениями и теми, что обычно встречаются в учебных и научно-популярных наставлениях по квантовой механике. Там фигурирует такое понятие как «вектор квантового состояния». Речь, на самом деле, о том, что для описания поведения квантовых состояний используется математика, почти полностью аналогичная векторной алгебре. То есть, вектор квантового состояния – это не более чем удобная математическая модель.

Мы тут говорили, что воздействие «расщепляет» группы виртуальных вариантов, а в традиционном изложении квантовых премудростей толкуют о том, что воздействие поворачивает вектор квантового состояния. Как мы сейчас убедимся, между этими двумя подходами нет никакого противоречия. Если рассуждать на абстрактном математическом языке, то вектор – это набор определённым образом упорядоченных чисел. Например, если мы говорим о векторе на обычной (декартовой) плоскости, то это всего два числа. Взгляните на рисунок 17.7.

Да, когда про вектора рассказывают в школе, там применяют для них другие обозначения, типа буквы с чёрточкой над ней. Но мы, дабы не множить сущностей, будем обозначать вектора так, как принято в квантовой механике. Так вот, вектор |A〉 легко проецируется на оси координат, и эти проекции тоже являются векторами |A_x〉 и|A_y〉. Разумеется, вектор является суммой собственных проекций, поэтому справедливо следующее:

|A〉 = |A_x〉 + |A_y〉 (ф. 17.10).

Дальше, никто нам не мешает ввести ещё два вектора определённой длины, параллельных координатным осям. На рисунке 17.8 они показаны зелёным цветов и обозначены как |x〉 и |y〉, прошу не путать с обозначениями координатных осей.

Эти вектора, |x〉 и |y〉, мы примем за базисные. Что касается длины базисных векторов, её можно выбрать произвольно, но удобнее брать единичную длину. Тогда можно записать:

|A_x〉 = a_x|x〉
|A_y〉 = a_y|y〉

Где a_x – это действительное число, выражающее соотношение длин вектора |A_x〉 и базисного вектора |x〉, a_y – это, соответственно, соотношение длин |A_y〉 и |y〉. Подставляя это в (ф. 17.10), получаем:

|A〉 = a_x|x〉 + a_y|y〉 (ф. 17.11).

a_x, a_y – это и есть те самые два заветных числа, которые определяют вектор |A〉. Можно сказать так: эти числа определяют, в какой пропорции вектор |A〉 содержит базисные вектора |x〉 и |y〉. Заметим, что в этом базисе можно выразить абсолютно любой вектор, лежащий на декартовой плоскости, при этом коэффициенты a_x, a_y (эти числа называют ещё – координаты вектора) будут, разумеется, для каждого вектора свои.

Теперь соотнесите всё это с тем, о чём мы рассуждали выше. Например, если мы сравним выражения (ф. 17.11) и (ф. 17.1), то увидим почти полную аналогию. Почти – потому что вектора квантовых состояний выражаются в комплексных числах и «существуют» не в декартовом, а в особенном пространстве, именуемом пространством Гильберта. Тем не менее, вектора квантовых состояний подчиняются практически тем же математическим правилам, что и обычные вектора. Их можно умножать на число, складывать, поворачивать в пространстве. Опять же, по аналогии с традиционными векторами, вектор любого квантового состояния…

Отставить, не любого. Вектором можно представить только так называемые чистые квантовые состояния. Бывают ещё смешанные состояния, которые вектором не опишешь. О их мы поговорим ещё, а пока рассматриваем только чистые состояния.

Так вот, вектор любого ЧИСТОГО квантового состояния может быть представлен в виде суммы векторов базисных состояний, взятых в определённых пропорциях. В принципе, за базисные можно принять любые два различных квантовых состояния, но в большинстве ситуаций за базисные выбираются те состояния, которые дают однозначный результат измерения. В случаях, которые мы тут разбирали, это состояния |0⁺〉 и |0^–〉.

Надо отметить одну особенность векторов квантовых состояний, которая сильно облегчает жизнь при квантовых расчётах: модуль (длина) вектора
квантового состояния всегда равняется единице.

Теперь о «расщеплении» состояний при воздействии. Продолжая аналогию с векторами, можно сказать, что изменение состояния при воздействии аналогично повороту вектора в пространстве. Продемонстрируем это.

На рисунке 17.9 показано, как влияет на базисные вектора (сейчас мы говорим про обычные вектора на декартовой плоскости) поворот не угол 𝛗 по часовой стрелке.

Глядя на картинки, запишем:

[𝛗]|x〉 = 𝛗^xx|x〉 + 𝛗^xy|y〉
[𝛗]|y〉 = 𝛗^yx|x〉 + 𝛗^yy|y〉

Пожалуйста, наблюдаем «расщепление» аналогичное тому, которое мы наблюдали при воздействии магнитного поля на базисные квантовые состояния |0⁺〉 и |0^–〉, сравните с (ф. 17.2).

Четыре коэффициента «расщепления» образуют матрицу поворота:

В данном случае коэффициенты расщепления, кстати, легко вычислить из элементарной тригонометрии, и вот что получится:

Но сейчас не об этом. Сейчас о том, что зная матрицу поворота, то есть, зная то, как поворот [𝛗] действует на базисные вектора, мы легко сможем вычислить действие этого поворота на произвольный вектор. Смотрите, допустим у нас есть вектор:

|A〉 = a_x|x〉 + a_y|y〉

Что произойдёт, если мы повернём этот вектор на угол 𝛗 по часовой стрелке? Чтобы узнать это, действуем так же, как мы действовали при вычислении квантового состояния |S_W₁_W₁〉, вернитесь к (ф. 17.6):

[𝛗]|A〉 = [𝛗](a_x|x〉) + [𝛗](a_y|y〉) = a_x₍[𝛗]|x〉) + a_y₍[𝛗]|y〉) =
= a_{x (}𝛗^xx|x〉 + 𝛗^xy|y〉) + a_y(𝛗^yx|x〉 + 𝛗^yy|y〉) =
= a_x𝛗^xx|x〉 + a_x 𝛗^xy|y〉 + a_y𝛗^yx|x〉 + a_y𝛗^yy|y〉 =
= (a_x𝛗^xx + a_y𝛗^yx)|x〉 + (a_x𝛗^xy + a_y𝛗^yy)|y〉

Вот вам векторная алгебра «на пальцах». Как уже сказано, квантовые состояния при воздействиях ведут себя так же и подчиняются той же математике. Правда, с обычными векторами вся эта «поворотная» математика достаточно наглядна (надеюсь мне удалось это показать). С векторами квантового состояния такой наглядности нет, поскольку невозможно представить себе даже двухмерное комплексное пространство, не говоря уже о многомерных. Представить нельзя, но вычислить можно, чем мы и занимались в этой части.

В общем, я предлагаю так: физически представляем себе всё эту «кухню» с воздействиями всё-таки как расщепление – воссоединение групп виртуальных вариантов. А векторную математику используем как подспорье для точного вычисления того, как именно они расщепляются – воссоединяются.

Проведём небольшую систематизацию всех типов векторов, которые мы вводили по ходу ликбеза.

1. Квантовый вектор отдельного виртуального варианта. Это вектор в условном пространстве типа «комплексная плоскость» или, если угодно, просто комплексное число. По сути дела, координатами квантового вектора на комплексной плоскости являются реальная и мнимая части комплексного числа. Мы определились, что модули (длины) квантовых векторов всех виртуальных вариантов равны между собой и равны некой условной единице.

2. Амплитуда вероятности группы – векторная сумма квантовых векторов всех виртуальных вариантов группы. Тип пространства этого вектора тот же самый, что и у квантовых векторов виртуальных вариантов группы – комплексная плоскость. Кстати говоря, разные группы вариантов существуют в разных пространствах, как единица и шестёрка игральной кости существуют на разных плоскостях кубика. Именно поэтому квантовые вектора виртуальных вариантов, относящихся к разным группам, не вступают в состояние суперпозиции.

3. Вектор квантового состояния, мы его изучали в этой части. Это уже другой тип пространства, а именно – пространство Гильберта. В обычном декартовом пространстве, как вы знаете, координаты точки, а значит и координаты векторов, задаются действительными числами. А в гильбертовом пространстве координаты – это комплексные числа. В частности, координатами вектора состояния являются амплитуды вероятности базисных квантовых состояний. Поскольку вектор квантового состояния является суперпозицией векторов базисных состояний, то вектора предыдущего уровня – амплитуды вероятности – участвуют в этой суперпозиции исключительно как коэффициенты, определяющие, в какой пропорции (комплексной, в общем случае) то или иное базисное состояние входит в рассматриваемое квантовое состояние.

Всё, больше никаких типов векторов мы вводить не будем, этого достаточно.

В следующей части мы немного отдохнём от математики и разберём несколько знаменитых квантовых опытов с высоты обретённых знаний. А по этой части мне хотелось бы знать, понятно ли я изложил материал? Если неясностей тут для вас нет – дальше всё пойдёт, как по маслу.

Продолжение

Источник

Вектор состояния. Амплитуда вероятности.

ВЕ́КТОР СОСТОЯ́НИЯ

6.5. Вектора: целей, состояния, ошибки управления, их соотношение

Вектор состояния

Вам также может понравиться

Как найти полосу пропускания полосового фильтра

Как найти водителя по перевозке груза

Как найти юриста не мошенника

Добавить комментарий Отменить ответ