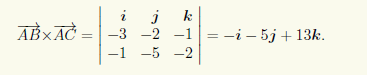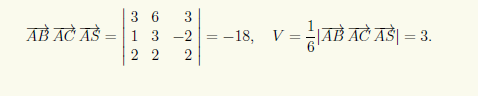Объём параллелепипеда
равен
смешанному произведению векторов
на которых он построен:
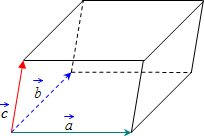
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела – всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Объём параллелепипеда
Объём параллелепипеда, построенного на трех векторах
где координаты векторов в соответствии с рисунком
вычисляются следующим образом
Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.
Найти объём параллелепипеда, построенного на векторах a1=<2;3;2>, a2= <-1;-4;3>и a3=
$ = pm left( <2cdotleft( <left( < — 4>right)cdot2 — 1cdot3> right) — 3left( <left( < — 1>right)cdot2 — 3cdot3> right) + 2left( <left( < — 1>right)cdot1 — 3cdotleft( < — 4>right)> right)> right) = -33$
Так как определитель отрицателен, берем перед ним знак « − ».
Тогда объём параллелепипеда построенного на векторах равен V=33
Объем параллелепипеда, построенного на векторах онлайн
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела – всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
|
= | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
|
= | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
|
= | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
|
= |
|
= |
|
= |
|
. |
|---|
| cos(λ1) | = |
|
. |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
|
= |
|
. |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
|
= |
|
. |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
[spoiler title=”источники:”]
http://mathforyou.net/online/vectors/volume/parallelepiped/
http://matemonline.com/primeru/zada4a-na-vektor/
[/spoiler]
Skip to content
Объём параллелепипеда, построенного на трех векторах
a1={X1;Y1;Z1}, a2={X2;Y2;Z2} и a3={X3;Y3;Z3} равен модулю смешанного произведения векторов и находится по формуле:
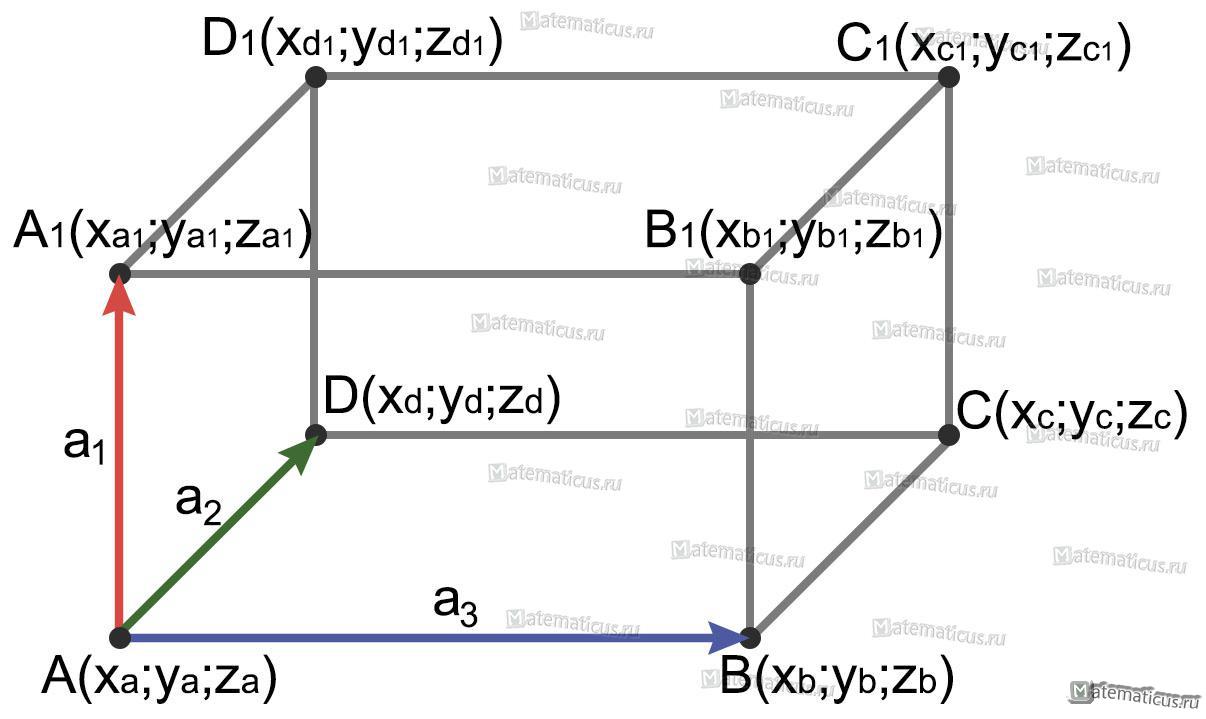
где координаты векторов в соответствии с рисунком
вычисляются следующим образом
a1=$overrightarrow {AA_1} $={X1=Xa1-Xa; Y1=Ya1-Ya; Z1=Za1-Za; }
a2=$overrightarrow {AD} $={X2=Xd-Xa; Y2=Yd-Ya; Z2=Zd-Za; }
a3=$overrightarrow {AB} $={X3=Xb-Xa; Y3=Yb-Ya; Z3=Zb-Za; }
Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.
Пример
Найти объём параллелепипеда, построенного на векторах a1={2;3;2}, a2={-1;-4;3} и a3={3;1;2}
Решение
$V = pm left| {begin{array}{*{20}{c}}2&3&2 \ { — 1}&{ — 4}&3 \ 3&1&2 end{array}} right| = pm left( {2left| {begin{array}{*{20}{c}} { — 4}&3 \ 1&2 end{array}} right| — 3left| {begin{array}{*{20}{c}}{ — 1}&3 \ 3&2 end{array}} right| + 2left| {begin{array}{*{20}{c}}{ — 1}&{ — 4} \ 3&1 end{array}} right|} right) = $
$ = pm left( {2cdotleft( {left( { — 4} right)cdot2 — 1cdot3} right) — 3left( {left( { — 1} right)cdot2 — 3cdot3} right) + 2left( {left( { — 1} right)cdot1 — 3cdotleft( { — 4} right)} right)} right) = -33$
Так как определитель отрицателен, берем перед ним знак «−».
Тогда объём параллелепипеда построенного на векторах равен V=33
16860
Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.
Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.
Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).
Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.
Затем по (3.2) вычислим их векторное произведение:
Модуль этого векторного произведения равен |AB×AC| = √((—1)2 + (—5)2 + 132) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #
Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.
Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).
Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов:
Решение
По
формуле (2.33)
.
,
так как соединяет точку
с началом координат. По условию
.
По
формуле
Т.о.,
.
Смешанное произведение трех векторов
Определение
Смешанным произведением трех векторов
и
называется число, полученное, если
перемножить векторыи
векторно,
а потом полученный вектор умножить
скалярно на вектор.
Поэтому это произведение еще называется
векторно-скалярным произведением.
Смешанное произведение записывается
таким образом:,
т.е..
С
геометрической точки зрения смешанное
произведение некомпланарных векторов
и
по модулю равно объему параллелепипеда,
построенного на векторах.
Если
векторы
и
заданы координатами в прямоугольной
системе координат
то
можно показать, что

Если
,
то это означает, что параллелепипед на
этих векторах построить нельзя, то есть
векторыи
лежат в одной плоскости, ведь

условие компланарности векторов
и
.
Смешанное
произведение имеет такие свойства:
1)
– операции скалярного и векторного
произведений можно менять местами,
поэтому смешанное произведение записывают
еще в виде;
2)
круговая перестановка множителей не
изменяет величины смешанного произведения
;
3)
перестановка двух соседних множителей
изменяет знак произведения на
противоположный
.
Пример.
Найти объем пирамиды с вершинами
и
Решение
Как
известно из элементарной геометрии,
объем пирамиды
равен
одной шестой объема параллелепипеда,
построенного на векторах
та
.
Поэтому найдем координаты этих векторов
Вычислим
объем параллелепипеда, то есть за
формулой (2.34) найдем смешанное произведение
векторов
и
:
Отсюда
=
84 куб. ед.
Пример
Показать, что точки
и
лежат в одной плоскости.
Решение
Точки
и
будут лежать в одной плоскости, если
векторыи
компланарны. Найдем координаты этих
векторов:Вычислим смешанное произведение этих
векторов
Равенство
нулю смешанного произведения есть
необходимым и достаточным условием
компланарности векторов
и
,
а значит, точкии
принадлежат одной плоскости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
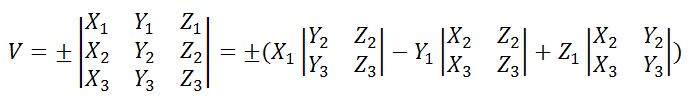
 Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).