Векторная алгебра как найти угол между ребрами – Сайт, где вы сможете решить свои вопросы

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)

Краткая теория

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

найдем как угол
между направляющими векторами

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

и гранью

Для этого вычислим
координаты нормального вектора плоскости

–им будет
векторное произведение векторов

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

. Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

-уравнение
грани

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

из вершины

Нормальный вектор

является
направляющим вектором высоты, кроме того, высота проходит через точку

Искомое уравнение
высоты:

Сделаем схематический чертеж:

Источник

Онлайн калькулятор. Вычисление угла между векторами

Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.

Калькулятор для вычисления угла между векторами

Инструкция использования калькулятора для вычисления угла между векторами

Ввод даных в калькулятор для вычисления угла между векторами

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления угла между векторами

Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Теория. Вычисление угла между векторами

Угол между двумя векторами a и b можно найти использовав следующую формулу:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Скалярное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Угол между векторами

Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

→a * →b = →|a| * →|b| * cosα

Алгебраическая интерпретация.

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

Сначала докажем равенства

для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

Тогда, →AB = →OB – →OA = →b – →a = (bx – ax, by – ay)

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Вспомнив формулу вычисления длины вектора по координатам, получаем

Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.

Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.

Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

В n-мерном пространстве скалярное произведение векторов a = и b = можно найти по формуле:

a * b = a1 * b1 + a2 * b2 + . + an * bn

Свойства скалярного произведения

Свойства скалярного произведения векторов:

Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.

→0 * →0 = 0

Скалярное произведение вектора самого на себя равно квадрату его модуля:

→a * →a = →∣∣a∣∣2

Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:

→a * →b = →b * →a

Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:

(→a + →b) * →c = →a * →c + →b * →c

Сочетательный закон для скалярного произведения:

(k * →a) * →b = k * (→a * →b)

Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

В данном случае:

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Введем систему координат.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).

Найдем координаты векторов →AB1 и →BC1:

Найдем длины векторов →AB1 и →BC1:

Найдем скалярное произведение векторов →AB1 и →BC1:

Найдем косинус угла между прямыми AB1 и BC1:

Пример 5.

а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)

Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.

Обратите внимание на два существенных момента:

В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.

По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Найдём сам угол:

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

Нахождение угла между векторами: онлайн калькулятор

Два вектора всегда образуют угол. Чтобы найти угол между двумя векторами на плоскости или в пространстве, нужно использовать формулу для скалярного произведения и знать длины векторов. Сначала вычисляется косинус угла между векторами, затем находится и сам угол.

Чтобы найти угол между векторами онлайн, не нужно самостоятельно производить громоздкие вычисления. Достаточно просто задать два вектора в удобной форме (точки или координаты) и нажать кнопку «рассчитать».

Как найти угол между векторами с помощью онлайн-калькулятора

Для нахождения угла между векторами с помощью нашего онлайн-калькулятора выполните несколько простых действий:

Укажите размерность векторов. Это может быть плоскость или пространство.
Определитесь с формой представления векторов. Их можно задать координатами либо точками:
В соответствующие поля введите значения векторов и нажмите «Рассчитать».
Рассмотрим наглядный пример с произвольными значениями. Пусть у нас есть два вектора на плоскости, заданные координатами:
После того, как мы нажмем «Рассчитать», калькулятор выдаст решение с пояснением:

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/skalyarnoe-proizvedenie-vektorov

http://zaochnik.com/online-calculators/operacii-nad-vektorami/ugol-mezhdu-vektorami/

[/spoiler]

Источник

Вычисление длины вектора и угла между векторами

Из
свойства 1
,
в координатах по формуле (8.3):

(8.4)

Пусть
длины векторов:
,
,
Из
определения и формул (8.3)-(8.4) следует,
что
угол между векторами вычисляется по
формуле:

=. (8.5)

Пример 1.
Вычислим косинус угла между ребрами АВ
и СD тетраэдра
DАВС,
если А(1;2;1),
В(4;1;2),
С(1;5;3),
D(2;3;1).

.
Найдем координаты векторов

и
:

(4–1;1–2;2–1),
(2–1;3–5;1–3),
тогда
(3;–1;1),
(1;–2;–2).

Подставим в формулу
и вычислим:

,
0,3015
(т.е. 72^о).

Определение
26.

Ортом
вектора

называется вектор
,
который имеет единичную длину и то же
направление, что и вектор
.

(8.6)

Процесс получения
орта вектора называется нормированием.

Если координаты
,
то координаты соответствующего вектору
орта, т.е. нормированного вектора,

. (8.7)

Направление
вектора определяется углами α,
β,
γ,
образованными вектором с осями координат
Ox,
Oy,
Oz.

Определение
27.

Косинусы
углов α,
β,
γ,
образованных векторов с осями координат
Ox,
Oy,
Oz,
называются направляющими
косинусами вектора
и вычисляются по формулам:

,
,
. (8.8)

Тогда
координаты нормированного вектора по
(8.8) в V₃
будут:

Направляющие
косинусы вектора связаны соотношением

Для V₂:

с соотношением:
.

14. Ориентация пространства. Правая и левая тройки веторов

Рассмотрим двумерное
векторное пространство V₂.
Выделим в нем два подпространства:
положительно ориентированное (против
часовой стрелки) и отрицательно
ориентированное (по часовой стрелке).
Подпространство, в котором выбрана
положительная ориентация, назовем
просто ориентированным.

Рассмотрим
трехмерное векторное пространство V₃.
По аналогии с ориентацией плоскости
выделим в нем два подпространства:
положительно ориентированное и
отрицательно ориентированное. Положительно
ориентированный в нем базис назовем
правым,
отрицательно ориентированный
соответственно – левым.

Рассмотрим три
некомпланарных вектора
,,
(порядок определен строго).

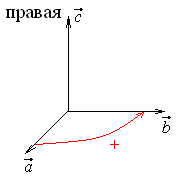
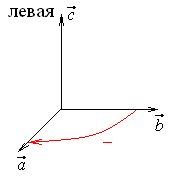
Определение
28.

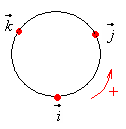
Три
вектора
,,
образуют правую
тройку,
если с конца третьего вектора кратчайший
поворот от первого вектора ко второму
совершается против часовой стрелки.

Примеры.

1)
,, 2)
,,
3)
,,

15. Векторное произведение: определение, свойства

Определение
29.

Векторным
произведением

векторов

и

называется вектор
,
удовлетворяющий условиям:

1)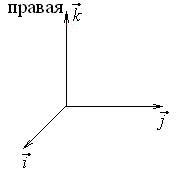
;
(8.9)

2)

и
;

3)
,,
– правая тройка.

Обозначается

или
.

Из определения
следует:
.

Вычислим векторные
произведения ортов.

Покажем, что
.

1)
;

2)

и
;

3)
,
,

– правая тройка.

Покажите
самостоятельно, что
,
,

и т.д. Заполните таблицу:

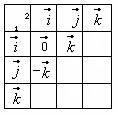
Эти произведения
легко заполнить с помощью схемы Гамильтона
(рис. справа).

Свойства векторного произведения

1.
Антикоммутативность:
=–.

2.
Ассоциативность относительно умножения
на число:

3.
Два ненулевых вектора

и

коллинеарны тогда и только тогда, когда
их векторное произведение равно нулевому
вектору:

Следствие.

(см. также таблицу произведения ортов
).

4. Условие
коллинеарности двух векторов:
=.

5. Дистрибутивность:

(справа),

(слева).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Любой вектор в декартовой системе координат может быть представлен в виде

Где координаты вектора Орты координатных осей.

Вектор с началом в точке и концом в точке Имеет вид:

то есть .

Длина отрезка называется Длиной (модулем) вектора, обозначается = и вычисляется по формуле

Сумма векторов и определяется формулой

Произведение вектора На число определяется формулой

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т. е.

Скалярное произведение векторов и вычисляется по формуле:

Векторным произведением векторов и называется вектор, обозначаемый и удовлетворяющий следующим условиям:

1) длина вектора равна площади параллелограмма, построенного на векторах и , т. е. ;

2) вектор перпендикулярен векторам и ;

3) векторы образуют правую тройку, то есть они ориентированы по отношению друг к другу соответственно как орты .

Модуль векторного произведения векторов и численно равен площади параллелограмма, построенного на этих векторах:

Векторное произведение векторов и вычисляется по формуле:

Смешанным произведением векторов называется скалярное произведение вектора на вектор , то есть .

Модуль смешанного произведения векторов численно равен объему параллелепипеда, построенного на этих векторах:

Пусть Тогда

Уравнение любой плоскости может быть записано в виде:

где .

Вектор , перпендикулярный плоскости, называется Нормальным Вектором плоскости.

Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид

Угол между плоскостями и определяется следующим образом:

Расстояние от точки До плоскости, определяемой уравнением , находится по формуле

Прямая В пространстве может быть задана уравнениями двух плоскостей

Пересекающихся по этой прямой, или Каноническими уравнениями прямой

Которые определяют прямую, проходящую через точку и параллельную вектору . Вектор называется Направляющим вектором прямой.

Уравнения прямой, проходящей через две точки и , имеют вид:

Угол между Двумя прямыми и определяется следующим образом:

Угол между прямой и плоскостью определяется следующим образом:

Если Точка Делит отрезок АВ, где ,, в Отношении, то координаты точки М определяются по формулам:

Задание 1. Даны координаты вершин пирамиды : , . Найти: 1) длину ребра ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды; 6) уравнения прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

Решение. 1) Для определения длины ребра найдем координаты вектора : . Тогда длина ребра будет равна длине вектора :

2) Найдем угол между ребрами и . Для этого, как и раньше, найдем координаты вектора , определяющего ребро . Получим и .

Тогда угол между ребрами и можно найти из определения скалярного произведения двух векторов:

Следовательно, .

3) Чтобы найти угол между ребром и гранью , определим нормальный вектор Плоскости . Из определения векторного произведения двух векторов имеем:

Т. е. и . Тогда , .

Так как нормальный вектор перпендикулярен плоскости , то угол между ребром и гранью определяется как .

4) Площадь грани можем найти по формуле . Следовательно, Кв. ед.

5) Объем пирамиды, построенной на векторах, равен 1/6 объема параллелепипеда, построенного на этих же векторах. Для определения объема параллелепипеда воспользуемся свойством смешанного произведения векторов. В результате имеем:

Таким образом, куб. ед.