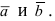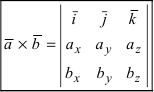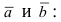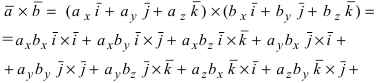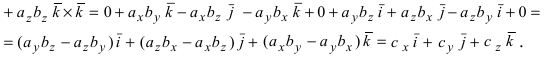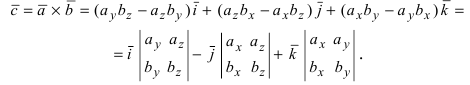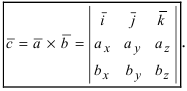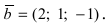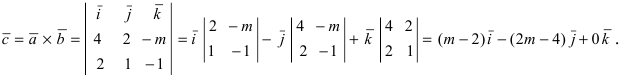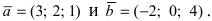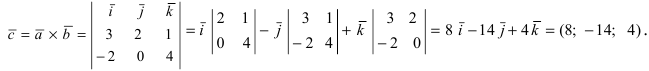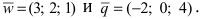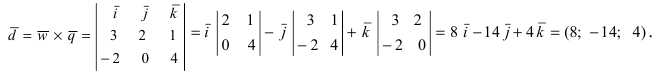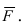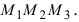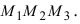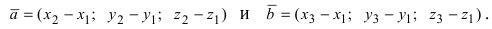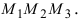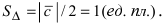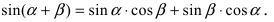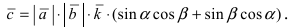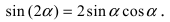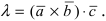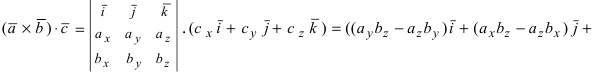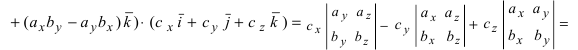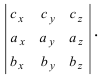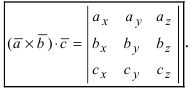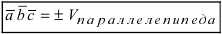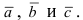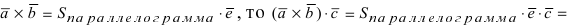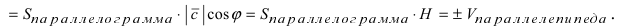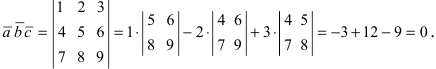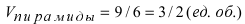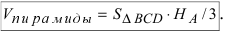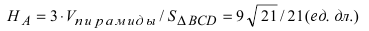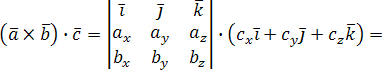Векторное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
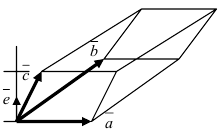
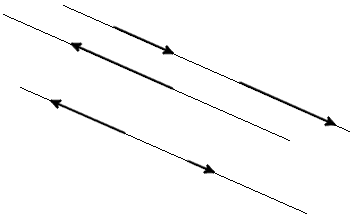
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
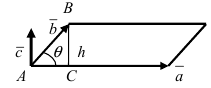
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
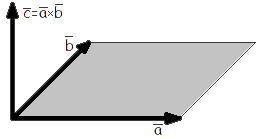
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
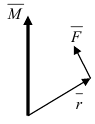
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Длина вектора — основные формулы
Время чтения: 16 минут
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать 
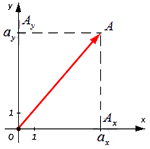
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор 

На взятой системе координат, от её начала отложим вектор
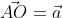
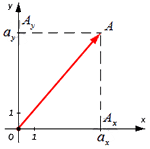
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 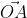
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
Когда вектор 
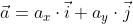


Чтобы рассчитать длину 
Чтобы найти модуль вектора используем ранее приведённую формулу
Ответ:
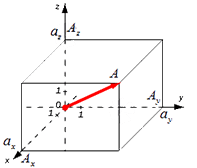
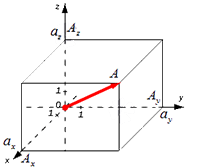
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор 

В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA

Ответ:
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор 
При этом формула вычисления длины вектора 
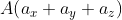
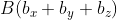
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
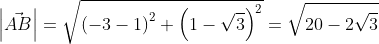
Существует второй вариант решения, где формулы применяются по очереди:
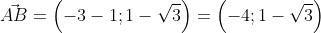
Ответ:
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула для трёхмерного пространства;
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
Нахождение длины вектора, примеры и решения
Длина вектора – основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –
Ответ: A B → = 20 – 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
[spoiler title=”источники:”]
http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html
http://zaochnik.com/spravochnik/matematika/vektory/dlina_vectora/
[/spoiler]
Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 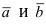
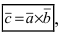
- по модулю численно равен площади параллелограмма, построенного на векторах
- перпендикулярен плоскости, в которой лежат вектора
- тройка векторов
является правой.
Замечание: Из определения векторного произведения следует, что направление вектора 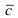
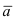
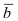
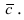
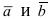
Рис. 14. Площадь параллелограмма, определяющего длину вектора 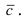
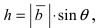
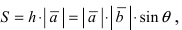
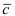
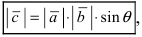
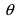
Векторное произведение векторов обладает следующими свойствами:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 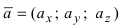
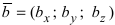
Доказательство: Запишем вектора 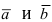
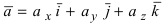
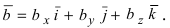
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что 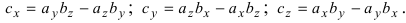
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 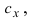
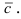
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор 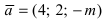
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор 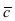
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
1. Физика. Пусть точка начала вектора 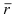
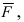
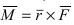
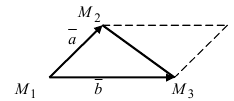
2. Геометрия. Пусть даны три разные точки 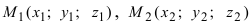
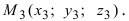
Введем в рассмотрение вектора 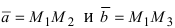
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 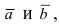
Пример:
Даны три точки 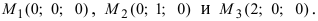
Решение:
Введем в рассмотрение вектора 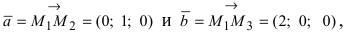
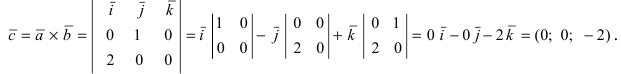
3. Тригонометрия. Выведем формулу для
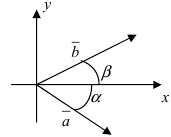
Пусть в плоской декартовой системе координат даны векторы 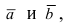
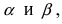
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 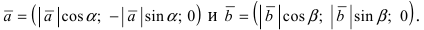
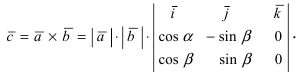
Длина этого вектора равна 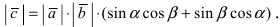
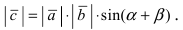
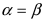
Смешанное произведение векторов
Определение: Смешанным произведением векторов 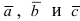
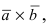
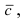
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 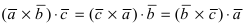
2. Смешанное произведение векторов 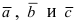
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора 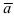
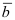
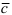
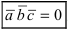
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 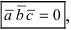
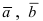
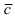
Пример:
Доказать, что вектора 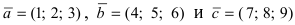
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки 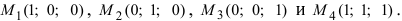
Решение:
Составим векторы 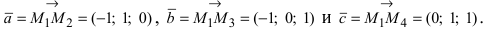
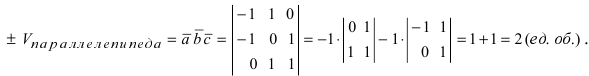
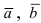
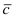
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 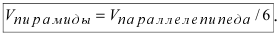
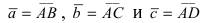
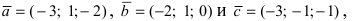
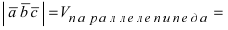
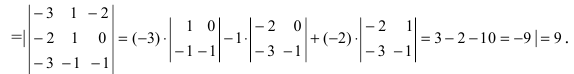
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: 
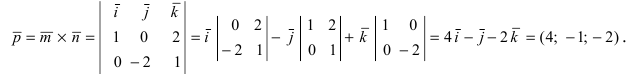
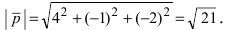
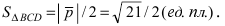
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Матричный метод
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
Калькулятор онлайн.
Вычисление площади треугольника построенного на векторах.
Этот калькулятор онлайн вычисляет площадь треугольника построенного на векторах. Треугольник может быть задан координатами двух векторов или
координатами трех вершин треугольника.
Онлайн калькулятор для вычисления площади треугольника построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Определение векторного произведения векторов
Определение
Векторы ( vec{a}, ; vec{b} ) и ( vec{c} ) называются компланарными, если они лежат в одной плоскости
или параллельных плоскостях.
Определение
Тройка векторов называется упорядоченной, если указано, какой из них считается первым, вторым и третьим.
Например, в записи ( ( vec{a} ; vec{b} ; vec{c} ) ) вектор ( vec{a} ) считается первым, ( vec{b} )
– вторым, ( vec{c} ) – третьим.
Определение
Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу из конца третьего
вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка векторов
называется левой.
Определение
Векторным произведением вектора ( vec{a} ) на вектор ( vec{b} ) называется вектор
( vec{a} times vec{b} ), который определяется тремя условиями:
1) длина вектора ( vec{a} times vec{b} ) равна ( |vec{a}| |vec{b}| sin varphi ), где ( varphi )
– угол между векторами ( vec{a} ) и ( vec{b} )
2) вектор ( vec{a} times vec{b} ) перпендикулярен каждому из векторов ( vec{a} ) и ( vec{b} )
3) векторы ( vec{a}, ;; vec{b}, ;; vec{a} times vec{b} ) образуют правую тройку векторов
Заметим, что условия 2 и 3 относятся к случаю, когда ( |vec{a}| |vec{b}| sin varphi neq 0 ), т.е. вектор
( vec{a} times vec{b} neq vec{0} ). Если же ( |vec{a}| |vec{b}| sin varphi = 0 ), то векторное произведение
определяется только условием 1: в этом случае ( vec{a} times vec{b} = 0 )
Основные свойства векторного произведения векторов
1. Если ( vec{a} ) и ( vec{b} ) – коллинеарные векторы, то ( vec{a} times vec{b} = 0 )
2. Длина векторного произведения неколлинеарных векторов ( vec{a} ) и ( vec{b} ) равна площади параллелограмма,
построенного на этих векторах.
3. ( vec{a} times vec{b} = – vec{b} times vec{a} ) свойство антиперестановочности сомножителей
4. ( ( alpha vec{a} ) times vec{b} = alpha ( vec{b} times vec{a} ) ) свойство сочетательности по отношению к
скалярному произведению
5. ( ( vec{a}+vec{b} ) times vec{c} = vec{a} times vec{c} + vec{b} times vec{c} ) свойство распределительности
относительно суммы векторов.
Выражение векторного произведения через координаты векторов
Теорема
Если векторы ( vec{a} ) и ( vec{b} ) заданы своими координатами:
( vec{a} left( a_x; a_y; a_z right), ;; vec{b} left( b_x; b_y; b_z right) ), то векторное произведение
векторов вычисляется по формуле:
( vec{a} times vec{b} = left( a_y b_z – b_y a_z ; ; ; a_z b_x – b_z a_x ; ; ; a_x b_y – b_x a_y right) )
Эту формулу с помощью определителей второго порядка можно записать в виде
( vec{a} times vec{b} = left( begin{vmatrix} a_y & a_z \ b_y & b_z end{vmatrix} ; ; ;
begin{vmatrix} a_z & a_x \ b_z & b_x end{vmatrix} ; ; ; begin{vmatrix} a_x & a_y \ b_x & b_y end{vmatrix} right) )
Использование векторного произведения
ВЕКТОРОВ
для вычисления площади
некоторых геометрических фигур
Исследовательская работа по математике
Ученика 10 Б класса
МОУ СОШ №73
Перевозникова Михаила
Руководители:
Учитель математики МОУ
СОШ№73 Драгунова Светлана Николаевна
Ассистент каф. математического анализа
механико-математического факультета СГУ им. Н.Г. Чернышевского Бердников Глеб
Сергеевич
Саратов, 2015
Содержание
Введение.
1. Теоретический обзор.
1.1. Векторы и вычисления с векторами.
1.2. Использование скалярного произведения векторов в решении задач
1.3 Скалярное произведение векторов в координатах
1.4. Векторное произведение векторов в трёхмерном Евклидовом
пространстве: определение понятия.
1.5. Координаты векторного произведения векторов.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и
параллелограмма. Выведение формулы и геометрический смысл векторного
произведения векторов.
2.2. Зная только координаты точек, найти площадь треугольника. Доказательство
теоремы
2.3. Проверка на примерах правильности
формулы.
2.4. Практическое
использование векторной алгебры и произведения векторов.
Заключение
Введение
Как известно, многие геометрические задачи имеют два ключевых способа
решения – графический и аналитический. Графический метод связан с
построением графиков и чертежей, а аналитический ‑ предполагает
решение задач преимущественно с помощью алгебраических действий. В последнем
случае алгоритм решений задач связан с аналитической геометрией. Аналитическая
геометрия – это область математики, а точнее линейной алгебры, которая
рассматривает решение геометрических задач средствами алгебры на основе метода
координат на плоскости и в пространстве. Аналитическая геометрия позволяет
анализировать геометрические образы, исследовать линии и поверхности, важные
для практических приложений. При этом в этой науке для расширения
пространственного понимания фигур помимо скалярного произведения векторов
иногда применяется векторное произведение векторов.
В связи с широким распространением трехмерных пространственных
технологий, изучение свойств некоторых геометрических фигур с использованием
векторного произведения представляется актуальным.
В связи с этим была обозначена цель данного проекта –
использование векторного произведения векторов для вычисления площади некоторых
геометрических фигур.
В связи с поставленной целью решались следующие задачи:
1. Теоретически изучить необходимые основы векторной алгебры и дать
определение векторному произведению векторов в системе координат;
2. Проанализировать наличие связи векторного произведения с площадью
треугольника и параллелограмма;
3. Вывести формулу площади треугольника и параллелограмма в
координатах;
4. Проверить на конкретных примерах верность выведенной формулы.
1. Теоретический обзор.
1.1. Векторы и вычисления с векторами
Вектором называется направленный отрезок, для которого
указано его начало и конец:
В данном случае началом отрезка является точка А, концом отрезка
– точка В. Сам вектор обозначен через или
. Чтобы найти координаты вектора
,
зная координаты его начальной точек А и конечной точки В, необходимо из
координат конечной точки вычесть соответствующие координаты начальной точки:
= {Bx –
Ax ; By – Ay}
Коллинеарными называются векторы, лежащие на параллельных прямых или на
одной прямой. При этом вектор ‑ отрезок, характеризующийся длиной и
направлением.
Длина направленного отрезка определяет числовое значение вектора и
называется длиной вектора или модулем вектора.
Длина вектора || в прямоугольных декартовых координатах равна
квадратному корню из суммы квадратов его координат.
С векторами можно совершать различные действия.
Например, сложение. Чтобы их сложить, нужно провести сначала второй
вектор из конца первого, а потом соединить начало первого с концом второго
(рис. 1). Суммой векторов является другой вектор с новыми координатами.
Сумму векторов = {ax ; ay}
и = {bx ; by} можно найти
воспользовавшись следующей формулой:
+
=
{ax + bx; ay + by}

Рис. 1. Действия с векторами
Вычитая векторы, нужно сначала провести их из одной точки, а потом
соединить конец второго с концом первого.
Разность векторов = {ax ; ay}
и = {bx ; by}
можно найти по формуле:
–
=
{ax – bx; ay – by}
Также, векторы можно умножать на число. Результатом также будет вектор,
который в k раз больше (или меньше) данного. Его направление будет зависеть от
знака k: при положительном k векторы сонаправлены, а при отрицательном –
противоположно направлены.
Произведение вектора = {ax ; ay}
и числа k можно найти воспользовавшись следующей формулой:
k · =
{k · ax; k · ay}
А можно ли умножать вектор на вектор?
Конечно, и даже двумя вариантами!
Первый вариант
– скалярное произведение.
Рис. 2. Скалярное произведение в координатах
Для нахождения произведения векторов
можно использовать угол a между данными векторами, показанный на рисунке 3.
Из формулы следует, что скалярное
произведение равно произведению длин данных векторов на косинус угла между
ними, его результатом является число. Важно, что если векторы перпендикулярны,
то их скалярное произведение равно нулю, т.к. косинус прямого угла между ними
равен нулю.
В координатной
плоскости вектор также имеет координаты. Вектора, их координаты и скалярное
произведение являются одними из самых удобных методов вычисления угла между
прямыми (или их отрезками), если введена система координат. И если координаты ,
то их скалярное произведение равно:
В трехмерном пространстве существует
3 оси и, соответственно, у точек и векторов в такой системе будет по 3
координаты, а скалярное произведение векторов вычисляется по формуле:
.
1.2. Векторное произведение векторов в трехмерном
пространстве.
Вторым вариантом вычисления
произведения векторов является векторное произведение. Но, чтобы его определить
требуется уже не плоскость, а трехмерное пространство, в котором начало и конец
вектора имеют по 3 координаты.
В отличие от скалярного произведения
векторов в трёхмерном пространстве операция «векторное умножение» над векторами
приводит к иному результату. Если в предыдущем случае скалярного умножения двух
векторов результатом было число, то в случае векторного умножения векторов
результатом будет другой вектор, перпендикулярный обоим вступившим в
произведение векторам. Поэтому это произведение векторов называется векторным.
Очевидно, что при построении
результирующего вектора , перпендикулярного двум, вступившим в произведение
– и
, может быть выбрано два противоположных
направления. При этом направление результирующего вектора определяется по правилу
правой руки, или правилу буравчика. Если нарисовать векторы так, чтобы их начала совпадали и вращать первый
вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре
пальца правой руки показывали направление вращения (как бы охватывая
вращающийся цилиндр), то оттопыренный большой палец покажет направление
вектора-произведения (рис. 7).
Рис. 7. Правило правой руки
1.3. Свойства векторного
произведения векторов.
Длина
результирующего вектора определяется по формуле
.
При этом ‑
векторное произведение. Как было сказано выше, результирующий вектор будет
перпендикулярен , а его направление
определяется по правилу правой руки.
Векторное произведение зависит от порядка
сомножителей, именно:
.
Векторное
произведение ненулевых векторов равно 0, если они коллинеарны, тогда синус угла
между ними будет равен 0.
Координаты векторов
в трехмерном пространстве выражаются следующим образом: . Тогда координаты результирующего вектора
находим по формуле
.
Длина результирующего вектора находится по
формуле:
.

2. Практическая часть.
2.1. Связь векторного произведения с площадью
треугольника и параллелограмма в плоскости. Геометрический смысл векторного
произведения векторов.
Пусть нам дан
треугольник ABC (рис. 8).
Известно, что .
Если представить стороны треугольника АВ и АС в виде двух
векторов, то в формуле площади треугольника мы находим выражение векторного
произведения векторов:
Из выше сказанного можно определить
геометрический смысл векторного произведения (рис. 9):
длина векторного произведения векторов равна удвоенной
площади треугольника, имеющего сторонами векторы и
, если их отложить
от одной точки.
Другими словами, длина векторного произведения векторов и
равна
площади параллелограмма, построенного на векторах и
, со
сторонами и
и углом между ними,
равным 
.
Рис.
9. Геометрический смысл векторного произведения векторов
В связи с этим, можно
привести еще одно определение векторного произведения векторов:
Векторным произведением вектора на
вектор называется вектор
, длина которого численно равна площади
параллелограмма построенного на векторах и
, перпендикулярный к плоскости этих
векторов и направленный так, чтоб наименьшее вращение от к
вокруг
вектора осуществлялось против часовой
стрелки, если смотреть с конца вектора (рис.
10).
Рис. 10. Определение векторного произведения векторов
с использованием параллелограмма
2.2. Вывод формулы для нахождения площади треугольника
в координатах.
Итак, нам дан
треугольник АВС в плоскости и координаты его вершин. Найдем площадь этого
треугольника (рис. 11).
Рис. 11. Пример
решения задачи на нахождение площади треугольника по координатам его вершин
Решение.
Для начала,
рассмотрим координаты вершин в пространстве и вычислим координаты векторов АВ и
АС.
По данной прежде
формуле подсчитаем координаты их векторного произведения. Длина этого вектора
равна 2 площадям треугольника АВС. Площадь треугольника равна 10.
Более того, если
мы рассмотрим треугольник на плоскости, то первые 2 координаты векторного
произведения всегда будут равны нулю, поэтому мы можем сформулировать следующую
теорему.
Теорема: Пусть
дан треугольник АВС и координаты его вершин (рис.
12).
Тогда .

Доказательство теоремы
Доказательство.
Рассмотрим точки
в пространстве и вычислим координаты векторов ВС и ВА. . По приведенной раньше формуле вычислим
координаты векторного произведения этих векторов. Обратим внимание, что все
члены, содержащие z1 или z2, равны 0, т.к. z1и z2 = 0. УБРАТЬ!!!
Итак,
следовательно,
2.3. Проверка правильности формулы на примерах
Найти площадь
треугольника образованного векторами a = {-1; 2; -2}
и b = {2; 1; -1}.
Решение: Найдем
векторное произведение этих векторов:
|
a × b= |
i |
j |
k |
= |
|
-1 |
2 |
-2 |
||
|
2 |
1 |
-1 |
= i(2 · (-1) – (-2) · 1) – j((-1) · (-1) – (-2) · 2) + k((-1) · 1 – 2 · 2) =
=
i(-2 + 2) – j(1 + 4) + k(-1 – 4) =
-5j – 5k = {0; -5; -5}
Из свойств векторного произведения:
|
SΔ = |
1 |
|a × b| = |
1 |
√02 + 52 + 52 = |
1 |
√25 + 25 = |
1 |
√50 = |
5√2 |
|
2 |
2 |
2 |
2 |
2 |
Ответ: SΔ = 2.5√2.
Заключение
2.4. Приложения векторной алгебры
и скалярного и векторного произведения векторов.
Где же нужны векторы? Векторное
пространство и векторы носят не только теоретический характер, но и имеют
вполне реальное практическое применение в современном мире.
В механике и физике многие величины
имеют не только численное значение, но и направление. Такие величины называются
векторными. Вместе с использованием элементарных механических понятий,
опираясь на их физический смысл, многие величины рассматриваются как скользящие
векторы, а их свойства описываются как аксиомами, как это принято в
теоретической механике, так и при помощи математических свойств векторов.
Наиболее яркими примерами векторных величин являются скорость, импульс и сила
(рис. 12). Например, момент импульса и сила Лоренца математически записываются
с помощью векторов.
В физике важны не только сами вектора,
но в большой степени важны и их произведения, которые помогают вычислять
некоторые величины. Векторное произведение полезно для определения
коллинеарности векторов ‑ модуль векторного произведения двух векторов равен
произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если
векторы сонаправленны или противоположно направленны.
Еще один пример: скалярное
произведение используется для вычисления работы по приведенной ниже формуле,
где F – вектор силы, а s – вектор перемещения.
Одним из примеров использования
произведения векторов является момент силы, равный произведению радиус-вектора,
проведенного от оси вращения к точке приложения силы, на вектор этой силы.
Многое
из того, что вычисляется в физике по правилу правой руки является векторным
произведением. Найти подтверждения, привести примеры.
Стоит
еще заметить, что двухмерным и трехмерным пространством не исчерпываются
возможные варианты векторных пространств. Высшая математика рассматривает
пространства большей размерности, в которых также определяются аналоги формул
для скалярного и векторного произведения. Несмотря на то, что пространства
большей размерности, чем 3, человеческое сознание неспособно представить
визуально, они удивительным образом находят себе приложения во многих областях
науки и промышленности.
В то же время результатом
векторного произведения векторов в трёхмерном Евклидовом пространстве является
не число, а результирующий вектор со своими координатами, направлением и
длиной.
Направление результирующего
вектора определяется по правилу правой руки, что является одним из самых
удивительных положений аналитической геометрии.
Векторное произведение векторов
может быть использовано в нахождении площади треугольника или параллелограмма
по заданным координатам вершин, что было подтверждено выведением формулы,
доказательством теоремы и решением практических задач.
Векторы широко используются в
физике, где такие показатели как скорость, импульс и сила могут быть
представлены в виде векторных величин и вычисляются геометрически.
Список использованных источников
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б.
и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: Просвещение, 2013. 383 с.
Атанасян Л.С., Бутузов В. Ф., Кадомцев С. Б. и
др. Геометрия. 10-11 классы: учебник для общеобразовательных организаций:
базовый и профильный уровни. М.: Просвещение, 2013. 255 с.
Бугров Я.С., Никольский С.М. Высшая
математика. Том первый: элементы линейной алгебры и аналитической геометрии.
????Клетеник Д.В. Сборник задач по
аналитической геометрии. М.: Наука, Физматлит, 1998.
Аналитическая геометрия.
http://a-geometry.narod.ru/problems/problems_32.htm
Математика. Клевер.
http://www.cleverstudents.ru/vectors/vector_product_of_vectors.html
—–Изучение математики онлайн.
http://ru.onlinemschool.com/math/library/vector/multiply1/
Сайт В. Глазнева.
http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm
——Википедия.
https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED%E8%E5
Векторным
произведениемвектора a на вектор b
называется вектор c, длина которого
численно равна площади параллелограмма
построенного на векторах a и b,
перпендикулярный к плоскости этих
векторов и направленный так, чтоб
наименьшее вращение от a к b вокруг
вектора c осуществлялось против часовой
стрелки, если смотреть с конца вектора
c (рис. 1).
|
|
|
рис. 1 |
Формулы
вычисления векторного произведения
векторов
Векторное
произведениедвух векторов a = {ax;
ay; az} и b = {bx; by;
bz} в декартовой системе координат
– это вектор, значение которого можно
вычислить, используя следующие формулы:
|
a × b = |
i |
j |
k |
= i(aybz |
|
ax |
ay |
az |
||
|
bx |
by |
bz |
a × b = {aybz– azby; azbx– axbz;
axby– aybx}
Свойства
векторного произведения векторов
-
Геометрический смысл векторного
произведения.
Модуль векторного произведения двух
векторов a и b равен площади параллелограмма
построенного на этих векторах:
Sпарал= a × b]
-
Геометрический смысл векторного
произведения.
Площадь треугольника построенного на
векторах a и b равна половине модуля
векторного произведения этих векторов:
|
SΔ = |
1 |
|a × b| |
|
2 |
-
Векторное произведения двух не нулевых
векторов a и b равно нулю тогда и только
тогда, когда вектора
коллинеарны. -
Вектор c, равный векторному произведению
не нулевых векторов a и b, перпендикулярен
этим векторам. -
a × b = -b × a
-
(k a) × b = a × (k b) = k (a × b)
-
(a + b) × c = a × c + b × c
14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
Смешанным
произведением
некомпланарныхвекторов
,взятых в данном порядке, называетсяобъём параллелепипеда, построенного
на данных векторах, снабжённый знаком
«+», если базисправый,
и знаком «–», если базислевый.
1.
Смешанное
произведение не меняется при циклической
перестановке его сомножителей (не
меняется ни объем параллелепипеда, ни
ориентация его ребер):
.
2.
Смешанное
произведение не меняетсязнаков
векторного и скалярного умножения:,
поэтому смешанное произведение записывают.
3.
Смешанное
произведение меняет свой знак при
перемене любых двух вектор-сомножителей:
,
.
4.
Смешанное
произведение ненулевых векторов
,
и
равно
нулю тогда и только тогда, когда они
компланарны:,
,
–
компланарны.
Доказательство.
Предположим, что векторы
,
и
–
не компланарны. Тогда можно построить
параллелепипед имеющий объем,
т.е.,
но это противоречит условию, согласно
которого,.
Следовательно, векторы,
и
–
компланарны.
Обратно,
пусть
,
и
–
компланарны. Тогда вектори
перпендикулярен плоскости, в которой
находятся векторы,
и
,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
напримерЭто
значит, что
.
Смешанное
произведение векторов, заданных своими
проекциями в декартовой системе
координат.
Пусть
векторы заданы своими разложениями по
ортам в декартовой системе координат:
,
и
.
Найдем
их смешанное произведение, используя
выражения в координатах для векторного
и скалярного произведений:
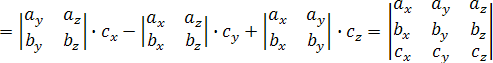
Итак,
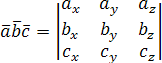
Приложения
смешанного произведения:
1.
Определение
взаимной ориентации векторов в
пространстве.
Если
,
и
–
правая тройка, еслилевая.
2.
Установление
компланарности векторов:
(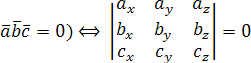
(,
,
–
компланарны).
3.
Определение
объема параллелепипеда и треугольной
пирамиды (тетраэдра):
,
.
Пример.
Компланарны ли векторы
,
и
,
если
.
Решение.
Вычислим смешанное произведение
векторов:
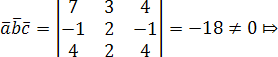
,
и
не
компланарны.
Пример.
Доказать, что векторы
,
и
компланарны.
Решение.
Рассмотрим матрицу, составленную из
координат векторов
,
и
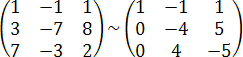
т. к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
Пример.
Вычислить объем тетраэдра с вершинами
в точках
и
его высоту, опущенную из вершинына
грань,
если
Решение.
Найдем координаты векторов:
,
,
.
Вычислим
объем:
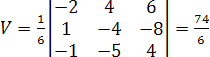
Поскольку
объем тетраэдра
,
то высота.
Вычислим
площадь основания тетраэдра
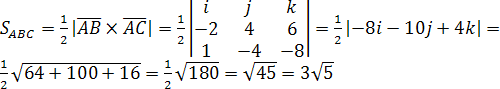
Итак,
высота
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

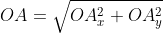
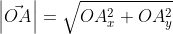
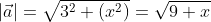
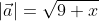
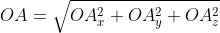
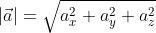
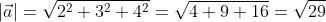
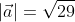
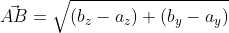
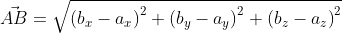
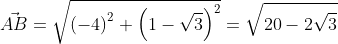
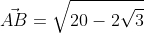
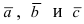
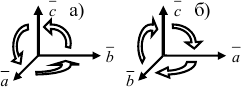
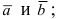
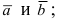
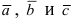 является правой.
является правой.