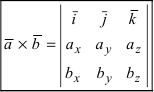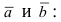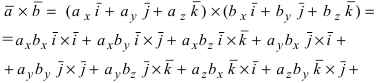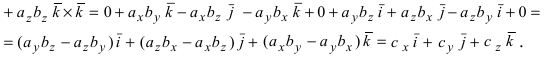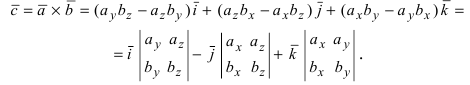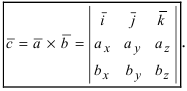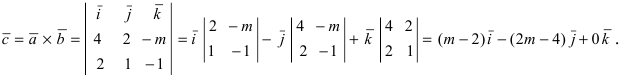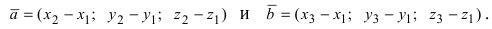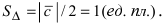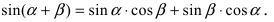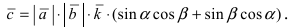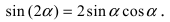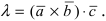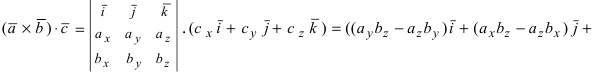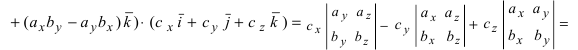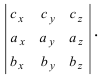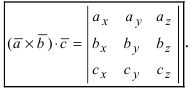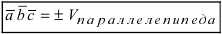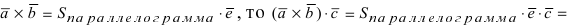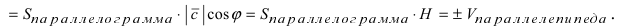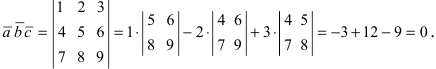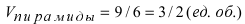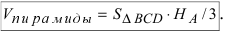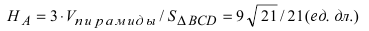Нахождение угла между векторами с помощью скалярного произведения
Косинус угла между векторами a⃗=(a1;a2)vec{a}=(a_{1};a_{2}) и b⃗=(b1;b2)vec{b}=(b_{1};b_{2}) может быть вычислен по формуле
cos(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=a1⋅b1+a2⋅b2a12+a22⋅b12+b22.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}= frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}}{sqrt{a_{1}^{2}+a_{2}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}}}.
Следовательно, угол между векторами a⃗=(a1;a2)vec{a}=(a_{1};a_{2}) и b⃗=(b1;b2)vec{b}=(b_{1};b_{2}) может быть вычислен по формуле
(a⃗,b⃗^)=arccos(a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣)=arccos(a1⋅b1+a2⋅b2a12+a22⋅b12+b22).left(widehat{vec{a},vec{b}}right)=arccosleft(frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}right)=arccosleft(frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}}{sqrt{a_{1}^{2}+a_{2}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}}}right).
Пример 1
Найти угол между векторами a⃗=(1;−1)vec{a}=(1; -1) и b⃗=(1;2).vec{b}=(1; 2).
cos(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=1⋅1+(−1)⋅212+(−1)2⋅12+22=1−22⋅5=−110.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{1cdot1+(-1)cdot2}{sqrt{1^{2}+(-1)^{2}}cdot sqrt{1^{2}+2^{2}}}=frac{1-2}{sqrt{2}cdotsqrt{5}}=frac{-1}{sqrt{10}}.
(a⃗,b⃗^)=arccos(−110)=arccos(−1010).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{-1}{sqrt{10}} right )=arccosleft ( frac{-sqrt{10}}{10} right ).
Ответ: (a⃗,b⃗^)=arccos(−1010).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{-sqrt{10}}{10} right).
Пример 2
Найти угол между векторами a⃗=(2;3)vec{a}=(2; 3) и b⃗=(3;1).vec{b}=(3; 1).
cos(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=2⋅3+3⋅122+32⋅32+12=6+313⋅10=9130=9130130.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{2cdot3+3cdot1}{sqrt{2^{2}+3^{2}}cdot sqrt{3^{2}+1^{2}}}=frac{6+3}{sqrt{13}cdotsqrt{10}}=frac{9}{sqrt{130}}=frac{9sqrt{130}}{130}.
(a⃗,b⃗^)=arccos(9130130).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{9sqrt{130}}{130} right ).
Ответ: (a⃗,b⃗^)=arccos(9130130).left ( widehat{vec{a},vec{b}} right )=arccos left ( frac{9sqrt{130}}{130} right ).
Косинус угла между векторами a⃗=(a1;a2;a3)vec{a}=(a_{1};a_{2};a_{3}) и b⃗=(b1;b2;b3)vec{b}=(b_{1};b_{2};b_{3}) может быть вычислен по формуле
cos(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=a1⋅b1+a2⋅b2+a3⋅b3a12+a22+a32⋅b12+b22+b32.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}= frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}+a_{3}cdot b_{3}}{sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}.
Следовательно, угол между векторами a⃗=(a1;a2;a3)vec{a}=(a_{1};a_{2};a_{3}) и b⃗=(b1;b2;b3)vec{b}=(b_{1};b_{2};b_{3}) может быть вычислен по формуле
(a⃗,b⃗^)=arccos(a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣)=arccos(a1⋅b1+a2⋅b2+a3⋅b3a12+a22+a32⋅b12+b22+b32).left(widehat{vec{a},vec{b}}right)=arccosleft(frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}right)=arccosleft(frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}+a_{3}cdot b_{3}}{sqrt{a_{1}^{2}+a_{2}^{2}+ a_{3}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}+ b_{3}^{2}}}right).
Пример 3
Найти угол между векторами a⃗=(1;2;3)иb⃗=(1;−2;3).vec{a}=(1; 2; 3) и vec{b}=(1; -2; 3).
cos(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=1⋅1+2⋅(−2)+3⋅312+22+32⋅12+(−2)2+32=1−4+914⋅14=614=37.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{1cdot1+2cdot(-2)+3cdot3}{sqrt{1^{2}+2^{2}+3^{2}}cdot sqrt{1^{2}+(-2)^{2}+3^{2}}}=frac{1-4+9}{sqrt{14}cdotsqrt{14}}=frac{6}{14}=frac{3}{7}.
(a⃗,b⃗^)=arccos(37).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{3}{7} right ).
Ответ: (a⃗,b⃗^)=arccos(37).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{3}{7} right ).
Пример 4
Найти угол между векторами a⃗=(2;−1;−2)vec{a}=(2; -1; -2) и b⃗=(1;3;−2).vec{b}=(1; 3; -2).
cos(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=2⋅1+(−1)⋅3+(−2)⋅(−2)22+(−1)2+(−2)2⋅12+32+(−2)2=2−3+49⋅14=33⋅14=114=1414.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{2cdot1+(-1)cdot3+(-2)cdot(-2)}{sqrt{2^{2}+(-1)^{2}+(-2)^{2}}cdot sqrt{1^{2}+3^{2}+(-2)^{2}}}=frac{2-3+4}{sqrt{9}cdotsqrt{14}}=frac{3}{3cdotsqrt{14}}=frac{1}{sqrt{14}}=frac{sqrt{14}}{14}.
(a⃗,b⃗^)=arccos(1414).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{sqrt{14}}{14} right ).
Ответ: (a⃗,b⃗^)=arccos(1414).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{sqrt{14}}{14} right ).
Нахождение угла между векторами с помощью векторного произведения
Синус угла между векторами можно вычислить по формуле: sin(a⃗,b⃗^)=∣a⃗×b⃗∣∣a⃗∣⋅∣b⃗∣.sin(widehat{vec{a},vec{b}})=frac{left | vec{a}times vec{b} right |}{left | vec{a} right |cdotleft | vec{b} right |}.
Пример 1
Найти угол между векторами a⃗=(2;−1;2)vec{a}=(2;-1;2) и b⃗=(3;0;1).vec{b}=(3;0;1).
a⃗×b⃗=∣ijk2−12301∣=(−1−0)i−(2−6)j+(0+3)k=−i+4j+3k.vec{a}times vec{b}=begin{vmatrix}i&j&k\2&-1&2\3&0&1end{vmatrix}=(-1-0)i-(2-6)j+(0+3)k=-i+4j+3k.
∣a⃗×b⃗∣=(−1)2+42+32=1+16+9=26.left | vec{a}times vec{b} right |=sqrt{(-1)^{2}+4^{2}+3^{2}}=sqrt{1+16+9}=sqrt{26}.
∣a⃗∣=22+(−1)2+22=4+1+4=9=3.left | vec{a} right |=sqrt{2^{2}+(-1)^{2}+2^{2}}=sqrt{4+1+4}=sqrt{9}=3.
∣b⃗∣=32+02+12=9+0+1=10.left | vec{b} right |=sqrt{3^{2}+0^{2}+1^{2}}=sqrt{9+0+1}=sqrt{10}.
sin(a⃗,b⃗^)=26310=132325=1335=6515.sin(widehat{vec{a},vec{b}})=frac{sqrt{26}}{3sqrt{10}}=frac{sqrt{13}sqrt{2}}{3sqrt{2}sqrt{5}}=frac{sqrt{13}}{3sqrt{5}}=frac{sqrt{65}}{15}.
(a⃗,b⃗^)=arcsin(6515).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{65}}{15} right ).
Ответ: (a⃗,b⃗^)=arcsin(6515).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{65}}{15} right ).
Пример 2
Найти угол между векторами a⃗=(1;1;3)vec{a}=(1;1;3) и b⃗=(0;1;1).vec{b}=(0;1;1).
a⃗×b⃗=∣ijk113011∣=(1−3)i−(1−0)j+(1−0)k=−2i−j+k.vec{a}times vec{b}=begin{vmatrix}i&j&k\1&1&3\0&1&1end{vmatrix}=(1-3)i-(1-0)j+(1-0)k=-2i-j+k.
∣a⃗×b⃗∣=(−2)2+(−1)2+12=4+1+1=6.left | vec{a}times vec{b} right |=sqrt{(-2)^{2}+(-1)^{2}+1^{2}}=sqrt{4+1+1}=sqrt{6}.
∣a⃗∣=12+12+32=1+1+9=11.left | vec{a} right |=sqrt{1^{2}+1^{2}+3^{2}}=sqrt{1+1+9}=sqrt{11}.
∣b⃗∣=02+12+12=0+1+1=2.left | vec{b} right |=sqrt{0^{2}+1^{2}+1^{2}}=sqrt{0+1+1}=sqrt{2}.
sin(a⃗,b⃗^)=6112=32112=311=3311.sin(widehat{vec{a},vec{b}})=frac{sqrt{6}}{sqrt{11}sqrt{2}}=frac{sqrt{3}sqrt{2}}{sqrt{11}sqrt{2}}=frac{sqrt{3}}{sqrt{11}}=frac{sqrt{33}}{11}.
(a⃗,b⃗^)=arcsin(3311).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{33}}{11} right ).
Ответ: (a⃗,b⃗^)=arcsin(3311).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{33}}{11} right ).
Тест по теме “Как найти угол между двумя векторами”
Марина Николаевна Ковальчук
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Угол между векторами
Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.
Определение 1
Пусть нам даны два вектора $overline{α}$ и $overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline{α}=overline{OA}$ и $overline{β}=overline{OB}$, тогда угол $AOB$ будет носить название угол между двумя векторами. (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $overline{α}$ и $overline{β}$ будут сонаправленными, или один или оба из них будет нулевым вектором, то угол между этими векторами будет равняться $0^circ$.
Обозначение: $∠(overline{α},overline{β})$
Нахождение угла между векторами в пространстве с помощью скалярного произведения
Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.
Определение 2
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$overline{δ}overline{β}=|overline{δ}||overline{β}|cos∠(overline{δ},overline{β})$
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Теорема 1
Скалярное произведение двух данных векторов $overline{δ}$ и $overline{β}$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, равняется сумме произведений их соответствующих координат.
Математически выглядит следующим образом
$overline{δ}cdot overline{β}=δ_1 δ_2+β_1 β_2+γ_1 γ_2$
«Как найти угол между векторами» 👇
Обозначение: $overline{δ}cdot overline{β}$.
С помощью скалярного произведения мы можем найти косинус угла между векторами. Пусть нам даны векторы $overline{δ}$ и $overline{β}$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, соответственно. Из определения 2 получим, что
$cos∠(overline{δ},overline{β})=frac{overline{δ}cdot overline{β}}{|overline{δ}||overline{β}|}$
Из теоремы 1 мы знаем, что $overline{δ}cdot overline{β}=δ_1 δ_2+β_1 β_2+γ_1 γ_2$, следовательно
$cos∠(overline{δ},overline{β})=frac{δ_1 δ_2+β_1 β_2+γ_1 γ_2}{|overline{δ}||overline{β}|}$
Расписывая по формуле длины вектора значения $|overline{δ}|$ и $|overline{β}|$, окончательно получим
$cos∠(overline{δ},overline{β})=frac{δ_1 δ_2+β_1 β_2+γ_1 γ_2}{sqrt{δ_1^2+β_1^2+γ_1^2 } sqrt{δ_2^2+β_2^2+γ_2^2}}$
Найдя значение косинуса, мы легко найдем и значение самого угла.
Пример 1
Найти косинус угла между векторами $overline{δ}$ и $overline{β}$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем скалярное произведение между данными векторами через координаты:
$overline{δ}cdot overline{β}=1cdot 3+(-2)cdot 0+2cdot 4=11$
Найдем длины этих векторов:
$|overline{δ}|=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3$
$|overline{β}|=sqrt{3^2+0^2+4^2}=sqrt{25}=5$
В результате, получим
$cos∠(overline{δ},overline{β})=frac{11}{3cdot 5}=frac{11}{15}$
Ответ: $frac{11}{15}$.
Нахождение угла между векторами с помощью векторного произведения
Вспомним сначала, определение векторного произведения и каким образом его можно находить.
Определение 3
Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Обозначение: $overline{δ}хoverline{β}$.
Математически это выглядит следующим образом:
- $|overline{δ}хoverline{β}|=|overline{δ}||overline{β}|sin∠(overline{δ},overline{β})$
- $overline{δ}хoverline{β}⊥overline{δ}$, $overline{δ}хoverline{β}⊥overline{β}$
- $(overline{δ}хoverline{β},overline{δ},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 2)
Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ
Для нахождения вектора векторного произведения можно пользоваться следующей формулой:
$overline{δ}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\δ_1&δ_2&δ_3\β_1&β_2&β_3end{vmatrix}$
С помощью векторного произведения мы можем найти синус угла между данными векторами. Пусть нам даны векторы $overline{δ}$ и $overline{β}$ с координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$, соответственно. Из определения 3 получим, что
${sin angle left(overrightarrow{delta },overrightarrow{beta }right) }=frac{left|overrightarrow{delta }хoverrightarrow{beta }right|}{left|overrightarrow{delta }right||overrightarrow{beta }|}$
Найдем вектор векторного произведения по формуле:
$overline{δ}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\δ_1&δ_2&δ_3\β_1&β_2&β_3end{vmatrix}=(δ_2 β_3-δ_3 β_2,δ_3 β_1-δ_1 β_3,δ_1 β_2-δ_2 β_1)$
Расписывая по формуле длины вектора значения $|overline{δ}|$, $|overline{β}|$ и $|overline{δ}хoverline{β}|$, окончательно получим
$sin∠(overline{δ},overline{β})=frac{sqrt{(δ_2 β_3-δ_3 β_2)^2+(δ_3 β_1-δ_1 β_3)^2+(δ_1 β_2-δ_2 β_1)^2}}{sqrt{δ_1^2+δ_2^2+δ_3^2}sqrt{β_1^2+β_2^2+β_3^2}}$
Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.
Пример 2
Найти синус угла между векторами $overline{δ}$ и $overline{β}$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем вектор векторного произведения между данными векторами по формуле:
$overline{δ}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\1&-2&2\3&0&4end{vmatrix}=-8overline{i}+2overline{j}+6overline{k}=(-8,1,6)$
Найдем длины этих векторов:
$|overline{δ}хoverline{β}|=sqrt{(-8)^2+2^2+6^2}=sqrt{104}=2sqrt{26}$
$|overline{δ}|=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3$
$|overline{β}|=sqrt{3^2+0^2+4^2}=sqrt{25}=5$
В результате, получим
$sin∠(overline{δ},overline{β})=frac{2sqrt{26}}{3cdot 5}=frac{2sqrt{26}}{15}$
Ответ: $frac{2sqrt{26}}{15}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
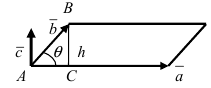
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70
Ответ: a → , b → ^ = – a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,
b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Как найти угол между векторами
Вы будете перенаправлены на Автор24
Угол между векторами
Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.
Пусть нам даны два вектора $overline<α>$ и $overline<β>$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline<α>=overline$ и $overline<β>=overline$, тогда угол $AOB$ будет носить название угол между двумя векторами. (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $overline<α>$ и $overline<β>$ будут сонаправленными, или один или оба из них будет нулевым вектором, то угол между этими векторами будет равняться $0^circ$.
Нахождение угла между векторами в пространстве с помощью скалярного произведения
Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Скалярное произведение двух данных векторов $overline<δ>$ и $overline<β>$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, равняется сумме произведений их соответствующих координат.
Математически выглядит следующим образом
$overline<δ>cdot overline<β>=δ_1 δ_2+β_1 β_2+γ_1 γ_2$
Готовые работы на аналогичную тему
Обозначение: $overline<δ>cdot overline<β>$.
С помощью скалярного произведения мы можем найти косинус угла между векторами. Пусть нам даны векторы $overline<δ>$ и $overline<β>$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, соответственно. Из определения 2 получим, что
Из теоремы 1 мы знаем, что $overline<δ>cdot overline<β>=δ_1 δ_2+β_1 β_2+γ_1 γ_2$, следовательно
Расписывая по формуле длины вектора значения $|overline<δ>|$ и $|overline<β>|$, окончательно получим
Найдя значение косинуса, мы легко найдем и значение самого угла.
Найти косинус угла между векторами $overline<δ>$ и $overline<β>$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем скалярное произведение между данными векторами через координаты:
$overline<δ>cdot overline<β>=1cdot 3+(-2)cdot 0+2cdot 4=11$
Найдем длины этих векторов:
В результате, получим
Нахождение угла между векторами с помощью векторного произведения
Вспомним сначала, определение векторного произведения и каким образом его можно находить.
Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Математически это выглядит следующим образом:
- $|overline<δ>хoverline<β>|=|overline<δ>||overline<β>|sin∠(overline<δ>,overline<β>)$
- $overline<δ>хoverline<β>⊥overline<δ>$, $overline<δ>хoverline<β>⊥overline<β>$
- $(overline<δ>хoverline<β>,overline<δ>,overline<β>)$ и $(overline,overline,overline)$ одинаково ориентированы (рис. 2)
Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ
Для нахождения вектора векторного произведения можно пользоваться следующей формулой:
С помощью векторного произведения мы можем найти синус угла между данными векторами. Пусть нам даны векторы $overline<δ>$ и $overline<β>$ с координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$, соответственно. Из определения 3 получим, что
Найдем вектор векторного произведения по формуле:
$overline<δ>хoverline<β>=beginoverline&overline&overline\δ_1&δ_2&δ_3\β_1&β_2&β_3end=(δ_2 β_3-δ_3 β_2,δ_3 β_1-δ_1 β_3,δ_1 β_2-δ_2 β_1)$
Расписывая по формуле длины вектора значения $|overline<δ>|$, $|overline<β>|$ и $|overline<δ>хoverline<β>|$, окончательно получим
Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.
Найти синус угла между векторами $overline<δ>$ и $overline<β>$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем вектор векторного произведения между данными векторами по формуле:
Найдем длины этих векторов:
В результате, получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 07 2022
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://spravochnick.ru/geometriya/metod_koordinat_v_prostranstve/kak_nayti_ugol_mezhdu_vektorami/
[/spoiler]
Умножаем эти вектора. Их скалярное произведение равно произведению длин этих векторов на косинус угла между ними.
Угол нам неизвестен, зато известны координаты.
Математически запишем это так.
Пусть, даны вектора a{x1;y1} и b{x2;y2}
Тогда
a*b=|a|*|b|*cosA
отсюда
cosA=a*b/|a|*|b|
Рассуждаем.
a*b-скалярное произведение векторов, равно сумме произведений соответствующих координат координат этих векторов, т. е. равно x1*x2+y1*y2
|a|*|b|-произведение длин векторов, равно √((x1)^2+(y1)^2)*√((x2)^2+(y2)^2).
Значит, косинус угла между векторами равен:
cosA=(x1*x2+y1*y2)/√((x1)^2+(y1)^2)*√((x2)^2+(y2)^2)
Зная косинус угла, можем вычислить и его синус. Рассуждаем, как это сделать:
если косинус угла положительный, значит это угол лежит в 1 или 4 четверти, значит его синус либо положительный, либо отрицательный. Но т. к. угол между векторами-меньше или равен 180 градусов, то его синус – положительный. Аналогично рассуждаем, если косинус – отрицательный.
sinA=√(1-cos^2A)=√(1-((x1*x2+y1*y2)/√((x1)^2+(y1)^2)*√((x2)^2+(y2)^2))^2)
вот так))) ) удачи разобраться)))
Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 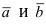
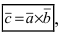
- по модулю численно равен площади параллелограмма, построенного на векторах
- перпендикулярен плоскости, в которой лежат вектора
- тройка векторов
является правой.
Замечание: Из определения векторного произведения следует, что направление вектора 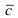
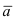
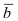
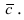
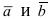
Рис. 14. Площадь параллелограмма, определяющего длину вектора 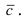
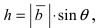
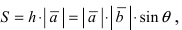
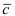
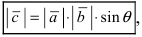
Векторное произведение векторов обладает следующими свойствами:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 
Доказательство: Запишем вектора 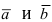
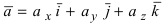
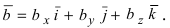
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что 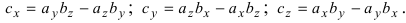
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 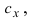
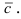
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор 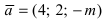
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор 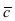
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
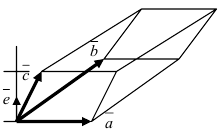
1. Физика. Пусть точка начала вектора 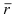
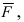
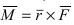
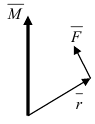
2. Геометрия. Пусть даны три разные точки 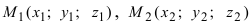
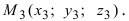
Введем в рассмотрение вектора 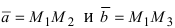
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 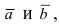
Пример:
Даны три точки 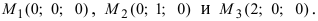
Решение:
Введем в рассмотрение вектора 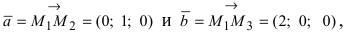
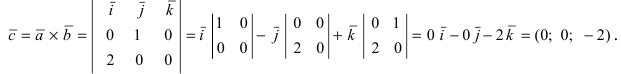
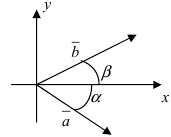
3. Тригонометрия. Выведем формулу для
Пусть в плоской декартовой системе координат даны векторы 
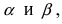
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 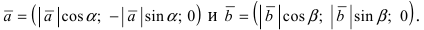
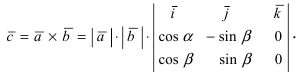
Длина этого вектора равна 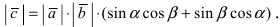
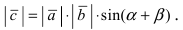
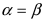
Смешанное произведение векторов
Определение: Смешанным произведением векторов 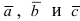
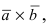
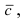
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 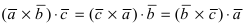
2. Смешанное произведение векторов 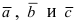
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора 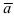
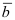
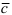
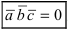
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 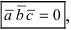
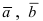
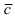
Пример:
Доказать, что вектора 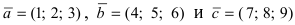
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки 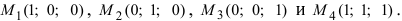
Решение:
Составим векторы 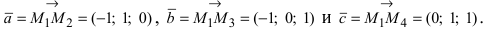
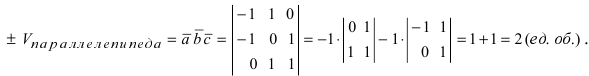
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 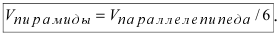
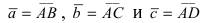
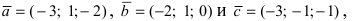
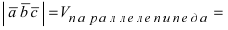
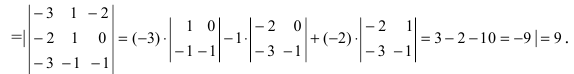
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: 
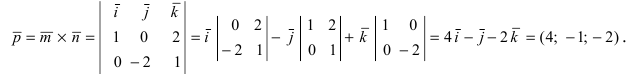
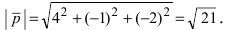
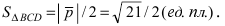
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Матричный метод
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства




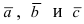
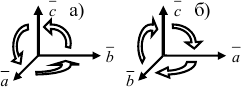
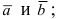
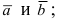
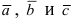 является правой.
является правой.