Содержание
- Уравнение прямой на плоскости
- Уравнения прямой на плоскости в координатной форме
- Общее уравнение прямой
- Параметрическое уравнение прямой
- Параметрическое уравнение прямой в канонической форме
- Уравнение прямой, проходящей через две точки
- Уравнения прямой на плоскости в векторной форме
- Векторное уравнение прямой в параметрической форме
- Нормальное векторное уравнение прямой
- Векторное уравнение прямой, проходящей через две точки
- Уравнения прямой на плоскости в координатной форме
- Уравнение прямой в пространстве
- Уравнения прямой в пространстве в координатной форме
- Параметрические уравнения прямой
- Параметрические уравнения прямой в канонической форме
- Уравнение прямой, проходящей через две точки
- Прямая как пересечение двух плоскостей
- Уравнения прямой в пространстве в векторной форме
- Векторное уравнение прямой в параметрической форме
- Векторные уравнения прямой
- Векторное уравнение прямой, проходящей через две точки
- Уравнения прямой в пространстве в координатной форме
Уравнение прямой на плоскости
Уравнения прямой на плоскости в координатной форме
Любую прямую линию на плоскости можно задать общим уравнением прямой в декартовой системе координат:
то есть числа одновременно не равны нулю.
Прямая линия на плоскости может быть задана параметрическим уравнением прямой:
где числа не равны нулю одновременно. Числа
являются компонентами направляющего вектора прямой — ненулевого вектора, лежащего на прямой.
Если
то после исключения из уравнений прямой в параметрической форме параметра
уравнение прямой приводятся к канонической форме:
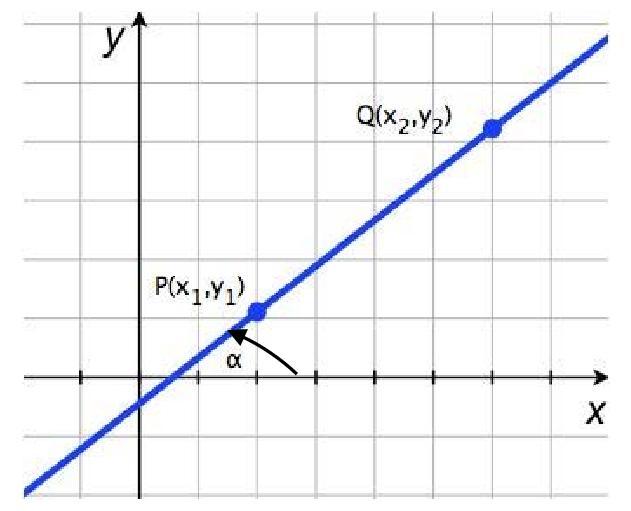
Уравнение прямой, проходящей через две точки и
:
При или
это уравнение принимает соответственно вид
или
Уравнения прямой на плоскости в векторной форме
Векторное уравнение прямой в параметрической форме:
где — направляющий вектор прямой,
— радиус-вектор некоторой точки прямой.
Нормальное векторное уравнение прямой:
где — вектор нормали к прямой.
Это уравнение также можно записать в форме
причём если вектор — единичный, то величина
есть расстояние от точки
до прямой. Вообще говоря, это уравнение имеет следующий смысл: проекция радиус-вектора любой точки прямой на нормаль к этой прямой постоянна.
Векторное уравнение прямой, проходящей через две различные точки:
где и
— радиус-векторы данных точек.
Это уравнение легко получается из векторного уравнения прямой в параметрической форме, если в качестве направляющего вектора прямой взять вектор
Уравнение прямой в пространстве
Уравнение прямой в пространстве в координатной форме
Прямая линия в пространстве может быть задана параметрическими уравнениями:
Числа являются компонентами направляющего вектора прямой.
Исключением параметра параметрические уравнения прямой приводятся к канонической форме:
Если, например, то канонические уравнения принимают вид
Аналогично для любой другой компоненты направляющего вектора.
Если два параметра равны нулю, например, то канонические уравнения имеют вид
Аналогично для любых других пар компонент направляющего вектора.
Уравнение прямой в пространстве, проходящей через две точки и
:
Если, например, то уравнения прямой принимают вид
Если к тому же то уравнения прямой записываются в виде
Аналогично для любых двух пар совпадающих координат точек.
Прямая в пространстве может быть задана как пересечение двух непараллельных плоскостей:
Уравнение прямой в пространстве в векторной форме
Прямая линия в пространстве может быть задана уравнением в параметрической форме:
где — направляющий вектор прямой,
— радиус-вектор некоторой точки прямой. Это уравнение совпадает с параметрическим векторным уравнением прямой на плоскости.
Прямую в пространстве можно задать векторными уравнениями:
или
Векторное уравнение прямой в пространстве, проходящей через две различные точки:
где и
— радиус-векторы двух точек прямой.
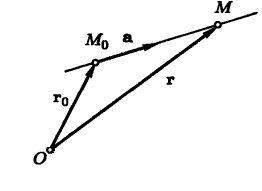
Векторное уравнение прямой в пространстве
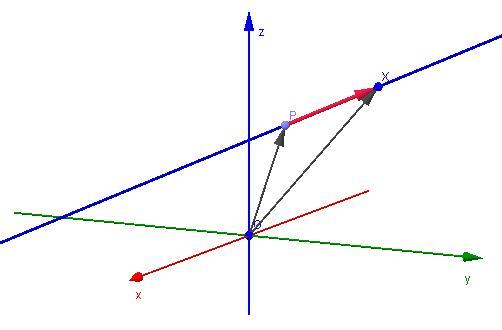
Пусть
для прямой известны
ее направляющий вектори
точка,
лежащая на этой прямой. Пусть—
произвольная (текущая) точка прямой.
Обозначим черезиr радиус-векторы
точек и
соответственно
(рис. 11.11).
Рис.11.11.Векторное
уравнение прямой
Тогда
вектор 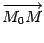
векторуp и,
следовательно, ,
где—
некоторое число. Из рис. 11.11 видно, что
|
|
(11.12) |
Это
уравнение называется векторным
уравнением прямой
или уравнением
в векторной форме.
При каждом значении параметра мы
будем получать новую точкуна
прямой.
Общие уравнения прямой в пространстве
Линия
в трехмерном пространстве определяется,
вообще говоря, пересечением двух
поверхностей, т.е. описывается системой
двух уравнений.
Прямую
в пространстве можно рассматривать как
линию пересечения двух плоскостей и,
следовательно, описывать системой двух
линейных уравнений
|
м |
|
|||||
при
условии, что эти плоскости непараллельны,
т.е. их нормальные векторы неколлинеарны.
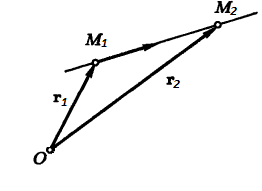
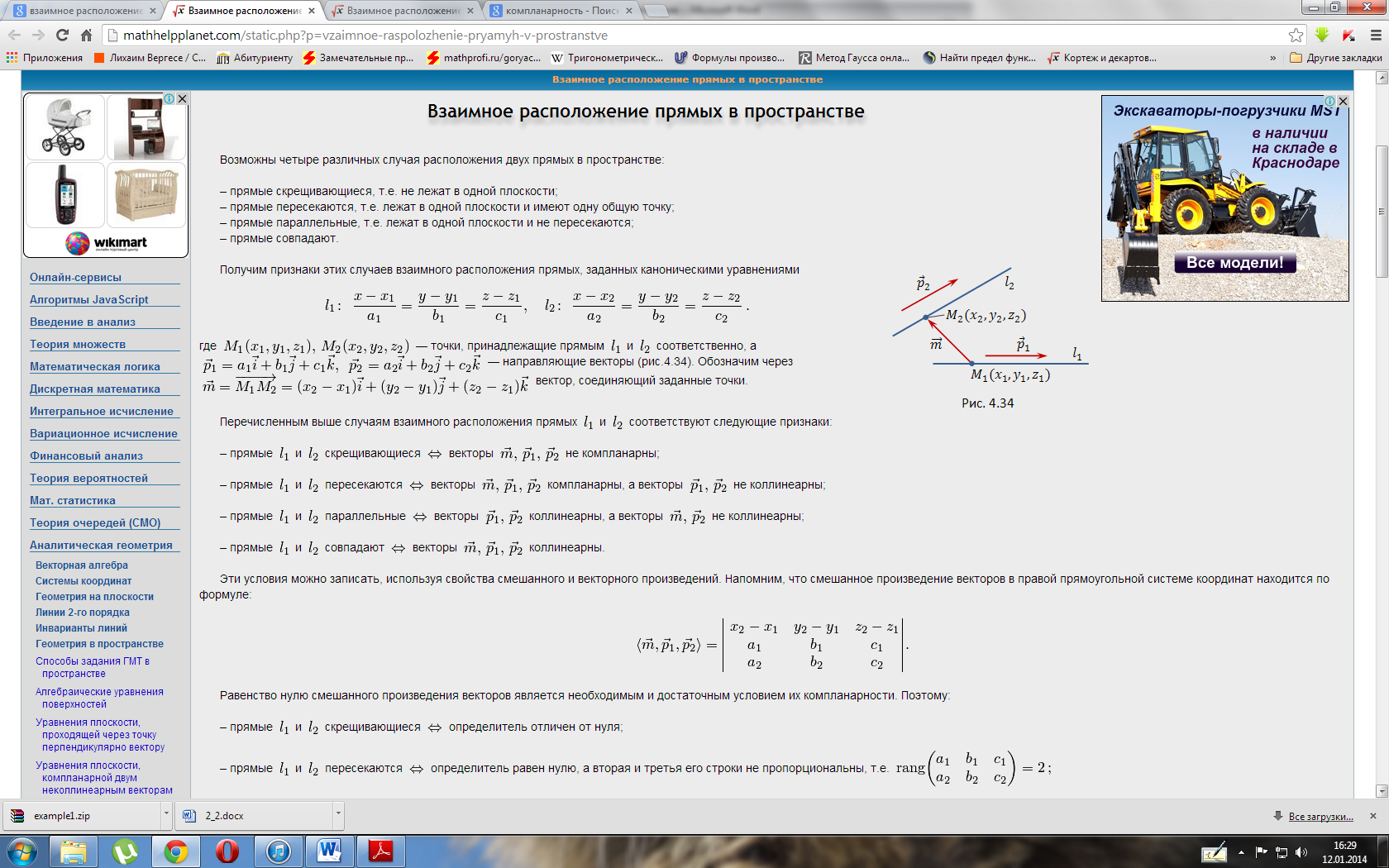
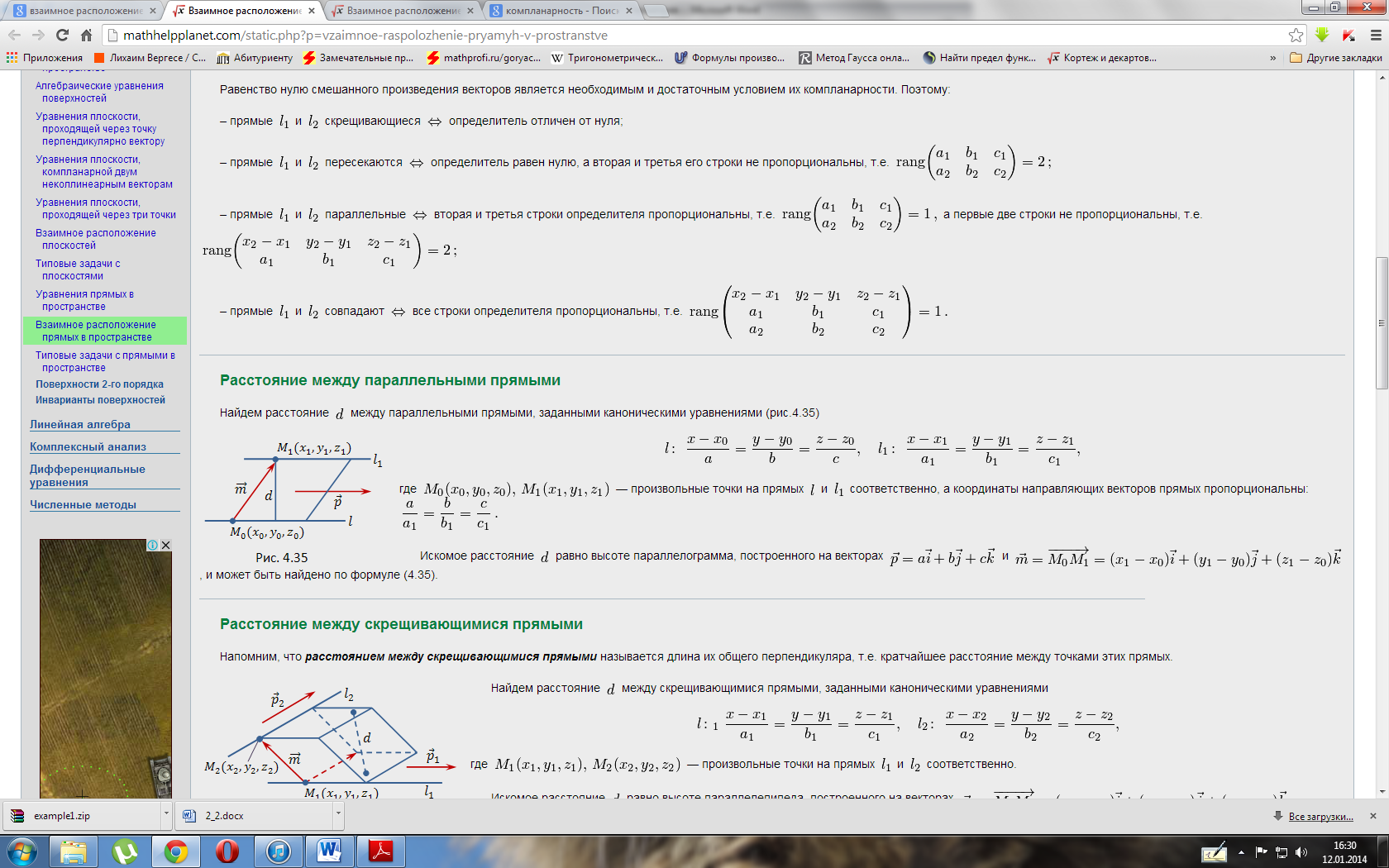
Расстояние
между скрещивающимися прямыми в
пространстве
-
В
трехмерном пространстве в прямоугольной
системе координат Oxyz заданы две
скрещивающиеся прямые a и b.
Прямую a определяют параметрические
уравнения прямой в пространствевида
X=-2
Y=2t+1
Z=-3t+4
,
а прямую b – канонические
уравнения прямой в пространстве.
Найдите расстояние между заданными
скрещивающимися прямыми.
Очевидно,
прямая a проходит через точку и
имеет направляющий вектор.
Прямая b проходит через точку,
а ее направляющим вектором является
вектор.
Вычислим
векторное произведение векторов и
:
Таким
образом, нормальный вектор 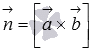
,
проходящей через прямую b параллельно
прямой a, имеет координаты.
Тогда
уравнение плоскости есть
уравнение плоскости, проходящей через
точкуи
имеющей нормальный вектор:
Нормирующий
множитель для общего уравнения
плоскости равен
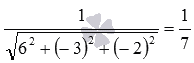
Следовательно, нормальное уравнение
этой плоскости имеет вид.
Осталось
воспользоваться формулой для вычисления
расстояния от точки до
плоскости:
Это
и есть искомое расстояние между заданными
скрещивающимися прямыми.
УГОЛ
МЕЖДУ ПРЯМЫМИ
Углом между
прямыми в пространстве будем называть
любой из смежных углов, образованных
двумя прямыми, проведёнными через
произвольную точку параллельно данным.
Пусть
в пространстве заданы две прямые:
Очевидно,
что за угол φ между прямыми можно принять
угол между их направляющими векторами и
.
Так как,
то по формуле для косинуса угла между
векторами получим
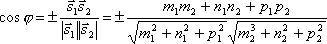
Условия
параллельности и перпендикулярности
двух прямых равносильны условиям
параллельности и перпендикулярности
их направляющих векторов и
:
Две
прямые параллельны тогда
и только тогда, когда их соответствующие
коэффициенты пропорциональны,
т.е. l1 параллельна l2 тогда
и только тогда, когда параллелен
.
Две
прямые перпендикулярны тогда
и только тогда, когда сумма произведений
соответствующих коэффициентов равна
нулю: .
Примеры.
-
Найти
угол между прямымии
.
-
Найти
уравнения прямой проходящей через
точку М1(1;2;3)
параллельно прямой l1:
Поскольку
искомая прямая l параллельна l1,
то в качестве направляющего вектора
искомой прямой l можно
взять направляющий вектор прямой l1.
-
Составить
уравнения прямой, проходящей через
точку М1(-4;0;2)
и перпендикулярной прямым:и
.
Направляющий
вектор прямой l можно
найти как векторное произведение
векторов и
:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
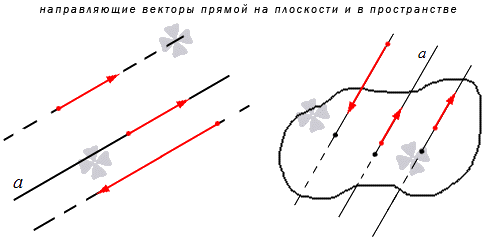
Направляющий вектор прямой, координаты направляющего вектора прямой
С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.
Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.
Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .
Как вычислить координаты направляющего вектора по уравнениям прямой
Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.
1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
Допустим, у нас есть канонический случай уравнения, которое имеет вид x – x 1 a x = y – y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
В прямоугольной системе координат задана прямая, которую можно описать уравнением x – 1 4 = y + 1 2 – 3 . Вычислите координаты одного из направляющих векторов прямой.
Решение
Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , – 3 . Это и будет нужный нам ответ.
Ответ: 4 , – 3 .
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = – 1 y = 7 – 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.
Решение
Для начала перепишем данные параметрические уравнения в виде x = – 1 + 0 · λ y = 7 – 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , – 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.
Ответ: 0 , – 5 · t , t ∈ R , t ≠ 0
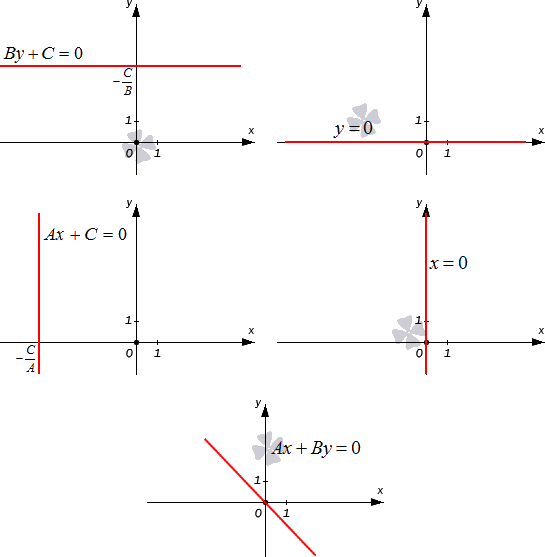
Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .
А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.
У нас есть прямая, заданная при помощи общего уравнения x – 2 = 0 . Найдите координаты любого направляющего вектора.
Решение
В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.
Ответ: ( 0 , 1 )
А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Есть прямая на плоскости, заданная уравнением 3 x + 2 y – 10 = 0 . Запишите координаты любого направляющего вектора.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:
3 x + 2 y – 10 = 0 ⇔ 3 x = – 2 y + 10
Получившееся равенство преобразовываем и получаем:
3 x = – 2 y + 10 ⇔ 3 x = – 2 ( y – 5 ) ⇔ x – 2 = y – 5 3
Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3
К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:
1) канонического уравнения прямой в пространстве x – x 1 a x = y – y 1 a y = z – z 1 a z
2) параметрического уравнения прямой в пространстве x – x 1 a x = y – y 1 a y = z – z 1 a z
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Прямая в пространстве задана уравнением вида x – 1 4 = y + 1 2 0 = z – 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.
Решение
В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , – 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , – 3 · t при условии, что t является действительным числом.
Ответ: 4 · t , 0 , – 3 · t , t ∈ R , t ≠ 0
Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = – 4 – λ .
Решение
Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = – 4 – 1 · λ .
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?
Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 – это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.
Решим задачу, в которой применяется этот подход.
Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z – 1 = 0 2 x + 4 y – 4 z + 5 = 0 .
Решение
Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z – 1 = 0 и 2 x + 4 y – 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , – 4 .
У нас получится:
n 1 → × n 2 → = i → j → k → 1 2 3 2 4 – 4 = i → · 2 · ( – 4 ) + j → · 3 · 2 + k → · 1 · 4 – – k → · 2 · 2 – i → · 3 · 4 – j → · 1 · ( – 4 ) = – 20 · i → + 10 · j → + 0 · k →
Выходит, что вектор n 1 → × n 2 → = – 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = – 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.
Ответ: – 20 , 10 , 0
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.
Уравнения прямых и плоскостей
Поверхности и линии первого порядка.
Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть (A^<2>+B^<2>+C^ <2>neq 0). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,label
$$
при условии (A^<2>+B^ <2>neq 0).
В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения eqref и eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.
В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.
В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.
Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.
Параметрические уравнения прямой и плоскости.
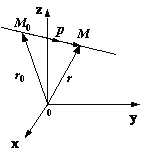
Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.
Рис. 6.1
Вектор (overrightarrowM> = boldsymbol-boldsymbol_<0>), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда (M) также лежит на прямой. В этом и только этом случае для точки (M) найдется такое число (t), что
$$
boldsymbol-boldsymbol_ <0>= tboldsymbol.label
$$
Наоборот, какое бы число мы ни подставили в формулу eqref в качестве (t), вектор (boldsymbol) в этой формуле определит некоторую точку на прямой.
Уравнение eqref называется векторным параметрическим уравнением прямой, а переменная величина (t), принимающая любые вещественные значения, называется параметром.
Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.
Получим теперь параметрические уравнения плоскости. Обозначим через (boldsymbol
) и (boldsymbol) ее направляющие векторы, а через (boldsymbol_<0>) — радиус-вектор ее начальной точки (M_<0>). Пусть точка (M) с радиус-вектором (boldsymbol) — произвольная точка пространства (рис. 6.2).
Рис. 6.2
Вектор (overrightarrowM> = boldsymbol-boldsymbol_<0>), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец (M) также лежит на плоскости. Так как (boldsymbol
) и (boldsymbol) не коллинеарны, в этом и только этом случае (boldsymbol-boldsymbol_<0>) может быть по ним разложен. Поэтому, если точка (M) лежит в плоскости (и только в этом случае), найдутся такие числа (t_<1>) и (t_<2>), что
$$
boldsymbol-boldsymbol_ <0>= t_<1>boldsymbol
+t_<2>boldsymbol.label
$$
Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров (t_<1>) и (t_<2>). Наоборот, какие бы числа мы ни подставили как значения (t_<1>) и (t_<2>), уравнение eqref определит некоторую точку плоскости.
Пусть ((x, y, z)) и ((x_<0>, y_<0>, z_<0>)) — координаты точек (M) и (M_<0>) соответственно, а векторы (boldsymbol
) и (boldsymbol) имеют компоненты ((p_<1>, p_<2>, p_<3>)) и ((q_<1>, q_<2>, q_<3>)). Тогда, раскладывая по базису обе части уравнения eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>, y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>, z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.label
$$
Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра (t), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.
Прямая линия на плоскости.
Поэтому мы можем сформулировать следующее утверждение.
В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой (M_<0>(x_<0>, y_<0>)) и направляющим вектором (boldsymbol(a_<1>, a_<2>)) может быть записано в виде eqref.
Уравнение eqref линейное. Действительно, после преобразования оно принимает вид (a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0), то есть (Ax+By+C = 0), где (A = a_<2>), (B = -a_<1>) и (C = a_<1>y_<0>-a_<2>x_<0>).
Вектор с координатами ((-B, A)) можно принять за направляющий вектор прямой с уравнением eqref в общей декартовой системе координат, а точку eqref за начальную точку.
Если система координат декартова прямоугольная, то вектор (boldsymbol(A, B)) перпендикулярен прямой с уравнением eqref.
Действительно, в этом случае ((boldsymbol, boldsymbol) = -BA+AB = 0).
Пусть в уравнении прямой (Ax+By+C = 0) коэффициент (B) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,label
$$
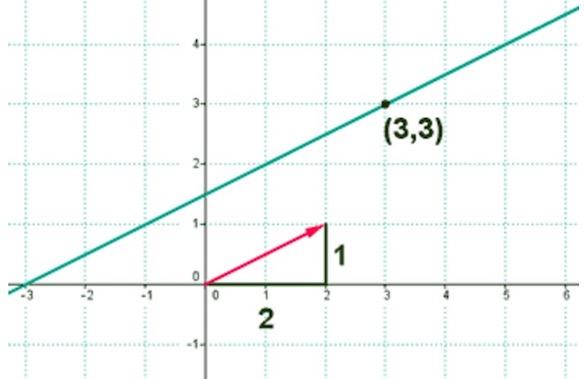
где (k = -A/B), а (b = -C/B). Мы видим, что к равно отношению компонент направляющего вектора: (k = a_<2>/a_<1>) (рис. 6.3).
Рис. 6.3. k=-1. Прямая y=-x+1/2
Отношение компонент направляющего вектора (a_<2>/a_<1>) называется угловым коэффициентом прямой.
Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от (boldsymbol_<1>) к (boldsymbol_<2>) (рис. 6.4).
Рис. 6.4. (k=operatornamevarphi = -1). Прямая (y=-x+1/2)
Положив (x = 0) в уравнении eqref, получаем (y = b). Это означает, что свободный член уравнения (b) является ординатой точки пересечения прямой с осью ординат.
Если же в уравнении прямой (B = 0) и ее уравнение нельзя представить в виде eqref, то обязательно (A neq 0). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид (x = x_<0>), где (x_ <0>= -C/A) — абсцисса точки пересечения прямой с осью абсцисс.
Векторные уравнения плоскости и прямой.
Параметрическое уравнение плоскости утверждает, что точка (M) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки (M_<0>) компланарна направляющим векторам (boldsymbol
) и (boldsymbol). Эту компланарность можно выразить и равенством
$$
(boldsymbol-boldsymbol_<0>, boldsymbol
, boldsymbol) = 0.label
$$
Вектор (boldsymbol = [boldsymbol
, boldsymbol]) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение eqref в виде
$$
(boldsymbol-boldsymbol_<0>, boldsymbol) = 0.label
$$
Уравнения eqref и eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в eqref (D = -(boldsymbol_<0>, boldsymbol)), получим
$$
(boldsymbol, boldsymbol)+D = 0.label
$$
Для прямой на плоскости можно также написать векторные уравнения, аналогичные eqref и eqref,
$$
(boldsymbol-boldsymbol_<0>, boldsymbol) = 0 mbox<или> (boldsymbol, boldsymbol)+C = 0.nonumber
$$
Первое из них выражает тот факт, что вектор (boldsymbol-boldsymbol_<0>) перпендикулярен ненулевому вектору (boldsymbol), перпендикулярному направляющему вектору (boldsymbol), и потому коллинеарен (boldsymbol).
Пусть (x, y, z) — компоненты вектора (boldsymbol) в общей декартовой системе координат. Тогда скалярное произведение ((boldsymbol-boldsymbol_<0>, boldsymbol)) при (boldsymbol neq 0) записывается линейным многочленом (Ax+By+Cz+D), где ((A^<2>+B^<2>+C^ <2>neq 0)).
Обратно, для любого линейного многочлена найдутся такие векторы (boldsymbol_<0>) и (boldsymbol neq 0), что в заданной общей декартовой системе координат (Ax+By+Cz+D = (boldsymbol-boldsymbol_<0>, boldsymbol)).
Первая часть предложения очевидна: подставим разложение вектора (boldsymbol) по базису в данное скалярное произведение:
$$
(xboldsymbol_<1>+yboldsymbol_<2>+zboldsymbol_<3>-boldsymbol_<0>, boldsymbol),nonumber
$$
раскроем скобки и получим многочлен (Ax+By+Cz+D), в котором (D = -(boldsymbol_<0>, boldsymbol)) и
$$
A = (boldsymbol_<1>, boldsymbol), B = (boldsymbol_<2>, boldsymbol), C = (boldsymbol_<3>, boldsymbol)label
$$
(A), (B) и (C) одновременно не равны нулю, так как ненулевой вектор (boldsymbol) не может быть ортогонален всем векторам базиса.
Для доказательства обратного утверждения найдем сначала вектор (boldsymbol) из равенств eqref, считая (A), (B) и (C) заданными. Из ранее доказанного утверждения 10 следует, что
$$
boldsymbol = frac_<2>, boldsymbol_<3>]><(boldsymbol_<1>, boldsymbol_<2>, boldsymbol_<3>)>+frac_<3>, boldsymbol_<1>]><(boldsymbol_<1>, boldsymbol_<2>, boldsymbol_<3>)>+frac_<1>, boldsymbol_<2>]><(boldsymbol_<1>, boldsymbol_<2>, boldsymbol_<3>)>.label
$$
Вектор (boldsymbol_<0>) должен удовлетворять условию (D = -(boldsymbol_<0>, boldsymbol)). Один из таких векторов можно найти в виде (boldsymbol_ <0>= lambda boldsymbol). Подставляя, видим, что (-lambda(boldsymbol, boldsymbol) = D), откуда (boldsymbol_ <0>= -Dboldsymbol/|boldsymbol|^<2>).
Итак, мы нашли векторы (boldsymbol) и (boldsymbol_<0>) такие, что линейный многочлен записывается в виде
$$
x(boldsymbol_<1>, boldsymbol)+y(boldsymbol_<2>, boldsymbol)+z(boldsymbol_<3>, boldsymbol)-(boldsymbol_<0>, boldsymbol),nonumber
$$
который совпадает с требуемым ((boldsymbol-boldsymbol_<0>, boldsymbol)).
Если система координат декартова прямоугольная, то вектор с компонентами (A), (B), (C) является нормальным вектором для плоскости с уравнением (Ax+By+Cz+D = 0).
Это сразу вытекает из формул eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.
Любые два неколлинеарных вектора, удовлетворяющие уравнению eqref, можно принять за направляющие векторы плоскости.
Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.
Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.
Действительно, (alpha_<1>, alpha_<2>), должны быть пропорциональны компонентам — (B), (A) направляющего вектора прямой.
Параллельность плоскостей и прямых на плоскости.
Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.
Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0, A_<1>x+B_<1>y+C_ <1>= 0,nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ <1>= lambda A, B_ <1>= lambda B.label
$$
Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения eqref выполнено (с тем же (lambda)) равенство
$$
C_ <1>= lambda C.label
$$
Первая часть предложения прямо следует из того, что векторы с компонентами ((-B, A)) и ((-B_<1>, A_<1>)) — направляющие векторы прямых.
Докажем вторую часть. В равенствах eqref и eqref (lambda neq 0), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.
Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид (Ax+By+C = 0) и (lambda(Ax+By)+C_ <1>= 0) при некотором (lambda). Если, кроме того, существует общая точка (M_<0>(x_<0>, y_<0>)) обеих прямых, то (Ax_<0>+By_<0>+C = 0) и (lambda(Ax_<0>+By_<0>)+C_ <1>= 0). Вычитая одно равенство из другого, получаем (C_ <1>= lambda C), как и требовалось.
Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0, A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ <1>= lambda A, B_ <1>= lambda B, C_ <1>= lambda C.label
$$
Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений eqref выполнено (с тем же (lambda)) равенство
$$
D_ <1>= lambda D.label
$$
Если плоскости параллельны, то их нормальные векторы (boldsymbol) и (boldsymbol_<1>) коллинеарны, и существует такое число (lambda), что (boldsymbol_ <1>= lambdaboldsymbol). В силу уравнений eqref (A_ <1>= (boldsymbol_<1>, boldsymbol_<1>) = lambda(boldsymbol_<1>, boldsymbol) = lambda A). Аналогично доказываются и остальные равенства eqref. Обратно, если равенства eqref выполнены, то из формулы eqref следует, что (boldsymbol_ <1>= lambdaboldsymbol). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.
Условия eqref выражают не что иное, как коллинеарность векторов с компонентами ((A, B)) и ((A_<1>, B_<1>)). Точно так же условия eqref означают коллинеарность векторов с компонентами ((A, B, C)) и ((A_<1>, B_<1>, C_<1>)). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
begin
A& B\
A_<1>& B_<1>
end
= 0,label
$$
а условие параллельности плоскостей — в виде
$$
begin
B& C\
B_<1>& C_<1>
end =
begin
C& A\
C_<1>& A_<1>
end =
begin
A& B\
A_<1>& B_<1>
end
= 0.label
$$
Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.
При условии eqref система линейных уравнений
$$
Ax+By+C = 0, A_<1>x+B_<1>y+C_ <1>= 0,nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от (C) и (C_<1>). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
begin
A& B\
A_<1>& B_<1>
end
neq 0.nonumber
$$
то при любых (C) и (C_<1>) система имеет единственное решение ((x, y)).
Уравнения прямой в пространстве.
Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
left<begin
Ax+By+Cz+D = 0,\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
endright.label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно eqref означает, что хоть один из детерминантов отличен от нуля:
$$
begin
B& C\
B_<1>& C_<1>
end^ <2>+
begin
C& A\
C_<1>& A_<1>
end^ <2>+
begin
A& B\
A_<1>& B_<1>
end^<2>
neq 0.label
$$
Разумеется, систему eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.
Вспомним параметрические уравнения прямой eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = frac><alpha_<1>>, t = frac><alpha_<2>>, t = frac><alpha_<3>>,nonumber
$$
и мы получаем два равенства
$$
frac><alpha_<2>> = frac><alpha_<3>>, frac><alpha_<1>> = frac><alpha_<3>>,label
$$
или, в более симметричном виде,
$$
frac><alpha_<1>> = frac><alpha_<2>> = frac><alpha_<3>>,label
$$
Уравнения eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная (x)), а вторая параллельна оси ординат.
Если обращается в нуль одна из компонент направляющего вектора, например, (alpha_<1>), то уравнения прямой принимают вид
$$
x = x_<0>, frac><alpha_<2>> = frac><alpha_<3>>,label
$$
Эта прямая лежит в плоскости (x = x_<0>) и, следовательно, параллельна плоскости (x = 0). Аналогично пишутся уравнения прямой, если в нуль обращается не (alpha_<1>), а другая компонента.
Когда равны нулю две компоненты направляющего вектора, например, (alpha_<1>) и (alpha_<2>), то прямая имеет уравнения
$$
x = x_<0>, y = y_<0>.label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.
Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений eqref. По условию eqref один из детерминантов отличен от нуля. Допустим для определенности, что (AB_<1>-A_<1>B neq 0). В силу утверждения 9 при любом фиксированном (z) система уравнений будет иметь единственное решение ((x, y)), в котором (x) и (y), разумеется, зависят от (z). Они — линейные многочлены от (z): (x = alpha_<1>z+beta_<1>), (y = alpha_<2>z+beta_<2>).
Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя (z) на (t), получаем параметрические уравнения прямой
$$
x = alpha_<1>t+beta_<1>, y = alpha_<2>t+beta_<2>, z = t.nonumber
$$
Первые две координаты начальной точки прямой (M_<0>(beta_<1>, beta_<2>, 0)) можно получить, решая систему eqref при значении (z = 0).
Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты ((alpha_<1>, alpha_<2>, 1)). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами ((A, B, C)) и (A_<1>, B_<1>, C_<1>) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
begin
B& C\
B_<1>& C_<1>
end,
begin
C& A\
C_<1>& A_<1>
end,
begin
A& B\
A_<1>& B_<1>
end.label
$$
Вектор с компонентами eqref есть направляющий вектор прямой с уравнениями eqref, какова бы ни была декартова система координат.
Согласно утверждению 5 каждый ненулевой вектор, компоненты которого ((alpha_<1>, alpha_<2>, alpha_<3>)) удовлетворяют уравнению (Aalpha_<1>+Balpha_<2>+Calpha_ <3>= 0), параллелен плоскости с уравнением (Ax+By+Cz+D = 0). Если, кроме того, он удовлетворяет уравнению (A_<1>alpha_<1>+B_<1>alpha_<2>+C_<1>alpha_ <3>= 0), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами eqref ненулевой в силу неравенства eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.
Направляющий вектор прямой: определение и примеры
Важным геометрическим объектом, который изучают в плоском пространстве, является прямая. В трехмерном же пространстве, помимо прямой, появляется еще плоскость. Оба объекта удобно задавать с помощью направляющих векторов. Что это такое, как применяют эти вектора для определения уравнений прямой и плоскости? Эти и другие вопросы освещаются в статье.
Прямая и способы ее задавания
Каждый школьник хорошо представляет, о каком геометрическом объекте идет речь. С точки зрения математики, прямая представляет собой набор точек, которые в случае их попарного произвольного соединения между собой приводят к получению совокупности параллельных векторов. Это определение прямой используют для написания уравнения для нее как в двумерном, так и в трехмерном пространстве.

Для описания рассматриваемого одномерного объекта пользуются разными видами уравнений, которые перечислены в списке ниже:
- общего вида;
- параметрическое;
- векторное;
- каноническое или симметричное;
- в отрезках.
Каждый из названных видов имеет некоторые преимущества по отношению к другим. Например, уравнением в отрезках удобно пользоваться при изучении поведения прямой относительно осей координат, уравнение общего вида удобно при нахождении направления, перпендикулярного заданной прямой, а также при вычислении угла ее пересечения с осью x (для плоского случая).

Поскольку тема данной статьи связана с направляющим вектором прямой, то далее будем рассматривать только уравнение, где этот вектор является принципиальным и содержится явно, то есть векторное выражение.
Задание прямой через вектор
Предположим, что у нас имеется некоторый вектор v¯ с известными координатами (a; b; c). Поскольку координат три, то вектор задан в пространстве. Как изобразить его в прямоугольной системе координат? Делается это очень просто: на каждой из трех осей откладывается отрезок, длина которого равна соответствующей координате вектора. Точка пересечения трех перпендикуляров, восстановленных к плоскостям xy, yz и xz, будет концом вектора. Началом же его является точка (0; 0; 0).
Тем не менее приведенное положение вектора не является единственным. Аналогичным образом можно нарисовать v¯, располагая его начало в произвольной точке пространства. Эти рассуждения говорят о том, что задать конкретную прямую с помощью вектора нельзя. Он задает семейство из бесконечного числа параллельных прямых.
Теперь зафиксируем некоторую точку P(x0; y0; z0) пространства. И зададим условие: через P должна проходить прямая. В этом случае вектор v¯ тоже должен содержать эту точку. Последний факт означает, что можно задать одну единственную прямую, используя P и v¯. Она запишется в виде следующего уравнения:
Здесь Q – любая точка, принадлежащая прямой. Эту точку можно получить, подобрав соответствующий параметр λ. Записанное уравнение называется векторным, а v¯ получил название направляющего вектора прямой. Располагая его так, чтобы он проходил через P, и изменяя его длину с помощью параметра λ, мы получаем каждую точку Q прямой.
В координатной форме уравнение запишется так:
(x; y; z) = (x0; y0; z0) + λ × (a; b; c)
И в явном (параметрическом) виде можно записать:
Если в приведенных выражениях исключить третью координату, то мы получим векторные уравнения прямой на плоскости.
Для каких задач полезно знать направляющий вектор ?
Как правило, это задачи на определение параллельности и перпендикулярности прямых. Также определяющий направление прямой вектор используется при вычислении дистанции между прямыми и точкой и прямой, для описания поведения прямой относительно плоскости.
Две прямые будут параллельными, если таковыми являются их направляющие вектора. Соответственно, перпендикулярность прямых доказывается с помощью перпендикулярности их векторов. В этих типах задач достаточно рассчитать скалярное произведение рассматриваемых векторов, чтобы получить ответ.
В случае задач на вычисление расстояний между прямыми и точками направляющий вектор входит явно в соответствующую формулу. Запишем ее:
Здесь P1P2¯ – построенный на точках P1 и P2 направленный отрезок. Точка P2 является произвольной, лежащей на прямой с вектором v¯, точка же P1 является той, до которой следует определить расстояние. Она может быть как самостоятельной, так и принадлежать другой прямой или плоскости.
Отметим, что рассчитывать расстояние между прямыми имеет смысл только тогда, когда они являются параллельными или скрещивающимися. Если же они пересекаются, то d равно нулю.
Приведенная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой, только в этом случае P1 должна принадлежать плоскости.
Решим несколько задач, чтобы нагляднее показать, как пользоваться рассматриваемым вектором.
Задача на составление векторного уравнения
Известно, что прямая описывается следующим равенством:
Следует написать соответствующее выражение в векторной форме.
Это типичное уравнение прямой, известное каждому школьнику, записано в общем виде. Покажем, как его переписать в векторной форме.
Выражение можно представить в виде:
Видно, что если его раскрыть, то получится исходное равенство. Теперь разделим его правую часть на два вектора так, чтобы только один из них содержал иксы, имеем:
(x; y) = (x; 3 × x) + (0; -4)
Остается вынести x за скобки, обозначить его греческим символом и поменять вектора правой части местами:
(x; y) = (0; -4) + λ × (1; 3)
Мы получили векторную форму записи исходного выражения. Координаты направляющего вектора прямой равны (1; 3).
Задача на определение взаимного расположения прямых
В пространстве заданы две прямые:
(x; y; z) = (1; 0; -2) + λ × (-1; 3; 1);
(x; y; z) = (3; 2; 2) + γ × (1; 2; 0)
Они являются параллельными, скрещивающимися или пересекающимися?
Ненулевые вектора (-1; 3; 1) и (1; 2; 0) будут направляющими для этих прямых. Выразим в параметрической форме эти уравнения и подставим координаты первого во второе. Получаем:
x = 3 + γ = 1 – λ => γ = -2 – λ;
y = 2 + 2 × γ = 3 × λ => γ = 3 / 2 × λ – 1;
z = 2 = -2 + λ => λ = 4
Подставляем найденный параметр λ в два уравнения выше, получаем:
γ = 3 / 2 × λ – 1 = 5
Параметр γ не может одновременно принимать два разных значения. Это означает, что прямые не имеют ни одной общей точки, то есть являются скрещивающимися. Параллельными они не являются, так как ненулевые векторы не параллельны друг другу (для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго).
Математическое описание плоскости
Для задания плоскости в пространстве приведем уравнение общего вида:
A × x + B × y + C × z + D = 0
Здесь латинские большие буквы представляют собой конкретные числа. Первые три из них определяют координаты нормального вектора плоскости. Если его обозначить n¯, тогда:
Этот вектор является перпендикулярным плоскости, поэтому его называют направляющим. Его знание, а также известные координаты какой-либо точки, принадлежащей плоскости, однозначно задают последнюю.
Если точка P(x1; y1; z1) плоскости принадлежит, тогда свободный член D рассчитывается следующим образом:
D = -1 × (A × x1 + B × y1 + C × z1)
Решим пару задач с использованием общего уравнения для плоскости.
Задача на нахождение нормального вектора плоскости
Плоскость задана в следующем виде:
(y – 3) / 2 + (x + 1) / 3 – z / 4 = 1
Как найти направляющий вектор для нее?
Из приведенной выше теории следует, что координаты нормального вектора n¯ являются коэффициентами, стоящими перед переменными. В связи с этим для нахождения n¯ следует записать уравнение в общем виде. Имеем:
1 / 3 × x + 1 / 2 × y – 1 / 4 × z – 13 / 6 = 0
Тогда нормальный вектор плоскости равен:
Задача на составление уравнения плоскости
Даны координаты трех точек:
Как будет выглядеть уравнение плоскости, содержащей все эти точки.
Через три точки, которые одной прямой не принадлежат, можно провести только одну плоскость. Чтобы найти ее уравнение, сначала вычислим направляющий вектор плоскости n¯. Для этого поступим следующим образом: найдем произвольные два вектора, принадлежащие плоскости, и вычислим их векторное произведение. Оно даст вектор, который этой плоскости будет перпендикулярен, то есть n¯. Имеем:
M1M2¯ = (1; -1; 5); M1M3¯ = (-1; -2; -2);
n¯ = [M1M2¯ × M1M3¯] = (12; -3; -3)
Возьмем точку M1 для составления выражения плоскости. Получаем:
D = -1 × (12 × 1 + (-3) × 0 + (-3) × 0) = -12;
12 × x – 3 × y – 3 × z – 12 = 0 =>
4 × x – y – z – 4 = 0
Мы получили выражение общего типа для плоскости в пространстве, определив сначала направляющий вектор для нее.
Свойство векторного произведения следует запомнить при решении задач с плоскостями, поскольку оно позволяет простым способом определять координаты нормального вектора.
[spoiler title=”источники:”]
http://univerlib.com/analytic_geometry/vector_algebra/lines_and_planes_equations/
http://1ku.ru/obrazovanie/41097-napravljajushhij-vektor-prjamoj-opredelenie-i-primery/
[/spoiler]
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой (общее уравнение прямой на плоскости и его исследование). Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и его исследование, как осуществлять переходы от общего уравнения к другим типам уравнений прямой (неполного уравнения, полного уравнения). Всю теорию закрепим иллюстрациями и решением практических задач на уравнения.
Общее уравнение прямой: основные сведения
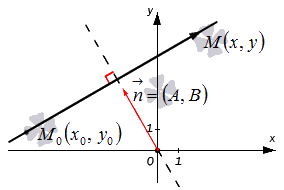
Как найти уравнение прямой? Пусть на плоскости задана прямоугольная система координат Oxy.
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B). Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.
Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.
Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).
Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n→, M0M→=A(x-x0)+B(y-y0)=0
Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение Ax+By+C=0.
Так, без какой-либо помощи онлайн мы смогли доказать и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy (уравнение прямой параллельной оси ox).
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.
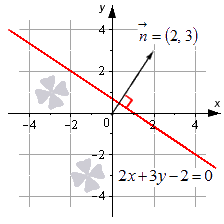
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию из уравнения с вектором на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
- Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
- Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
- Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
- Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11. Необходимо написать общее уравнение заданной прямой. Попробуем его составить.
Решение
Решение лежит на поверхности. Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т.е. верно равенство:
A·27+C=0
Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0
Ответ: 7x-2=0
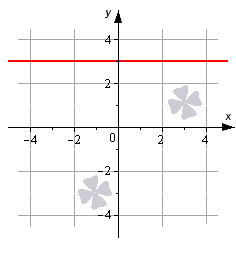
На чертеже изображена прямая, необходимо записать ее уравнение. Как будем это находить?
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).
Прямую, которая будет являться параллельной оси абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C. Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля. Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.
Ответ: y-3=0.
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0. Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой n→=(1, -2). Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:
A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0
Задачу можно решать иначе. Как она будет решаться? Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор (векторная прямая) позволяет получить значения коэффициентов A и B в уравнении прямой, тогда:
Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0
Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 – 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x – 2·y + 11=0.
Ответ: x – 2·y + 11=0.
Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
23×0-y0-12=0
Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52
Ответ: -52
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению x-x1ax=y-y1ay.
Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.
Это равенство возможно записать как пропорцию: x+CA-B=yA .
В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.
Перепишем равенство в виде пропорции: x-B=y+CBA .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.
Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.
Ответ: x-3=y-430.
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Перед нами задание. Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152
Теперь примем обе части полученного канонического уравнения равными λ, тогда:
x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R
Ответ: x=5·λy=-15+2·λ, λ∈R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.
Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2x+7y=0⇔7y-2x⇔y=-27x
Ответ: y=-27x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.
Решение
Перенесем 12 в правую часть: x-7y+12=0⇔x-7y=-12.
Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.
Ответ: x-12+y114=1.
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0
Каноническое уравнение преобразуется к общему по следующей схеме:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0
Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40
Перейдем от канонического к общему:
x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0
Ответ: y-4=0
Задано уравнение прямой в отрезках x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x3+y12=1⇔13x+2y-1=0
Ответ: 13x+2y-1=0.
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0
Ответ: 2x-3y-5=0.
Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.
Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:
A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0
Ответ: 3x+5y=0.
Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий[1], их свойства и связь с другими понятиями (например, точки и плоскости) определяются аксиомами геометрии[2].
Прямая, наряду с окружностью, относится к числу древнейших геометрических фигур. Античные геометры считали эти две кривые «совершенными» и поэтому признавали только построения с помощью циркуля и линейки. Евклид описал линию как «длину без ширины», которая «равно лежит на всех своих точках»[3].
Аналоги прямых могут быть определены также в некоторых типах неевклидовых пространств. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то отрезок прямой можно определить как самую короткую кривую, соединяющую эти точки. Например, в римановой геометрии роль прямых играют геодезические линии, которые являются кратчайшими; на сфере кратчайшими являются дуги больших кругов[4].
Свойства прямой в евклидовой геометрии[править | править код]
Участки прямой, ограниченные двумя её точками, называются отрезками.
- Через любую точку можно провести бесконечно много прямых.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке[5], или являются параллельными (следует из предыдущего).
- В трёхмерном пространстве существуют три варианта взаимного расположения двух несовпадающих прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
- Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости[править | править код]
Способы задания прямой:
Общее уравнение прямой[править | править код]
Общее уравнение прямой линии на плоскости в декартовых координатах:
где 



При 



Вектор с координатами 
При 
Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом[править | править код]
Уравнение прямой линии, пересекающей ось 



Коэффициент 
В этом виде невозможно представить прямую, параллельную оси 
Получение уравнения прямой в отрезках
Уравнение прямой в отрезках[править | править код]
Уравнение прямой линии, пересекающей ось 



В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой[править | править код]
где 




Если прямая задана общим уравнением 









Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие 



Уравнение прямой, проходящей через две заданные несовпадающие точки[править | править код]
Если заданы две несовпадающие точки с координатами 

или
или в общем виде
Получение векторного параметрического уравнения прямой
Векторное параметрическое уравнение прямой[править | править код]
Векторное параметрическое уравнение прямой задается вектором 


Параметрические уравнения прямой[править | править код]
Параметрические уравнения прямой могут быть записаны в виде:
где 



Смысл параметра 
Каноническое уравнение прямой[править | править код]
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где 




Уравнение прямой в полярных координатах[править | править код]
Уравнение прямой в полярных координатах 

или
Тангенциальное уравнение прямой[править | править код]
Тангенциальное уравнение прямой на плоскости:
Числа 

Уравнения прямой в пространстве[править | править код]
Векторное параметрическое уравнение прямой в пространстве:
где 



Параметрические уравнения прямой в пространстве:
где 
некоторой фиксированной точки 

Каноническое уравнение прямой в пространстве:
где 
некоторой фиксированной точки 

Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных плоскостей, заданных соответственно общими уравнениями:
и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[6]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой
на фиксированный направляющий вектор прямой
:
где фиксированный вектор 

Взаимное расположение точек и прямых на плоскости[править | править код]
Три точки 


Отклонение точки 

где знак перед радикалом противоположен знаку 
В пространстве расстояние от точки 
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент 
Взаимное расположение нескольких прямых на плоскости[править | править код]
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол 
При этом под 





Эти прямые параллельны, если 



Любую прямую, параллельную прямой с уравнением 

Если же уравнение прямой задано как 

Если знак перед радикалом противоположен 

Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если 



Некоторые специальные типы прямых[править | править код]
- Прямая Александрова
- Прямая Симсона
- Прямая Суслина[en]
- Прямая Эйлера
- Числовая прямая
Примечания[править | править код]
- ↑ Coxeter, 1969, p. 4
- ↑ Математическая энциклопедия, 1984, с. 721—722.
- ↑ Прокл Диадох. Комментарий к первой книге «Начал» Евклида / Университет Дмитрия Пожарского. — М., 2013. — С. 116. — 368 с.
- ↑ Норден А. П. Краткий курс дифференциальной геометрии. — М.: Физматгиз, 1958. — С. 214—215. — 244 с.
- ↑ Faber, Appendix B, p. 300.
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
Литература[править | править код]
- Маркушевич А. И. Замечательные кривые, Популярные лекции по математике. — Выпуск 4. — Гостехиздат, 1952 г. — 32 стр.
- Прямая // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
- Coxeter, H.S.M (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 0-471-18283-4
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, ISBN 0-8247-1748-1
- Pedoe, Dan (1988), Geometry: A Comprehensive Course, Mineola, NY: Dover, ISBN 0-486-65812-0
- Wylie, Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill, ISBN 0-07-072191-2
Ссылки[править | править код]
- Прямая на плоскости, справочник математических формул «Прикладная математика»
- Прямая в пространстве, справочник математических формул «Прикладная математика»


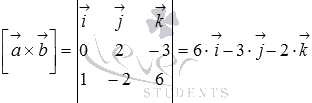
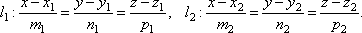
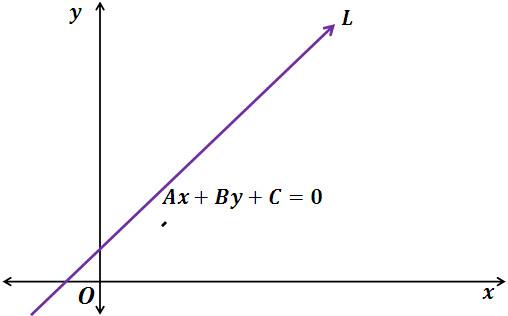


























![[{vec r},{vec a}]={vec M},](https://wikimedia.org/api/rest_v1/media/math/render/svg/940ec5302c287b63f2e45bbfb8501d3ec4133d15)












