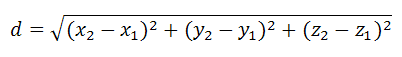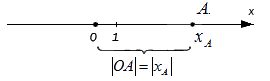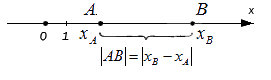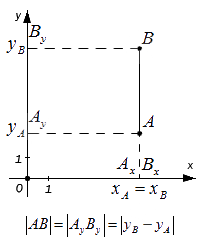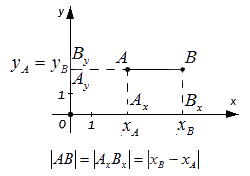Skip to content
Длина вектора в пространстве
Длиной (или модулем) вектора называется расстояние между началом и концом вектора.
Длина вектора a{X,Y,Z} выражается через его координаты следующей формулой:
Пример
Длина вектора $aleft{ { — 2,3,sqrt 3 } right}$ равна
$left| a right| = sqrt {{X^2} + {Y^2} + {Z^2}} = $
$sqrt {{{left( { — 2} right)}^2} + {3^2} + {{left( {sqrt 3 } right)}^2}} = sqrt {16} = 4$
Расстояние между двумя точками в пространстве
Расстояние d между точками в пространстве A1{x1;y1;z1}, A2{x2;y2;z2} представляется формулой
Пример
Расстояние между точками A1{4;-6;3} и A2 {-1;5;-4}
$d = sqrt {{{left( {{x_2} — {x_1}} right)}^2} + {{left( {{y_2} — {y_1}} right)}^2} + {{left( {{z_2} — {z_1}} right)}^2}} = $
$=sqrt {{{left( { — 1 — 4} right)}^2} + {{left( {5 — left( { — 6} right)} right)}^2} + {{left( { — 4 — 3} right)}^2}} =$
$ =sqrt {25 + 121 + 49} = sqrt {195} approx 14$
12647
Расстояние d между точками в пространстве A11;y1;z1>, A22;y2;z2> представляется формулой
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
3 комментария
найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн
Расстояние от точки до точки: формулы, примеры, решения
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
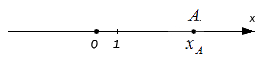
Исходные данные: координатная прямая O x и лежащая на ней произвольная точка А . Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число х A , оно же – координата точки А .
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О , необходимо будет отложить три единичных отрезка. Если точка А имеет координату – 4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние О А равно 3 ; во втором случае О А = 4 .
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4 111 .
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то O A = x A (число принимается за расстояние); если координата меньше нуля, то O A = – x A . В общем, эти утверждения справедливы для любого действительного числа x A .
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- x A , если x A > 0 ;
- – x A , если x A 0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты x A и x B : A B = x B – x A .
Расстояние между точками на плоскости
Исходные данные: точки A и B , лежащие на плоскости в прямоугольной системе координат O x y с заданными координатами: A ( x A , y A ) и B ( x B , y B ) .
Проведем через точки А и B перпендикуляры к осям координат O x и O y и получим в результате точки проекции: A x , A y , B x , B y . Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси O x (оси абсцисс), то точки и совпадают, а | А В | = | А y B y | . Поскольку, расстояние между точками равно модулю разности их координат, то A y B y = y B – y A , а, следовательно A B = A y B y = y B – y A .
– если точки A и B лежат на прямой, перпендикулярной оси O y (оси ординат) – по аналогии с предыдущим пунктом: A B = A x B x = x B – x A
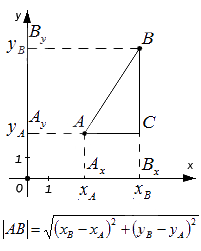
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Мы видим, что треугольник А В С является прямоугольным по построению. При этом A C = A x B x и B C = A y B y . Используя теорему Пифагора, составим равенство: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а затем преобразуем его: A B = A x B x 2 + A y B y 2 = x B – x A 2 + y B – y A 2 = ( x B – x A ) 2 + ( y B – y A ) 2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
A B = ( x B – x A ) 2 + ( y B – y A ) 2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: A B = ( x B – x A ) 2 + ( y B – y A ) 2 = 0 2 + 0 2 = 0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
A B = ( x B – x A ) 2 + ( y B – y A ) 2 = 0 2 + ( y B – y A ) 2 = y B – y A
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
A B = ( x B – x A ) 2 + ( y B – y A ) 2 = ( x B – x A ) 2 + 0 2 = x B – x A
Расстояние между точками в пространстве
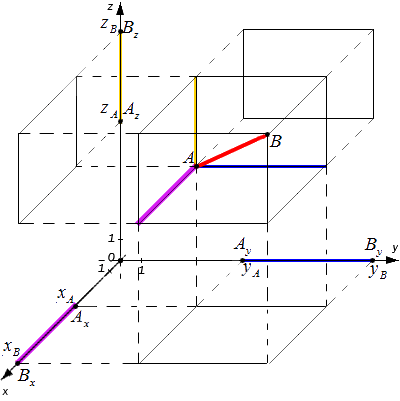
Исходные данные: прямоугольная система координат O x y z с лежащими на ней произвольными точками с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: A x , A y , A z , B x , B y , B z
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: A x B x , A y B y и A z B z
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
A x B x = x B – x A , A y B y = y B – y A , A z B z = z B – z A
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B – x A 2 + y B – y A 2 + z B – z A 2 = = ( x B – x A ) 2 + ( y B – y A ) 2 + z B – z A 2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
A B = x B – x A 2 + y B – y A 2 + ( z B – z A ) 2
Полученная формула действительна также для случаев, когда:
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A ( 1 – 2 ) и B ( 11 + 2 ) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 – 2 = 2 – 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 – ( 1 – 2 ) = 10 + 2 2
Ответ: O A = 2 – 1 , A B = 10 + 2 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A ( 1 , – 1 ) и B ( λ + 1 , 3 ) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .
Решение
Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = ( x B – x A ) 2 + y B – y A 2
Подставив реальные значения координат, получим: A B = ( λ + 1 – 1 ) 2 + ( 3 – ( – 1 ) ) 2 = λ 2 + 16
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Ответ: А В = 5 , если λ = ± 3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A ( 1 , 2 , 3 ) и B – 7 , – 2 , 4 .
Решение
Для решения задачи используем формулу A B = x B – x A 2 + y B – y A 2 + ( z B – z A ) 2
Подставив реальные значения, получим: A B = ( – 7 – 1 ) 2 + ( – 2 – 2 ) 2 + ( 4 – 3 ) 2 = 81 = 9
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/rasstojanie-mezhdu-tochkami/
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
[/spoiler]
Если
нам известны координаты точек (естественно,
в заданной системе координат), то
однозначно известно их положение.
Поэтому можно найти любые геометрические
характеристики их взаимного расположения.
Получим формулы, позволяющие по известным
координатам двух точек вычислить
расстояние между ними.
В
простейшем случае, когда две
точки А1 и А2 находятся
на одной оси, расстояние между ними
определяется формулой
s
= |x2 −
x1|,
(3)
где х1, х2 −
координаты точек А1 и А2 соответственно.
Очевидно,
что расстояние от А1 до А2 равно
расстоянию от А2 до А1,
что и привело у к тому, что в формуле (3)
появился знак модуля числа.
Пусть
на плоскости задана система координат ХОY,
в которой координаты точки А1 равны х1 и у1,
а координаты точки А2,
соответственно, равны х2 и у2 (рис.
8).

рис.
8
В
прямоугольном треугольнике А1А2В длина
стороны А2В равна |х2 −
х1|,
а длина стороны А1В
= |у2 −
у1|,
поэтому расстояние между точками А1 и А2 можно
найти по теореме Пифагора:
s
= √{(x2 −
x1)2 +
(y2 −
y1)2}.
(4)
26. Линейные операции над векторами. Линейные операции над векторами
Сложение
векторов
Пусть
даны два вектора
и
.
Приложим вектор
к
точке
(концу
вектора
)
и получим вектор
(рис.1.7,а;
здесь и далее равные векторы отмечены
одинаковыми засечками).
Вектор
называется суммой
векторов
и
и
обозначается
.
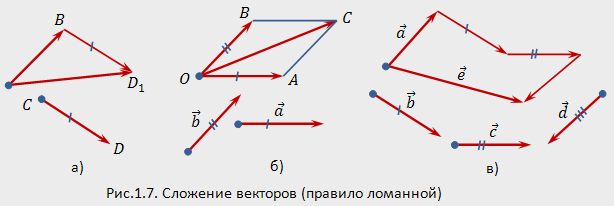
Это нахождение суммы называется правилом
треугольника.
Сумму
двух неколлинеарных векторов
и
можно
найти по правилу
параллелограмма.
Для этого откладываем от любой
точки
векторы
и
,
а затем строим параллелограмм
(рис.
1.7,6). Диагональ
параллелограмма
определяет сумму:
.
Для
нахождения суммы нескольких векторов
можно построить ломаную из равных им
векторов. Тогда замыкающий
вектор,
соединяющий начало первого вектора
ломаной с концом последнего ее вектора,
равен сумме всех векторов ломаной. На
рис.1.7,в изображена сумма
четырех
векторов
.
Таким способом (правило
ломаной)
можно сложить любое конечное число
векторов. Заметим, что сумма векторов
не зависит от точек приложения слагаемых
и от порядка суммирования. Например,
“выстраивая цепочку” векторов для
суммы в виде
,
получим вектор, равный вектору
.
Если ломаная получилась замкнутой, то
сумма равна нулевому вектору.

Вычитание
векторов
Вектор
называется противоположным вектору
,
если их сумма равна нулевому вектору:
.
Противоположный вектор
имеет
длину
,
коллинеарен и противоположно направлен
вектору
(рис.1.8,а,б).
Нулевой вектор является противоположным
самому себе.

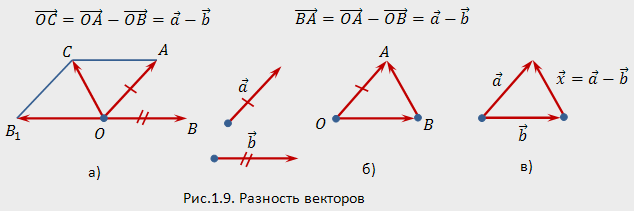
Разностью
векторов
и
называется
сумма вектора
с
вектором
,
противоположным вектору
:
Для
нахождения разности векторов
и
приложим
к произвольной точке
векторы
,
а также вектор
,
противоположный вектору
(рис.1.9,а).
Искомую разность находим по правилу
параллелограмма:
Для
нахождения разности проще использовать
правило треугольника (рис. 1.9,6). Для этого
прикладываем к произвольной
точке
векторы
.
Вектор
при
этом равен искомой разности
.
Вычитание
векторов — действие, обратное сложению
— можно определить также следующим
образом: разностью
векторов
и
называется
такой вектор
,
который в сумме с вектором
дает
вектор
(рис.1.9,в),
т.е. разность
—
это решение уравнения
.
Пример
1.2. Для
векторов на рис. 1.6 найти следующие суммы
и разности:
Решение. Учитывая
равенство
,
получаем по правилу треугольника
.
Поскольку
и
,
то
.
По
правилу параллелограмма
.
Так
как
и
,
находим
Умножение
вектора на число
Произведением
ненулевого вектора а на действительное
число
называется
вектор
,
удовлетворяющий условиям:
1)
длина вектора
равна
,
т.е.
;
2)
векторы
и
коллинеарные
;
3)
векторы
и
одинаково
направлены, если
,
и противоположно направлены, если
.
Произведение
нулевого вектора на любое число
считается
(по определению) нулевым вектором:
;
произведение любого вектора на число
нуль также считается нулевым вектором:
.
Из определения произведения следует,
что:
а)
при умножении на единицу
вектор
не изменяется:
;
б)
при умножении вектора на
получается
противоположный вектор:
;
в) деление
вектора на отличное от нуля число
сводится
к его умножению на число
,
обратное
.
г)
при делении ненулевого вектора
на
его длину, т.е. при умножении
на
число
получаем
единичный вектор, одинаково направленный
с вектором
.
Действительно,
длина вектора
равна
единице:
.
Вектор
коллинеарен
и одинаково направлен с вектором
,
так как
;
д)
при умножении единичного вектора на
число
получаем
коллинеарный ему вектор, длина которого
равна
.
На
рис.1.10 изображены векторы, получающиеся
в результате умножения данного
вектора
на
и
,
а также противоположный вектор
.

Свойства
линейных операций над векторами
Сложение
векторов и умножение вектора на число
называются линейными
операциями над векторами.
Для
любых векторов
и
любых действительных чисел
справедливы
равенства:
Свойства
1, 2 выражают коммутативность и
ассоциативность операции сложения
векторов, свойство 5 — ассоциативность
операции умножения на число, свойства
6,7 — законы дистрибутивности, свойство
8 называется унитарностью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ТЕМА 7.3 ДЛИНА
ВЕКТОРА, РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Содержание учебного материала:
Изучение
свойств векторных величин и скалярного произведения векторов:
1.Длина
радиус-вектора.
2.Расстояние
между двумя точками.
3.
Координаты точки середины отрезка.
4.
Координаты точки, делящей отрезок в заданном отношении.
5.Скалярное
произведение двух векторов и его свойства.
6.Координатная
форма скалярного произведения.
7.Условие
коллинеарности векторов в пространстве.
8.Условие
ортогональности векторов в пространстве.
1. Длина вектора {х; у; z} вычисляется по формуле:
|| =
.
2. Расстояние между точками А (х1; у1;
z1)
и В(х2; у2; z2) вычисляется по формуле:
|АВ| =
3. Координаты середины С(х; у; z) отрезка АВ, где А (х1;
у1; z1) и В(х2; у2; z2) вычисляются по формулам:
х = ; у =
; z =
.
4. Координаты точки С(х; у; z), делящей отрезок АВ в заданном отношении , где
– коэффициент пропорциональности, А (х1; у1;
z1),
В(х2; у2; z2), вычисляются по формулам:
х = ; у =
; z =
.

Определение. Скалярным произведением векторов
= (х1; у1;
z1) и (х2; у2; z2)
(рис.1) называется число, равное произведению их длин на косинус угла между
ними:
∙
= |
|∙|
|∙
.
6. Скалярное произведение векторов в координатной
форме равно:
∙
= х1х2 + у1у2
+ z1z2,
Из определения
скалярного произведения векторов находим угол
между векторами:
=
;
=
.
Свойства скалярного произведения для векторов ,
и
и любого числа k:
·
=
(переместительный
закон);
·
+
=
+
(распределительный
закон).
·
= (
)
(сочетательный закон).
7.Условие коллинеарности векторов в
пространстве.
Два вектора а = (х1;
у1; z1), b = (х2; у2;
z2)
являются коллинеарными, если
пропорциональны их соответствующие координаты:
8.Условие ортогональности векторов в
пространстве.
Два вектора а = (х1;
у1; z1), b = (х2; у2;
z2)
являются ортогональными, если их
скалярное произведение равно нулю:
Простейшие задачи в координатах
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
К простейшим задачам в координатах относятся следующие задачи:
-
Вычисление координат вектора по координатам его начала и конца.
-
Нахождение координат середины отрезка.
-
Вычисление длины вектора.
-
Вычисление расстояние между двумя точками.
Рассмотрим далее решение этих задач.
Вычисление координат вектора по координатам его начала и конца
Перед тем, как ввести данную задачу напомним понятие радиус вектора данной точки.
Определение 1
Пусть точка $M$ дана в заданной системе координат с началом в точке $O$. Тогда вектор $overrightarrow{OM}$ называется радиус-вектором для точки $M$.
Напомним, что при этом, если $M={x,y}$ в данной системе координат, то вектор $overrightarrow{OM}={x,y}$ в этой системе координат.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Пример 1
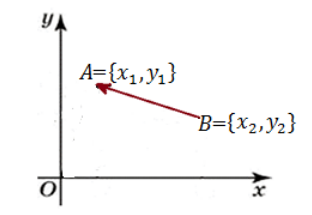
Даны точки $A$ и $B$ имеющие координаты $left{x_1, y_1right}$ и ${x_2, y_2}$ соответственно. Найти координаты вектора $overrightarrow{AB}.$
Решение.
Рассмотрим рисунок по данной задаче (Рис. 1).
Рисунок 1. Связь между координатами вектора и координатами его начала и конца
По определению разности двух векторов, имеем
[overrightarrow{AB}=overrightarrow{OB}-overrightarrow{OA}]
Следовательно,
[overrightarrow{AB}=left{x_2, y_2right}-left{x_1, y_1right}={x_2-x_1, y_2-y_1}]
Ответ: $overrightarrow{AB}={x_2-x_1, y_2-y_1}$.
Координаты середины отрезка
Пример 2
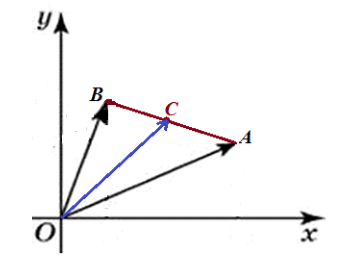
Даны точки $A$ и $B$ имеющие координаты $left{x_1, y_1right}$ и ${x_2, y_2}$ соответственно. $C$ — середина отрезка $AB$. Найти координаты точки $C.$
Решение.
Обозначим координаты точки $C$ через $left{x, yright}$. Рассмотрим рисунок 2.
Рисунок 2. Середина отрезка
Из правила параллелограмма, получим
[overrightarrow{OC}=frac{1}{2}(overrightarrow{OA}+overrightarrow{OB})]
Так как векторы $overrightarrow{OC}, overrightarrow{OA} и overrightarrow{OB}$ – радиус-векторы точек $C, A и B$ соответственно, то получим
[overrightarrow{OC}=left{x, yright}, overrightarrow{OA}=left{x_1, y_1right}, overrightarrow{OB}={x_2, y_2}]
Следовательно,
[x=frac{x_1+x_2}{2}, y=frac{y_1+y_2}{2}]
Ответ: $C=left{frac{x_1+x_2}{2}, frac{y_1+y_2}{2}right}$
«Простейшие задачи в координатах» 👇
Вычисление длины вектора по его координатам
Пример 3
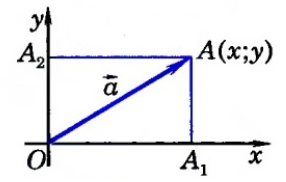
Дан вектор $overrightarrow{a}$ с координатами $left{x, yright}$. Найти длину этого вектора.
Решение.
Рассмотрим систему координат $xOy$. Отложим от ее начала координат вектор $overrightarrow{OA}=overrightarrow{a}$. Проведем через точку $A$ перпендикуляры к осям координат $OA_1$ и $OA_2$ (рис. 3).
Рисунок 3. Вычисление длины вектора
Так как вектор $overrightarrow{OA}$ – радиус вектор точки $A$, то $A=left{x, yright}$, следовательно,
[OA_1=x, OA_2=y]
Найдем теперь длины вектора по теореме Пифагора:
[{|overrightarrow{a}|}^2={OA_1}^2+{OA_2}^2] [{|overrightarrow{a}|}^2=x^2+y^2] [left|overrightarrow{a}right|=sqrt{x^2+y^2}]
Ответ: $sqrt{x^2+y^2}$.
Расстояние между двумя точками
Пример 4
Даны точки $A$ и $B$ имеющие координаты $left{x_1, y_1right}$ и ${x_2, y_2}$ соответственно.Найти $d$ — расстояние между точками $A$ и $B$ через их координаты.
Решение.
Рассмотрим рисунок 4.
Рисунок 4. Расстояние между точками
[ d=|overrightarrow{AB}|]
Используя задачу 1, получим, что вектор $overrightarrow{AB}$ имеет координаты
[overrightarrow{AB}={x_2-x_1, y_2-y_1}]
Найдем длину данного вектора. По задаче 3, имеем
[d=left|overrightarrow{AB}right|=sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}]
Ответ: $d=sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 05.04.2023