Вероятность как найти

Вероятность – это фундаментальная концепция, лежащая в основе многих областей нашей жизни, от игр в казино до ожидания зарплаты или создания плана мероприятий.

Узнать вероятность событий возможно благодаря законам теории вероятностей, дающим представление о том, как случайные события разворачиваются во времени. Необходимо осознать, что вероятность – численное значение, ограниченное в интервале от 0 до 1, обладающее свойствами, что предлагают способы определения ее пропорциональным выражением элементов общего множества событий.

Важно отметить, что одно из обобщенных способов определения теоретической вероятности – это применение математической формулы, позволяющей вычислять значение выражения на основе полномочий упарываний или теоретических предпосылок двух независимых событий. Другой распространенный аспект подхода к измерению вероятностей – эмпирический подход, представляющий собой способ поиска статистических закономерностей в данных экспериментальных облучестях.

Чтобы освоить способы нахождения вероятности, индивиду необходимо понимать математические основы понятий теории вероятностей и статистические принципы. В данной статье мы будем продумывать основные концепции вероятности, как темы теориеклогосу и практических примеров строительных таблиц конечных результатов.

Вероятность: основы теории и практическая сторона

Основы теории вероятностей

Теория вероятностей берёт начало в эпоху возникновения теории игры и зарождения ранней математики. Основными её концепциями являются:

Случайное событие – любое событие, результат которого зависит от случайности;
Пространство элементарных исходов – множество возможных результатов, или элементарных исходов;
Вероятностное пространство – математическая структура, состоящая из пространства элементарных исходов, σ-алгебры подмножеств и вероятностной меры, которая ставит каждому элементарному исходу в соответствие вероятность его наступления.

Помимо этого, в теории вероятностей существуют некоторые важные аксиомы для определения вероятности событий:

Вероятность каждого элементарного исхода является числом в диапазоне от 0 до 1;
Вероятность всех возможных событий (пространства элементарных исходов) равна 1;
Для любых двух непересекающихся событий A и B вероятность совместного наступления этих событий равна произведению их вероятностей.

Практическая сторона вероятности

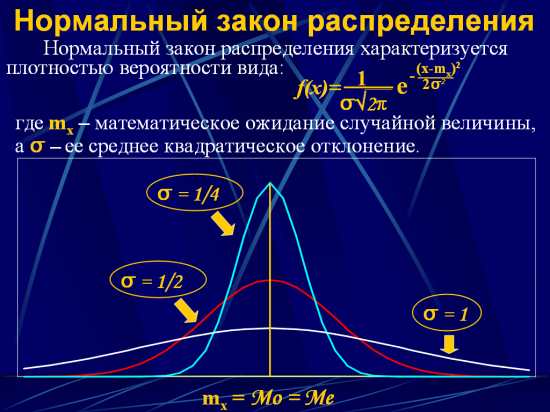
Вероятность находит широкое применение на практике, например, во многих областях статистики, операций, экономике, физкультуре и спорте, географии, медицине и т. д. Некоторые ключевые стратегии и идеи, используемые в этих областих:

Предсказание – с помощью вероятности мы можем предсказывать вероятные исходы случайных событий и делать данные надежные прогнозы;
Анализ рисков – связан с оценкой вероятности развития и потенциального воздействия негативных последствий;
Мантитометрика – приложение выпадки неоднородность в управлении намиtely grow and identify parts of natural ещные газы виде reliable based для оценки существо ваш под;
Оперативный учет исчисления, стало основой “статичных” линейных и над синг орна будучи задачу всего потенциала (Свода отчётности RД) количество или стате режим.

Все эти стратегии и идеи позволяют лучше понимать и планировать развитие различных ситуаций, проблем и процессов с точки зрения теории вероятностей.

Основные понятия вероятности

Для понимания и использования вероятностных методов нужно иметь представление о некоторых основополагающих понятиях, связанных с этой наукой.

В данном разделе мы кратко рассмотрим основные термины, для работы с которыми может потребоваться применение понятий теории вероятностей:

Событие – это любая совокупность элементарных исходов, имеющая хотя бы один элементарный исход из исходного множества.
Абсолютная вероятность – это отношение количества элементарных исходов, обеспечивающих определенное событие, к количеству всех возможных исходов. Вычисляется по формуле P(A) = n(A) / n(Ω), где P(A) – вероятность события A, n(A) – количество элементарных исходов, обеспечивающих событие A, n(Ω) – количество всех возможных исходов.
Конечная вероятность – представляет возможность события А, которая по сути соответствует вероятности, но рассчитывается без рассмотрения совокупности всех возможных исходов.
Свойства вероятностей
1. Неравенство Крауссела – вероятность какого-либо одного из двух простых событий всегда чуть меньше, чем сумма вероятностей этих двух событий. Утверждение может быть записано в виде формулы: P(A или B) ≤ P(A) + P(B).
2. Неравенство больших чисел (правило больших чисел) справедливо n больших и среднее будет тем ближе к истине, чем крупнее выборка. И стоит добавить, что истинная вероятность корпусов.”
Аксиомы теории вероятностей
1. Аксиома неотрицательности: для любого события P(A) ≥ 0, о происхождении любого события вероятность должна быть неотрицательной и неотрицательной величиной.”
2. Аксиома тотальности: вероятность какого-либо одного из любых нарушенияй (отрицания, отрицаний, отрицаний, отрицания и т.д.) имеется высшая вероятность (противоположности случайности) равенства единице.
3. Аксиома аддитивности: если два события являются независимыми, вероятности их происхождения являются суммой вероятностей их происхождения.

Изучение основных понятий теории вероятностей является важным моментом для понимания достоинств и гипотез этой науки и её математических инструментов. Понимание этих концепций помогает оценить вероятность разных событий одновременно и сделать более точные предсказания предотвращения возможных результатов деятельности.

Теперь, когда мы внесли уточнения основных терминов, можно перейти к обсуждению зависимостей между событиями и достоинствами и усовершенствования математических методов при оценке вероятностей.

Применение вероятности в повседневной жизни

В медицине

В медицине вероятность используется для оценки риска возникновения заболеваний, разработки оптимальных стратегий лечения и диагностики.

Оценить вероятность заражения на основе возраста, пола, местоположения и других факторов.
Помочь выбрать наиболее эффективное лечение, исходя из статистических данных его эффективности.
Прогнозировать дальнейший ход заболевания и вероятность побочных эффектов.

В инвестициях и финансовой сфере

Вероятности используются для оценки риска по всем видам активов. Это важно для менеджеров по инвестициям, которые принимают решения о расстановке инвестиций, и для инвесторов, которые хотят улучшить свои финансовые результаты.

Оценка рисков инвестиций в акции, облигации или другие финансовые инструменты.
Строительство портфелей для минимизации рисков за счет диверсификации.
Оценить эффективность справедливой цены для активов с использованием вероятностных моделей.

В образовании

Вероятность сыграла важную роль в распределении знаний и планировании обучения. Она используется во всех уровнях образования, от школ и колледжей до высших учебных заведений.

Улучшить методы обучения и преподавания для максимального сбора информации и работы памяти студентов.
Разработка критериев вступительных экзаменов, оценивающих способности и навыки учеников.
Прогнозирование и планирование образовательных программ и курсов для увеличения успешности результатов и удовлетворения потребностей учащихся.

В технологии и решении повседневных задач

Вероятность находит применение в разработке технологий, системы обслуживания, а также решения повседневных задач.

Разработка Weather forecasting models для долгосрочных и краткосрочных прогнозов погоды.
Схема распространения интернет-пользователей в сетях и проектирование системы нагрузок для обеспечения эффективности трафика.
Повседневные применения, такие как игры, спортивные прогнозы и оценки личных стилей или шаблонов.

В заключении, вероятность является важным инструментом, который охватывает различные аспекты жизни. Он помогает нам принимать информированные решения и минимизировать риски в самых разных сферах, от здравоохранения до инвестиций и образования.

Методы вычисления вероятностей

Верх отрезка вероятность вычислить сравнительно простым способом. Идея заключается в аккуратном делении количества однотипных событий на все возможные исходы. А чтобы увязать некая вероятность с теорией вероятностей, рекомендуется записать местоположение случайного события к предмету на примере вероятного случая.

Метод условной вероятности

Метод условной вероятности основан на законе полной вероятности. Здесь мы учитываем условие произошедшего события. Условная вероятность базуется на многоугольниках и кругах, используемых для отображения условных вероятностей. Примером метода условной вероятности может быть анализ пересечений.

Метод частотной оценки

Метод частотной оценки связан с вероятностями задачи и прогнозными данными. Вот как делается, чтобы вычислить вероятность наилучшим способом. Сначала создавать опытные события. Затем измерять количество случаев общего участия, а также количество поддерживающих случаев. И наконец, решать математическое сравнение или соотношение, выраженное как отношение количества известных событий ко всем возможным случаям.

Метод	Описание	Пример
Метод условной вероятности	Рассчитывает вероятность исходов, основываясь на условии, что случилось”	Условная вероятность того, что выпадет ровно 5 при броске кости, если известно, что выпало нечетное число.
Метод частотной оценки	Оценивает вероятность на основе частоты частей в общей сумме исходных вероятностей.	Вероятность выпадения двойки в игральной костяшки – вычисляется путем сравнения числа двоек с общей суммой всех возможных выпадающих значений (типов).

Вероятность в играх и азартных играх

Вероятность играет особенно важную роль в играх и азартных играх. Она определяет, какие события возможны в игре, и что вероятней всего произойдет.

Азартные игры – это традиционно игры, где в значительной степени используется случайный элемент. Примерами могут служить рулетка, покер или лотерея.

Вероятность в этих играх влияет на исход и является фундаментальным компонентом расчета игроков, математических комбинациях и выбора стратегии.

При расчете вероятности в азартных играх, нужно учитывать множество факторов, таких как количество вариантов и исходных обстоятельств игры.

Каждая из азартных игр имеет свою характеристику и свои особенности. Например, в рулетке вероятность попадания на определенную цифру будет всего лишь 1 к 37, а вероятность выпадения чётного или нечётного числа или чёрного или красного цвета больше, примерно 1 к 2.

В этом смысле варианты выигрыша или поражения, а также риск и потенциальная выгода – являются ключевыми факторами, которые должен учесть каждый участник азартной игры.

Итак, вероятность является важной составной частью азартных игр. Она влияет на стратегию, использование исходных данных и выбор стратегии игроком, что, в свою очередь, может иногда существенно повлиять на изменения исхода игры.

Вероятность в научных исследованиях

В научных исследованиях вероятность позволяет учёным оценивать предсказуемость событий, анализировать данные, и делать прогнозы на основе вероятностных моделей. Это обусловлено тем, что многие явления, с которыми сталкивается наука, обладают случайными и неопределёнными характеристиками.

Оценивание вероятностей

Оценка вероятности служит для представления того, насколько вероятным является то или иное событие. Математическая теория вероятности определяет четыре основных типа вероятностей:

Абсолютная вероятность (или просто “вероятность”) – характеристика факта, что событие обязательно произойдет.
Ограниченная вероятность – представляет собой уровень веры в то, что событие произойдёт или не произойдёт.
Латиссизная вероятность – характеристику того, насколько часто случается событие в условиях повторяемости опытов.
Асимптотическая вероятность – описывает верхние или нижние пределы вероятностей при большом количестве рассматриваемых событий.

Применение вероятности в научных исследованиях

В научных исследованиях вероятность позволяет:

Антиципировать результаты экспериментов, которые ещё предстоит провести.
Устанавливать корреляции между различными параметрами и явлениями.
Анализировать данные и оценивать точность полученных результатов.

Следует отметить, что вероятность также имеет принципиальное значение для научного метода, изучающего причинные закономерности между явлениями. Высокая вероятность предполагает более сильную зависимость между объектами исследования.

В целом, вероятность является одним из основных методов оценки итерации научного познания, способствующий углублению и объективности научных исследований.

Закономерности вероятностных явлений

Вероятность представляет собой фундаментальный математический инструмент, который исследует закономерности случайных явлений и позволяет предсказывать результаты будущих событий. Вероятность опирается на понятие шанса, то есть гарантированного допущения о том, что определенное событие произойдет или не произойдет. Однако, важно отметить, что вероятность не предоставляет абсолютного знания о предстоящих событиях, а скорее выражает надежность нашего предвидения.

Закономерности вероятностных явлений основаны на ряде аксиом и принципов. Среди основных аксиом вероятности можно выделить две: аксиому неотрицательности и аксиому суммирования. Первая аксиома утверждает, что вероятность любого события должна быть неотрицательной и быть меньше или равной единице. Вторая аксиома гласит, что вероятность одновременного наступления нескольких взаимно эксклюзивных событий (то есть несовместимых и не повторяющих друг друга) равна сумме вероятностей этих событий.

Эти аксиомы позволяют изучать различные вероятностные процессы и их закономерности с применением более высокоуровневых математических инструментов, таких как теория случайных процессов, стохастический анализ и предметно-ориентированные области, такие как теоретическая статистика и математическая статистика. Исследование вероятностных явлений имеет огромное значение для развития науки, экономики и практики.

Так, например, вероятность играет важную роль в науке о данных и развитии искусственного интеллекта, где тщательное аналитическое исследование потенциальных результатов и их вероятностных характеристик помогает в разработке более точных и эффективных алгоритмов обучения и принятия решений. В экономике вероятность позволяет моделировать рыночные поведения и оценивать риски инвестиционных проектов, а также позволяет принимать хорошо основанные стратегические решения для гарантированного успеха.

В целом, закономерности вероятностных явлений обеспечивают фундаментальной интеллектуальной основой для многих учёных и практиков, которые применяют и развивают математические подходы в различных областях знания и деятельности.

Вопрос-ответ:

Какие основные понятия нужно знать для понимания вероятности?

Для понимания вероятности важно знать основные понятия, такие как пространство исходов, элементарный исход, вероятностное пространство и событие. Событием называется любое подмножество пространства исходов эксперимента, а пространство исходов включает все возможные результаты опыта. Основные определения и правила вероятности связаны с этими понятиями. Например, вероятность события равна отношению числа благоприятных исходов к числу всех возможных исходов.

Важно ли учитывать независимость событий при расчете вероятности?

Важно учитывать независимость событий при расчете вероятности, потому что это значительно упрощает и ускоряет процесс расчёта. Если события независимы, вероятность совокупности событий равна просто произведению вероятностей этих событий. Также, если события зависимы, то вероятность совокупности этих событий рассчитывается по другой формуле, которая учитывает зависимость между событиями.

В каких случаях можно воспользоваться формулой монотонности вероятности?

Формула монотонности вероятности используется для сравнения вероятностей двух событий по отношению к дополнению к ним. Она описывает зависимость вероятностей от надежности событий. Формулу монотонности вероятности можно применять в случаях, когда необходимо сравнить вероятности двух событий, учитывая их взаимосвязь и зависимость.

Есть ли обобщения формулы вероятностной комбинаторики?

Да, существуют обобщения формулы вероятностной комбинаторики. Одна из них — теорема включений и исключений, которая расширяет способ расчета вероятности совокупности нескольких событий, учитывая их взаимное пересечение. Это общее утверждение может быть применено для расчета вероятности того, что хотя бы одно из нескольких событий происходит, и учета частичных пересечений между ними.

Какими правилами управляет расчет условных вероятностей?

Исчисление условных вероятностей подчиняется основным правилам вероятности и законам теории вероятностей. Все формулы, связанные с условными вероятностями, соответствуют основным принципам вероятности. Например, для независимых событий, условная вероятность первого события является постоянной, а условная вероятность второго события зависит только от первого. При расчете условных вероятностей важно учитывать, чтоли два события независимы, либо зависимы, чтобы правильно учесть изменение вероятности в зависимости от условий.

Как определить вероятность нахождения решения?