Вершины эллипса как найти онлайн - Сайт, где вы сможете решить свои вопросы

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

вершины:9x^2+4y^2=1
вершины:16x^2+25y^2=100
вершины:25x^2+4y^2+100x-40y=400
вершины:frac{(x-1)^2}{9}+frac{y^2}{5}=100
Показать больше

Описание

Пошаговый расчет вершин эллипса по заданному уравнению

ellipse-vertices-calculator

Блог-сообщения, имеющие отношение к Symbolab

Practice, practice, practice

Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Here is a simple calculator to solve ellipse equation and calculate the elliptical co-ordinates such as center, foci, vertices, eccentricity and area and axis lengths such as Major, Semi Major and Minor, Semi Minor axis lengths from the given ellipse expression. An ellipse is a figure consisting of all points for which the sum of their distances to two fixed points, (foci) is a constant.

Solve Ellipse Equation

Code to add this calci to your website

Solving Ellipse Equation is just the inverse of finding the ellipse expression from the given elliptical co-ordinates such as center, foci, vertices, eccentricity and area.

Источник

Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.

Что такое эллипс и фокусное расстояние

Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .

Обозначим фокусы эллипса $F_{1}$ и $F_{2}$ . Допустим, что расстояние $F_{1}{F_{2}}$ = – фокусное расстояние.

Рис. 1

$F_{1}, F_{2}$ – фокусы .

$F_{1} = (c, 0)$ ; $F_{2} = (- c ; 0)$ ,

– половина расстояния между фокусами;

– большая полуось;

– малая полуось.

Теорема:

Фокусное расстояние и полуоси связаны соотношением:

Если точка находится на пересечении эллипса с вертикальной осью, $r_{1} + r_{2} = 2 * sqrt{b^2 + c^2}$ (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, $r_1} + r_{2} = a - c + a + c$ . Так как по определению сумма $r_{1} + r_2}$ – постоянная величина, то приравнивая получается:

$a^2 = b^2 + c^2to{r_{1} + r_{2} = 2a$ .

Уравнение эллипса

Уравнение элиппса бывает двух видов:

Каноническое уравнение эллипса.
Параметрическое уравнение эллипса.

Сначала рассмотрим каноническое уравнение эллипса:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:

$1 = {x^2over{a^2}} + {y^2over{b^2}}$

Если центр эллипсa смещен в точку с координатами $(x_{0}, y_{0})$ тогда уравнение:

$1 = {(x - x_{0})^2over{a^2}} + {(y - y_{0})^2over{b^2}}$

Чтобы получить каноническое уравнение эллипса, разместим $F_{1}$ и $F_{2}$ на оси симметричной к началу координат. Тогда у фокусов будут такие координаты $F_{2}(-c, 0)$ и $F_{2}(c, 0)$ (см. рис. 2).

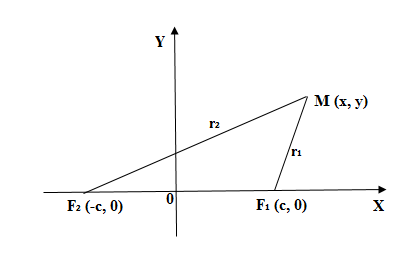
Пусть – произвольная точка эллипса. Обозначим через $r_{2}$ и $r_{1}$ – расстояние от точки к фокусам. Согласно с определением эллипса:

$r_{1} + r_{2} = 2a$

(1)

Рис. 2

Подставим в (1) $r_{1} = F_{1}M = sqrt{(x - c)^2 + (y - 0)^2}$ , $r_{2} = sqrt{(x + c)^2 + y^2}$ и освободимся от иррациональности, подняв обе части к квадрату, получим:

$r_{2} = 2a - r_{1}tosqrt{(x + c)^2 + y^2} = 2a - sqrt{(x - c)^2 + y^2}}to{x^2 + 2cx + c^2 + y^2} = 4a^2 - 4asqrt{(x - c)^2) + y^2} + x^2 - 2cx + c^2 + y^2to{4a}sqrt{(x - c^2 + y^2} = 4a^2 - 4cxarrowvert:4$

$asqrt{(x - c)^2 + y^2} =a^2 - cx$

(подносим к квадрату обе части): $to{a^2x^2 - 2ca^2x + a^2c^2 + a^2y^2} = {a^4 - 2ca^2x + c^2x^2to{(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)arrowvert:a^2(a^2 - c^2)$ ,

${x^2over{a^2}} + {y^2over{a^2 - c^2}} = 1$

Обозначим: , получаем каноническое уравнение эллипса:

${x^2over{a^2}} + {y^2over{b^2}} = {1}$

(2)

Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из $Delta{F_{1}}MF_{2}$ у нас получается $F_{2}M + F_{1}M > F_{1}F_{2}to{r_{1} + r_{2}} > 2c$ . Так как $r_{1} + r_{2} = 2a$ , тогда , и поэтому .

Для построения эллипса обратим внимание, что если точка $M_{1}(x, y)$ принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки $M_{2}(-x, y), M_{3}(-x, -y), M_{4}(x, -y)$ тоже удовлетворяют это уравнение: из

${x^2over{a^2}} + {y^2over{b^2}} = 1to{(pm{x})^2over{a^2}} + {(pm{y})^2over{b^2}} = {1}$ .

Точки $M_{1}, M_{2}, M_{3}, M_{4}$ – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.

Из уравнения (2) находим $y = pm{{b}over{a}}sqrt{a^2 - x^2$ , для первой четверти ${y} = {bover{a}}sqrt{a^2 - x^2}$ .

Если , тогда . Если же , тогда . Точки $A_{1}(a, 0)$ и $B_{1}(0, b)$ , а также симметричные с ними $A_{2}(-a, 0)$ , $B_{2}(0, -b)$ – вершины эллипса, точка – центр эллипса, $A_{1}A_{2}$ = большая ось, $B_{1}B_{2} = 2b$ – малая ось эллипса.

Если первой четверти, тогда из $y = {bover{a}}sqrt{a^2 - x^2$ получается, что при возрастании от к значение падает от к . (рис. 3)

Параметрическое уравнение выглядит так:

$left{ begin{aligned} x = a{cos}alpha\ y = b{sin}alpha end{aligned}quad {0leqalpha < 2pi right$

Основные свойства эллипса

Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.

1. Угол между касательной к эллипсу и фокальным радиусом $r_{1}$ равен углу между касательной и фокальным радиусом $r_{2}$ .

2. Уравнение касательной к эллипсу в точке с координатами $(x_{M}, y_{M})$ :

$1 = {x x_{M}over{a^{2}}} + {y y_{M}over{b^{2}}}$ .

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).

4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами $F_{1}$ и $F_{2}$ у треугольника , тогда выполняется соотношение:

= ${{overline{F_{1}A} * overline{F_{2}A}}over{overline{CA} * overline{AB}}} + {{overline{F_{1}B} * overline{F_{2}B}}over{overline{AB} * overline{BC}}} + {{overline{F_{1}C} * overline{F_{2}C}}over{overline{BC} * overline{CA}}}$

Эксцентриситет эллипса

Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается

Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда $c = {sqrt{a^2 + b^2}} = 0to{varepsilon = 0}$ – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:

$left{ begin{aligned} r_{1} = a - varepsilon{x},\ r_{2} = a + varepsilon, end{aligned} quad{xin[-a, a]. right$

Рис. 3

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим $c = {sqrt{a^2 + b^2}}$ – полуфокусное расстояние.

Строим фокусы $F_{1}$ и $F_{2}$ на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках $F_{1}$ и $F_{2}$ . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Примеры решения задач

Задача

Задан эллипс уравнением ${x^2over{25}} + {y^2over{9}} = 1$ и точки $M_{0}(4; 1,8), M_{1}(3; 2,4)$ . Необходимо:

убедиться, что точки $M_{0}$ и $M_{1}$ лежат на эллипсе;
найти полуоси эллипса и координаты его фокусов;
найти расстояние от точки $M_{0}$ к фокусам;
убедиться, что сумма этих расстояний равна длине большой оси;
найти эксентриситет эллипса.

Решение

1. Подставим координаты точки $M_{0}$ в левую часть уравнения эллипса:

${x^2over{25}} + {y^2over{9}} = {4^2over25}} + {1,8 * 1,8over{9}} = {16over25}} + {36over{100}} = {16over{25}} + {9over25}} = 1$ – точка $M_{0}$ лежит на эллипсе. Аналогично для $M_{1}(3; 2,4)$ :

точка $M_{1}$ лежит на эллипсе.

2. С канонического ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ и данного уравнения ${x^2over{25}} + {y^2over{9}} = 1$ эллипса выходит: $a^2 = {25},quad{b^2 = 9}to{a = 5, b = 3}.$ Из равенства получается:

$b^2 = a^2 - c^2to {c^2 = a^2 - b^2 = 25 - 9} = {16}to{c = 4}$ – полуфокусное расстояние. Координаты фокусов $F_{1}(4; 0)$ и $F_{2}(-4; 0)$ .

3. Найдём фокальные радиусы точки $M_{0}$ :

$r_{2} = F_{2}M_{0} = sqrt{(4 - (-4))^2 + 1,8^2} = sqrt{64 + 3,24} = sqrt{67,24} = 8,2$

$r_{1} = F_{1}M_{0} = sqrt{(4 - 4)^2 + 1,8^2} = 1,8.$

4. Найдём сумму $r_{1} + r_{2} = 1, 8 + 8.2 = 10 = 2 * 5 = 2a$ , что отвечает определению эллипса.

5. Эксцентриситет находится по формуле .

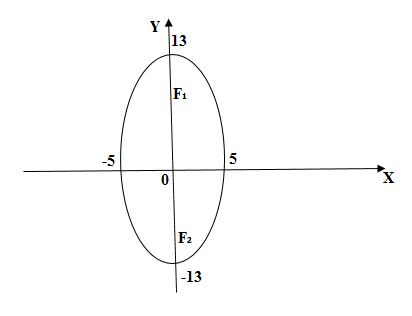
Задача

Найти оси, вершины и фокусы эллипса

Решение

Сведём обычное уравнение к каноническому:

$169x^2 + 25y^2 - 4225 = 0to{x^2over{25}} + {y^2over{169}} = 1$

, $b^2 = 169to{a = 5, b = 13}$ . Вершины эллипса в точках $A_{1}(5, 0)$ , $B_{1}(0, 13)$ , $A_{2}(-5, 0)$ , $B_{2}(0, -13)$ . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние $c = sqrt{b^2 - a^2} = sqrt{169 - 25} = sqrt{144} = 12$ .

Фокусы в точках $F_{1}(0, 12)$ и $F_{2}(0, -12)$ . (см. рис. 3)

Рис. 4

Найти оси, вершины и фокусы эллипса $25x^2 + 144y^2 = 3600quad{:}arrowvertto{25x^2over{3600}} + {144y^2over{3600}} = {1}to{x^2over{144}} + {y^2over{25}} = {1}$ или ${X^2over{12^2}} + {y^2over{5^2}} = {1}$ . Построить эллипс.

Сравнивая последнее уравнение с уравнением (2), у нас получается:

, $b^2 = 5^2to{a = 12, b = 5}$ . Откуда находим оси эллипса: , и координаты вершин: $A_{1}(12, 0)$ , $A_{2} (-12, 0)$ , $B_{1}(0, 5)$ , $B_{2}(0, -5)$ . Дальше из формулы:

$b^2 = a^2 - c^2to{c^2 = a^2 - b^2 = 144 - 25 = 119}to{c = sqrt{119}}approx{10,91}$ . Значит, фокусами эллипса есть точки: $F_{1}(sqrt{119}, 0)$ и $F_{2}(-sqrt{119}, 0)$ . Для построения эллипса отложим на осях и вершины $A_{1}, B_{1}, A_{2}, B_{2}$ соответственно соединим их плавной линией, (см. задачу 1).

Замечание! Если в каноническом уравнении ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда $c = sqrt{b^2 - a^2}$ .

Источник

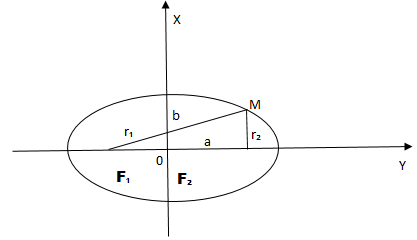
Определение эллипсa

Определение.

Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F₁ и F₂ равна постоянной величине. Точки F₁ и F₂ называют фокусами эллипса.

F₁M₁ + F₂M₁ = F₁M₂ + F₂M₂ = A₁A₂ = const

Элементы эллипсa

F₁ и F₂ – фокусы эллипсa

Оси эллипсa.

А₁А₂ = 2a – большая ось эллипса (проходит через фокусы эллипса)

B₁B₂ = 2b – малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)

a – большая полуось эллипса

b – малая полуось эллипса

O – центр эллипса (точка пересечения большей и малой осей эллипса)

Вершины эллипсa A₁, A₂, B₁, B₂ – точки пересечения эллипсa с малой и большой осями эллипсa

Диаметр эллипсa – отрезок, соединяющий две точки эллипса и проходящий через его центр.

Фокальное расстояние c – половина длины отрезка, соединяющего фокусы эллипсa.

Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.

Фокальные радиусы эллипсa r₁, r₂ – расстояния от точки на эллипсе до фокусов.

Радиус эллипсa R – отрезок, соединяющий центр эллипсa О с точкой на эллипсе.

R =	ab	=	b
√a²sin²φ + b²cos²φ	√1 – e²cos²φ

где e – эксцентриситет эллипсa, φ – угол между радиусом и большой осью A₁A₂.

Фокальный параметр эллипсa p – отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:

Коэффициент сжатия эллипсa (эллиптичность) k – отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:

k = √1 – e²

где e – эксцентриситет.

Сжатие эллипсa (1 – k ) – величина, которая равная разности между единицей и эллиптичностью:

Директрисы эллипсa – две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии

от центра эллипса. Расстояние от фокуса до директрисы равно

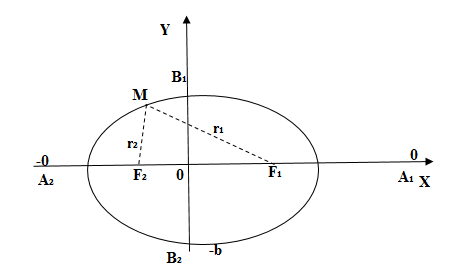
Основные свойства эллипсa

1. Угол между касательной к эллипсу и фокальным радиусом r₁ равен углу между касательной и фокальным радиусом r₂ (Рис. 2, точка М₃).

2. Уравнение касательной к эллипсу в точке М с координатами (x_M, y_M):

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)

4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами F₁ и F₂ у треугольник ∆ ABC, то будет выполнятся следующее соотношение:

1 =	F₁A ∙ F₂A	+	F₁B ∙ F₂B	+	F₁C ∙ F₂C
CA ∙ AB	AB ∙ BC	BC ∙ CA

Уравнение эллипсa

Каноническое уравнение эллипсa:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:

Если центр эллипсa О смещен в точку с координатами (x_o, y_o), то уравнение:

1 =	(x – x_o)²	+	(y – y_o)²
a²	b²

Параметрическое уравнение эллипсa:

{	x = a cos α	де 0 ≤ α < 2π
y = b sin α

Радиус круга вписанного в эллипс

Круг, вписан в эллипс касается только двух вершин эллипсa B₁ и B₂. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB₁:

r = b

Радиус круга описанного вокруг эллипсa

Круг, описан вокруг эллипсa касается только двух вершин эллипсa A₁ и A₂. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA₁:

R = a

Площадь эллипсa

Формула определение площади эллипсa:

S = πab

Площадь сегмента эллипсa

Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):

S =	πab	–	b	(	x	√	a² – x² + a² ∙ arcsin	x	)
2	a	a

Периметр эллипсa

Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:

L ≈ 4	πab + (a – b)²
a + b

Длина дуги эллипсa

Формулы определения длины дуги эллипсa:

1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:

	t₂
l =	∫	√a²sin²t + b²cos²t dt
	t₁

2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:

	t₂
l =	∫	√1 – e²cos²t dt, e < 1
	t₁

Источник

Номер Строки

Solve Ellipse Equation

Что такое эллипс и фокусное расстояние

Уравнение эллипса

Основные свойства эллипса

Эксцентриситет эллипса

Примеры решения задач

Определение эллипсa

Элементы эллипсa

Основные свойства эллипсa

Уравнение эллипсa

Каноническое уравнение эллипсa:

Параметрическое уравнение эллипсa:

Радиус круга вписанного в эллипс

Радиус круга описанного вокруг эллипсa

Площадь эллипсa

Площадь сегмента эллипсa

Периметр эллипсa

Длина дуги эллипсa

Формулы определения длины дуги эллипсa:

Вам также может понравиться

Как найти любимую женщину после 50 лет

Как найти голых мужиков

Как найти автостраховку в электронном виде

Добавить комментарий Отменить ответ