Вершины это как найти графов

Теория графов. Термины и определения в картинках

В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.

Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов. 

Граф – это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.

Например, граф на рисунке состоит из 8 вершин и 8 рёбер.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними – за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.

В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус  “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов. 

Вершина – точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.

Ребро – неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге – не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.

Инцидентность – вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру. 

Смежность вершин – две вершины называются смежными, если они инцидентны одному ребру.

Смежность рёбер – два ребра называются смежными, если они инцедентны одной вершине.

Говоря проще – две вершины смежные, если они соединены ребром, два ребра смежные – если они соединены вершиной.

Петля – ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине. 

Псевдограф – граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название. 

Кратные рёбра – рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.

Мультиграф – граф с кратными рёбрами.

Псевдомультиграф – граф с петлями и кратными рёбрами.

Степень вершины – это количество рёбер, инцидентных указанной вершине. По-другому – количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.

Изолированная вершина – вершина с нулевой степенью.

Висячая вершина – вершина со степенью 1.

Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа. 

Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.

Полный граф – это граф, в котором каждые две вершины соединены одним ребром. 

Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N – каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N – 1) / 2.

Регулярный граф – граф, в котором степени всех вершин одинаковые.

Двудольный граф – если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.

Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.

Если это невозможно сделать, то граф называется “непланарным”.

Минимальные непланарные графы – это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.

Путь или Маршрут – это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.

Длина пути – количество рёбер в пути.

Цепь – маршрут без повторяющихся рёбер.

Простая цепь – цепь без повторяющихся вершин.

Цикл или Контур – цепь, в котором последняя вершина совпадает с первой. 

Длина цикла – количество рёбер в цикле.

Самый короткий цикл – это петля.

Цикл Эйлера – цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.

Цикл Гамильтона – цикл, проходящий через все вершины графа по одному разу. Другими словами – это простой цикл, в который входят все вершины графа.

Взвешенный граф – граф, в котором у каждого ребра и/или каждой вершины есть “вес” – некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути. 

Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса – “Алгоритмы и структуры данных”.

Связный граф – граф, в котором существует путь между любыми двумия вершинами.

Дерево – связный граф без циклов.

Между любыми двумя вершинами дерева существует единственный путь.

Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.

Лес – граф, в котором несколько деревьев.

Ориентированный граф или Орграф – граф, в котором рёбра имеют направления.

Дуга – направленные рёбра в ориентированном графе.

Полустепень захода вершины – количество дуг, заходящих в эту вершину.

Исток – вершина с нулевой полустепенью захода.

Полустепень исхода вершины – количество дуг, исходящих из этой вершины

Сток – вершина с нулевой полустепенью исхода.

Компонента связности – множество таких вершин графа, что между любыми двумя вершинами существует маршрут.

Компонента сильной связности – максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.

Компонента слабой связности – максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).

Мост – ребро, при удалении которого, количество связанных компонент графа увеличивается.

Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи – дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.

• Узнать о курсе подробнее

• Записаться на интенсив: “Алгоритм сжатия данных – код Хаффмана. Создание Архиватора.”. День 1

• Записаться на интенсив: “Алгоритм сжатия данных – код Хаффмана. Создание Архиватора.”. День 2

Вершинa графа — фундаментальная понятие теории графов.
Неориентированный граф состоит из множества вершин и множества рёбер (неупорядоченных пар вершин), в то время как ориентированный граф состоит из множества вершин и множества дуг (упорядоченных пар вершин). На рисунках, представляющих граф, вершина обычно обозначается кружком с меткой, ребро — линией, дуга — стрелкой, соединяющей вершины.

С точки зрения теории графов, вершины рассматриваются как лишённые характерных черт неделимые объекты, хотя они могут представлять некоторые структуры, зависящие от задачи, из которой возник граф. Например семантическая сеть — это граф, в котором вершины представляют понятие класса объектов.

Две вершины, образующие ребро, называются конечными вершинами ребра и говорят, что ребро инцидентно вершинам.
Говорят, что вершина w смежна другой вершине v, если граф содержит ребро (v, w). Окрестностью вершины v называется порождённый подграф, образованный всеми вершинами, смежными v.

Типы вершин[править | править код]

Степенью вершины графа называется число рёбер, инцидентных ей. Вершина называется изолированной, если её степень равна нулю. То есть это вершина, не являющаяся конечной ни для какого ребра. Вершина называется листом (или висячей), если имеет степень единица. В ориентированном графе различают полустепень исхода (число исходящих дуг) и полустепень захода (число входящих рёбер). Источником называется вершина с нулевой полустепенью захода, а вершина с нулевой степенью исхода называется стоком.

Шарниром называется вершина, удаление которой приводит к увеличению компонент связности графа. Вершинным сепаратором называется набор вершин, удаление которых приводит к увеличению компонент связности графа. Вершинно k-связный граф — это граф, в котором удаление менее k вершин всегда оставляет граф связным. Независимым множеством называется множество вершин, никакие две из которых не являются смежными, а вершинным покрытием называется множество вершин, которое включает хотя бы одну конечную вершину любого ребра графа. Векторным пространством вершин^[en] графа называется векторное пространство, имеющее в качестве базиса векторы, соответствующие вершинам графа (над полем чисел {0, 1})^[1][2].

Граф называется вершинно-транзитивным если он имеет симметрии, которые переводят любую вершину в любую другую вершину. В контексте перечисления графов и изоморфизма графов важно различать помеченные вершины и непомеченные вершины . Помеченная вершина — это связанная с вершиной дополнительная информация, которая позволяет отличить её от других помеченных вершин. Два графа можно считать изоморфными только если изоморфизм переводит вершины в вершины, имеющие те же метки. Непомеченные вершины могут при этом переводиться в другие вершины, основываясь только на смежности и не используя дополнительную информацию.

Вершины графа аналогичны вершинам многогранника, но это не то же самое — скелет^[en] многогранника образует граф, вершины которого являются вершинами многогранника, но вершины многогранника имеют дополнительную структуру (геометрическое местоположение), которая игнорируется в теории графов. Вершинная фигура многогранника аналогична окрестности вершины графа.

См. также[править | править код]

• Узел (информатика)
• Теория графов
• Глоссарий теории графов

Примечания[править | править код]

Ссылки[править | править код]

• Giorgio Gallo, Stefano Pallotino. Shortest path algorithms (англ.) // Annals of Operations Research. — 1988. — Vol. 13, iss. 1. — P. 1—79. — doi:10.1007/BF02288320.
• К. Берж^[en]. Теория графов и её применение. — Москва: издательство Иностранной литературы, 1962.
• Gary Chartrand. Introductory graph theory. — New York: Dover, 1985. — ISBN 0-486-24775-9.
• Norman Biggs, E. H. Lloyd, Robin J. Wilson. Graph theory, 1736—1936. — Oxford [Oxfordshire]: Clarendon Press, 1986. — ISBN 0-19-853916-9.
• Frank Harary. Graph theory. — Reading, Mass.: Addison-Wesley Publishing, 1969. — ISBN 0-201-41033-8.
• Frank Harary, Edgar M. Palmer,. Graphical enumeration. — New York: Academic Press, 1973. — ISBN 0-12-324245-2.
• Weisstein, Eric W. Graph Vertex (англ.) на сайте Wolfram MathWorld.

 

Теория графов

В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.

Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.

Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.

Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.

Давайте на примере.

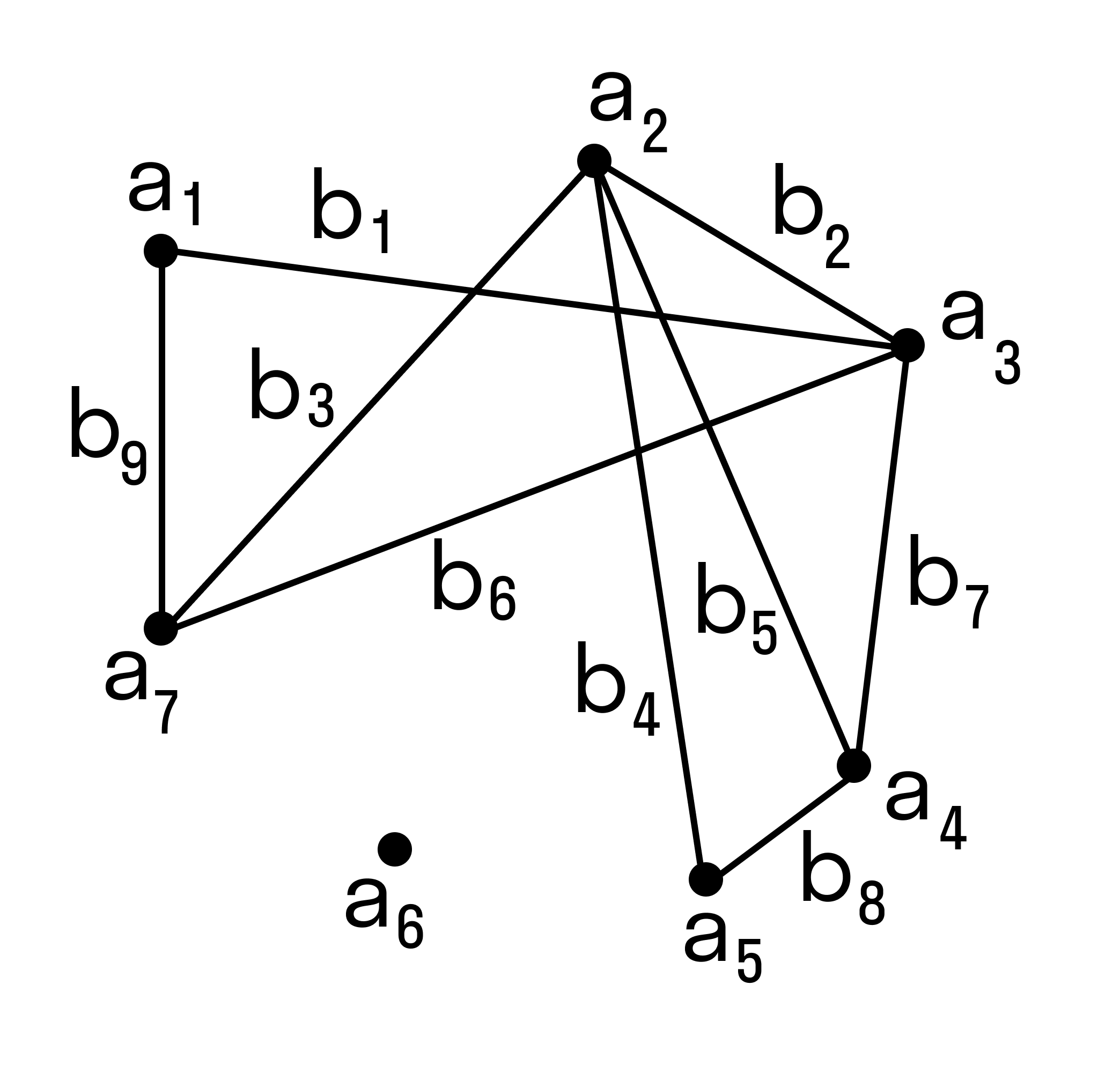
Пусть множество A = {a1, a2, … an} — это множество людей, и каждый элемент отображен в виде точки. Множество B = {b1, b2, … bm} — множество связок (прямых, дуг или отрезков).

На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.

Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:

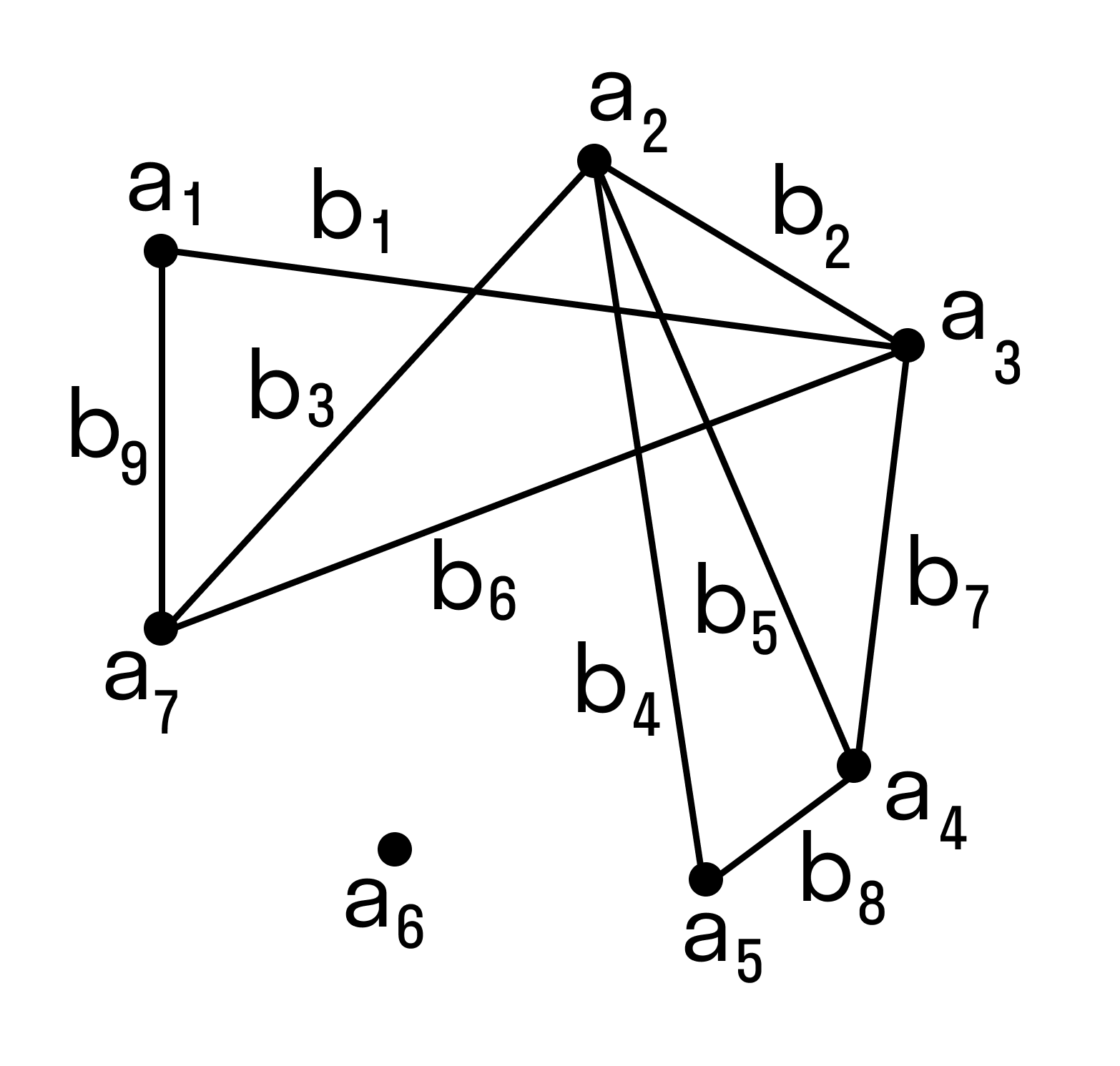
В данном случае точки — это вершины графа, а связки — рёбра графа.

Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.

Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.

Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.

Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.

Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.

Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.

Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.

 

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Основные понятия теории графов

Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.

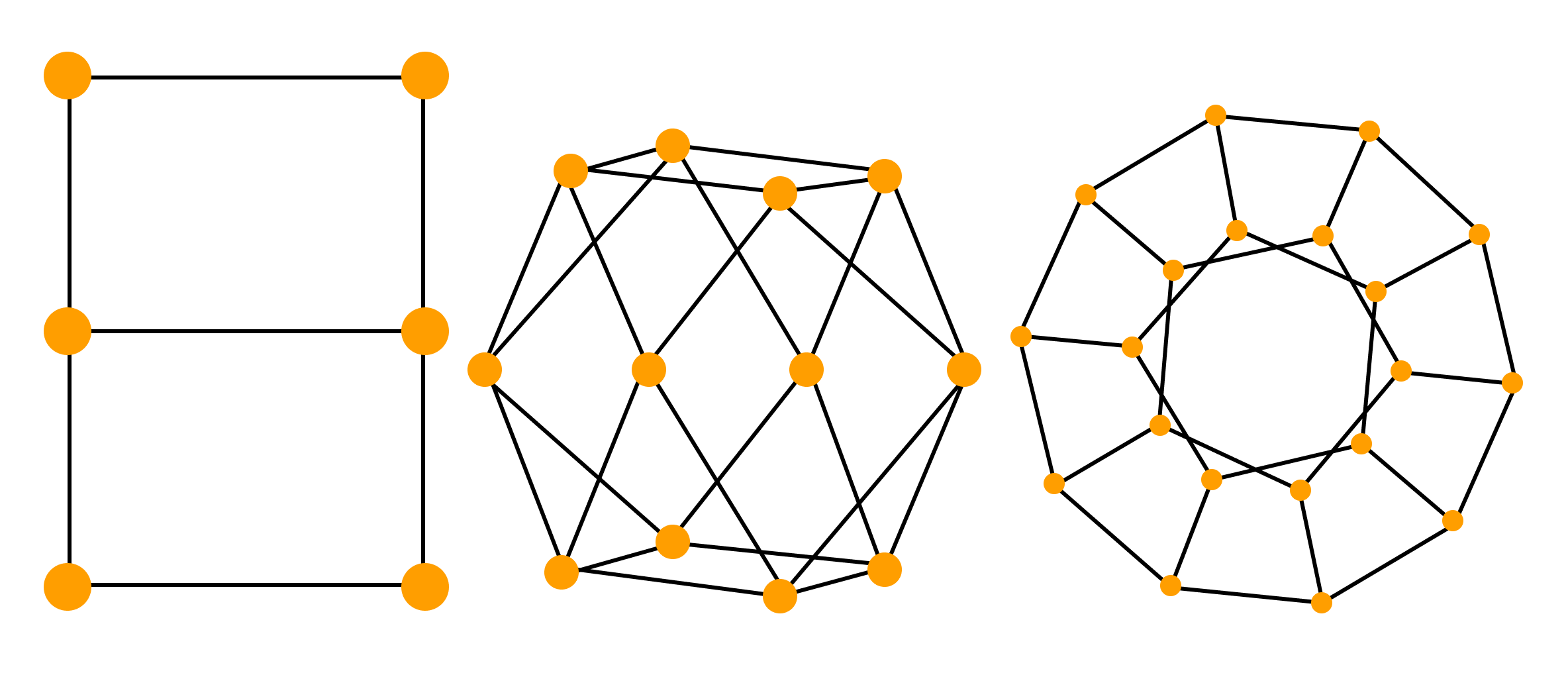
• Два ребра называются смежными, если у них есть общая вершина.
• Два ребра называются кратными, если они соединяют одну и ту же пару вершин.
• Ребро называется петлей, если его концы совпадают.
• Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).
• Вершина называется изолированной, если она не является концом ни для одного ребра.
• Вершина называется висячей, если из неё выходит ровно одно ребро.
• Граф без кратных ребер и петель называется обыкновенным.

Доказательство леммы о рукопожатиях

Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.

Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).

Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.

Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.

Как рассуждаем:

Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.

Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.

Как рассуждаем:

Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.

Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.

Путь и цепь в графе

Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Циклом называют путь, в котором первая и последняя вершины совпадают.

Путь или цикл называют простым, если ребра в нем не повторяются.

Если в графе любые две вершины соединены путем, то такой граф называется связным.

Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.

Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.

Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:

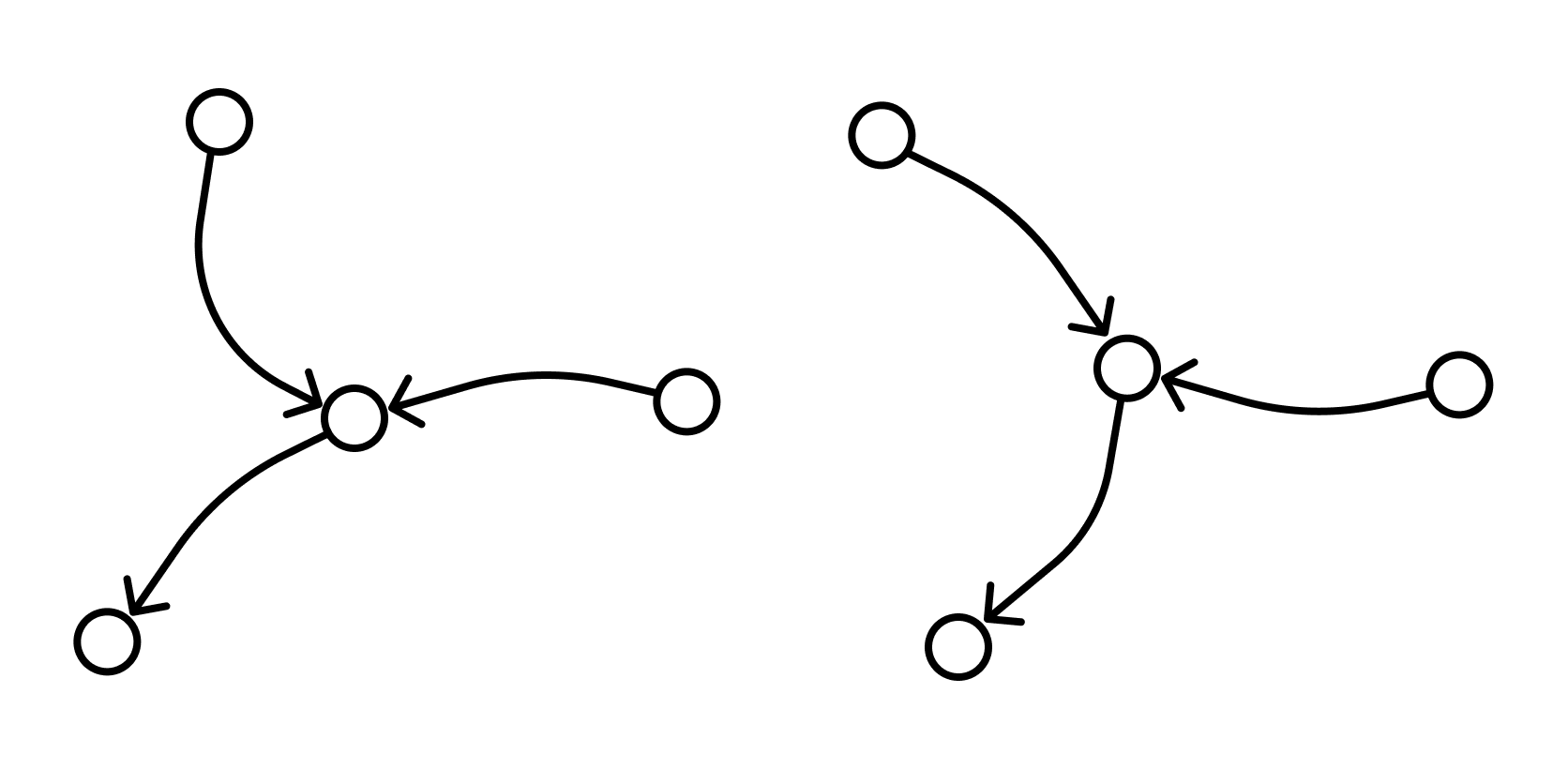
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.

Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.

 

Визуализация графовых моделей

Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.

Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.

Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.

Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.

Виды изобразительных соглашений:

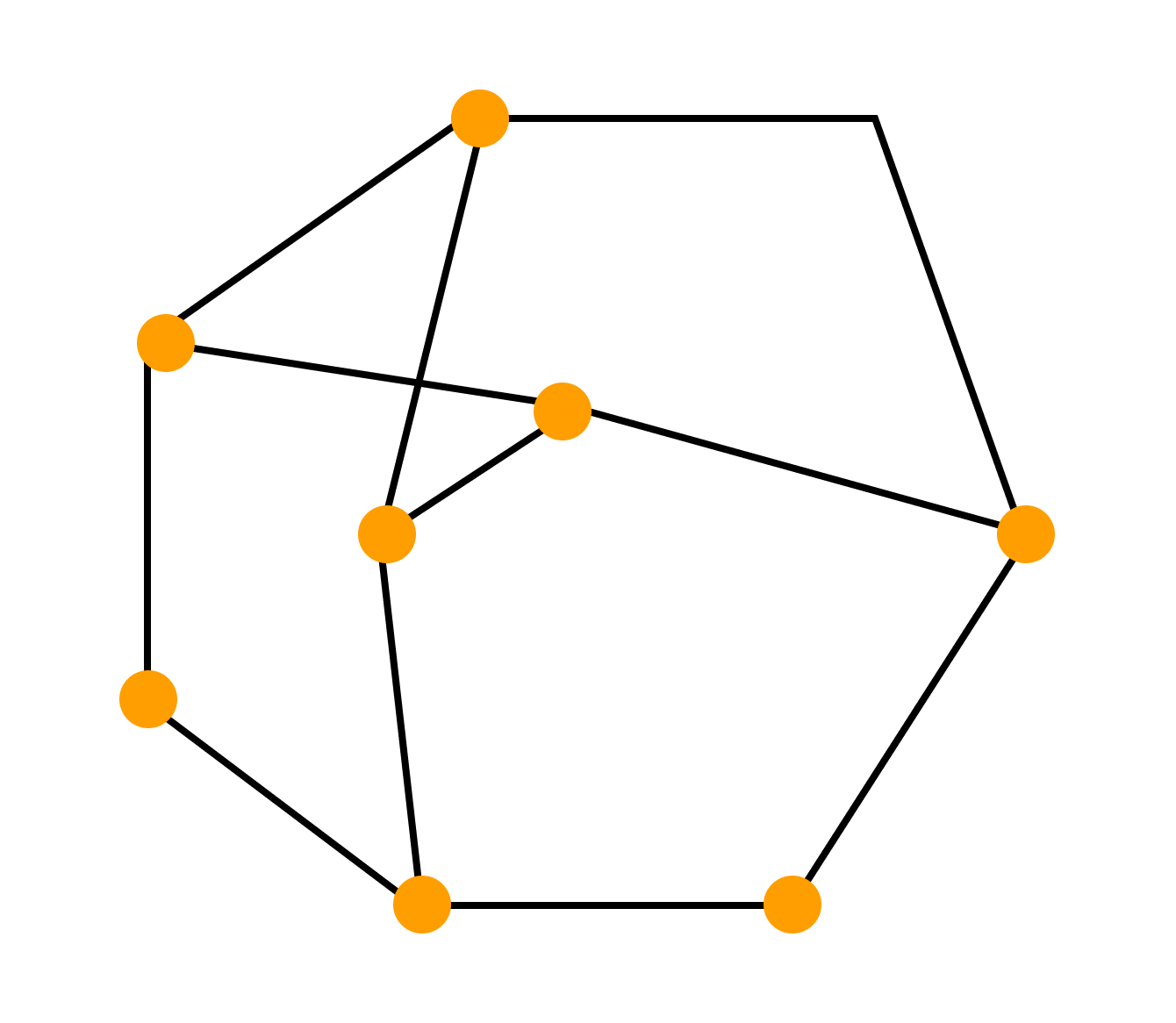
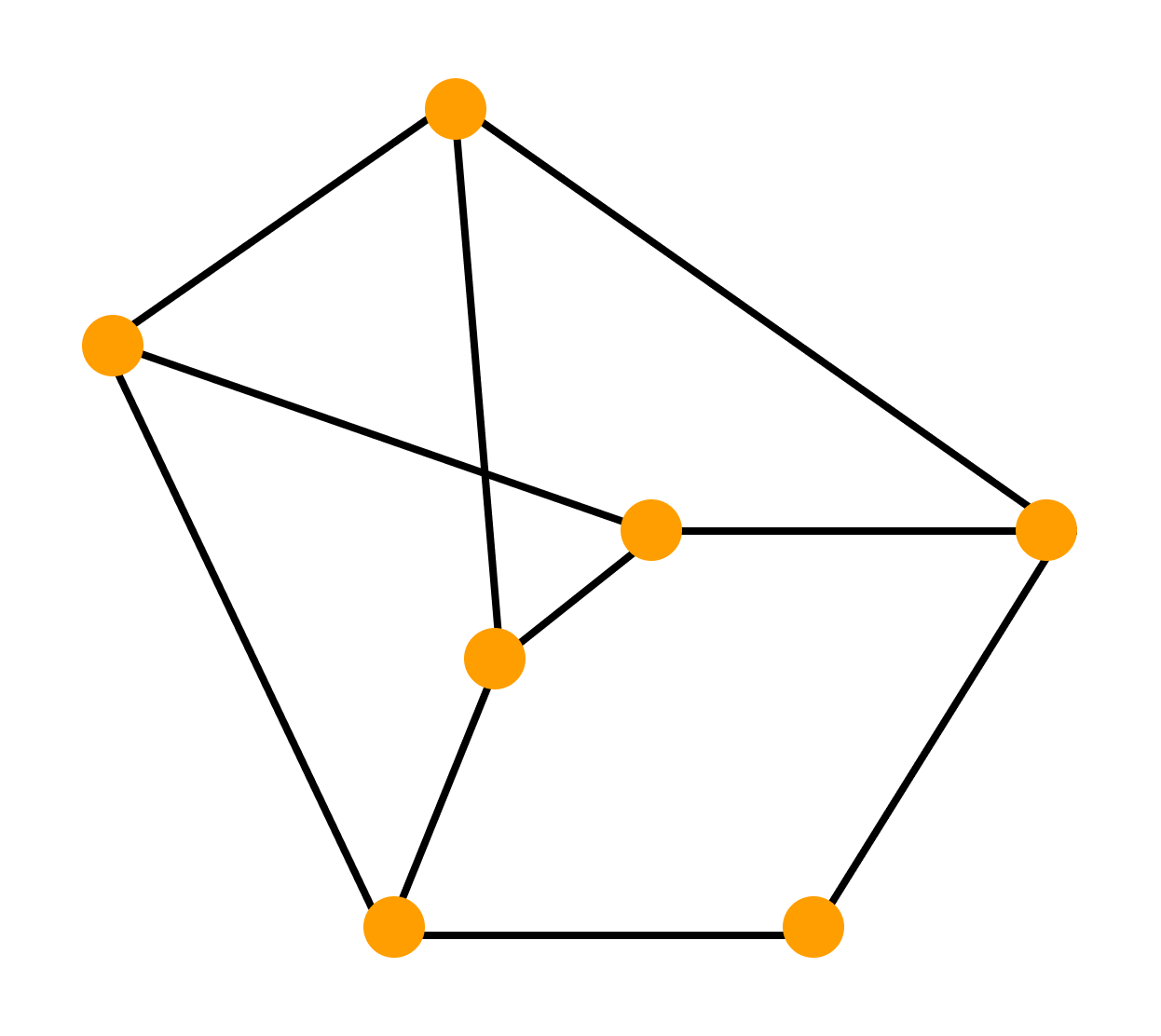
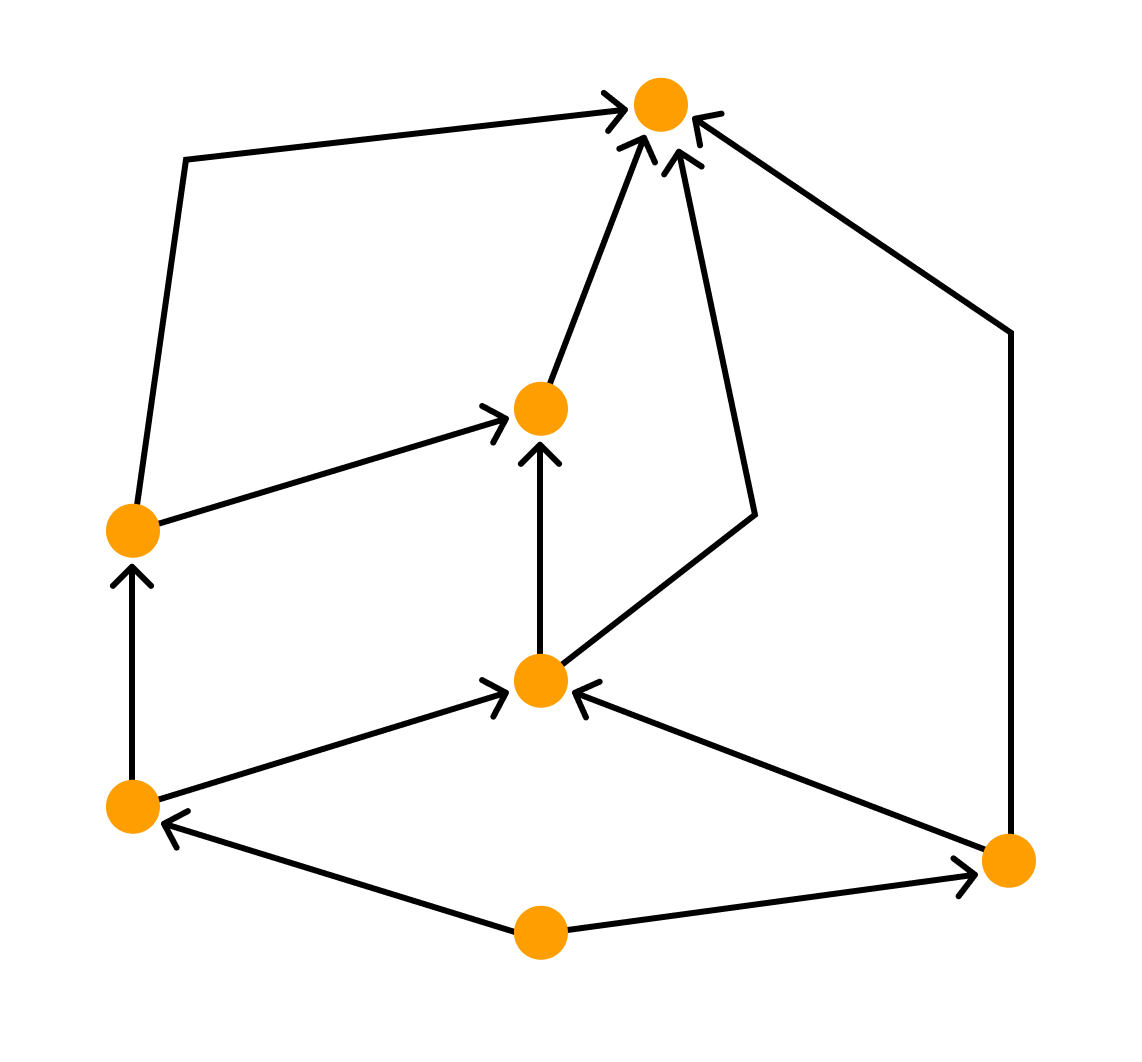
• полилинейное изображение — каждое ребро графа рисуют в виде ломаной линии
• прямолинейное изображение — каждое ребро представляют с помощью отрезка прямой
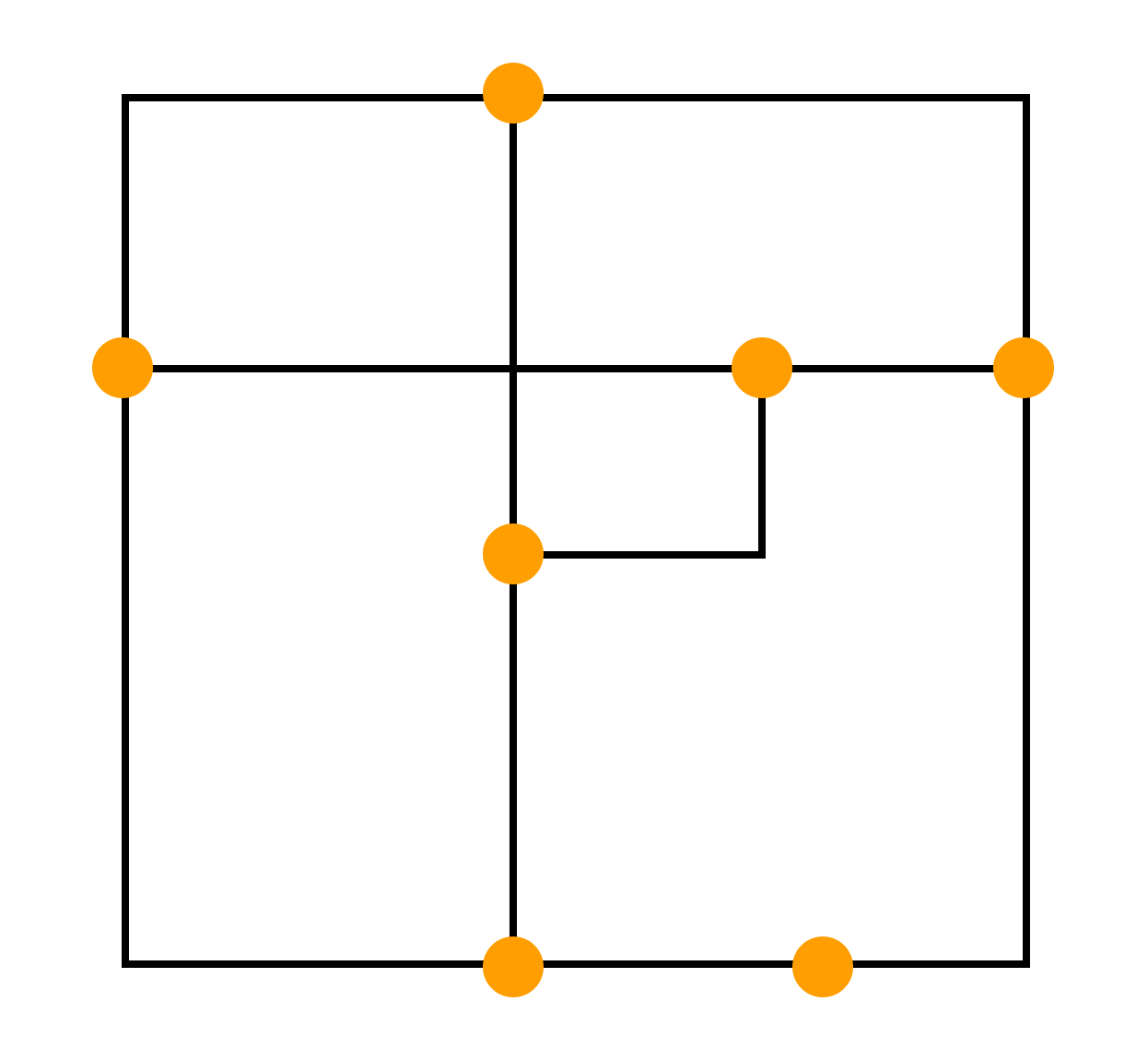
• ортогональное изображение — каждое ребро графа изображается в виде ломаной линии, состоящей из чередующихся горизонтальных и вертикальных сегментов
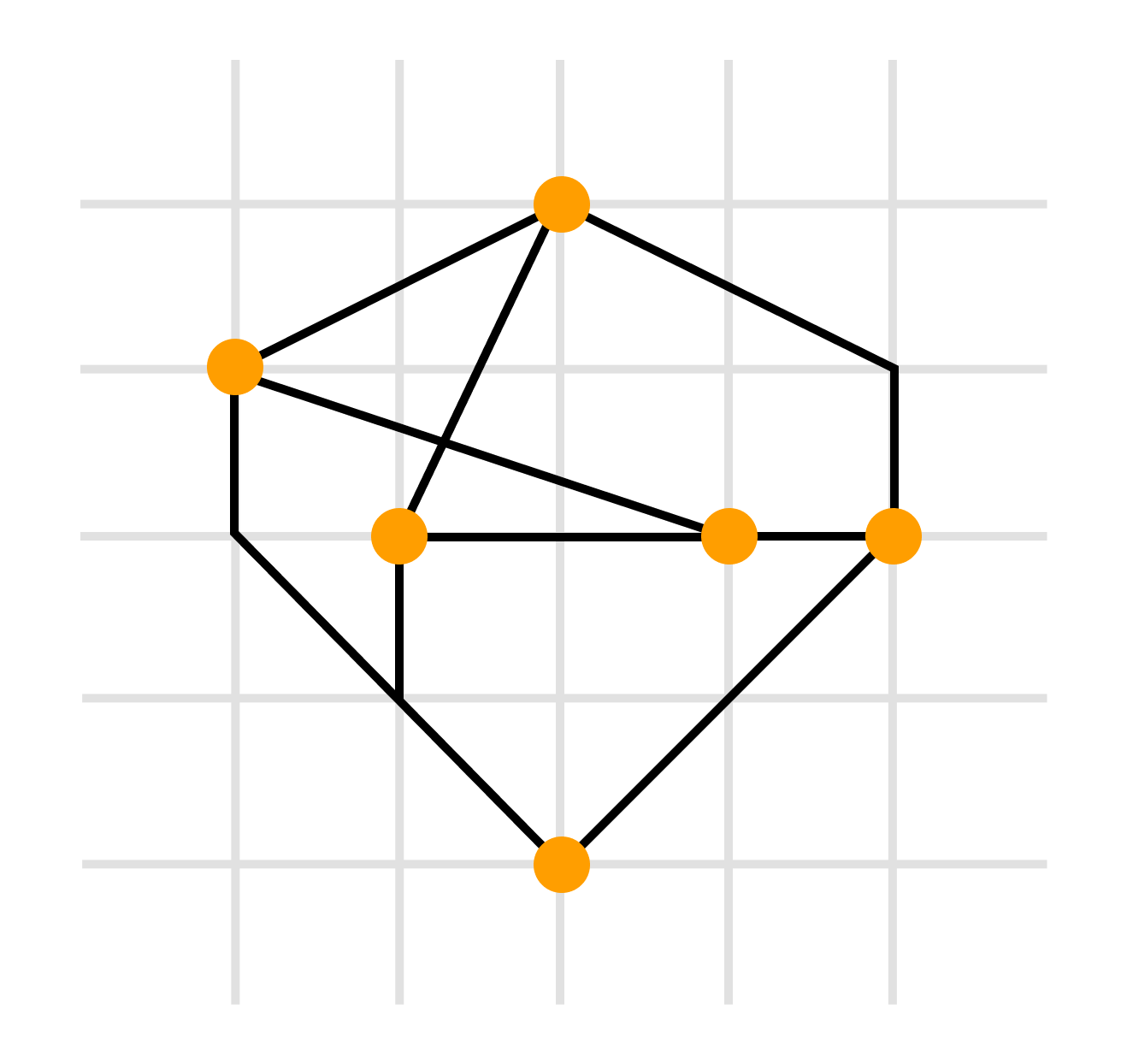
• сетчатое изображение — все вершины, а также все точки пересечения и сгибы ребер имеют целочисленные координаты. То есть находятся в узлах координатной сетки, образованной прямыми, параллельными координатным осям и пересекающими их в точках с целочисленными координатами
• плоское изображение предполагает отсутствие точек пересечения у линий, изображающих ребра.
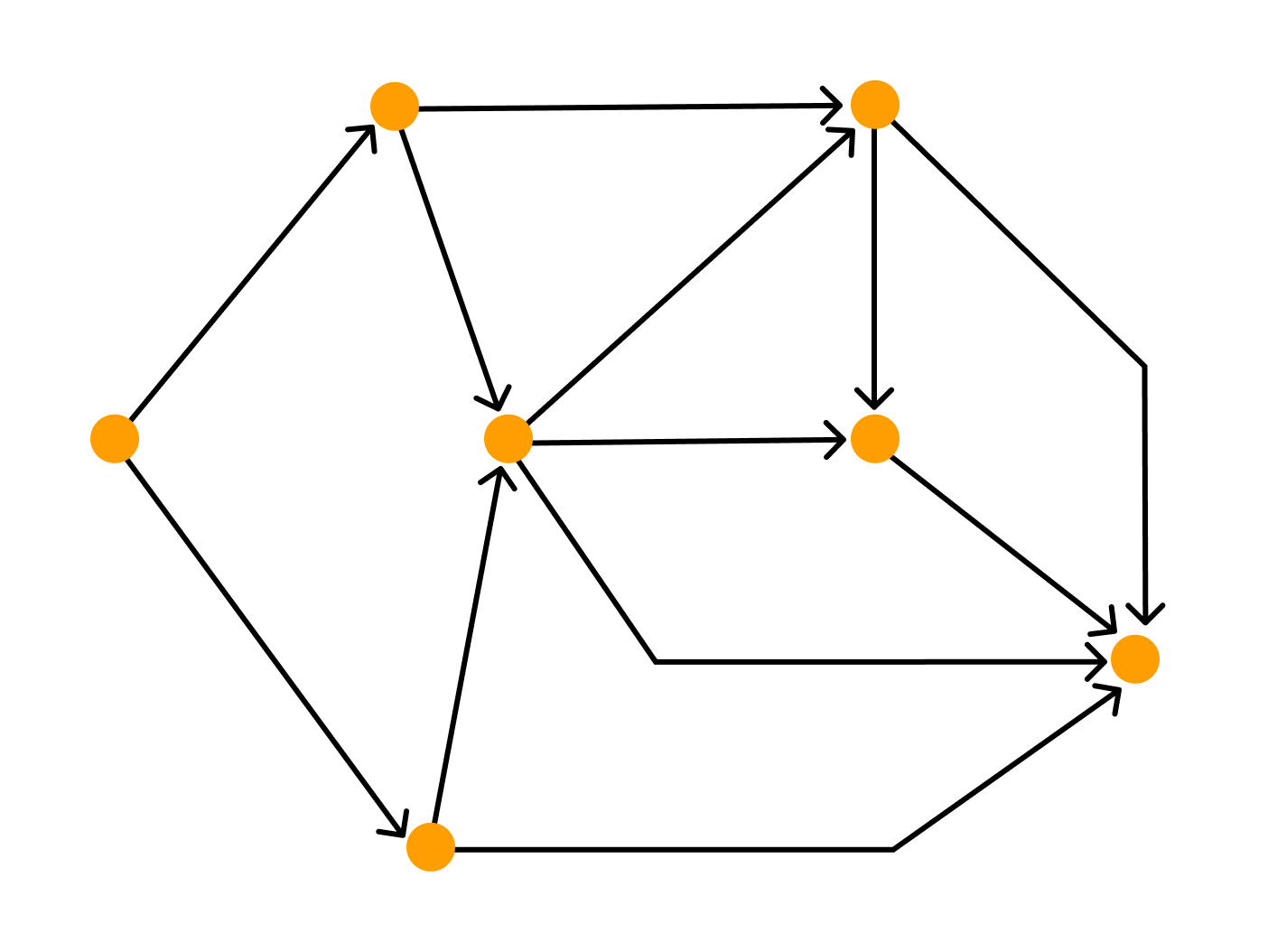
• восходящее или нисходящее изображение имеет смысл по отношению к ациклическому орграфу и предполагает, что каждая дуга изображается ориентированной линией, координаты точек которой монотонно изменяются в направлении снизу вверх или сверху вниз, а также слева направо.

Виды графов

Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.

Ориентированные и неориентированные графы

Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.



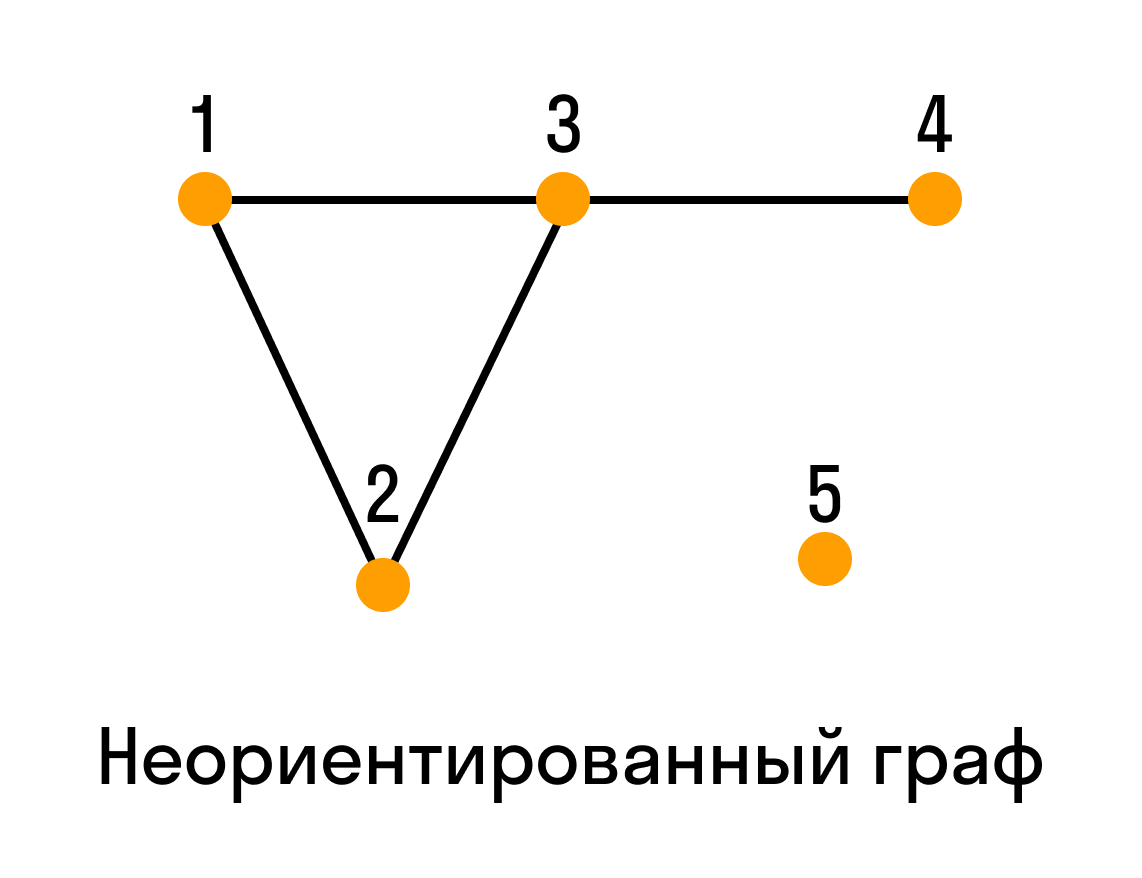
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.



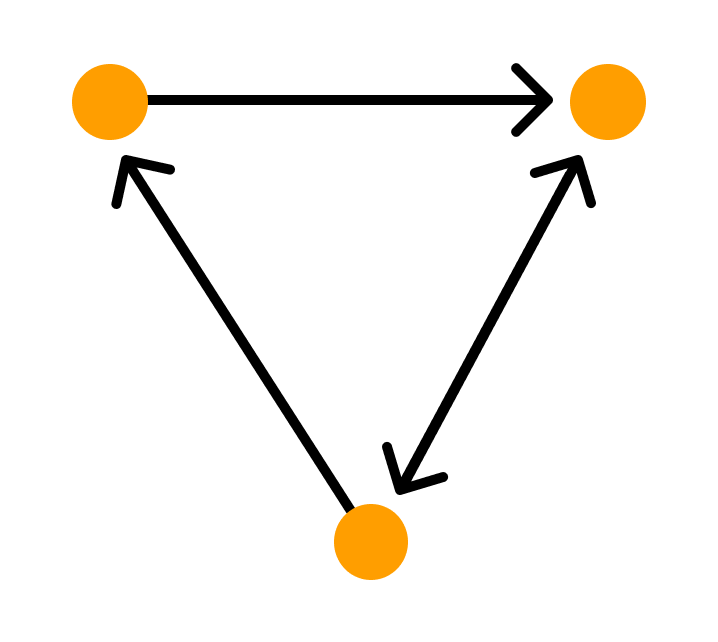
Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.

Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы

Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».

Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).



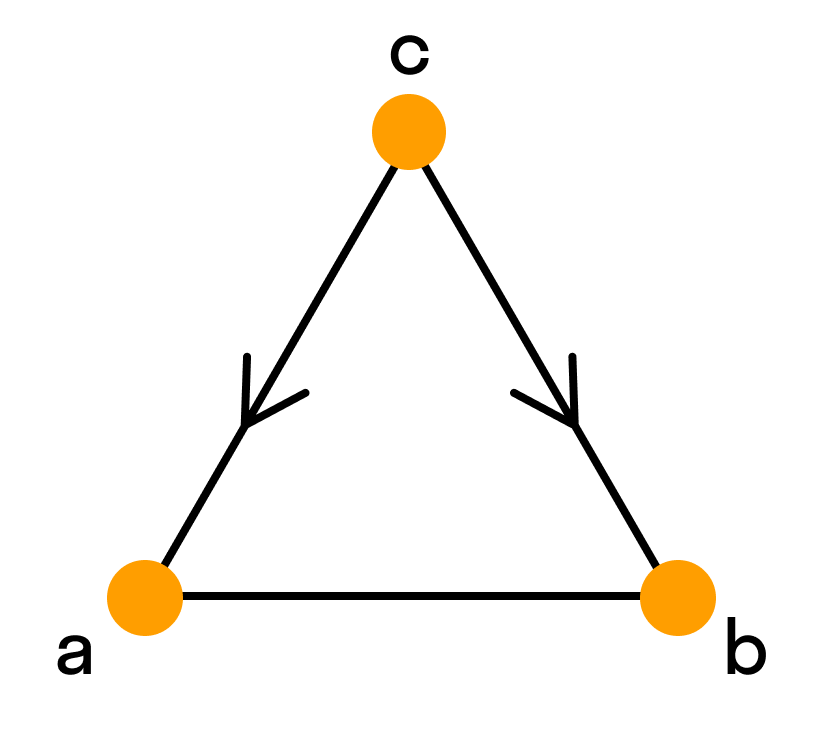
Пустой граф — это тот, что состоит только из голых вершин.



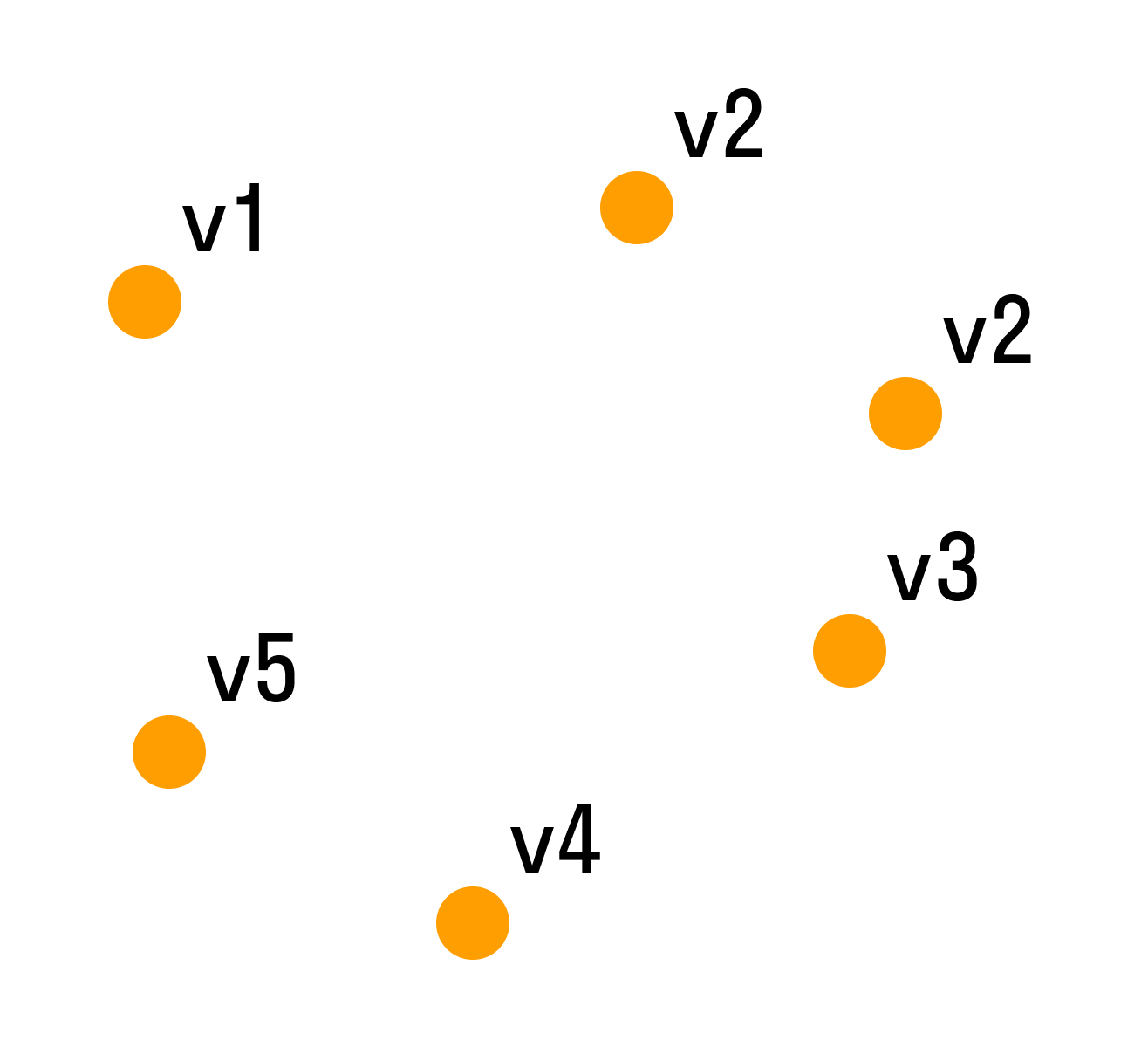
Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.



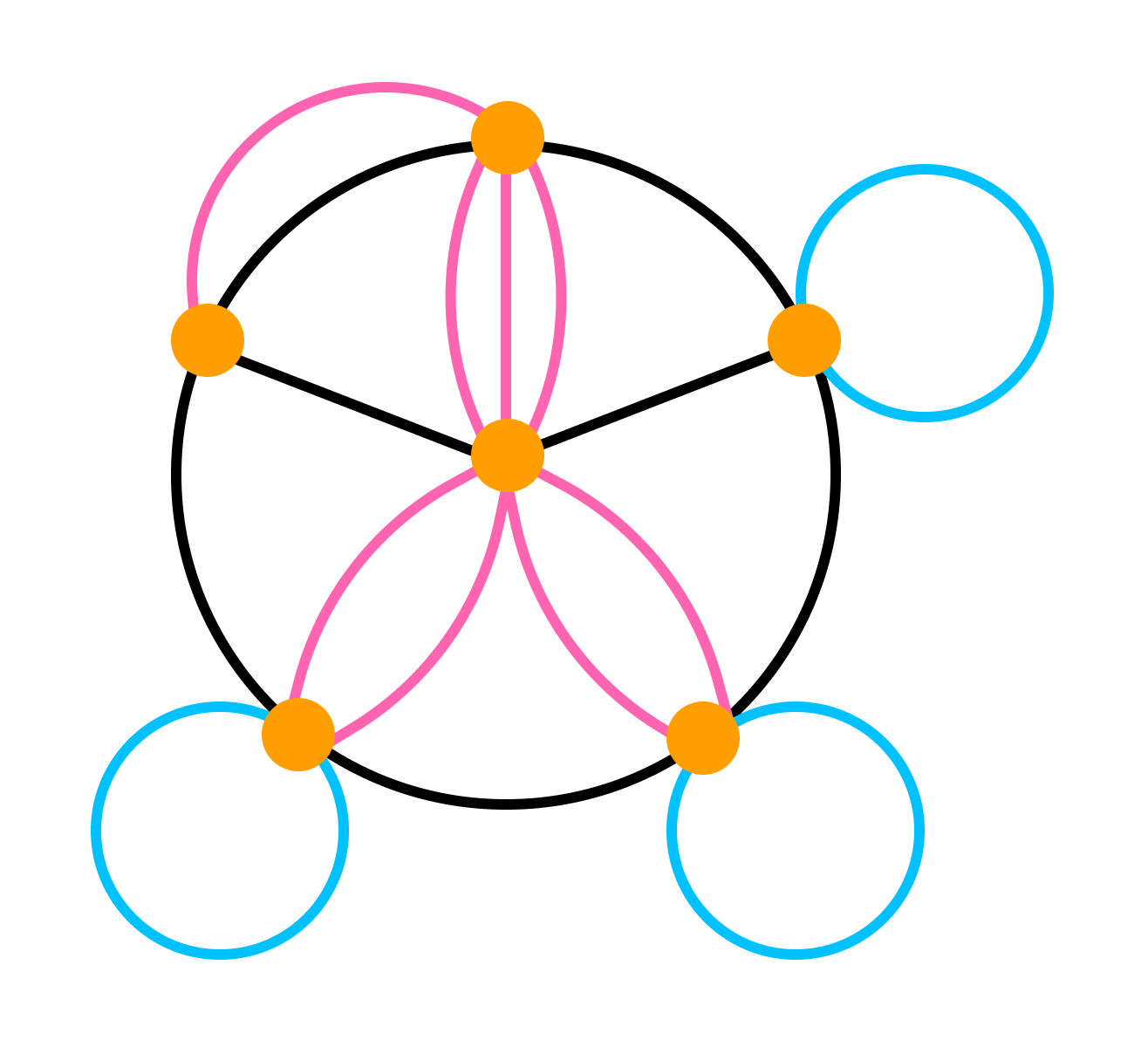
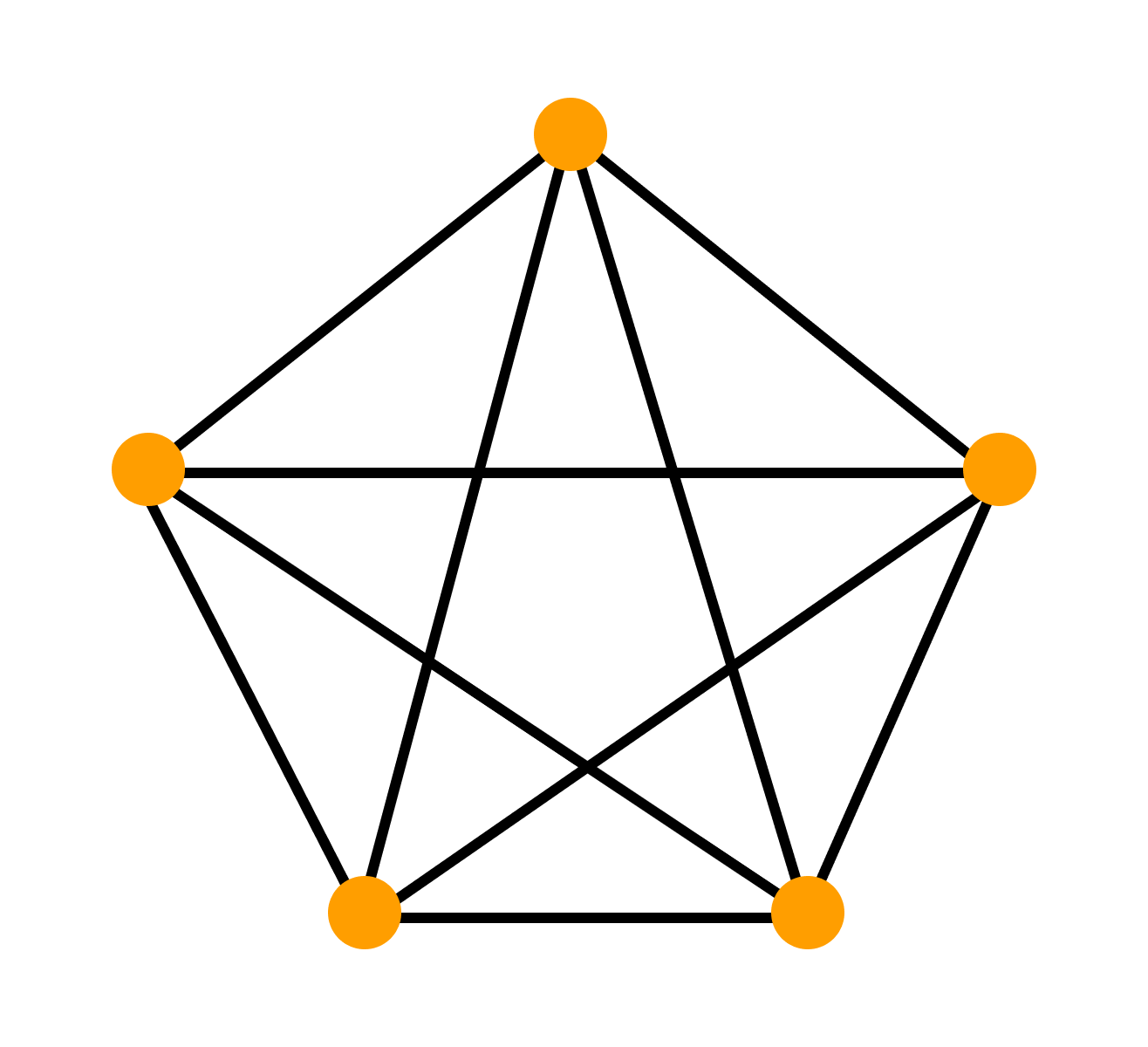
Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.



Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.



Двудольный граф

Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.



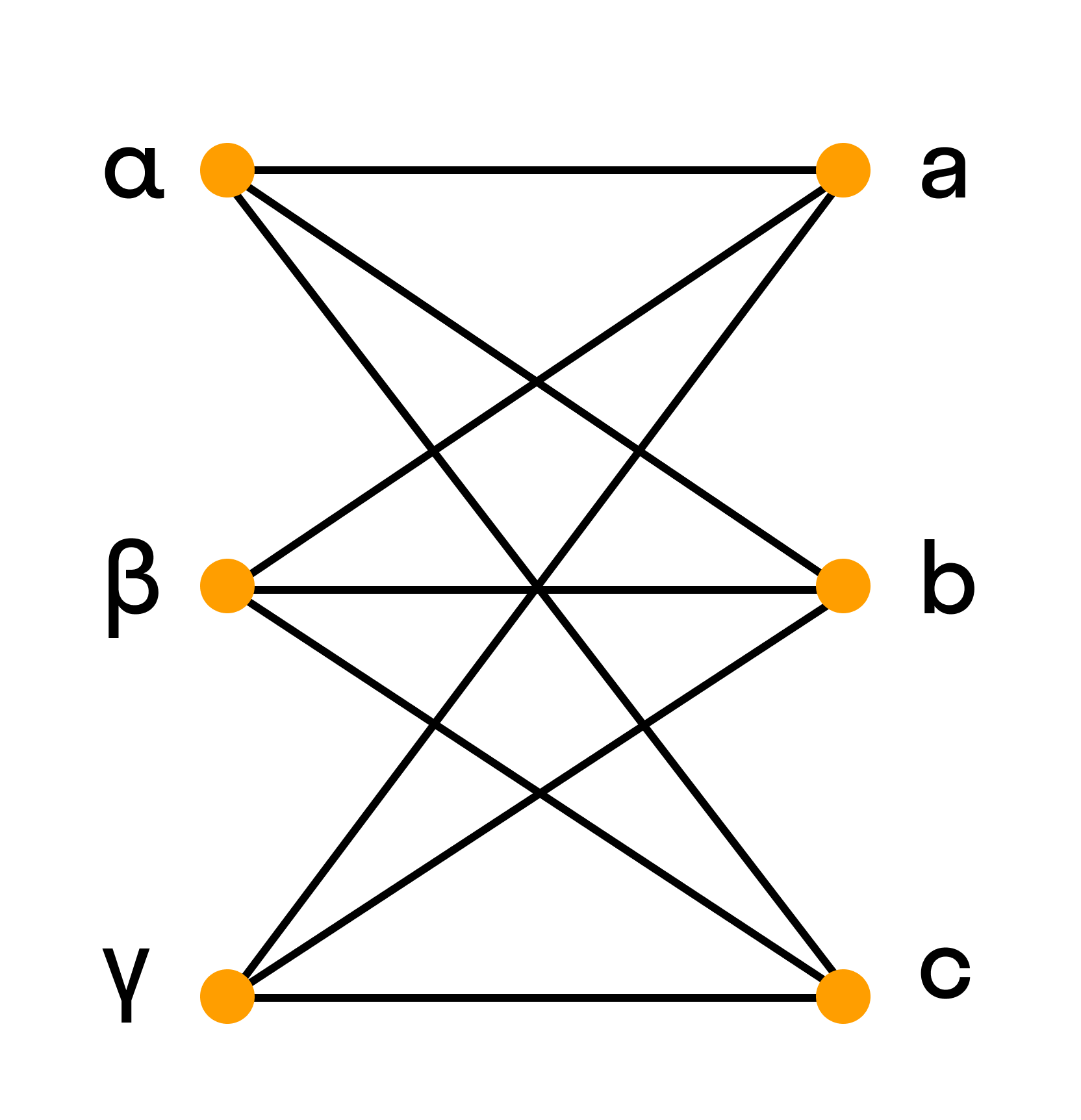
Эйлеров граф

Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.

Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?

Ответ. Если n — нечётное число, то каждая вершина инцидентна n – 1 ребрам. В таком случае наш граф — эйлеровый.



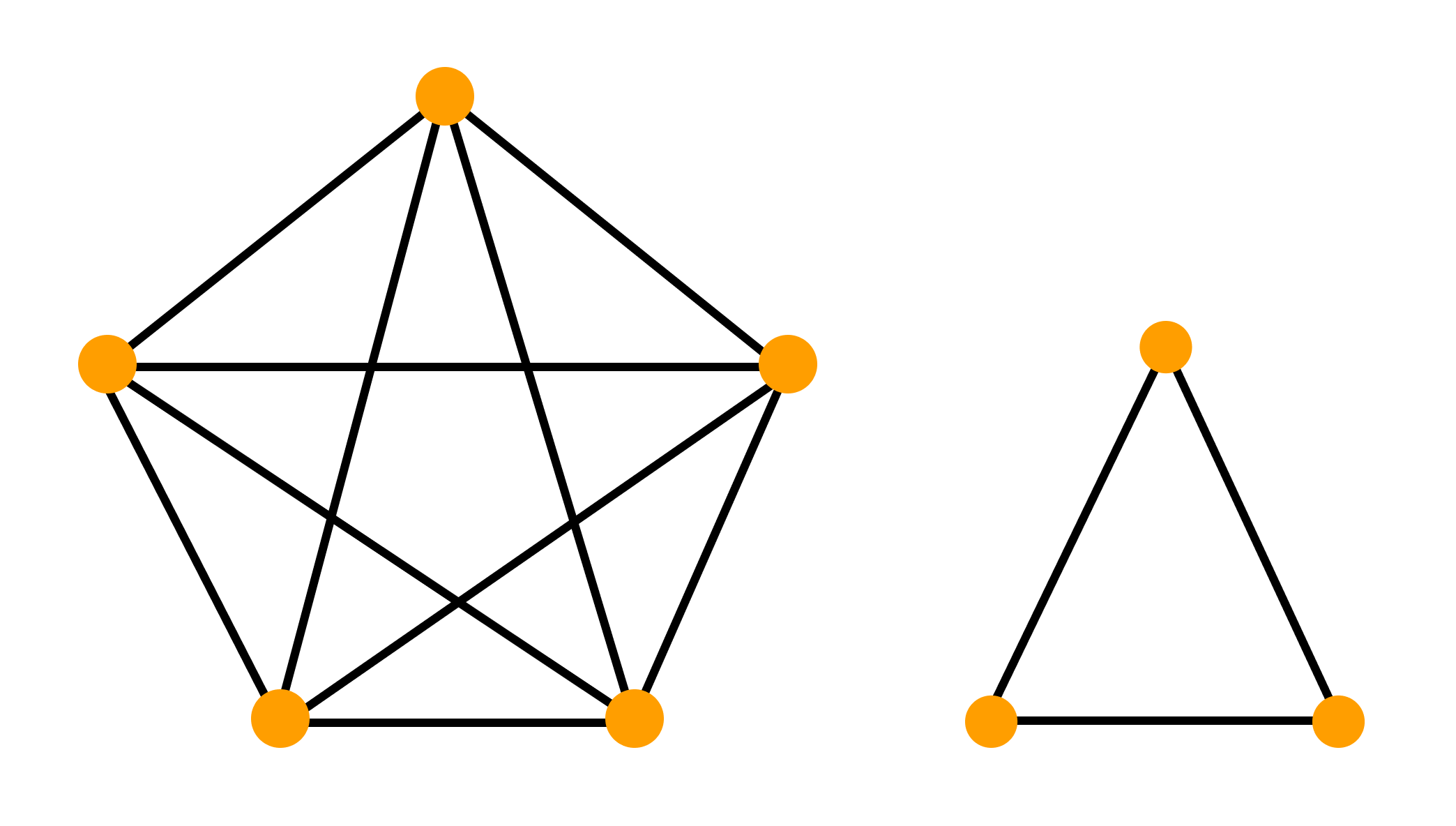
Регулярный граф

Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.

Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.

Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.

Рассуждаем так:

Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.



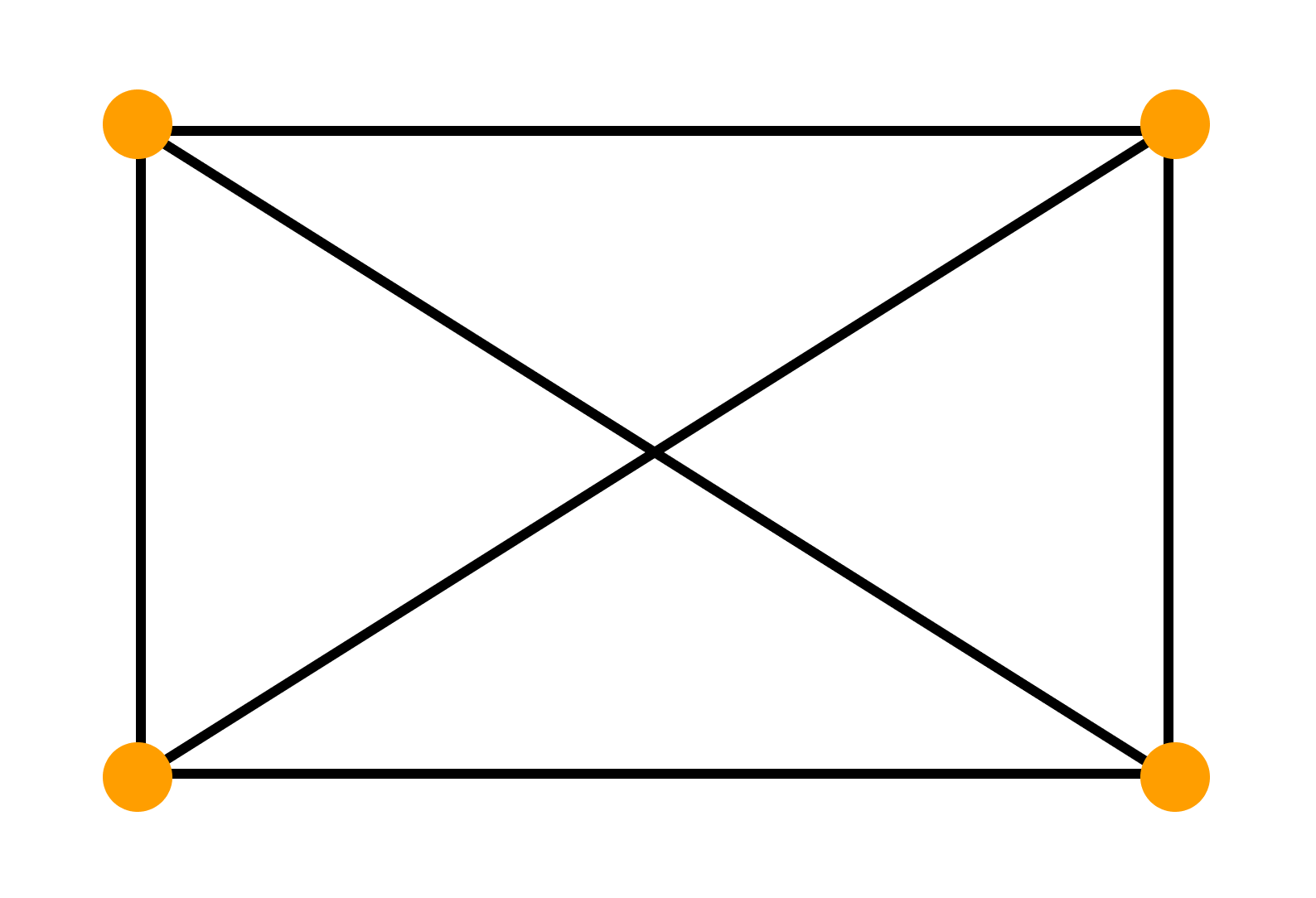
Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:



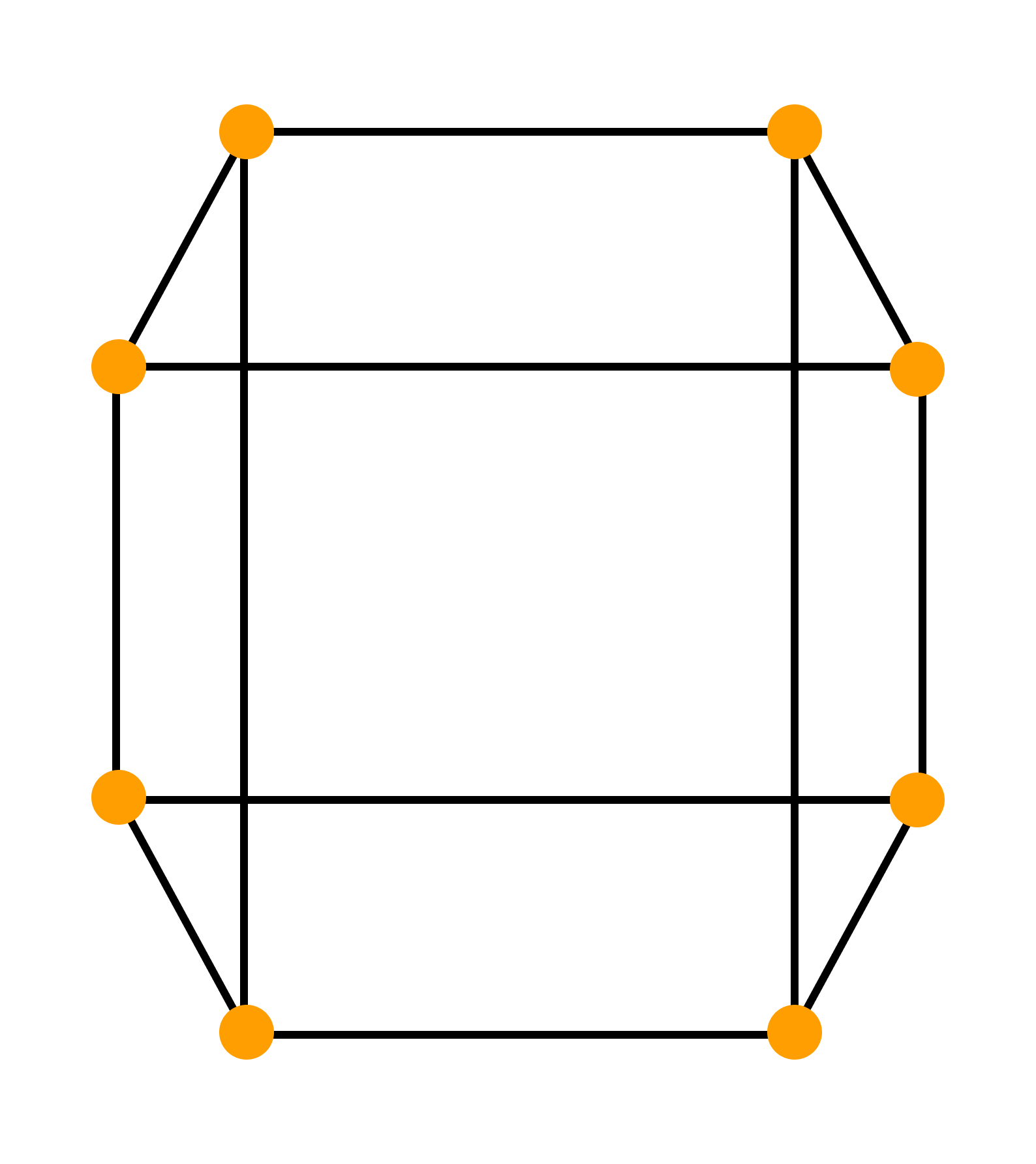
Гамильтонов граф

Гамильтоновым графом называется граф, содержащий гамильтонов цикл.

Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.

Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.



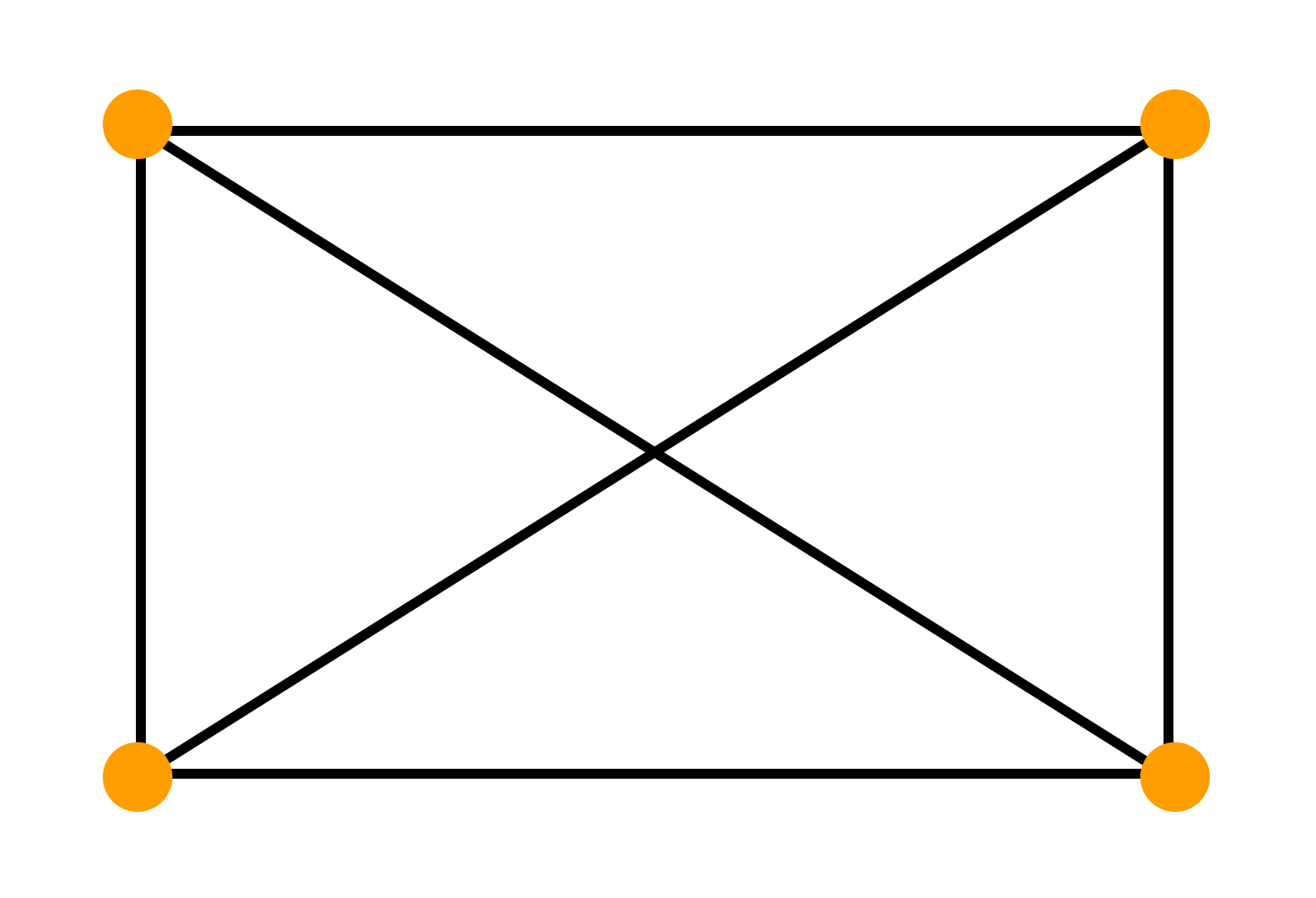
Взвешенный граф

Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.



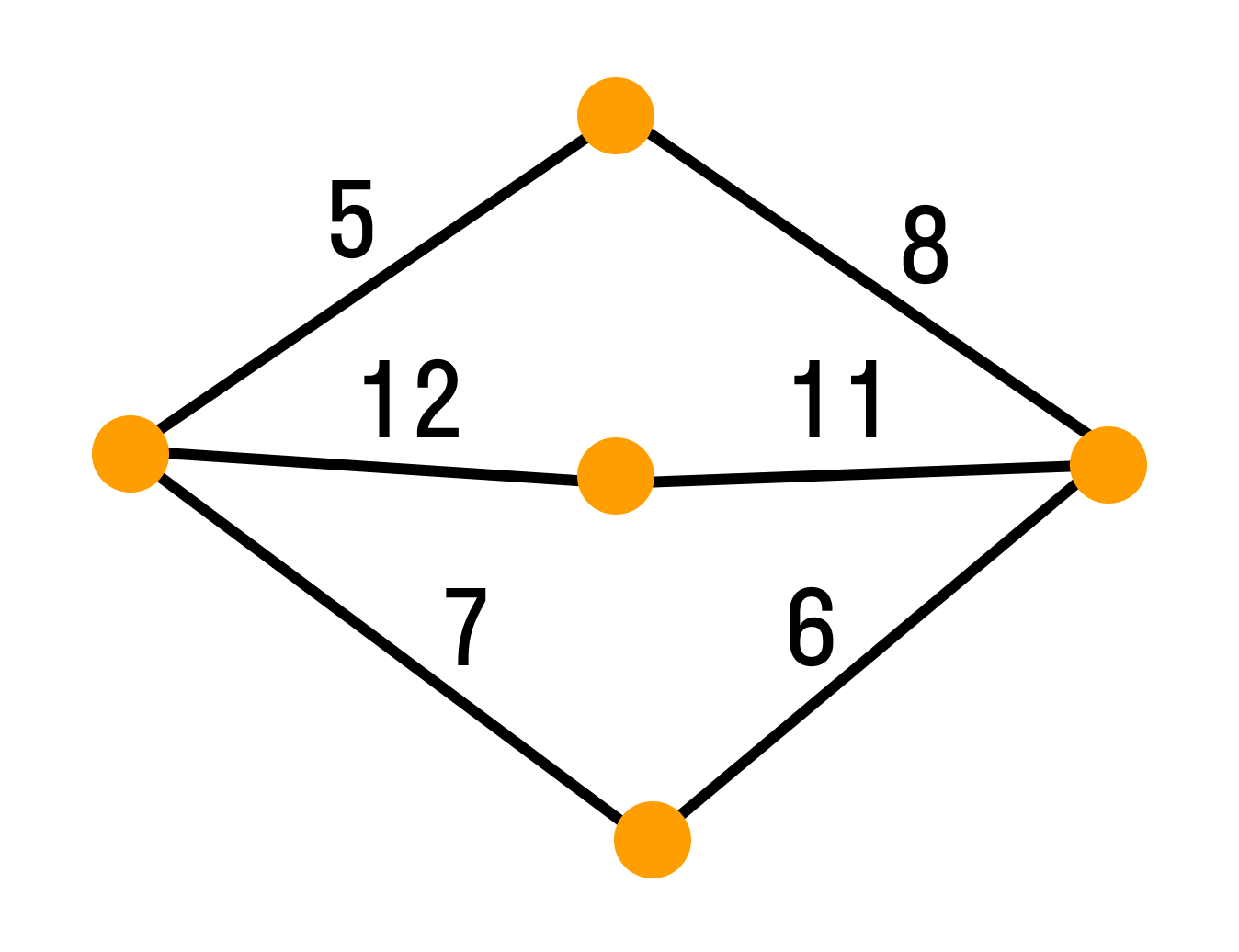
Графы-деревья

Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.



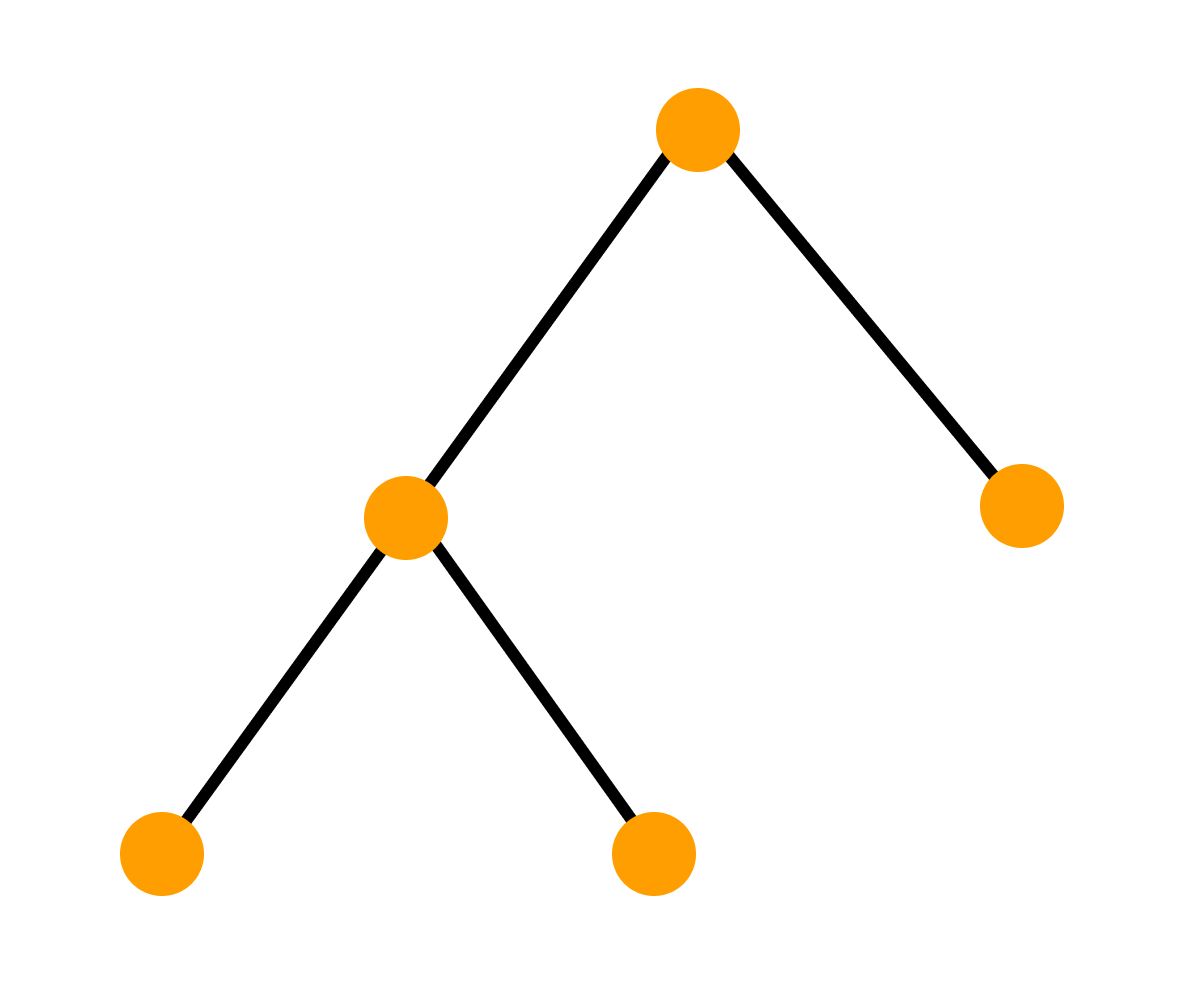
Число q ребер графа находится из соотношения q = n – 1, где n — число вершин дерева.

Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.

 

Определение дерева

Деревом называется связный граф, который не содержит циклов.

Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.

Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.

Простым путем называется путь, в котором никакое ребро не встречается дважды.

Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:

Дерево — минимальный по числу рёбер связный граф.

Висячей вершиной называется вершина, из которой выходит ровно одно ребро.

Определения дерева:

1. Деревом называется связный граф не содержащий простых циклов.
2. Деревом называется связный граф, содержащий n вершин и n – 1 ребро.
3. Деревом называется связный граф, который при удалении любого ребра перестает быть связным.
4. Деревом называется граф, в котором любые две вершины соединены ровно одним простым путем.
5.  
6.  

Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.

Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.

Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:



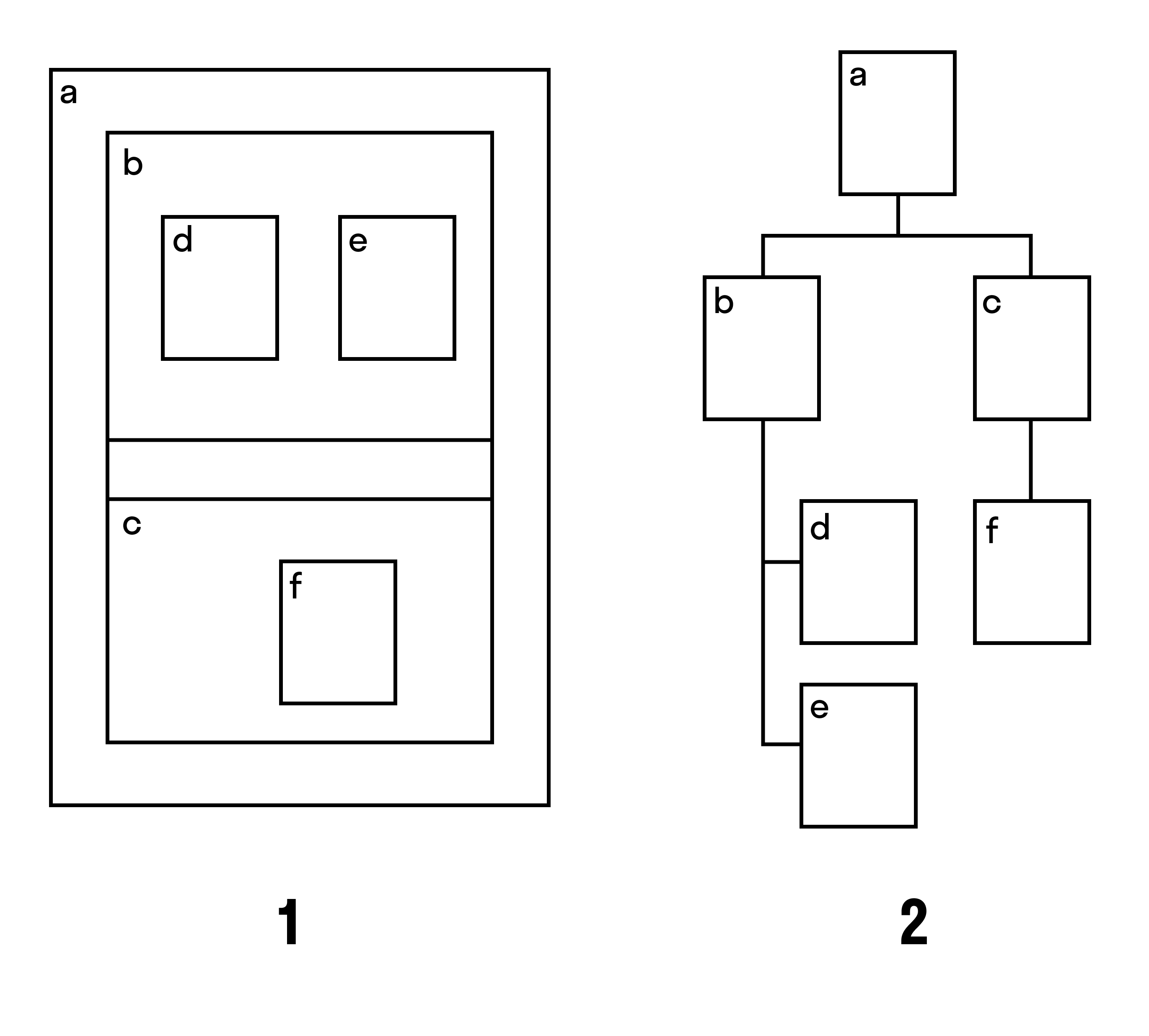
Теоремы дерева и их доказательства

I теорема

В дереве с более чем одной вершиной есть висячая вершина.

Доказательство первой теоремы:

Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.

Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.

II теорема

В дереве число вершин на 1 больше числа ребер.

Доказательство второй теоремы:

Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n < k мы доказали это факт. Найдём висячую вершину.

Граф, получающийся из исходного выкидыванием висячей вершины вместе с исходящим из нее ребром, очевидно, также является деревом — и в нём меньше на одну вершину и одно ребро. Значит для исходного графа также было верно доказываемое соотношение между количеством вершин и рёбер.

Верна и обратная теорема. Если в связном графе вершин на одну больше, чем ребер, то он является деревом.

Подграф называется остовным деревом, если он является деревом и множество его вершин совпадает с множеством вершин исходного графа.

III теорема

У любого связного графа есть остовное дерево.

Доказательство третьей теоремы:

Чтобы найти остовное дерево графа G, можно найти цикл в графе G и выкинуть одно ребро цикла — потом повторить. И так пока в графе не останется циклов. Полученный граф будет связным, так как мы выкидывали рёбра, не нарушая связность, но в нём не будет циклов. Значит, он будет деревом.

 

Теория графов и современные прикладные задачи

На основе теории графов создали разные методы решения прикладных задач, в которых в виде графов можно моделировать сложные системы. В этих моделях узлы содержат отдельные компоненты, а ребра отражают связи между компонентами.

Графы и задача о потоках

Система водопроводных труб в виде графа выглядит так:



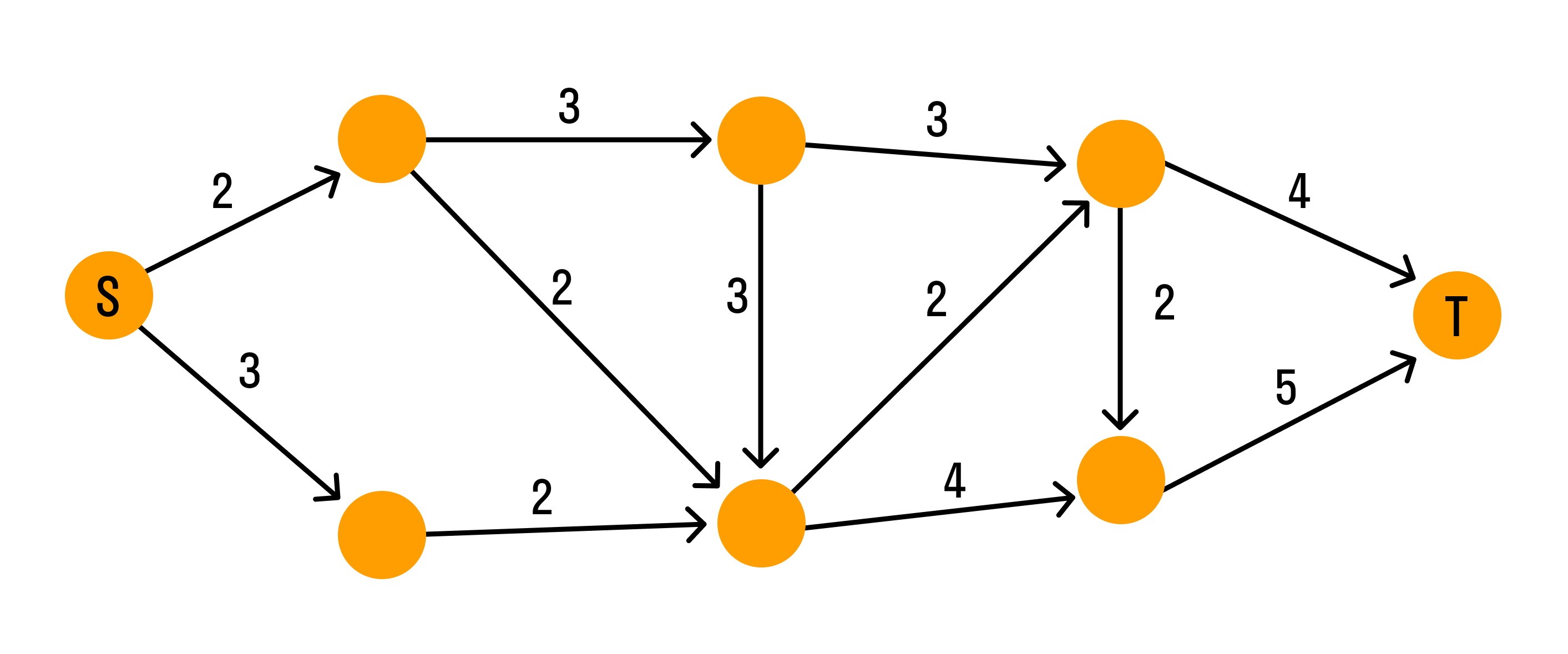
Каждая дуга графа отображает трубу. Числа над дугами (весы) — пропускная способность труб. Узлы — места соединения труб. Вода течёт по трубам только в одном направлении. Узел S — источник воды, узел T — сток.

Задача: максимизировать объём воды, протекающей от источника к стоку.

Для решения задачи о потоках можно использовать метод Форда-Фалкерсона. Идея метода в том, чтобы найти максимальный поток по шагам.

Сначала предполагают, что поток равен нулю. На каждом последующем шаге значение потока увеличивается, для чего ищут дополняющий путь, по которому поступает дополнительный поток. Эти шаги повторяют до тех пор, пока существуют дополнительные пути.

Задачу успешно применяют в различных распределенных системах: система электроснабжения, коммуникационная сеть, система железных дорог.

Графы и сетевое планирование

В задачах планирования сложных процессов, где много разных параллельных и последовательных работ, часто используют взвешенные графы. Их еще называют сетью ПЕРТ (PERT).

PERT (Program (Project) Evaluation and Review Technique) — техника оценки и анализа программ (проектов), которую используют при управлении проектами.

Сеть ПЕРТ — взвешенный ациклический ориентированный граф, в котором каждая дуга представляет работу (действие, операцию), а вес дуги — время, которое нужно на ее выполнение.

Если в сети есть дуги (a, b) и (b, c), то работа, представленная дугой (a, b), должна быть завершена до начала выполнения работы, представленной дугой (b, c). Каждая вершина (vi) представляет момент времени, к которому должны быть завершены все работы, задаваемые дугами, оканчивающимися в вершине (vi).

В таком графе:

• одна вершина, у которой нет предшественников, определяет время начала работы
• одна вершина без последователей соответствует моменту завершения комплекса работ.

Путь максимальной длины между этими вершинами графа называется критическим путем. Чтобы выполнить всю работу быстрее, нужно найти задачи на критическом пути и придумать, как их выполнить быстрее. Например, нанять больше людей, перепридумать процесс или ввести новые технологии.

From Wikipedia, the free encyclopedia

In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another.

From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects.

The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex w is said to be adjacent to another vertex v if the graph contains an edge (v,w). The neighborhood of a vertex v is an induced subgraph of the graph, formed by all vertices adjacent to v.

Types of vertices[edit]

The degree of a vertex, denoted 𝛿(v) in a graph is the number of edges incident to it. An isolated vertex is a vertex with degree zero; that is, a vertex that is not an endpoint of any edge (the example image illustrates one isolated vertex).^[1] A leaf vertex (also pendant vertex) is a vertex with degree one. In a directed graph, one can distinguish the outdegree (number of outgoing edges), denoted 𝛿 ⁺(v), from the indegree (number of incoming edges), denoted 𝛿⁻(v); a source vertex is a vertex with indegree zero, while a sink vertex is a vertex with outdegree zero. A simplicial vertex is one whose neighbors form a clique: every two neighbors are adjacent. A universal vertex is a vertex that is adjacent to every other vertex in the graph.

A cut vertex is a vertex the removal of which would disconnect the remaining graph; a vertex separator is a collection of vertices the removal of which would disconnect the remaining graph into small pieces. A k-vertex-connected graph is a graph in which removing fewer than k vertices always leaves the remaining graph connected. An independent set is a set of vertices no two of which are adjacent, and a vertex cover is a set of vertices that includes at least one endpoint of each edge in the graph. The vertex space of a graph is a vector space having a set of basis vectors corresponding with the graph’s vertices.

A graph is vertex-transitive if it has symmetries that map any vertex to any other vertex. In the context of graph enumeration and graph isomorphism it is important to distinguish between labeled vertices and unlabeled vertices. A labeled vertex is a vertex that is associated with extra information that enables it to be distinguished from other labeled vertices; two graphs can be considered isomorphic only if the correspondence between their vertices pairs up vertices with equal labels. An unlabeled vertex is one that can be substituted for any other vertex based only on its adjacencies in the graph and not based on any additional information.

Vertices in graphs are analogous to, but not the same as, vertices of polyhedra: the skeleton of a polyhedron forms a graph, the vertices of which are the vertices of the polyhedron, but polyhedron vertices have additional structure (their geometric location) that is not assumed to be present in graph theory. The vertex figure of a vertex in a polyhedron is analogous to the neighborhood of a vertex in a graph.

See also[edit]

• Node (computer science)
• Graph theory
• Glossary of graph theory

References[edit]

• Gallo, Giorgio; Pallotino, Stefano (1988). “Shortest path algorithms”. Annals of Operations Research. 13 (1): 1–79. doi:10.1007/BF02288320. S2CID 62752810.
• Berge, Claude, Théorie des graphes et ses applications. Collection Universitaire de Mathématiques, II Dunod, Paris 1958, viii+277 pp. (English edition, Wiley 1961; Methuen & Co, New York 1962; Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963; Second printing of the 1962 first English edition. Dover, New York 2001)
• Chartrand, Gary (1985). Introductory graph theory. New York: Dover. ISBN 0-486-24775-9.
• Biggs, Norman; Lloyd, E. H.; Wilson, Robin J. (1986). Graph theory, 1736-1936. Oxford [Oxfordshire]: Clarendon Press. ISBN 0-19-853916-9.
• Harary, Frank (1969). Graph theory. Reading, Mass.: Addison-Wesley Publishing. ISBN 0-201-41033-8.
• Harary, Frank; Palmer, Edgar M. (1973). Graphical enumeration. New York, Academic Press. ISBN 0-12-324245-2.

External links[edit]

• Weisstein, Eric W. “Graph Vertex”. MathWorld.

Зачем вообще изучать графовые алгоритмы?

Графовые алгоритмы представляют собой последовательность шагов для обхода графа через вершины (узлы). Некоторые алгоритмы используются для поиска определенного узла или пути между двумя заданными узлами.

Данные алгоритмы применяют на сайтах социальных сетей, в моделировании конечного автомата, а также во многих других сферах. Я приложил свой исходный код для всех алгоритмов, про которые мы будем говорить ниже.

1. Поиск в ширину (Breadth First Searching)

Поиск в ширину — это рекурсивный алгоритм поиска всех вершин графа или дерева. Обход начинается с корневого узла и затем алгоритм исследует все соседние узлы. Затем выбирается ближайший узел и исследуются все неисследованные узлы. При использовании BFS для обхода любой узел графа можно считать корневым узлом.

Простой алгоритм для BFS, который нужно запомнить:

1. Перейдите на соседнюю нерассмотренную вершину. Отметьте как рассмотренную. Отобразите это. Вставьте ее в очередь.
2. Если смежная вершина не найдена, удалите первую вершину из очереди.
3. Повторяйте шаг 1 и шаг 2, пока очередь не станет пустой.

Схематическое представление обхода BFS:

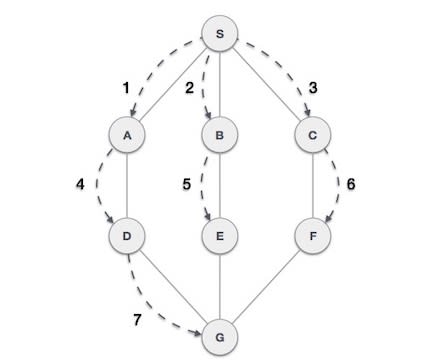
Ссылка на код: Поиск в ширину

2. Поиск в глубину (Depth First Searching)

Поиск в глубину или обход в глубину — это рекурсивный алгоритм поиска всех вершин графа или древовидной структуры данных.

Алгоритм поиска в глубину (DFS) осуществляет поиск вглубь графа, а также использует стек, чтобы не забыть «получить» следующую вершину для начала поиска, когда на любой итерации возникает тупик.

Простой алгоритм, который нужно запомнить, для DFS:

1. Посетите соседнюю непосещенную вершину. Отметьте как посещенную. Отобразите это. Добавьте в стек.
2. Если смежная вершина не найдена, то вершина берется из стека. Стек выведет все вершины, у которых нет смежных вершин.
3. Повторяйте шаги 1 и 2, пока стек не станет пустым.

Схематическое представление обхода DFS:

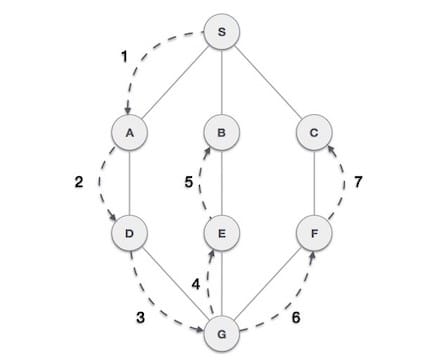
Ссылка на код: Поиск в глубину

Если хочешь подтянуть свои знания по алгоритмам, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:

• углубишься в теорию структур данных;
• научишься решать сложные алгоритмические задачи;
• научишься применять алгоритмы и структуры данных при разработке программ.

3. Топологическая сортировка (Topological Sorting)

Топологическая сортировка для ориентированного ациклического графа (DAG) — это линейное упорядочивание вершин, при котором вершина u предшествует v для каждого направленного ребра uv (в порядке очереди). Топологическая сортировка для графа невозможна, если граф не является DAG.

Для одного графа может применяться более одной топологической сортировки.

Простой алгоритм, который следует запомнить, для топологической сортировки:

1. Отметьте u как посещенную

2. Для всех вершин v, смежных с u, выполните:

2.1. Если v не посещенная, то:

2.2. Выполняем TopoSort (не забывая про стек)

2.3. Цикл выполнен

3. Запишите u в стек

Схематическое представление топологической сортировки:

Пример топологической сортировки для этого графа:

5 → 4 → 2 → 3 → 1 → 0

Ссылка на код: Топологическая сортировка

4. Обнаружение цикла с помощью алгоритма Кана (Kahn’s Algorithm)

Алгоритм топологической сортировки Кана — это алгоритм обнаружения циклов на базе эффективной топологической сортировки.

Работа алгоритма осуществляется путем нахождения вершины без входящих в нее ребер и удаления всех исходящих ребер из этой вершины.

Ссылка на код: Обнаружение цикла с использованием алгоритма Кана

5. Алгоритм Дейкстры (Dijkstra’s Algorithm)

Алгоритм Дейкстры позволяет найти кратчайший путь между любыми двумя вершинами графа. Он отличается от минимального остовного дерева тем, что кратчайшее расстояние между двумя вершинами может не включать все вершины графа.

Ниже проиллюстрирован алгоритм кратчайшего пути с одним источником. Здесь наличие одного источника означает, что мы должны найти кратчайший путь от источника ко всем узлам.

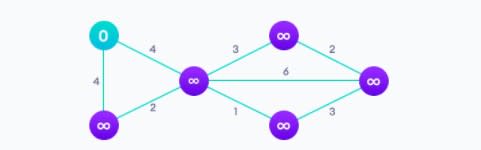
После применения алгоритма Дейкстры:

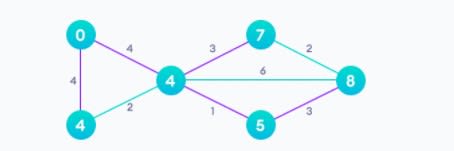
Ссылка на код: Алгоритм Дейкстры

6. Алгоритм Беллмана-Форда (Bellman Ford’s Algorithm)

Алгоритм Беллмана-Форда помогает нам найти кратчайший путь от вершины ко всем другим вершинам взвешенного графа. Он похож на алгоритм Дейкстры, но может обнаруживать графы, в которых ребра могут иметь циклы с отрицательным весом.

Алгоритм Дейкстры (не обнаруживает цикл с отрицательным весом) может дать неверный результат, потому что проход через цикл с отрицательным весом приведет к уменьшению длины пути. Дейкстра не применим для графиков с отрицательными весами, а Беллман-Форд, наоборот, применим для таких графиков. Беллман-Форд также проще, чем Дейкстра и хорошо подходит для систем с распределенными параметрами.

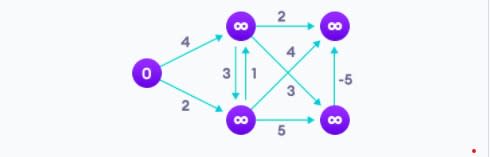
Результат алгоритма Беллмана-Форда:

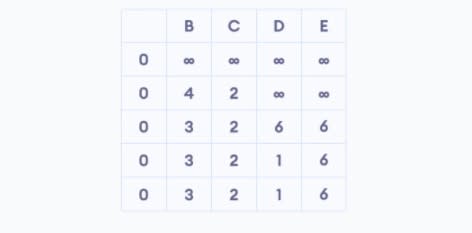
Ссылка на код: Алгоритм Беллмана Форда

7. Алгоритм Флойда-Уоршалла (Floyd-Warshall Algorithm)

Алгоритм Флойда-Уоршалла — это алгоритм поиска кратчайшего пути между всеми парами вершин во взвешенном графе. Этот алгоритм работает как для ориентированных, так и для неориентированных взвешенных графов. Но это не работает для графов с отрицательными циклами (где сумма ребер в цикле отрицательна). Здесь будет использоваться концепция динамического программирования.

Алгоритм, лежащий в основе алгоритма Флойда-Уоршалла:

D_ij(k) ← min ( D_ij(k-1), D_ij(k-1)+D_kj(k-1))

Ссылка на код: Алгоритм Флойда-Уоршалла

8. Алгоритм Прима (Prim’s Algorithm)

Алгоритм Прима — это жадный алгоритм, который используется для поиска минимального остовного дерева из графа. Алгоритм Прима находит подмножество ребер, которое включает каждую вершину графа, так что сумма весов ребер может быть минимизирована.

Простой алгоритм для алгоритма Прима, который следует запомнить:

1. Выберите минимальное остовное дерево со случайно выбранной вершиной.
2. Найдите все ребра, соединяющие дерево с новыми вершинами, найдите минимум и добавьте его в дерево.
3. Продолжайте повторять шаг 2, пока мы не получим минимальное остовное дерево.

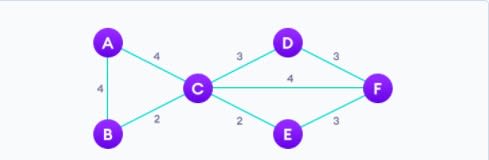
Получим:

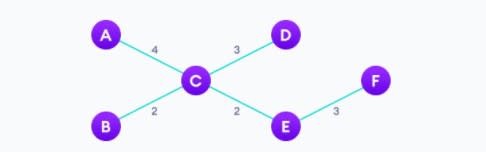
Ссылка на код: Алгоритм Прима

9. Алгоритм Краскала (Kruskal’s Algorithm)

Алгоритм Краскала используется для нахождения минимального остовного дерева для связного взвешенного графа. Основная цель алгоритма — найти подмножество ребер, с помощью которых мы можем обойти каждую вершину графа. Он является жадным алгоритмом, т. к. находит оптимальное решение на каждом этапе вместо поиска глобального оптимума.

Простой алгоритм Краскала, который следует запомнить:

1. Сначала отсортируйте все ребра по весу (от наименьшего к наибольшему).
2. Теперь возьмите ребро с наименьшим весом и добавьте его в остовное дерево. Если добавляемое ребро создает цикл, не берите такое ребро.
3. Продолжайте добавлять ребра, пока не достигнете всех вершин и не будет создано минимальное остовное дерево.

Ссылка на код: Алгоритм Краскала

10. Алгоритм Косараджу (Kosaraju’s Algorithm)

Если мы можем достичь каждой вершины компонента из любой другой вершины этого компонента, то он называется сильно связанным компонентом (SCC). Одиночный узел всегда является SCC. Алгоритм Флойда-Уоршалла относится к методам полного перебора. Но для получения наилучшей временной сложности мы можем использовать алгоритм Косараджу.

Простой алгоритм Косараджу, который следует запомнить:

1. Выполните обход графа DFS. Поместите узел в стек перед возвратом.
2. Найдите граф транспонирования, поменяв местами ребра.
3. Извлекайте узлы один за другим из стека и снова в DFS на модифицированном графе.

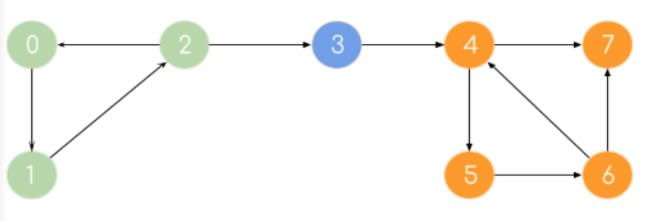
Получим:

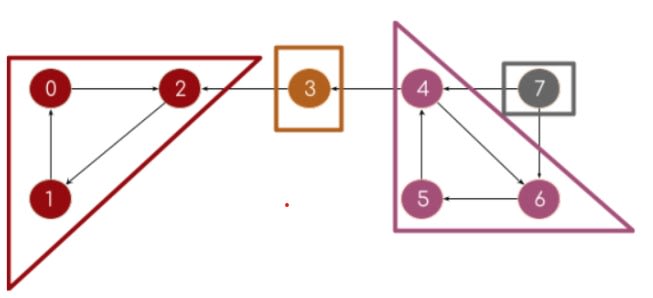
Ссылка на код: Алгоритм Косараджу

В этой статье мы познакомились с самыми важными алгоритмами, которые должен знать каждый программист, работающий с графами. Если хотите подтянуть или освежить знания по алгоритмам и структурам данных, загляни на наш курс «Алгоритмы и структуры данных», который включает в себя:

• живые вебинары 2 раза в неделю;
• 47 видеолекций и 150 практических заданий;
• консультации с преподавателями курса.

***

Материалы по теме

• 🌳 Деревья и графы: что это такое и почему их обязательно нужно знать каждому программисту
• ❓ Зачем разработчику знать алгоритмы и структуры данных?
• ❓ Пройди тест на знание алгоритмов и структур данных