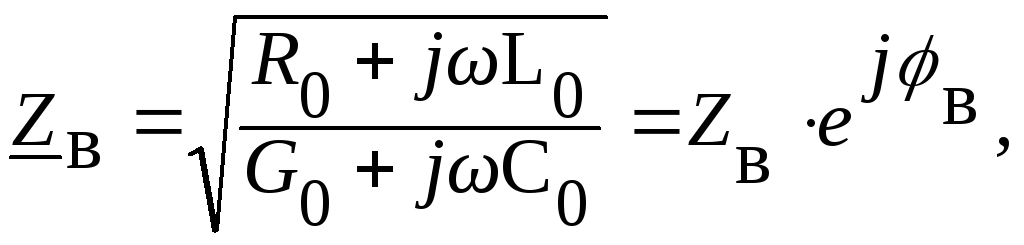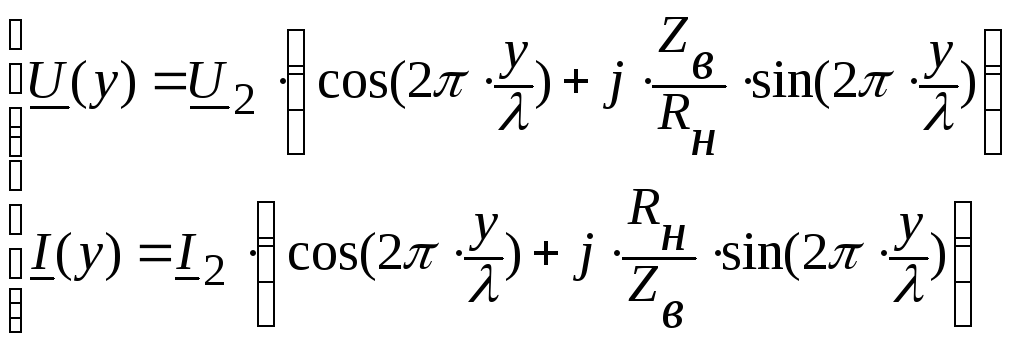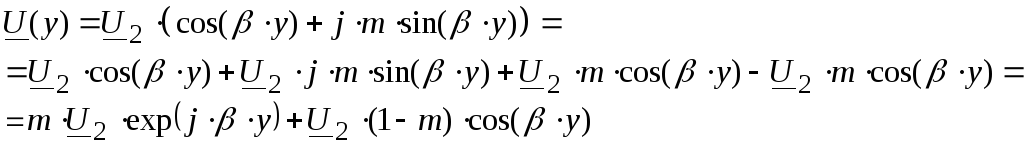Входное сопротивление как его найти

Входное и выходное сопротивление является очень важным в электронике.

Предисловие

Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:

состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.

В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:

Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.

Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.

— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?

Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.

На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.

Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.

Входное сопротивление

Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.

Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение U_вхот другого блока или от источника питания, а на его выходе появится напряжение U_вых(или не появится, если блок является конечным).

Но раз уж мы подаем напряжение на вход (входное напряжение U_вх), следовательно, у нас этот блок будет кушать какую-то силу тока I_вх.

Теперь самое интересное… От чего зависит I_вх? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.

То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.

Как измерить входное сопротивление

Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?

1)Замерить напряжение U_вх, подаваемое на этот блок

2)Замерить силу тока I_вх, которую потребляет наш блок

3) По закону Ома найти входное сопротивление R_вх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.

Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).

Падение напряжения на резисторе R обозначим, как U_R

Из всего этого получаем…

Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!

Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление R_вх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.

В результате получается цепь:

Высчитываем силу тока в цепи в Амперах

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.

Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.

Измерение входного сопротивления на практике

Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:

А на деле вот так:

Итак, у нас получилось 22,5 миллиАмпер.

Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:

Получаем:

Выходное сопротивление

Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.

Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:

И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.

Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.

У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).

Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.

В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (E_{эквивалентное}) и с каким-то внутренним сопротивлением (R_{эквивалентное}).

E_экв— эквивалентный источник ЭДС

R_экв— эквивалентное сопротивление

То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.

В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить R_вых?

В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания I_кз.

В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.

Измерение выходного сопротивления на практике

Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.

Итак, для начала замеряем напряжение на аккумуляторе без лампочки.

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:

Заключение

Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.

С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.

Источник

Что такое входное сопротивление и как его измерить

Содержание

1 Понятие входного сопротивления для постоянного тока
2 Что такое внутреннее сопротивление при переменном токе
3 Как измерить
4 Выходное напряжение
5 Практическое применение
6 Видео по теме

При работе со сложными схемами нужно уметь определять характеристики их отдельных блоков и элементов. В частности, входное и выходное сопротивление. Важно знать, что они из себя представляют, как определяются и какую роль играют в работе устройства.

Понятие входного сопротивления для постоянного тока

Радиоэлектронные устройства могут быть не только относительно, но и очень сложными, состоящими из многих блоков. Однако независимо от сложности устройства, количества используемых в нем деталей, схему можно рассматривать в качестве совокупности простых частей с определенной разностью потенциалов на входе. На выходе блока имеется ещё два контакта, на которых также присутствует напряжение. В первом случае его называют входным, в другом — выходным. Сказанное можно пояснить следующим рисунком.

Входное сопротивление цепи можно легко измерить с помощью вольтметра. Также нетрудно определить силу тока, протекающего между контактами. Для этого достаточно к схеме последовательно подключить амперметр. Получив эти два параметра, по закону Ома можно определить сопротивление схемы. Его называют входным. Иногда при этом рассматривают входное сопротивление длинной линии. Его определяющим свойством является то, что при подключении нагрузки к клеммам источника питания электрические характеристики не меняются.

Устройство блока может быть достаточно сложным, но в рассматриваемом случае не принимаются во внимание особенности его конструкции. Фактически можно представить, что внутри как бы находится резистор с определенным активным сопротивлением, соответствующим измеренному.

Входное электрическое сопротивление рассматривается как общая характеристика конкретного блока. Напряжение на вход может поступать с выхода другого блока или, например, с клемм аккумулятора или батареи.

Что такое внутреннее сопротивление при переменном токе

В предыдущем разделе было рассмотрено чисто активное сопротивление. При наличии в цепи только активного сопротивления фазы напряжения и тока совпадают. В реальных схемах обязательно присутствует реактивное сопротивление, которое делится еще на ёмкостное и индуктивное. Для постоянного тока его значение принято считать пренебрежимо малым и не принимать во внимание при расчёте параметров.

Если используется переменное напряжение на входе, тогда рассматривается полное сопротивление, состоящее из активного и реактивного. Их суммируют, используя правило прямоугольного треугольника. В этом случае один катет соответствует активному сопротивлению, второй — реактивному, а гипотенуза — полному или импедансу.

Важно учитывать, что в цепи с переменным током фаза напряжения сдвигается относительно фазы тока. Сдвиг фаз зависит от соотношения активного и реактивного сопротивлений конкретной цепи.

При отсутствии конденсаторов и катушек индуктивности в цепи емкостным и индуктивным сопротивлениями можно пренебречь и учитывать только активное. В этом случае ток будет следовать за напряжением, одновременно принимая нулевые и максимальные значения.

Если же в цепь включить катушку или конденсатор, создающих индуктивное или емкостное сопротивление настолько большого значения, что активное становится пренебрежимо малым, то сдвиг фаз будет равен π/2.

Так как реактивное сопротивление зависит от частоты поступающего сигнала, то чтобы более точно определить импеданс, необходимо узнать нужные параметры при двух различных частотах.

Следует принимать во внимание, что входное полное сопротивление линии может быть различным в отличающихся температурных условиях. Характер и величина отличий зависит от конкретного устройства рассматриваемого блока. Также требуется учитывать обратное влияние самой процедуры измерения на электрические параметры схемы.

Входное сопротивление зависит еще и от того, каким способом вводится в цепь сигнал обратной связи (ОС). Если этот сигнал отсутствует, то входное сопротивление определяется напряжением и током, присутствующими на входе. В том случае, когда обратную связь вводят по последовательной схеме, сопротивление на входе увеличивается при отрицательной ОС и уменьшается при положительной ОС.

При использовании параллельной схемы введения ОС входное сопротивление уменьшается и при отрицательной, и при положительной ОС. При небольшом сопротивлении в цепи ОС оно может составлять десятые, и даже тысячные доли Ома.

Как измерить

При определении входных параметров блока его устройство не рассматривается, но при этом может возникнуть необходимость провести измерение входного сопротивления. Блок выглядит как чёрный ящик, имеющий две входных и две выходных клеммы. Наиболее простым решением является определение входного напряжения и силы тока. Для простоты можно предположить, что рассматривается постоянный ток. Определить входное электрическое сопротивление в этом случае можно способом, который описан далее.

Найти входное сопротивление можно, разделив напряжение на силу тока. Однако в рассматриваемом случае нужно понимать, что если напряжение подаётся с батареи, то на показания будет влиять внутреннее сопротивление источника тока.

Если в блоке используется конденсатор, то нужно учитывать, что через него ток проходить не будет. С другой стороны, для переменного тока он помехой не является. Для переменного тока в качестве входного сопротивления цепи рассматривается полное сопротивление (импеданс). Оно представляет собой векторную сумму активного (омического) и реактивного (индуктивного и ёмкостного) сопротивлений. Однако его значение будет отличаться при различных частотах. Поэтому процедура измерения является более сложной по сравнению с постоянным током. В этом случае может быть использована следующая схема.

В данной схеме применён генератор переменного тока, который расположен слева. Его соединяют с исследуемым блоком, подавая на него переменный ток. На одном из соединительных проводов ставится резистор с известным сопротивлением R.

Напряжение измеряют дважды — перед резистором и после него. Пусть его значение будет равно U1 и U2 соответственно. Как известно, при переменном входном токе I(вх) падение напряжения на этой детали составит U2 – U1. С другой стороны оно будет равно I(вх) × R. В результате может быть получена следующая формула:

U2 − U1 = I(вх) × R.

Из этой формулы можно определить величину входного тока:

I(вх) = ( U2 − U1 ) / R.

На вход исследуемого блока поступает напряжение U2:

I(вх) = U2 / R(вх).

Входное сопротивление R(вх) найдем, используя формулу:

( U2 − U1 ) / R = U2 / R(вх).

Определяем значение сопротивления:

R(вх) = R × U2 / ( U2 − U1 ).

Все величины в правой части равенства являются известными или были измерены. Подставив их формулу, можно определить величину входного сопротивления схемы.

Применение описанного здесь способа позволяет точно вычислять входное сопротивление даже в тех случаях, когда оно очень велико.

Выходное напряжение

При рассмотрении упрощённой схемы блока видно, что у него имеется выходное напряжение. Оно появляется на контактах, указанных на изображении справа.

На рисунке показан идеальный источник тока, который, как предполагается, не имеет внутреннего сопротивления. Это означает, что может быть создан сколько угодно большой ток. Имеющийся на схеме резистор нарушает определенную идеальность, ограничивая величину тока при коротком замыкании.

Измерение выходного тока может быть выполнено следующим образом. Напряжение U является известной величиной. При коротком замыкании может быть измерен проходящий по контактам ток. Выходное сопротивление R(вых) определяется по закону Ома. Для его вычисления необходимо напряжение разделить на ток.

Однако этот способ неудобен, так как большой ток нарушает условия функционирования схемы и может привести к поломкам. Поэтому на практике между клеммами ставят дополнительный резистор с известной величиной сопротивления R и только после этого измеряют значение силы тока I и напряжения U2. Предварительно следует определить разность потенциалов U1 с помощью вольтметра. Исходя из закона Ома, получают следующую формулу:

R(вых) = ( U2 – U1 ) / ( U2 / R ).

Практическое применение

Понятие входного сопротивления играет важную роль при согласовании характеристик соединённых между собой блоков. Сказанное можно пояснить на следующем примере.

Предположим, что первым блоком является источник питания. Если к его клеммам присоединён следующий блок, то при практическом определении его входного сопротивления станет понятно, что оно немного меньше расчётной величины.

Это связано с наличием внутреннего сопротивления аккумулятора. Чем оно больше, тем искажение заметнее. Аналогичная ситуация наблюдается при соединении двух любых других блоков. Чтобы передача сопротивления проходила с минимальными потерями, необходимо, чтобы выходное сопротивление предыдущего блока было намного меньше входного у последующего.

С учетом этого обстоятельства необходимо уметь определять рассматриваемые величины, а при создании схемы обеспечивать их правильное соотношение. Если оно будет нарушено, то произойдёт значительное падение напряжения при передаче.

На практике обычно сталкиваются с очень большими значениями входных сопротивлений. В некоторых случаях они могут достигать 1 МОм. Это часто происходит при относительно небольшом входном напряжении. В результате сила рассматриваемого тока получается также небольшой.

В электронике входное и выходное сопротивление играют важную роль. Все качественные измерительные приборы стараются делать с очень высоким входным сопротивлением, чтобы оно минимально сказывалось на измеряемом сигнале и не гасило его амплитуду.

Что касается качественных источников питания, то их выпускают с очень небольшим выходным сопротивлением, чтобы при подключении низкоомной нагрузки напряжение на выходе «не проседало». Но даже если это случится, его можно подкорректировать вручную, используя регулировку выходного напряжения, присутствующую в каждом нормальном источнике питания.

Видео по теме

Источник

Понятно, что просто подключив омметр к усилителю, измерить выходное или входное сопротивление УНЧ или другого радиоустройства не получится. А как тогда это правильно сделать? Сейчас узнаете…

Метод измерения входного сопротивления

Из треугольника сопротивления переменного тока можно определить входное или выходное сопротивление двухконтактной сети путем измерения переменного тока и напряжения слабого сигнала.

Для входа напряжение измеряется на входных клеммах, а ток измеряется путем включения измерителя последовательно с генератором сигналов. Используйте фиксированную частоту, например 1 кГц, и установите уровень генератора примерно на 20 мВ RMS. Тогда если среднеквадратичное значение 20 мВ и ток 10 мкА, то сопротивление равно 2 кОм. В цепях с высоким сопротивлением ток становится очень маленьким и его трудно измерить, поэтому требуется альтернативный метод.

Простой способ измерения небольших входных токов — использование постоянного резистора как показано на схеме. Измерьте переменное напряжение в точках V1 и V2, тогда входной ток Iin станет:

Iin = (V2 – V1) / R1

Затем входное сопротивление тестируемой цепи находится по формуле:

Z = V1 / Iin

Пример. Если используем резистор 10 кОм для R1 и измеряем V2 = 10,1 мВ и V1 = 10 мВ, тогда:

Ток 10 нА было бы очень трудно измерить, так как разрешение цифрового вольтметра очень низкое, но возможно измерение значений 10 мВ и 10,1 мВ, что позволяет найти входное сопротивление: оно будет 10 мВ / 10 нА = 1 МОм.

Использование программы моделирования

Для измерения входного сопротивления в полном спектре частот используйте следующую схему:

Вход представляет собой источник постоянного тока, его значение установлено на 1 ампер. Поскольку источники тока в большинстве программ моделирования являются идеальными и имеют бесконечное выходное сопротивление, придется использовать параллельно резистор с большим сопротивлением, как показано, чтобы избежать ошибок моделирования. Поскольку V = I х Z и используется 1 ампер, как показано для источника тока, то V = 1 х Z или V = Z. Следовательно, измерение входного напряжения возвращает входное сопротивление. Ось Y на выходном графике может быть помечена соответствующим образом.

Измерение выходного сопротивления

Выходное сопротивление также может быть определено с использованием аналогичной методики. Используется резистор с фиксированной нагрузкой, и выходное напряжение измеряется сначала при полной нагрузке, а затем без нагрузки.

На приведенной выше схеме Zo — это внутреннее выходное сопротивление измеряемой сети. Термин «сеть» является общим термином, так как схема может быть чем угодно: усилителем, фильтром, генератором и так далее.

Чтобы найти выходное сопротивление, сначала измеряется выходное напряжение без нагрузочного резистора, а затем с фиксированной нагрузкой (чисто резистивной).

Сначала снимается нагрузочный резистор Rl, измеряется и записывается выходное напряжение (В). Затем Rl снова включается в цепь и напряжение на выходе под нагрузкой (Vl). Выходное сопротивление Zo теперь находится по закону Ома для цепей переменного тока. Поскольку нагрузка является чисто резистивной, Z = V / I, где «V» — падение напряжения на выходном сопротивлении: (V — Vl), а «I» — выходной ток, Vl / Rl. Таким образом:

Делаем перестановку:

Использование программы моделирования

Для измерения входного сопротивления по полному спектру частот используйте следующую схему:

Вход представляет собой источник постоянного тока, его значение установлено на 1 ампер. Поскольку источники тока в большинстве программ моделирования являются идеальными и имеют бесконечное выходное сопротивление, придется использовать параллельно резистор с большим сопротивлением, чтобы избежать ошибок моделирования. Поскольку V = I х Z и используется 1 ампер, как показано для источника тока, то V = 1 х Z или V = Z. Следовательно измерение выходного напряжения возвращает выходное сопротивление.

Источник

Можно
рассчитать входное сопротивление линии
в точке с координатой «y» по измеренным
значениям сопротивлений холостого хода
и короткого замыкания. Разделив числитель
и знаменатель (5.1) на
получим:

(5.4)

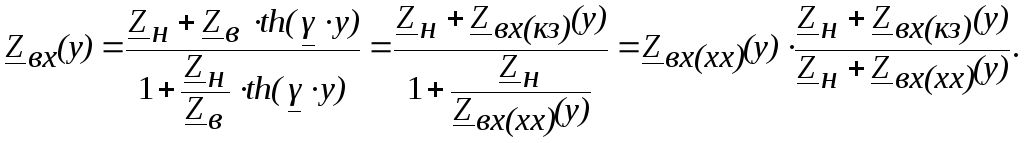
5.2. Определение вторичных параметров.

Определить
вторичные параметры (волновое сопротивление
и постоянную распространения) однородной
линии можно по результатам измерений
входного сопротивления в режиме короткого
замыкания и в режиме холостого хода.

Из анализа выражений
(5.2) и (5.3) следует, что волновое сопротивление
может быть определено

. (5.5)

Для
определения постоянной распространения
рассмотрим выражение, получаемое при
делении: ,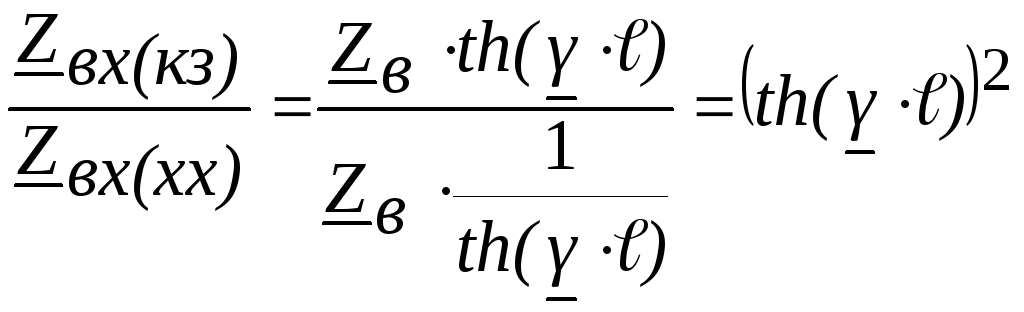
откуда

. (5.6)

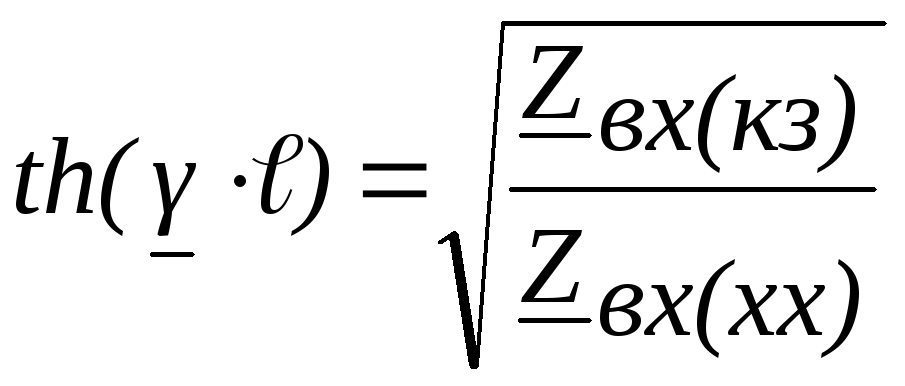
Выполним
преобразование ,
тогда .
Решим полученное уравнение относительно
,
представив результат в показательной
форме: .

Если
,
тогда ;
.

Учитывая,
что
,
коэффициент ослабления и коэффициент
фазы:

, (5.7)

,
(5.8)

где
k
– целое число длин волн λ, укладывающихся
вдоль линии .

5.3. Определение первичных параметров.

Обратимся к формулам
(2.6) и (2.8):

Перемножив
эти формулы, получим:
,
где–
реальная часть произведения; –
мнимая часть произведения (зная частоту,
можно определить L₀).

Разделив
эти формулы, получим:
,
где–
реальная часть частного; –
мнимая часть частного (зная ω, можно
определить С₀).

6. Линия без искажений.

Для
передачи сигнала по линии без искажений
необходимо, чтобы для каждой составляющей
спектра входного сигнала ослабление
и фазовая скорость были бы постоянными:

(6.1)

,
или
. (6.2)

Рассмотрим
выражение, определяющее коэффициент
распространения:

Если

,
(6.3)

тогда

То
есть при выполнении условия (6.3), называемом
условием Хевисайда, выполняются равенства
(6.1) и (6.2) и передача сигнала по линии
происходит без искажений.

7. Линия без потерь.

Если
первичные параметры линии
,
то она называется линией без потерь
(рис. 4). Такая идеализация справедлива
для коротких по длине линий, работающих
на сверхвысоких частотах (фидеров,
элементов р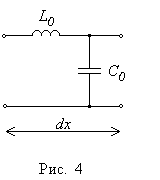адиотехнических
устройств, полосковых линий, согласующих
СВЧ устройств и других), где выполняются
условияи,
и резистивными сопротивлением и
проводимостью можно пренебречь по
сравнению с сопротивлением индуктивности
и проводимостью ёмкости в линии.

Коэффициент
распространения линии без потерь:

и
условия (6.1), (6.2) выполняются: коэффициент
ослабления амплитуды
а коэффициент фазылинейно зависит от частоты, при этом
фазовая скоростьравна постоянной величинеЛиния без потерь не вносит амплитудно-частотных
и фазочастотных искажений в передаваемый
сигнал.

Волновое
сопротивление линии без потерь
является резистивным.

Уравнения
передачи (2.10 б) для линии без потерь с
учётом
ипринимают вид:

(7.1)

(7.2)

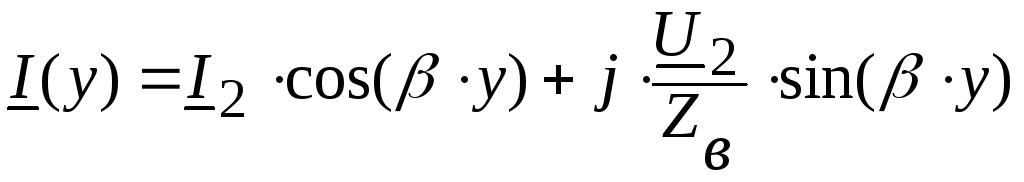
Входное
сопротивление линии без потерь, согласно
(5.1),

(7.3)

С
учётом

(7.4)

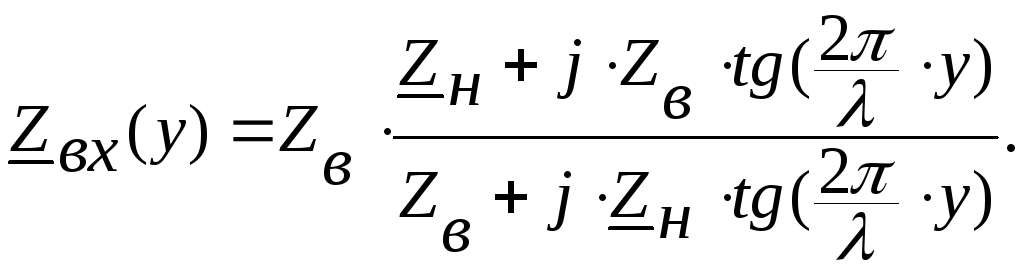
В
зависимости от нагрузки
на конце линии различают следующие
режимы работы:

–
линия с разомкнутыми выходными зажимами
,

–
линия с замкнутыми накоротко выходными
зажимами
,

–
подключение к линии реактивной нагрузки
,

–
подключение к линии согласованной
нагрузки
,

–
подключение к линии несогласованной
нагрузки
.

Рассмотрим
распределение напряжения и тока вдоль
линии при различных режимах работы.
Уравнения передачи линии без потерь
(7.1), (7.2) с учётом
имеют вид:

(7.5)

,
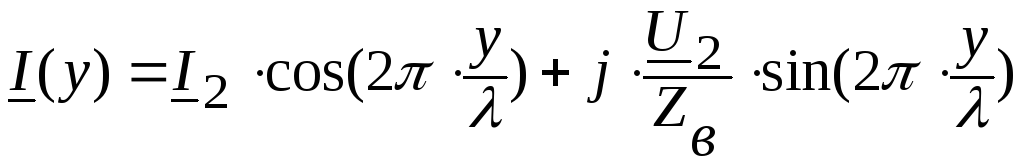
(7.6)

где
,– комплексные значения напряжения и
тока в конце линии (то есть в нагрузке);,– комплексные значения напряжения и
тока на расстоянииу
от конца линии.

7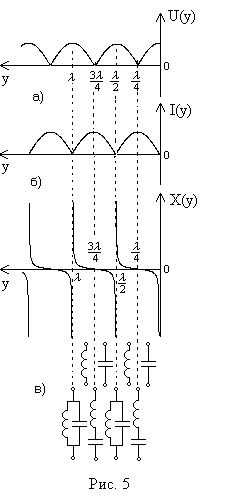.1.
В режиме холостого хода,
то есть когда линия на конце разомкнута
,уравнения (7.5), (7.6) преобразуются в:

(7.7)

.
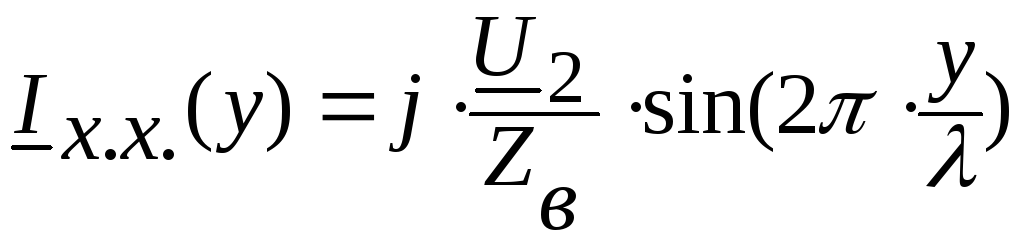
(7.8)

Если
начальную фазу напряжения
принять равной нулю (,),
тогда мгновенные значения напряжения
и тока:

(7.9)

(7.10)

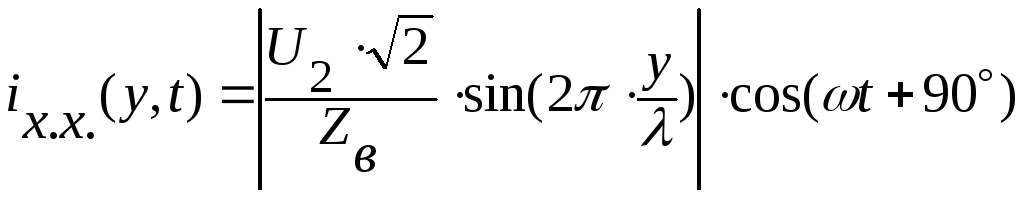
Действующие
значения напряжения и тока в
раз меньше амплитудных и соответственно
определяются из выражений:

(7.11)

(7.12)

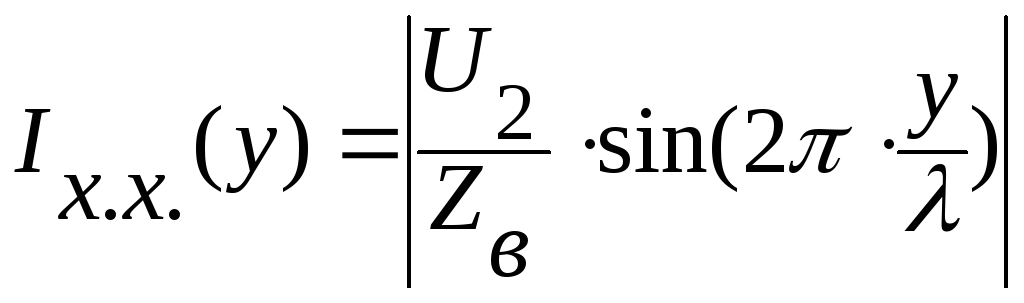
В
выражения (7.11), (7.12) переменная времени
не входит, следовательно, распределение
действующих значений напряжения и тока
вдоль линии с течением времени не
меняется. Рассмотренный режим колебаний
называют режимом
стоячих волн.

На
рисунках 5.а и 5.б показано распределение
действующих значений напряжения и тока
вдоль линии. В линии имеются точки, где
амплитуда колебаний равна нулю (узлы
напряжения или тока) и точки, где амплитуда
колебаний максимальна (пучности
напряжения или тока). Стоячие волны
являются результатом сложения падающей
и отражённой волн с равными амплитудами
().
В пучностях фазы обеих волн совпадают
и амплитуда суммарной волны вдвое больше
амплитуды падающей волны, а в узлах фазы
противоположны и амплитуда суммарной
волны равна нулю.

Условия возникновения
стоячей волны могут быть сформулированы
так:

1. α = 0 дБ/м – линия
без потерь;

2.
|n2|
= 1, или Р_н
= U₂·I₂·cos(φ_z)
= 0 – полное
отражение падающей волны от выходных
зажимов линии.

При
этом U(y)
и I(y)
– распределения вдоль линии значений
амплитуд колебаний, – определяются
законами синус или косинус; а фазы этих
колебаний от координаты «у» не зависят.

Входное
сопротивление разомкнутой линии в
режиме холостого хода на расстоянии
«у»
от выходных зажимов:

(7.13)

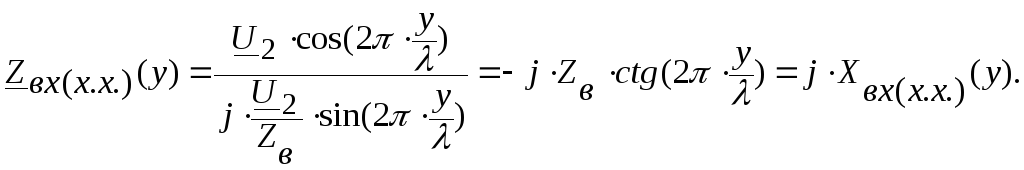
График
зависимости Х_вх(х.х.)(у)
представлен на рисунке 5.в.

Разомкнутая
на конце линия длиной от 0 до
имеет входное сопротивлениеемкостного
характера
(Х_вх(х.х.)< 0).

Линия
длиной
имеет входное сопротивление равное 0,
то есть такой отрезок длинной линии
аналогиченпоследовательному
колебательному контуру
без потерь (Х_вх(х.х.)= 0).

Линия
длиной от
доимеет входное сопротивлениеиндуктивного
характера
(Х_вх(х.х.)> 0).

Линия
длиной
имеет неограниченно большое входное
сопротивление (Х_вх(х.х.)= ∞ ), то есть такой
отрезок длинной линии аналогичен
параллельному
колебательному контуру
без потерь.

7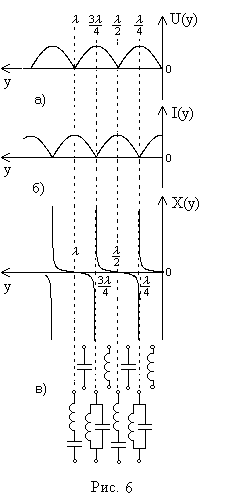.2.
В режиме короткого замыкания,
то есть когда линия на конце замкнута
,уравнения (7.1), (7.2), (7.3) преобразуются:

(7.14)

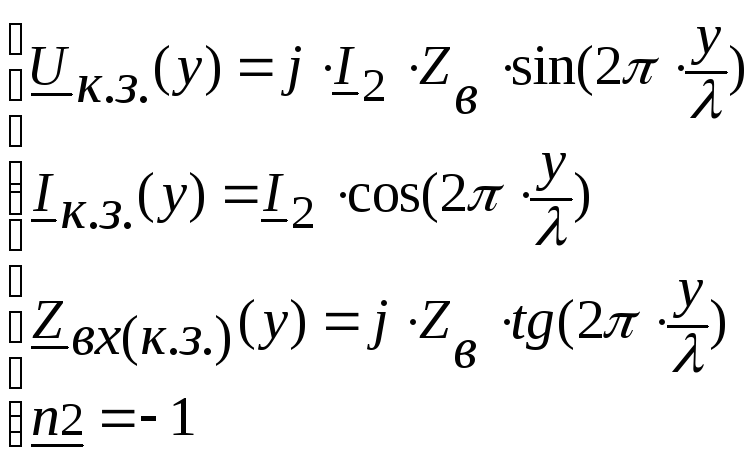
Если
начальную фазу тока I₂
принять равной нулю, тогда мгновенные
значения напряжения и тока:

(7.15)

Графики
распределения амплитудных значений
напряжения и тока, а также и входного
сопротивления, вдоль линии показаны на
рисунках 6.(а, б, в). В короткозамкнутой
линии, также как и в разомкнутой, имеет
место режим стоячих волн.

Короткозамкнутая
линия без потерь длиной
имеет неограниченно большое входное
сопротивление (X_вх(к.з.)=
∞). Если в линии имеются потери, то
входное сопротивление не бесконечно,
но достаточно велико. Это свойство
используется в схемотехнике.

7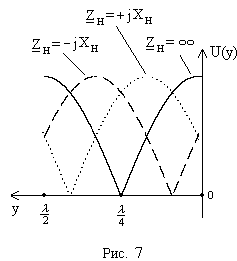.3.
При нагрузке линии на реактивное
сопротивление
образуются стоячие волны, как и в режимах
холостого хода и короткого замыкания.
Коэффициент отражения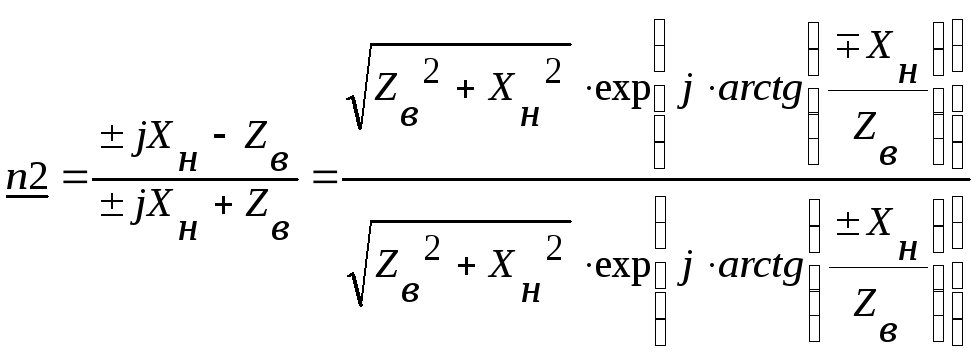,|n2|=1.
То есть в этом режиме работы длинной
линии так же происходит сложение падающей
и отражённой волн с равными амплитудами.

Реактивный
элемент, подключаемый к линии в качестве
нагрузки, можно заменить эквивалентным
отрезком линии, входное сопротивление
которого равно сопротивлению реактивного
элемента. Емкостной элемент можно
заменить разомкнутым отрезком линии
длиной
,
а индуктивный элемент – короткозамкнутым
отрезком длиной.

Если
нагрузка индуктивная, узлы и пучности
сдвигаются влево, в сторону генератора,
и вправо, в сторону нагрузки, если она
емкостная (рис. 7).

7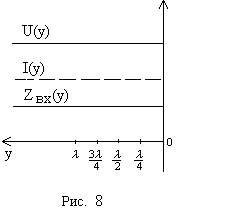.4.
Если линия нагружена на резистивное
сопротивление, равное волновому
,
то нагрузка является согласованной. В
этом случае комплексные действующие
значения напряжения и тока на выходных
зажимах линии связаны соотношением:.

Напряжение
и ток совпадают по фазе, так как в линии
без потерь Z_в
принимает действительное (не комплексное)
значение. Коэффициент отражения n2=0,
и в линии существует только падающая
волна с неизменной амплитудой (рисунок
8).

Если
начальную фазу напряжения
принять равной нулю (,),
то

,
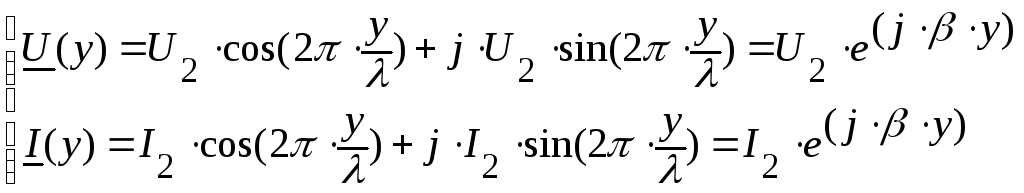
(7.16)

тогда мгновенные
значения напряжения и тока:

.
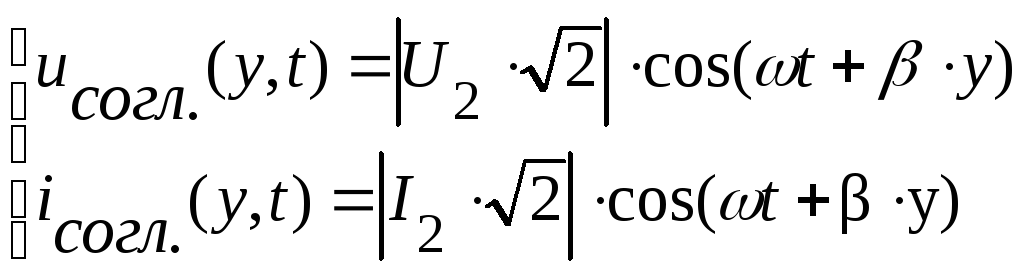
(7.17)

В
линии без потерь при согласованной
нагрузке образуется бегущая
волна,
амплитуда которой не зависит от
расстояния, а фаза – зависит.

Входное
сопротивление согласованной линии
резистивное, равно волновому сопротивлению
и не зависит от длины линии.

7.5.
При подключении несогласованной
резистивной нагрузки
действующие значения напряжения и тока
на выходных зажимах линии связаны
соотношением:,
тогда

Введём
параметр: .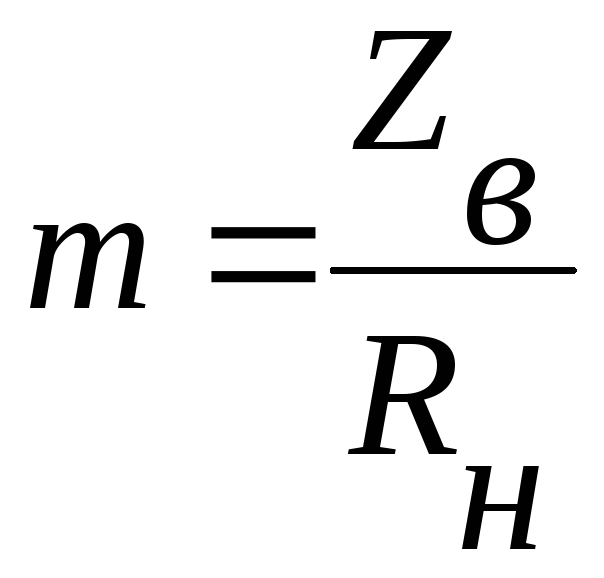
Коэффициент отражения |n2|<1.
В линии одновременно присутствуют как
бегущие, так и стоячие волны. Это можно
показать на примере выражения:

В
получившемся выражении первое слагаемое
представляет собой бегущую волну
(амплитуда не зависит от расстояния;
фаза – зависит), а второе слагаемое
представляет собой стоячую волну
(амплитуда зависит от расстояния по
закону cos(βy);
фаза – не зависит).

Следовательно,
в линии без потерь при резистивной
несогласованной нагрузке существует
режим смешанных
волн.

Распределение
действующего значение напряжения вдоль
линии описывается выражением:

. (7.18)

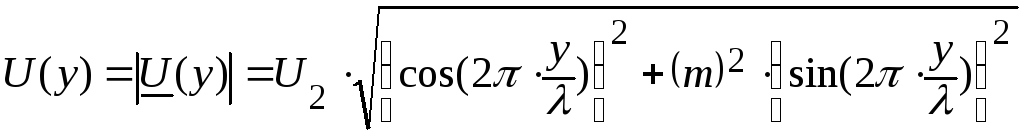
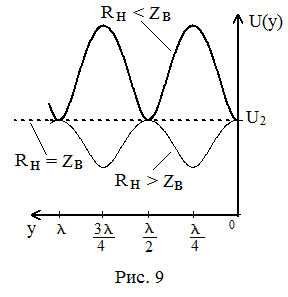
Графики
распределения действующих значений
напряжения вдоль линии при различных
соотношениях между R_н
и Z_в
приведены на рисунке 9.

Чем
больше отличие между значениями
сопротивления нагрузки R_н
и волновым сопротивлением Z_в,
тем больше отличие между максимальным
и минимальным значениями напряжения
U_max
и U_min.
Для количественной оценки этого отличия,
то есть степени рассогласования линии
с нагрузкой, служит коэффициент
бегущей волны:

(7.19)

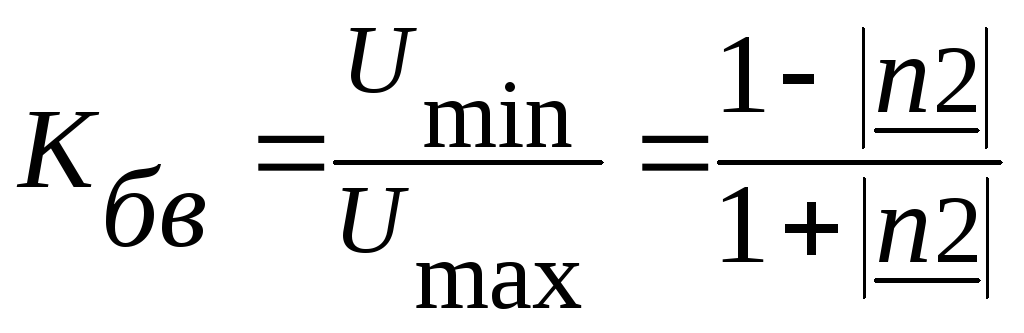
В
ряде случаев используют понятие
коэффициента
стоячей волны:

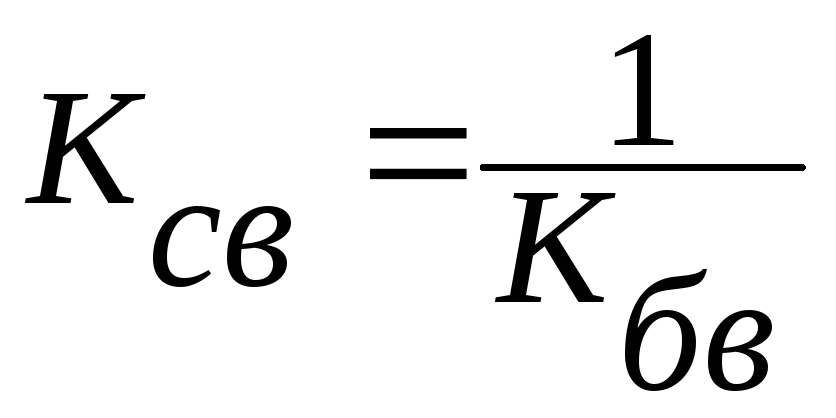
Соседние файлы в предмете Теория электрических цепей

Источник

From Wikipedia, the free encyclopedia

The input impedance of an electrical network is the measure of the opposition to current (impedance), both static (resistance) and dynamic (reactance), into the load that is external to the electrical source network. The input admittance (the reciprocal of impedance) is a measure of the load network’s propensity to draw current. The source network is the portion of the network that transmits power, and the load network is the portion of the network that consumes power.

The circuit to the left of the central set of open circles models the source circuit, while the circuit to the right models the connected circuit. Z_S is the output impedance seen by the load, and Z_L is the input impedance seen by the source.

Input impedance[edit]

If the load network were replaced by a device with an output impedance equal to the input impedance of the load network (equivalent circuit), the characteristics of the source-load network would be the same from the perspective of the connection point. So, the voltage across and the current through the input terminals would be identical to the chosen load network.

Therefore, the input impedance of the load and the output impedance of the source determine how the source current and voltage change.

The Thévenin’s equivalent circuit of the electrical network uses the concept of input impedance to determine the impedance of the equivalent circuit.

Calculation[edit]

If one were to create a circuit with equivalent properties across the input terminals by placing the input impedance across the load of the circuit and the output impedance in series with the signal source, Ohm’s law could be used to calculate the transfer function.

Electrical efficiency[edit]

The values of the input and output impedance are often used to evaluate the electrical efficiency of networks by breaking them up into multiple stages and evaluating the efficiency of the interaction between each stage independently. To minimize electrical losses, the output impedance of the signal should be insignificant in comparison to the input impedance of the network being connected, as the gain is equivalent to the ratio of the input impedance to the total impedance (input impedance + output impedance). In this case,

${displaystyle Z_{in}gg Z_{out}}$

(or ${displaystyle Z_{L}gg Z_{S}}$

)

The input impedance of the driven stage (load) is much larger than the output impedance of the drive stage (source).

Power factor[edit]

In AC circuits carrying power, the losses of energy in conductors due to the reactive component of the impedance can be significant. These losses manifest themselves in a phenomenon called phase imbalance, where the current is out of phase (lagging behind or ahead) with the voltage. Therefore, the product of the current and the voltage is less than what it would be if the current and voltage were in phase. With DC sources, reactive circuits have no impact, therefore power factor correction is not necessary.

For a circuit to be modelled with an ideal source, output impedance, and input impedance; the circuit’s input reactance can be sized to be the negative of the output reactance at the source. In this scenario, the reactive component of the input impedance cancels the reactive component of the output impedance at the source. The resulting equivalent circuit is purely resistive in nature, and there are no losses due to phase imbalance in the source or the load.

${displaystyle {begin{aligned}Z_{in}&=X-joperatorname {Im} (Z_{out})\end{aligned}}}$

Power transfer[edit]

The condition of maximum power transfer states that for a given source maximum power will be transferred when the resistance of the source is equal to the resistance of the load and the power factor is corrected by canceling out the reactance. When this occurs the circuit is said to be complex conjugate matched to the signals impedance. Note this only maximizes the power transfer, not the efficiency of the circuit. When the power transfer is optimized the circuit only runs at 50% efficiency.

The formula for complex conjugate matched is

${displaystyle {begin{aligned}Z_{in}&=Z_{out}^{*}\&=leftvert Z_{out}rightvert e^{-jTheta _{out}}\&=operatorname {Re} (Z_{out})-joperatorname {Im} (Z_{out}).\end{aligned}}}$

When there is no reactive component this equation simplifies to $Z_{{in}}=Z_{{out}}$ as the imaginary part of $Z_{out}$ is zero.

Impedance matching[edit]

When the characteristic impedance of a transmission line, ${displaystyle Z_{line}}$ , does not match the impedance of the load network, ${displaystyle Z_{in}}$ , the load network will reflect back some of the source signal. This can create standing waves on the transmission line. To minimize reflections, the characteristic impedance of the transmission line and the impedance of the load circuit have to be equal (or “matched”). If the impedance matches, the connection is known as a matched connection, and the process of correcting an impedance mismatch is called impedance matching. Since the characteristic impedance for a homogeneous transmission line is based on geometry alone and is therefore constant, and the load impedance can be measured independently, the matching condition holds regardless of the placement of the load (before or after the transmission line).

$Z_{{in}}=Z_{{line}}$

Applications[edit]

Signal processing[edit]

In modern signal processing, devices, such as operational amplifiers, are designed to have an input impedance several orders of magnitude higher than the output impedance of the source device connected to that input. This is called impedance bridging. The losses due to input impedance (loss) in these circuits will be minimized, and the voltage at the input of the amplifier will be close to voltage as if the amplifier circuit was not connected. When a device whose input impedance could cause significant degradation of the signal is used, often a device with a high input impedance and a low output impedance is used to minimize its effects. Voltage follower or impedance-matching transformers are often used for these effects.

The input impedance for high-impedance amplifiers (such as vacuum tubes, field effect transistor amplifiers and op-amps) is often specified as a resistance in parallel with a capacitance (e.g., 2.2 MΩ ∥ 1 pF). Pre-amplifiers designed for high input impedance may have a slightly higher effective noise voltage at the input (while providing a low effective noise current), and so slightly more noisy than an amplifier designed for a specific low-impedance source, but in general a relatively low-impedance source configuration will be more resistant to noise (particularly mains hum).

Radio frequency power systems[edit]

Signal reflections caused by an impedance mismatch at the end of a transmission line can result in distortion and potential damage to the driving circuitry.

In analog video circuits, impedance mismatch can cause “ghosting”, where the time-delayed echo of the principal image appears as a weak and displaced image (typically to the right of the principal image). In high-speed digital systems, such as HD video, reflections result in interference and potentially corrupt signal.

The standing waves created by the mismatch are periodic regions of higher than normal voltage. If this voltage exceeds the dielectric breakdown strength of the insulating material of the line then an arc will occur. This in turn can cause a reactive pulse of high voltage that can destroy the transmitter’s final output stage.

In RF systems, typical values for line and termination impedance are 50 Ω and 75 Ω.

To maximise power transmission^{[clarification needed]} for radio frequency power systems the circuits should be complex conjugate matched throughout the power chain, from the transmitter output, through the transmission line (a balanced pair, a coaxial cable, or a waveguide), to the antenna system, which consists of an impedance matching device and the radiating element(s).

References[edit]

The Art of Electronics, Winfield Hill, Paul Horowitz, Cambridge University Press, ISBN 0-521-37095-7
“Aortic input impedance in normal man: relationship to pressure wave forms”, JP Murgo, N Westerhof, JP Giolma, SA Altobelli pdf
An excellent introduction to the importance of impedance and impedance matching can be found in A practical introduction to electronic circuits, M H Jones, Cambridge University Press, ISBN 0-521-31312-0

External links[edit]

Calculation of the damping factor and the damping of impedance bridging
Interconnection of two audio units – Input impedance and output impedance
Impedance and Reactance
Input Impedance Measurement

Источник

Предисловие

Входное сопротивление

Как измерить входное сопротивление

Измерение входного сопротивления на практике

Выходное сопротивление

Измерение выходного сопротивления на практике

Заключение

Что такое входное сопротивление и как его измерить

Понятие входного сопротивления для постоянного тока

Что такое внутреннее сопротивление при переменном токе

Как измерить

Выходное напряжение

Практическое применение

Видео по теме

Метод измерения входного сопротивления

Использование программы моделирования

Измерение выходного сопротивления

Использование программы моделирования

5.2. Определение вторичных параметров.

5.3. Определение первичных параметров.

6. Линия без искажений.

7. Линия без потерь.

Input impedance[edit]