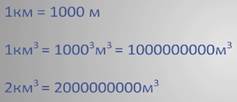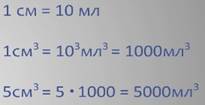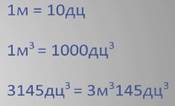Содержание:
- § 1 Формула объема куба
- § 2 Перевод кубических метров в кубические дециметры, сантиметры миллиметры, литры и наоборот
§ 1 Формула объема куба
В этом уроке Вы познакомитесь с формулой объема куба, научитесь переводить кубические метры в кубические дециметры, сантиметры, миллиметры, литры и наоборот.
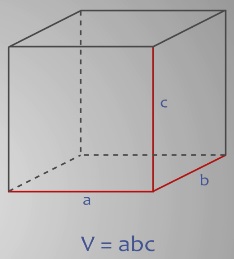
Объем прямоугольного параллелепипеда вычисляется по формуле V =abc, где a, b и с – его измерения: длина, ширина и высота.
А что, если все три измерения в прямоугольном параллелепипеде равны?
Тогда он является кубом.
Значит, чтобы найти объем куба, необходимо также перемножить три его измерения, но поскольку все они равны, то достаточно просто ребро куба возвести в куб.
Т.е. объем куба V равен а умножить на а умножить на а и равно а в кубе, где а – это длина ребра куба.
Давайте выполним следующее задание:
Найдите объем куба со стороной 6 см.
Решение:
Подставим вместо а длину стороны 6 см.
Ответ: объем куба равен 216 кубическим сантиметрам.
§ 2 Перевод кубических метров в кубические дециметры, сантиметры миллиметры, литры и наоборот
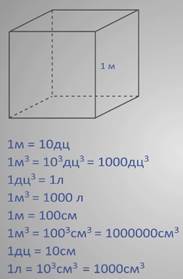
Давайте рассмотрим куб с ребром один метр. Его объем составляет один кубический метр.
А как можно выразить его объем, к примеру, в сантиметрах или дециметрах?
Очень просто!
Так как в одном метре 10 дециметров, значит в одном кубическом метре 10 в кубе кубических дециметров, т.е. 1000 кубических дециметров.
Следует вспомнить, что один кубический дециметр равен одному литру, значит один кубический метр составляет 1000 литров.
Так же можно выразить кубический метр в сантиметрах, поскольку в одном метре 100 сантиметров, значит в одном кубическом метре 100 в кубе кубических сантиметров, или миллион кубических сантиметров.
Таким же образом можем найти сколько кубических сантиметров содержится в одном литре. Так как один литр равен одному кубическому дециметру, и в одном дециметре десять сантиметров, значит в одном литре десять в кубе кубических сантиметров, т.е. тысяча кубических сантиметров.
Давайте выполним несколько заданий.
Задание первое: выразите 2 кубических километра в кубических метрах.
Решение: в 1 километре 1000 метров, значит в 1 кубическом километре 1000 в кубе кубических метров, т.е. 1 миллиард кубических метров.
Значит 2 кубических километра содержат 2 миллиарда кубических метров.
Задание второе: выразите 5 кубических сантиметров в кубических миллиметрах.
Решение: так как в одном сантиметре содержится 10 миллиметров, значит в одном кубическом сантиметре содержится 10 в кубе кубических миллиметров, т.е. тысяча кубических миллиметров.
Получаем, что пять кубических сантиметров равно 5 умножить на 1000 равно 5 000 кубических миллиметров.
И последнее задание: выразите 3 145 кубических дециметров в кубических метрах и дециметрах.
Решение: так как в 1 метре 10 дециметров, значит в 1 кубическом метре 1000 кубических дециметров. Следовательно, 3 тысячи 145 кубических дециметров равно 3 кубическим метрам и 145
кубическим дециметрам.
Таким образом, в этом уроке Вы познакомились с формулой объема куба и научились переводить кубические метры в кубические дециметры, сантиметры, миллиметры а также литры и наоборот.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
Мы больше не будем рекомендовать вам подобный контент.
Отмена
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3
2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.
Следовательно, вычислить объем куба можно так:
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Напомним,
что призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Стороны
параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами
параллелепипеда. Две грани параллелепипеда называются противолежащими,
если они не имеют общего ребра.
Например,
грани и
–
противолежащие.
Грани,
имеющие общее ребро, называются смежными. Например, грани и
–
смежные, ребро у
них общее.
Иногда
какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями,
тогда остальные грани – боковыми гранями, а их стороны, соединяющие
вершины оснований параллелепипеда, – его боковыми рёбрами.
В
нашем случае у параллелепипеда грани
и
–
его основания. Остальные же грани являются боковыми гранями.
Две
вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
Отрезок, соединяющий, противолежащие вершины, называется диагональю
параллелепипеда. У параллелепипеда всего четыре диагонали.
Объединение
боковых граней называется боковой поверхностью параллелепипеда, а
объединение всех граней называется полной поверхностью параллелепипеда.
Тогда площадью боковой поверхности параллелепипеда называется сумма
площадей его боковых граней.
А
площадью полной поверхности параллелепипеда называется сумма площадей
всех его граней.
Параллелепипед
обладает следующими свойствами:
1.
Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам.
3.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его
измерений.
Объём
параллелепипеда равен произведению площади основания на
высоту.
Объём
прямоугольного параллелепипеда равен произведению трёх
его измерений.
Куб
– это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани
которого – равные квадраты.
Диагональ
куба с ребром равна
.
Объём
куба
равен ,
где –
ребро куба.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. В основании прямого параллелепипеда лежит параллелограмм
с основаниями см
и см
и острым углом .
Боковое ребро параллелепипеда равно см.
Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
вторая. Все грани параллелепипеда – ромбы с диагоналями см
и см.
Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
третья. Найдите меньшую диагональ прямого параллелепипеда
высотой см
со сторонами основания см
и см
и углом между ними .
Решение.
Задача
четвёртая. В прямоугольном параллелепипеде ребро
см,
см.
Найдите расстояние между диагональю параллелепипеда и
ребром .
Решение.
Задача
пятая. Две стороны основания параллелепипеда равны см
и см,
угол между ними .
Боковое ребро равно см
и наклонено к основанию под углом .
Найдите объём параллелепипеда.
Решение.
Задача
шестая. Все грани параллелепипеда – ромбы с периметром
равным и
острым углом .
Найдите объём параллелепипеда.
В ответ запишите значение .
Решение.
Как найти объем треугольной призмы и куба, формула
В этом видео рассказывается о том, как найти объем треугольной призмы и куба. Начинается урок с решения задачи по стереометрии, в которой требуется найти объем треугольной призмы, если известна длина основания треугольника и его высота, а также длина боковой стороны призмы. Решение данной задачи выполняется по формуле нахождения объёма прямоугольной призмы. Он равен произведению площади основания призмы на её высоту. Основанием призмы является треугольник и нам известна его высота и длина основания. Формула нахождения площади треугольника также известна. Она равна половине основания треугольника, умноженного на высоту. Для нахождения объема самой призмы остается только умножить полученный результат на длину боковой части призмы, т.е. её высоту. Во второй части урока решается задача на нахождение объема куба, если известна длина его стороны. Как известно, у куба все стороны равны, и объем куба вычисляется по простой формуле. Он равен длине стороны куба возведенной в третью степень Видео урок «Как найти объем треугольной призмы и куба, формула» вы можете смотреть онлайн абсолютно бесплатно в любое удобное время. Успехов!
- Длительность: 3:51
- Рейтинг: 0.0/0
- 1
- 2
- 3
- 4
- 5
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.